利用MATLAB绘制二维函数图形
- 格式:doc
- 大小:309.00 KB
- 文档页数:12




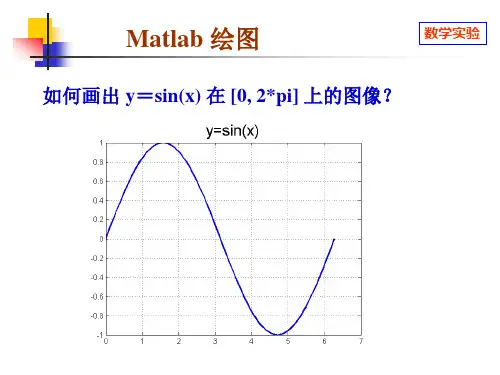

Matlab⼆维绘图函数(plot类)plot功能绘制⼆维图形的最基本函数。
语法//x为向量时,以x的元素值为纵坐标,x的序号为横坐标绘制曲线。
//x为矩阵时,以其序号为横坐标,按列绘制每列元素值相对于其序号的曲线。
polt(x)//以x 元素为横坐标值,y 元素为纵坐标值绘制曲线plot(x,y)//以公共的x 元素为横坐标值,以y1,y2,… 元素为纵坐标值绘制多条曲线plot(x,y1,x,y2,…)其他属性参数:符号作⽤符号作⽤符号作⽤符号作⽤y黄-实线.点<⼩于号m紫:点线o圆s正⽅形c青-.点划线x叉号d菱形r红⾊–虚线+加号h六⾓星g绿*星号p五⾓星b蓝v向下三⾓形w⽩^向上三⾓形k⿊>⼤于号egclear;clc;clf;x = linspace(0,2*pi,50);y = sin(x);plot(x,y)xlabel('x轴')ylabel('y轴')title('题⽬')gtext('正弦曲线') %图形上出现⼗字线,⿏标控制其移动,单击⿏标显⽰⽂字ezplot功能⽆需数据准备,直接画出函数图形语法//在默认区间[-2pi,2pi]上绘制函数f=f(x)ezplot(f)//在区间min < x < max上绘制函数 f = f(x)ezplot(f,[min,max])//对于隐式定义的函数f = f(x,y):ezplot(f)绘制的是 f(x,y) = 0ezplot(f,[xmin,xmax,ymin,ymax])//绘制含参函数 x = x(t)和y = y(t) 默认区间: 0 < t < 2pi.ezplot(x,y)//绘制含参函数 x = x(t)和y = y(t) 区间:tmin < t < tmax.ezplot(x,y,[tmin,tmax])//在指定的区域,在figure窗⼝绘制通过handle figure指定的函数ezplot(...,figure_handle)fplot功能通过MATLAB平台内部设置的⾃适应来动态决定⾃变量的离散间隔,当函数值变化缓慢时离散间隔取⼤些,当函数值变化剧烈时,离散间隔取⼩⼀些。
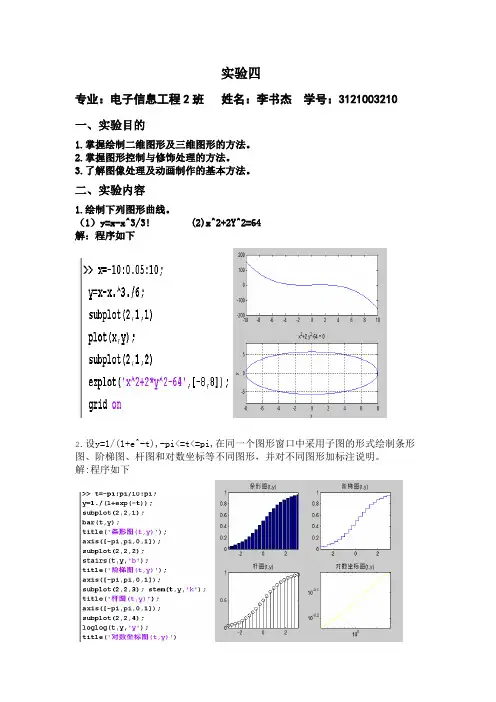
实验四
专业:电子信息工程2班姓名:李书杰学号:3121003210
一、实验目的
1.掌握绘制二维图形及三维图形的方法。
2.掌握图形控制与修饰处理的方法。
3.了解图像处理及动画制作的基本方法。
二、实验内容
1.绘制下列图形曲线。
(1)y=x-x^3/3! (2)x^2+2Y^2=64
解:程序如下
2.设y=1/(1+e^-t),-pi<=t<=pi,在同一个图形窗口中采用子图的形式绘制条形图、阶梯图、杆图和对数坐标等不同图形,并对不同图形加标注说明。
解:程序如下
3.绘制下列极坐标图。
(1)ρ=5cosθ+4 (2)γ=5sin^2φ/cosφ,-π/3<φ<π/3 解:程序如下
思考练习:
2.绘制下列曲线
(1)y=1/2πe^(-x^2/2) (2)x=tsint y=tcost
解:程序如下
(1)
结果如下:
(2)
结果如下:
3.在同一坐标中绘制下列两条曲线并标注两曲线交叉点。
(1)y=2x-0.5
(2)x=sin(3t)cost
Y=sin(3t)sint
解:程序如下
4.分别用plot和fplot函数绘制y=sin(1/x)的曲线,分析两曲线的差别。
解:程序如下
结果如下:
5.绘制下列极坐标图:
(1)p=12/sqrt(θ) (2)γ=3asinφcosφ/(sin^3φ+cos^3φ)解:程序如下
结果如下:。

matlab二维图形的绘制(2006-11-20 20:38:35)转载▼分类:matlab基础(电子方向)常用的二维图形命令:plot:绘制二维图形loglog:用全对数坐标绘图semilogx:用半对数坐标(X)绘图semilogy:用半对数坐标(Y)绘图fill:绘制二维多边填充图形polar:绘极坐标图bar:画条形图stem:画离散序列数据图stairs:画阶梯图errorbar:画误差条形图hist:画直方图fplot:画函数图title:为图形加标题xlabel:在X轴下做文本标记ylabel:在Y轴下做文本标记zlabel:在Z轴下做文本标记text:文本注释grid:对二维三维图形加格栅绘制单根二维曲线plot函数,基本调用格式为:plot(x,y)其中x和y为长度相同的向量,分别用于存储x坐标和y坐标数据。
例如:在区间内,绘制曲线y=2e-0.5xcos(4πx)程序如下:x=0:pi/100:2*pi;y=2*exp(-0.5*x).*cos(4*pi*x);plot(x,y)plot函数最简单的调用格式是只包含一个输入参数:plot(x)在这种情况下,当x是实向量时,以该向量元素的下标为横坐标,元素值为纵坐标画出一条连续曲线,这实际上是绘制折线图。
p=[22,60,88,95,56,23,9,10,14,81,56,23];plot(p)绘制多根二维曲线1.plot函数的输入参数是矩阵形式(1) 当x是向量,y是有一维与x同维的矩阵时,则绘制出多根不同颜色的曲线。
曲线条数等于y矩阵的另一维数,x被作为这些曲线共同的横坐标。
(2) 当x,y是同维矩阵时,则以x,y对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
(3) 对只包含一个输入参数的plot函数,当输入参数是实矩阵时,则按列绘制每列元素值相对其下标的曲线,曲线条数等于输入参数矩阵的列数。
当输入参数是复数矩阵时,则按列分别以元素实部和虚部为横、纵坐标绘制多条曲线。
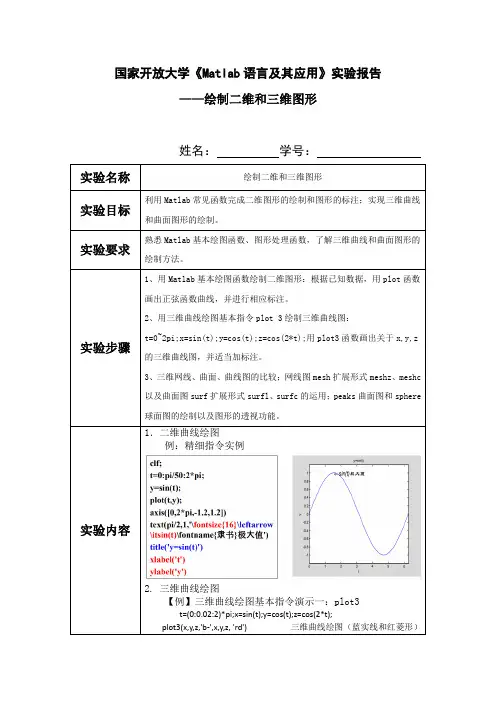


强大的绘图功能是Matlab的特点之一,Matlab提供了一系列的绘图函数,用户不需要过多的考虑绘图的细节,只需要给出一些基本参数就能得到所需图形,这类函数称为高层绘图函数。
此外,Matlab还提供了直接对图形句柄进行操作的低层绘图操作。
这类操作将图形的每个图形元素(如坐标轴、曲线、文字等)看做一个独立的对象,系统给每个对象分配一个句柄,可以通过句柄对该图形元素进行操作,而不影响其他部分。
本章介绍绘制二维和三维图形的高层绘图函数以及其他图形控制函数的使用方法,在此基础上,再介绍可以操作和控制各种图形对象的低层绘图操作。
一.二维绘图二维图形是将平面坐标上的数据点连接起来的平面图形。
可以采用不同的坐标系,如直角坐标、对数坐标、极坐标等。
二维图形的绘制是其他绘图操作的基础。
一.绘制二维曲线的基本函数在Matlab中,最基本而且应用最为广泛的绘图函数为plot,利用它可以在二维平面上绘制出不同的曲线。
1.plot函数的基本用法plot函数用于绘制二维平面上的线性坐标曲线图,要提供一组x坐标和对应的y坐标,可以绘制分别以x和y为横、纵坐标的二维曲线。
plot函数的应用格式plot(x,y)其中x,y为长度相同的向量,存储x坐标和y坐标。
例51在[0,2pi]区间,绘制曲线程序如下:在命令窗口中输入以下命令>>x=0:pi/100:2*pi;>>y=2*exp(-0.5*x).*sin(2*pi*x);>>plot(x,y)程序执行后,打开一个图形窗口,在其中绘制出如下曲线注意:指数函数和正弦函数之间要用点乘运算,因为二者是向量。
例52绘制曲线这是以参数形式给出的曲线方程,只要给定参数向量,再分别求出x,y向量即可输出曲线:>>t=-pi:pi/100:pi;>>x=t.*cos(3*t);>>y=t.*sin(t).*sin(t);>>plot(x,y)程序执行后,打开一个图形窗口,在其中绘制出如下曲线以上提到plot函数的自变量x,y为长度相同的向量,这是最常见、最基本的用法。
第2章 MATLAB二维绘图22.1 二维绘图基本流程22.2 二维图形的基本绘图命令42.2.1 高级绘图命令42.2.2低级绘图命令62.2 二维图形的修饰82.2.1 坐标轴的调整82.2.1.1 调整坐标轴的围82.2.1.2 调整坐标轴的状态92.2.1.3 保存坐标轴的围112.2.1.4 保存坐标轴的状态112.2.2画出或取消网格线122.2.3设置坐标轴的名称122.2.4设置图形标题132.2.5在图形中显示文字142.2.5.1用坐标轴确定文字位置142.2.5.2用鼠标确定位置显示文字152.2.6 图形的标定和颜色条162.2.7 使用绘图工具栏标注图形182.3 填充图形的绘制192.4 多坐标系绘图与图形窗口的分割202.4.1 图形叠印法202.4.2 子图的绘制212.5 特殊坐标图形的绘制222.5.1 绘制极坐标图形232.5.2对数/半对数坐标系绘图232.6 特殊二维图形的绘制242.4.3 直方图242.4.1 柱状图和面积图262.4.2 饼图282.4.4 离散数据绘图282.4.5 等高线图302.4.6 向量图312.7 函数绘图342.7.1 fplot函数342.7.2函数function的定义352.8 工作空间直接绘图362.9 手工绘图方式382.10 小结41第2章 MATLAB二维绘图数据可视化是MATLAB一项重要功能,它所提供的丰富绘图功能,使得从繁琐的绘图细节中脱离出来,而能够专心于最关心的本质。
通过数据可视化的方法,工程科研人员可以对自己的样本数据的分布、趋势特性有一个直观的了解。
本章将重点介绍MATLAB二维图形的绘制方式,并按照完整的步骤来说明一个图形产生的流程,以便将数据以图形形式来识别。
通过本章,读者不仅能掌握二维绘图的基本流程,而且能熟练使用MATLAB中相应的绘图命令、函数来绘制二维图形。
2.1 二维绘图基本流程在MATLAB中绘制图形,通常采用以下7个步骤:(1)准备数据;(2)设置当前绘图区;(3)绘制图形;(4)设置图形中曲线和标记点格式;(5)设置坐标轴和网格线属性;(6)标注图形;(7)保存和导出图形。
常用的二维图形命令:plot:绘制二维图形loglog:用全对数坐标绘图semilogx:用半对数坐标(X)绘图semilogy:用半对数坐标(Y)绘图fill:绘制二维多边填充图形polar:绘极坐标图bar:画条形图stem:画离散序列数据图stairs:画阶梯图errorbar:画误差条形图hist:画直方图fplot:画函数图title:为图形加标题xlabel:在X轴下做文本标记ylabel:在Y轴下做文本标记zlabel:在Z轴下做文本标记text:文本注释grid:对二维三维图形加格栅绘制单根二维曲线plot函数,基本调用格式为:plot(x,y)其中x和y为长度相同的向量,分别用于存储x坐标和y坐标数据。
例如:在0≤x≤2?区间内,绘制曲线y=2e-0.5xcos(4πx)程序如下:x=0:pi/100:2*pi;y=2*exp(-0.5*x).*cos(4*pi*x);plot(x,y)plot函数最简单的调用格式是只包含一个输入参数:plot(x)在这种情况下,当x是实向量时,以该向量元素的下标为横坐标,元素值为纵坐标画出一条连续曲线,这实际上是绘制折线图。
p=[22,60,88,95,56,23,9,10,14,81,56,23];plot(p)绘制多根二维曲线1.plot函数的输入参数是矩阵形式(1) 当x是向量,y是有一维与x同维的矩阵时,则绘制出多根不同颜色的曲线。
曲线条数等于y矩阵的另一维数,x被作为这些曲线共同的横坐标。
(2) 当x,y是同维矩阵时,则以x,y对应列元素为横、纵坐标分别绘制曲线,曲线条数等于矩阵的列数。
(3) 对只包含一个输入参数的plot函数,当输入参数是实矩阵时,则按列绘制每列元素值相对其下标的曲线,曲线条数等于输入参数矩阵的列数。
当输入参数是复数矩阵时,则按列分别以元素实部和虚部为横、纵坐标绘制多条曲线。
2.含多个输入参数的plot函数调用格式为:plot(x1,y1,x2,y2,…,xn,yn)(1) 当输入参数都为向量时,x1和y1,x2和y2,…,xn和yn分别组成一组向量对,每一组向量对的长度可以不同。
Matlab⼊门教程-⼆维绘图[z] MATLAB不但擅长於矩阵相关的数值运算,也适合⽤在各种科学⽬视表⽰(Scientific visualization)。
本节将介绍MATLAB基本xy平⾯及xyz空间的各项绘图命令,包含⼀维曲线及⼆维曲⾯的绘制、列印及存档。
plot是绘制⼀维曲线的基本函数,但在使⽤此函数之前,我们需先定义曲线上每⼀点的x及y座标。
下例可画出⼀条正弦曲线:close all; x=linspace(0, 2*pi, 100); % 100个点的x座标y=sin(x); % 对应的y座标plot(x,y);====================================================⼩整理:MATLAB基本绘图函数plot: x轴和y轴均为线性刻度(Linear scale)loglog: x轴和y轴均为对数刻度(Logarithmic scale)semilogx: x轴为对数刻度,y轴为线性刻度semilogy: x轴为线性刻度,y轴为对数刻度====================================================若要画出多条曲线,只需将座标对依次放⼊plot函数即可:plot(x, sin(x), x, cos(x));若要改变颜⾊,在座标对后⾯加上相关字串即可:plot(x, sin(x), 'c', x, cos(x), 'g');若要同时改变颜⾊及图线型态(Line style),也是在座标对后⾯加上相关字串即可:plot(x, sin(x), 'co', x, cos(x), 'g*');====================================================⼩整理:plot绘图函数的叁数字元颜⾊字元图线型态y 黄⾊ . 点k ⿊⾊ o 圆w ⽩⾊ x xb 蓝⾊ + +g 绿⾊ * *r 红⾊ - 实线c 亮青⾊ : 点线m 锰紫⾊ -. 点虚线-- 虚线====================================================图形完成后,我们可⽤axis([xmin,xmax,ymin,ymax])函数来调整图轴的范围:axis([0, 6, -1.2, 1.2]);此外,MATLAB也可对图形加上各种注解与处理:xlabel('Input Value'); % x轴注解ylabel('Function Value'); % y轴注解title('Two Trigonometric Functions'); % 图形标题legend('y = sin(x)','y = cos(x)'); % 图形注解grid on; % 显⽰格线我们可⽤subplot来同时画出数个⼩图形於同⼀个视窗之中:subplot(2,2,1); plot(x, sin(x));subplot(2,2,2); plot(x, cos(x));subplot(2,2,3); plot(x, sinh(x));subplot(2,2,4); plot(x, cosh(x));MATLAB还有其他各种⼆维绘图函数,以适合不同的应⽤,详见下表。
MATLAB 的二维绘图基础了解了MATLAB 的矩阵和向量概念与输入方法之后,MATLAB 的二维绘图再简单也不过了。
假设有两个同长度的向量 x 和y, 则用plot(x,y) 就可以自动绘制画出二维图来。
如果打开过图形窗口,则在最近打开的图形窗口上绘制此图,如果未打开窗口,则开一个新的窗口绘图。
〖例〗正弦曲线绘制:>> t=0:.1:2*pi;%生成横坐标向量,使其为0,0.1,0.2,...,6.2y=sin(t); % 计算正弦向量plot(t,y) %绘制图形这样立即可以得出如图所示的二维图[4.1(a)]plot() 函数还可以同时绘制出多条曲线,其调用格式和前面不完全一致,但也好理解。
>> y1=cos(t); plot(t,y,t,y1); %或plot(t,[y; y1]), 即输出为两个行向量组成的矩阵。
图形见 4.1(b)。
plot() 函数最完整的调用格式为:>> plot(x1,y1,选项1, x2,y2, 选项2, x3,y3, 选项3, ...)其中所有的选项如表 4.1 所示。
一些选项可以连用,如'-r' 表示红色实线。
由MATLAB 绘制的二维图形可以由下面的一些命令简单地修饰。
如>> xlabel('字符串') % 给横坐标轴加说明>> ylabel('字符串') % 给纵坐标轴加说明,%并自动旋转90度>> title('字符串') % 给整个图形加图题得出的图形如右图所示。
axis() 函数可以手动地设置x,y 坐标轴范围还可以使用plotyy() 函数绘制具有两个纵坐标刻度的图形。
坐标系的分割在MATLAB 图形绘制中是很有特色的,比较规则的分割方式是用subplot() 函数定义的,其标准调用格式为subplot(n,m,k)其中,n 和m 为将图形窗口分成的行数和列数,而k 为相对的编号。
.实验报告(201 /201 学年第学期)课程名称实验名称二维图形与三维图形的绘制实验时间年月日实验室指导教师学生姓名学号班级专业实验报告三、实验内容及原理(包括硬件原理图、算法、逻辑框图,关键代码等,可续页)(一)二维图形的绘制1、绘制二维曲线的基本函数:○1plot函数plot函数的基本调用格式为:plot(x,y);其中x和y为长度相同的向量,分别用于存储x坐标和y坐标数据。
例,绘制参数方程曲线。
程序如下:含多个输入参数的plot函数调用格式为:p lot(x1,y1,x2,y2,…,xn,yn);含选项的plot函数调用格式为:plot(x1,y1,选项1,x2,y2,选项2,…,xn,yn,选项n);例,用不同线型和颜色在同一坐标内绘制曲线y=2e-0.5x sin(2πx)及其包络线。
程序如下:○2双纵坐标函数plotyyplotyy函数是MATLAB 5.X新增的函数。
它能把函数值具有不同量纲、不同数量级的两个函数绘制在同一坐标中。
调用格式为:plotyy(x1,y1,x2,y2);其中x1-y1对应一条直线,x2-y2对应另一条曲线。
横坐标的标度相同,纵坐标有两个,左纵坐标用于x1-y1数据对,右纵坐标用于x2-y2数据对。
2、绘制二维图形的其他函数在线性直角坐标系中,其他形式的图形有条形图、阶梯图、杆图和填充图等,所采用的函数分别是:bar(x,y,选项);stairs(x,y,选项);stem(x,y,选项);fill(x1,y1,选项1,x2,y2,选项2,…);例,分别以条形图、填充图、阶梯图和杆图形式绘制曲线y=2e-0.5x。
程序如下:(二)三维图形的绘制1、绘制三维曲线的基本函数plot3函数与plot函数用法十分相似,其调用格式为:plot3(x1,y1,z1,选项1,x2,y2,z2,选项2,…,xn,yn,zn,选项n); 例,绘制空间曲线。
程序如下:2、绘制三维曲面的函数surf函数和mesh函数的调用格式为:surf(x,y,z,e);mesh(x,y,z,e);例,绘制两个直径相等的圆管的相交图形。
《MATLAB语言》课程论文利用MATLAB绘制二维函数图形姓名:海燕学号:***********专业:通信工程班级:通信一班指导老师:***学院:物理电气信息学院成日期:2011年12月5利用MATLAB绘制二维函数图形(海燕12010245375 2010级通信1班)[摘要]大学高等数学中涉及许多复杂的函数求导绘图极值及其应用的问题,例如二维绘图,对其手工绘图因为根据函数的表达式的难易程度而不易绘制,而MATLAB语言正是处理这类的很好工具,既能简易的写出表达式,又能绘制有关曲线,非常方便实用。
另外,利用其可减少工作量,节约时间,加深理解,同样可以培养应用能力。
本文将探讨利用matlab来解决高等数学中的二维图形问题,并对其中的初等函数、极坐标、进行实例分析,对于这些很难用手工绘制的图形,利用matlab则很轻易地解决。
[关键词]高等数学一元函数二元函数MATLAB语言图形绘制一、问题的提出MATLAB 语言是当今国际上科学界(尤其是自动控制领域) 最具影响力、也是最有活力的软件。
它提供了强大的科学运算、灵活的程序设计流程、高质量的图形可视化与界面设计、便捷的与其他程序和语言接口的功能。
中学数学中常见到的是二维平面图形,由于概念抽象,学生不好理解,致使学生对学习失去信心,导致学习兴趣转移。
在传统的教学中,教师在黑板上应用教具做图,不能保证所做图形的准确性,曲线的光滑度不理想,教学过程显得枯燥无味,教学质量难以保证。
Matlab是集数值计算、符号计算和图形可视化三大基本功能于一体的大型软件,广泛应用于科学研究、工程计算、动态仿真等领域。
Matlab是一种集成了计算功能、符号运算、数据可视化等强大功能的数学工具软件。
其代码的编写过程与数学推导过程的格式很接近,所以使编程更为直观和方便,应用于教学就更加容实现Matlab软件尤其在简单的绘图中有较强的编辑图形界面功能,在中学的数学教学中的抽象函数变得直观形象、容易实现,同时也激发学生的学习兴趣,学生通过数形结合,更好地理解题意高等数学是一门十分抽象的学科,对于一些抽象的函数,我们可以借助于几何图形来理解,但这类图形的绘制往往很复杂,仅凭手工绘制也难以达到精确的效果,这时如果使用Matlab 来解决所遇到的图形问题,则能达到事半功倍的效果。
在高等数学领域中有关图形方面的应用,无论是初等函数图形、还是极坐标图形、统计图,对于Matlab而言都是完全可以胜任的。
下面结合实例从几个方面来阐述matlab在高等数学二维图形中的应用。
二、用matlab绘制一元函数图像1.平面曲线的表示形式对于平面曲线,常见的有三种表示形式,即以直角坐标方程],[),(baxxfy∈=,以参数方程],[),(),(battyytxx∈==,和以极坐标],[),(barr∈=ϕϕ表示等三种形式。
2.曲线绘图的MATLAB命令MATLAB中主要用plot,fplot二种命令绘制不同的曲线。
plot(x,y) 作出以数据(x(i),y(i))为节点的折线图,其中x,y 为同维数的向量。
plot(x1,y1,x2,y2,…) 作出多组数据折线图fplot(‘fun’,[a,b]) 作出函数fun 在区间[a,b]上的函数图。
可以用help plot, help fplot 查阅有关这些命令的详细信息问题1 作出函数x y x y cos ,sin ==的图形,并观测它们的周期性。
先作函数x y sin =在]4,4[ππ-上的图形,用MATLAB 作图的程序代码为:>>x=linspace(-4*pi,4*pi,300); %产生300维向量x>>y=sin(x); %正玄函数>>plot(x,y) %二维图形绘图命令结果如图1所示图1 x y sin =的图形此图也可用fplot 命令,相应的MATLAB 程序代码为:>>clear; close; %clear 清理内存;close 关闭已有窗口。
>>fplot('sin(x)',[-4*pi,4*pi]) %绘制正玄图形结果如图2所示图2xy sin=的图形如果在同一坐标系下作出两条曲线xy sin=和xy cos=在]2,2[ππ-上的图形,相应的MATLAB程序代码为:>>x=-2*pi:2*pi/30:2*pi; %产生向量x>>y1=sin(x); y2=cos(x); %正余玄函数>>plot(x,y1,x,y2,’:’)%’:’表示绘出的图形是点线结果如图3所示其中实线是xy sin=的图形,点线是xy cos=的图形。
图3xyxy cos,sin==的图形问题2.将图3用不同的线型及颜色加以绘制。
>>x=-2*pi:2*pi/30:2*pi; %产生向量x>>y1=sin(x); y2=cos(x); %正余玄函数>>plot(x,y1,x,y2,’gp’)%’ gp’表示绘出的图形是绿色五角星线结果如图4图4不同线型与颜色绘制的正余玄图形问题3作出以极坐标方程]2,0[,1),cos1(πϕϕ∈=+=aar表示的心脏线相应的MATLAB程序代码为:>>clear; close; %clear清理内存;close关闭已有窗口>>t=0:2*pi/30:2*pi; % 产生向量t>>r=1+cos(t); %极坐标方程>>x=r.*cos(t); y=r.*sin(t); %极坐标转化为直角坐标>>plot(x,y) %绘制x,y的图形结果如图5所示图5脏线三、用matlab绘制分段函数图像在绘制图形的同时,可以对图形加上一些说明,如图形名称,坐标轴说明以及某一部分的含义等,这些操作称为添加图形标注,下面就举例说明。
问题4 绘制分段函数曲线并添加图形标注f(x)=sqrt(x) 时0<=x<4 f(x)=2时4<=x<6 f(x)=5-2/x时6<=x<8 f(x)=1时x>=8 相应的MATLAB程序代码为:X=linspace(0,10,100);%产生一个行向量XY=[]; %产生一个函数值for x0=x %用循环语句判断函数值问题if x0>=8 y=[y,1]; %条件语句elseif x0>=6 y=[y,5-x0/2]; %条件语句elseif x0>=4 y=[y,2]; %条件语句elseif x0>=0 y=[y,sqrt(x0)]; %条件语句end %结束语句end %结束语句plot(x,y) %绘制X,Y图形axis([0 10 2.5]) %设置坐标轴title(’分段函数曲线’);%加图形变体xlabel(’variable X’); %加X轴说明ylabel(‘variable Y’);%加Y轴说明text(2,1.3,’y=x^{1/2}’); %在指定位置添加图形说明text(4.5,1.9,’y=2’); %在指定位置添加图形说明text(7.3,1.5,’y=5-x/2’); %在指定位置添加图形说明text(8.5,0.9,’y=1’); %在指定位置添加图形说明结果如图6所示图6 一元分段函数图四用matlab绘制二维隐函数图形function implot(fun,rangexy,ngrid) %二维隐函数绘图%输入参数说-fun 函数句柄,可以是匿名、inline和M函数该函数就是调用了contour()函数,绘制隐函数在xoy平面上的等高线,就得到了二维隐函数的图像-rangexy=[xmin xmax ymin ymax] 绘图范围,默认[-2*pi 2*] -ngrid 绘图时计算的点数,初值是20,然后逐步加细,默认50。
五.用matlab绘制二元函数图像1.曲面绘图的MATLAB命令MATLAB中主要用mesh,surf命令绘制二元函数图形。
mesh(x,y,z) 画网格曲面,这里x,y,z是三个数据矩阵,分别表示数据点的横坐标,纵坐标和函数值,该命令将数据点在空间中描出,并连成网格。
surf(x,y,z) 画完整曲面,这里x,y,z是三个数据矩阵,分别表示数据点的横坐标,纵坐标和函数值,该命令将数据点所表示曲面画出。
问题5画出函数22yxz+=的二维等高线图形,不妨将区域限制在]3,3[]3,3[),(-⨯-∈yx。
则用MATLAB作图的程序代码为:>>clear; %清理内存x=-3:0.1:3; %X的范围【-3,3】y=-3:0.1:3; %y的范围【-3,3】>>[X,Y]=meshgrid(x,y); %将向量x,y指定的区域转化为矩阵X,Y Z=sqrt(X.^2+Y.^2); %产生函数值Z>> contour(X,Y,Z,10) %画10条等高线>>xlabel('X-axis'),ylabel('Y-axis')%两个坐标轴标记>>title('Contour of Surface') %标题>>grid on %画网格线结果如图7所示1图7 等高线如果要画1 z 的等高线,则用命令>>clear; %清理内存x=-3:0.1:3; %x 的范围【-3,3】y=-3:0.1:3; %y 的范围【-3,3】>>[X,Y]=meshgrid(x,y); %将向量x,y 指定的区域转化为矩阵X,YZ=sqrt(X.^2+Y.^2); %产生函数值z>> contour(X,Y,Z,[1 1]) %画 z=1时的等高线结果如图8所示图8 z=1时的等高线五、结论从以上利用MATLAB语言对3种基本函数的二维图形的绘制的分析我们不难得出以下结论:二维图形的绘制是其他回吐操作的基础。
在matlab中,最基本且应用最为广泛的绘图函数为plot函数,利用它可以在二维平面上绘制出不同的曲线。
Plot函数用于绘制xy平面上的线性坐标曲线图需要提供一组x坐标及其各点对应的y坐标,这样就可以绘制出分别以x,y为横纵坐标的二维曲线。
Matlab还提供了一些绘图选项,用于确定所绘曲线的线性,颜色和数据点标记符号,它们可以组合使用。
数据点可以用向量或矩阵的形式给出,类型可以是实型或复型,在取数据点时一般都是等间隔采样,这对绘制高频率变化的函数不够精确,为提高精度,绘制出比较真实的函数曲线,就不能等间隔取样,而必须在变化率大的区段密集采样,以充分反映函数的变化规律,进而提高图形的真实性。