逻辑学真值表及命题演算.ppt

离散数学命题公式和真值表第2讲命题常项犹如数学中常量（a,b,c ）命题变项犹如数学中变量（x,y,z ）确指的或具体的命题。

命题常项命题变项不确指的或抽象的命题。

命题常项与命题变项都用p,q,r…等表示。

对命题变项p而言，p只是一个标识，可以用任何一个具体的命题替代。

命题公式将命题常项（即1，0）和命题变项用联结词和圆括号按一定的逻辑关系联结起来的符号串。

(1)(2)单个命题常项和命题变项是命题公式，称为原子公式。

若A是命题公式，则(⎤A)也是命题公式。

(3)若A，B是命题公式，则(A∧B)，(A∨B)，(A→B)，(A↔B)也是命题公式。

(4)由有限次地应用(2)~(3)形成的符号串是命题公式。

定义2.1（命题公式）注意1设A是公式，B为A中连续的一部分，若B也是公式，则称B为A的子公式。

2公式最外层的括号可以去掉。

注意3优先级规定（1）各联结词运算的优先级为：⎤，∧，∨，→，↔。

（2）对于同一级者一目，从右向左二目，从左到右（3）括号优先，从里到外。

注意根据运算优先级的规定不必要的括号也可以去掉。

如:（p∨q)∨(⎤r)可写为p∨q∨⎤r真值表公式的解释和赋值将公式中的每个命题变项都指定一个具体的命题，抽象的公式就具有了实际的意义，成了命题，具有了真值，这称为公式的解释。

对公式的解释相当于是将指定为真（假）命题的命题变项赋值1（0）。

真命题假命题赋值1赋值0命题变项定义2.2（公式的赋值）设p1 ，p2 ，…，p n是出现在公式A中的全部的命题变项，给p1，p2，…，p n各指定一个真值，称为对A的一个赋值。

定义2.2（公式的赋值）将n个命题变项按下标顺序或字典顺序排列后，赋值就相当于一长为n的0，1字符串。

思考含有n个命题变项的公式共有多少个不同的赋值？SAT（适定性问题）给一个命题公式，它是否存在一个成真赋值？1971年Cook证明：SAT问题是（第一个）NPC问题。

定义2.3（真值表）将命题公式A在所有赋值下取值情况列成表，称做A的真值表。

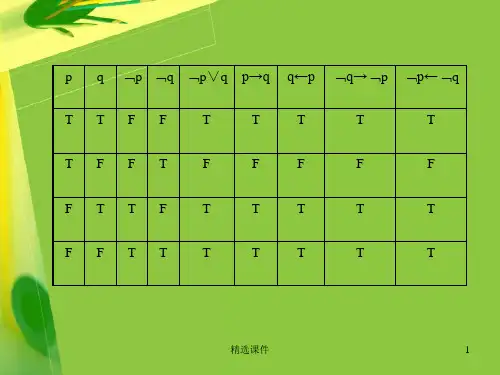
联言判断
包含两个联言支的联言判断，其逻辑形式可表示为：p并且q，合取式为：p∧q
联言判断的真假（真值表）
选言判断
1、相容选言判断
逻辑形式：p或者q，p∨q
真假表表明：p∨q假，当且仅当p和q同假。

2、不相容选言判断
逻辑形式：要么p，要么q, p∨q
真值表表明：p∨q假，当且仅当p和q同真或同假。

假言判断
充分条件假言判断
1、充分条件假言判断：
真假表表明：p →q为假，当且仅当p真而q假。

2、必要条件假言判断：
真值表表明：p ←q为假，当且仅当p假而q真
3、充分必要条件假言判断
真值表表明：p q 真，当且仅当p 和q 同真或同假。

p q p q
T T T
T F F
F T F
F F T
负判断
逻辑形式：并非p ，逻辑符号表示：“
”或者“ ”
T F
F T
•
p p p。