第二章+(4)非确定有限自动机NFA

编译原理nfa
编译原理中的NFA，是指非确定有限状态自动机（Nondeterministic Finite Automata）。

在计算机科学中，NFA是一种有限状态自动机，它可以用于描述一类模式匹配问题。

NFA由一组状态、一组输入符号、一个转移函数、一个初始状态和一组接受状态组成。

与确定性有限状态自动机（DFA）相比，NFA在某些方面具有更高的表达能力，因为它允许在同一时刻有多个状态，并且在输入符号为空时可以不进行转移。

但由于NFA的非确定性，使用NFA进行模式匹配时，需要进行转换和回溯，增加了计算的复杂度。

在编译原理中，NFA通常用于描述正则表达式的语法结构和匹配算法。

编译器在识别程序中的正则表达式时，会将其转换为NFA，并使用NFA进行模式匹配和语义分析。

通过这种方式，可以实现高效的正则表达式匹配和语法分析。

总之，NFA是编译原理中非常重要的概念，它为编译器设计和实现提供了一种有效的工具，能够实现正则表达式匹配和其他相关问题的解决。

简述有限状态机的分类和区别
有限状态机是计算机科学中的一种数学模型，用于描述系统的状态转换行为。

根据状态转换的规则和方式，可以将有限状态机分为两类：确定性有限状态机和非确定性有限状态机。

确定性有限状态机（Deterministic Finite Automaton，DFA）
指的是状态转换是唯一的，即在任何时候，从任何状态出发，只要读入相同的输入符号，都会到达同一个状态。

这种状态机的状态转换图是一个有向无环图，每个状态只有一个后继状态。

非确定性有限状态机（Nondeterministic Finite Automaton，NFA）指的是状态转换不唯一，即在某些情况下，从同一状态出发，
读入相同的输入符号，可能会到达不同的状态。

这种状态机的状态转换图是一个有向图，每个状态可能有多个后继状态。

在实际应用中，有限状态机还可以根据状态的数量、输入符号的类型、输出符号的类型等进行分类。

例如，根据状态数量的不同，可以将有限状态机分为有限自动机和无限自动机；根据输入符号的类型，可以将有限状态机分为确定性和非确定性的输入符号型有限状态机等。

总之，有限状态机是一种非常重要的计算机模型，能够描述许多复杂的系统行为。

了解有限状态机的分类和区别，可以更好地理解和应用它们。

- 1 -。

第二章 词法分析2.1 完成下列选择题：(1) 词法分析器的输出结果是。

a. 单词的种别编码b. 单词在符号表中的位置c. 单词的种别编码和自身值d. 单词自身值(2) 正规式M1和M2等价是指。

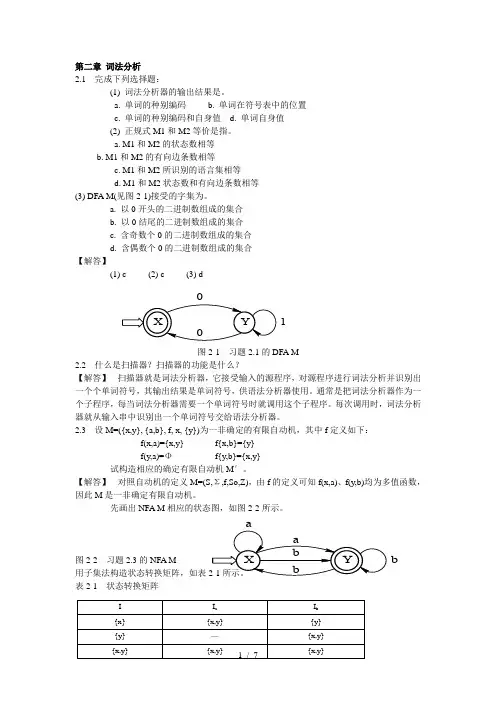
a. M1和M2的状态数相等b. M1和M2的有向边条数相等c. M1和M2所识别的语言集相等d. M1和M2状态数和有向边条数相等(3) DFA M(见图2-1)接受的字集为。

a. 以0开头的二进制数组成的集合b. 以0结尾的二进制数组成的集合c. 含奇数个0的二进制数组成的集合d. 含偶数个0的二进制数组成的集合【解答】(1) c (2) c (3) d图2-1 习题2.1的DFA M2.2 什么是扫描器？扫描器的功能是什么？【解答】 扫描器就是词法分析器，它接受输入的源程序，对源程序进行词法分析并识别出一个个单词符号，其输出结果是单词符号，供语法分析器使用。

通常是把词法分析器作为一个子程序，每当词法分析器需要一个单词符号时就调用这个子程序。

每次调用时，词法分析器就从输入串中识别出一个单词符号交给语法分析器。

2.3 设M=({x,y}, {a,b}, f, x, {y})为一非确定的有限自动机，其中f 定义如下：f(x,a)={x,y} f {x,b}={y}f(y,a)=Φ f{y,b}={x,y}试构造相应的确定有限自动机M ′。

【解答】 对照自动机的定义M=(S,Σ,f,So,Z)，由f 的定义可知f(x,a)、f(y,b)均为多值函数，因此M 是一非确定有限自动机。

先画出NFA M 相应的状态图，如图2-2所示。

图2-2 习题2.3的NFA M 用子集法构造状态转换矩阵，如表表2-1 状态转换矩阵1b将转换矩阵中的所有子集重新命名，形成表2-2所示的状态转换矩阵，即得到 M ′=({0,1,2},{a,b},f,0,{1,2})，其状态转换图如图2-3所示。

表2-2 状态转换矩阵将图2-3所示的DFA M ′最小化。

第三章3.1 对于词法分析器的要求1．词法词法分析的任务：从左至右逐个字符地对源程序进行扫描，产生一个个单词符号。

词法分析器(Lexical Analyzer) 又称扫描器(Scanner)：执行词法分析的程序。

2．程序语言的单词符号：关键字、标识符、常数、运算符、界符。

3．输出的单词符号的表示形式:(单词种别，单词自身的值)Eg：while (i>=j) i--;输出单词符号：< while, - >< (, - >< id, 指向i的符号表项的指针><>=, - >< id, 指向j的符号表项的指针>< ), - >< id, 指向i的符号表项的指针>< --, - >< ;, - >4．词法分析器作为一个独立子程序：结构简洁、清晰和条理化，有利于集中考虑词法分析一些枝节问题。

5．词法分析器3.2 词法分析器的设计1．词法分析器2．输入、预处理：输入串放在输入缓冲区中。

预处理子程序：剔除无用的空白、跳格、回车和换行等编辑性字符;区分标号区、捻接续行和给出句末符等扫描缓冲区（指向开始位置，向前搜索确定终点）3．单词符号的识别、超前搜索：(1)基本字识别Eg：DO99K=1，10 DO 99 K = 1，10IF(5.EQ.M)GOTO55 IF (5.EQ.M) GOTO 55DO99K=1.10IF(5)=55需要超前搜索才能确定哪些是基本字(2)标识符(3)常数(4)算符和界符4．状态转换图(有限方向图)<1>结点代表状态<2>状态之间用箭弧连结，箭弧上的标记(字符)代表射出结状态下可能出现的输入字符或字符类。

<3>一个状态转换图可用于识别(或接受)一定的字符串。

5．语法分析的状态转换图6．状态转换图的实现思想：每个状态结对应一小段程序。

概念记号有字母表中的符号组成的有限长度的序列。

记号s的长度记为|s|。

长度为0的记号称为空记号，记为ε。

有限自动机(Finite State Automaton)为研究某种计算过程而抽象出的计算模型。

拥有有限个状态，根据不同的输入每个状态可以迁移到其他的状态。

非确定有限自动机(Nondeterministic Finite Automaton)简称NFA，由以下元素组成：1. 有限状态集合S；2. 有限输入符号的字母表Σ；3. 状态转移函数move；4. 开始状态sSUB{0}；5. 结束状态集合F，F ∈ S。

自动机初始状态为sSUB{0}，逐一读入输入字符串中的每一个字母，根据当前状态、读入的字母，由状态转移函数move控制进入下一个状态。

如果输入字符串读入结束时自动机的状态属于结束状态集合F，则说明该自动机接受该字符串，否则为不接受。

确定有限自动机(Deterministic Finite Automaton)简称DFA，是NFA的一种特例，有以下两条限制：1. 对于空输入ε，状态不发生迁移；2. 某个状态对于每一种输入最多只有一种状态转移。

将正则表达式转换为NFA(Thompson构造法)算法算法1将正则表达式转换为NFA(Thompson构造法)输入字母表Σ上的正则表达式r输出能够接受L(r)的NFA N方法首先将构成r的各个元素分解，对于每一个元素，按照下述规则1和规则2生成NFA。

注意：如果r中记号a出现了多次，那么对于a的每次出现都需要生成一个单独的NFA。

之后依照正规表达式r的文法规则，将生成的NFA按照下述规则3组合在一起。

规则1对于空记号ε，生成下面的NFA。

规则2对于Σ的字母表中的元素a，生成下面的NFA。

规则3令正规表达式s和t的NFA分别为N(s)和N(t)。

a) 对于s|t，按照以下的方式生成NFA N(s|t)。

b) 对于st，按照以下的方式生成NFA N(st)。

第二章 词法分析2.1 完成下列选择‎题： (1) 词法分析器的‎输出结果是 。

a. 单词的种别编‎码 b. 单词在符号表‎中的位置 c. 单词的种别编‎码和自身值 d. 单词自身值 (2) 正规式M1和‎M 2等价是指‎ 。

a. M1和M2的‎状态数相等b. M1和M2的‎有向边条数相‎等c. M1和M2所‎识别的语言集‎相等d. M1和M2状‎态数和有向边‎条数相等 (3) DFA M(见图2-1)接受的字集为‎ 。

a. 以0开头的二‎进制数组成的‎集合b. 以0结尾的二‎进制数组成的‎集合c. 含奇数个0的‎二进制数组成‎的集合d. 含偶数个0的‎二进制数组成‎的集合 【解答】(1) c (2) c (3) d图2-1 习题2.1的DFA M2.2 什么是扫描器‎？扫描器的功能‎是什么？ 【解答】 扫描器就是词‎法分析器，它接受输入的‎源程序，对源程序进行‎词法分析并识‎别出一个个单‎词符号，其输出结果是‎单词符号，供语法分析器‎使用。

通常是把词法‎分析器作为一‎个子程序，每当词法分析‎器需要一个单‎词符号时就调‎用这个子程序‎。

每次调用时，词法分析器就‎从输入串中识‎别出一个单词‎符号交给语法‎分析器。

2.3 设M=({x,y}, {a,b}, f, x, {y})为一非确定的‎有限自动机，其中f 定义如‎下： f(x,a)={x,y} f{x,b}={y} f(y,a)=Φ f{y,b}={x,y} 试构造相应的‎确定有限自动‎机M ′。

【解答】 对照自动机的‎定义M=(S,Σ,f,So,Z)，由f 的定义可‎知f(x,a)、f(y ,b)均为多值函数‎，因此M 是一非‎确定有限自动‎机。

先画出NFA ‎ M 相应的状态‎图，如图2-2所示。

图2-2 习题2.3的NFA M用子集法构造‎状态转换矩阵‎，如表表2-1 状态转换矩阵‎1b将转换矩阵中‎的所有子集重‎新命名，形成表2-2所示的状态‎转换矩阵，即得到 M ′=({0,1,2},{a,b},f,0,{1,2})，其状态转换图‎如图2-3所示。

不确定有限状态自动机的确定化(NFA TO DFA)不确定有限状态自动机的确定化(NFA TO DFA 2008-12-05 22:11#in clude<iostream>#in clude<stri ng>#defi ne MAXS 100using n amespace std;string NODE; // 结点集合stri ng CHANGE; // 终结符集合int N; //NFA 边数struct edge{stri ng first;stri ng cha nge;stri ng last;};struct cha n{stri ng ltab;stri ng jihe[MAXS];};void kon g(i nt a){int i;for(i=0;i<a;i++)cout«'';}//排序void paixu(stri ng &a){int i,j;char b;for(j=0;j<a」en gth();j++)for(i=0;i<a」en gth();i++)if(NODE.fi nd(a[i])>NODE.fi nd(a[i+1])){b=a[i];a[i]=a[i+1];a[i+1]=b;void eclouse(char c,stri ng &he,edge b[]){int k;for(k=0;k<N;k++){if(c==b[k].first[0])if(b[k].cha nge=="*"){if(he.fi nd(b[k].last)>he.le ngth())he+=b[k].last; eclouse(b[k].last[0],he,b);}}}void move(cha n &he,i nt m,edge b[]){int i,j,k,l;k=he .l tab .len gth();l=he.jihe[m].le ngth();for(i=0;i<k;i++)for(j=0;j<N;j++)if((CHANGE[m]==b[j].cha nge[0])&&(he.ltab[i]==b[j].first[0])) if(he.jihe[m].find(b[j].last[0])>he.jihe[m].le ngth()) he.jihe[m]+=b[j].last[0];for(i=0;i<l;i++)for(j=0;j<N;j++)if((CHANGE[m]==b[j].cha nge[0])&&(he.jihe[m][i]==b[j].first[0] ))if(he.jihe[m].fi nd(b[j].last[0])>he.jihe[m].le ngth()) he.jihe[m]+=b[j].last[0]; }//输出void outputfa(i nt le n,i nt h,cha n *t){int i,j,m;cout«" I ";for(i=0;i<le n;i++) coutv<TvvCHANGE[i]vv" ";cout«endlvv" ------------------------- "<<e ndl;for(i=0;i<h;i++)cout«' '<<t[i].ltab;m=t[i].ltab.le ngth();for(j=0;j<le n;j++){{kon g(8-m);m=t[i].jihe[j].le ngth();cout<<t[i].jihe[j];}cout«e ndl;}}void mai n(){edge *b=new edge[MAXS];int i,j,k,m,n,h,x,y,len;bool flag;stri ng jh[MAXS],e ndno de,ed no de,sta;coutvv"请输入NFA各边信息(起点条件[空为*]终点)，以#结束："vvendl; for(i=0;i<MAXS;i++){cin> >b[i].first;if(b[i].first=="#") break;cin> >b[i].cha nge»b[i].last;}N=i;/*for(j=0;j<N;j++)cout<<b[j].firstvvb[j].cha nge<<b[j].lastvve ndl;*/for(i=0;i<N;i++){if(NODE.fi nd(b[i].first)>NODE.Ie ngth())NODE+=b[i].first;if(NODE.fi nd(b[i].last)>NODE.le ngth())NODE+=b[i].last;if((CHANGE.fi nd(b[i].cha nge)>CHANGE.Ie ngth())&&(b[i].cha nge!="*"))CHANGE+=b[i].cha nge;}len=CHANGE.le ngth();coutvv"结点中属于终态的是："<<endl;{coutvv"所输终态不在集合中，错误! "<<e ndl;cin>>endno de;for(i=0;i<e ndnode.len gth();i++)if(NODE.fi nd(e ndn ode[i])>NODE.le ngth()) {{coutvv"所输终态不在集合中，错误! "<<e ndl; return;}〃cout«"e ndno de="«e ndno de<<e ndl;chan *t=new chan [MAXS];t[O].ltab=b[O].first;h=1;for(j=0;j<le n;j++){paixu(t[i].jihe[j]);//对集合排序以便比较for(k=0;k<h;k++){flag=operator==(t[k].ltab,t[i].jihe[j]);if(flag)break;}if(!flag&&t[i].jihe[j].le ngth())t[h++].ltab=t[i].jihe[j];} }cout«endlvv"状态转换矩阵如下："<<endl;outputfa(len,h,t); II 输出状态转换矩阵eclouse(b[0].first[0],t[0].ltab,b); //cout<<t[0].ltab<<e ndl; for(i=0;i<h;i++) { for(j=0;j<t[i].ltab.le ngth();j++) for(m=0;m<le n;m++) eclouse(t[i].ltab[j],t[i].jihe[m],b); for(k=0;k<le n;k++) { 〃cout<vt[i].jihe[k]vv"->"; move(t[i],k,b); 〃cout<vt[i].jihe[k]vve ndl; for(j=0;j<t[i].jihe[k].le ngth();j++) eclouse(t[i].jihe[k][j],t[i].jihe[k],b); // } // 求 e-clouse // 求 e-clouse // 求 move(I,a) 求 e-clouse//状态重新命名NODE.erase();cout«endlvv"重命名："<<endl; for(i=0;i<h;i++)sta=t[i].ltab;{t[i].ltab.erase();t[i].ltab='A'+i;NODE+=t[i].ltab;coutvv'{'v<stavv"}="vvt[i].ltabvve ndl;for(j=0;j<e ndnode.len gth();j++)if(sta.fi nd(e ndno de[j])<sta.le ngth()) d[1]=ednode+=t[i].ltab;for(k=0;k<h;k++) for(m=0;m<le n;m++) if(sta==t[k].jihe[m])t[k].jihe[m]=t[i].ltab;}for(i=0;i<NODE.le ngth();i++)if(ed node.fi nd(NODE[i])>ed node.le ngth()) d[0]+=NODE[i]; endnode=ednode;cout«endl<v"DFA 如下："<<endl; outputfa(len,h,t); // 输出DFA cout«"其中终态为："<<endnode<<endl; //DFA最小化m=2;sta.erase();flag=0;for(i=0;i<m;i++){〃coutvv"d["vvivv"]="vvd[i]vve ndl;for(k=0;k<le n;k++){//coutv<TvvCHANGE[k]vve ndl;y=m;for(j=0;j<d[i].le ngth();j++){for(n=0;n<y;n++){if(d[ n].fi nd(t[NODE.fi nd(d[i][j])].jihe[k])<d[ n].le ngth() ||t[NODE.fi nd(d[i][j])].jihe[k].le ngth()==0){if(t[NODE.fi nd(d[i][j])].jihe[k].le ngth()==0)x=m;elsex=n;if(!sta.le ngth())sta+=x+48;{}elseif(sta[0]!=x+48){ d[m]+=d[i][j]; flag=1;d[i].erase(j,1); 〃cout<vd[i]vve ndl;j--；} break; // 跳出n}}//n}〃jif(flag){m++;flag=0;}//cout<<"sta="<<sta<<e ndl; sta.erase();}//k}//icout«endl<<"集合划分：";for(i=0;i<m;i++)cout<v"{"vvd[i]vv"}";cout«e ndl;//状态重新命名cha n *md=new cha n[ m];NODE.erase();cout«endlvv"重命名："<<endl;for(i=0;i<m;i++){md[i].ltab='A'+i;NODE+=md[i].ltab; coutvv"{"v<d[i]vv"}="vvmd[i].ltabvve ndl; }for(i=0;i<m;i++)for(k=0;k<le n;k++)for(j=0;j<h;j++){if(d[i][0]==t[j].ltab[0])for(n=0;n<m;n++){{if(!t[j].jihe[k]」e ngth()) break;elseif(d[ n].fi nd(t[j].jihe[k])<d[ n].le ngth()) {md[i].jihe[k]=md[ n] .Itab;break;}}break;}}edno de.erase();for(i=0;i<m;i++)for(j=0;j<e ndnode.len gth();j++) if(d[i].fi nd(e ndno de[j])<d[i].le ngth()&&ed node.fi nd(md[i].lta b))edno de+=md[i].ltab;endnode=ednode;cout«endlvv"最小化DFA如下："<<endl;outputfa(le n,m ,md);cout«"其中终态为："<<endnode<<endl;}/////////////////////////////////测试数据：i* 11a 11b 11 * 22a 32b 43a 54 b 55* 66 a 66 b 66 * f#////////////////////////////////请输入NFA各边信息（起点条件［空为*］终点），以#结束:i * 11 a 11b 11 * 22a 32b 43a 54 b 55* 66 a 66 b 66 * f#结点中属于终态的是：状态转换矩阵如下：I la lbi12 123 12412312356f124124123 12456f12356f12356f1246f12456f1236f 12456f1246f 1236f 12456f1236f 12356f1246f重命名：{i12}=A{123}=B{124}=C{12356f}=D{12456f}=E{1246f}=FDFA如下：I Ia Ib B D C C B E DDF E G E F G E G D F其中终态为：DEFG集合划分：{A} {DEFG} {B} {C}重命名：{A}=A{DEFG}=B{B}=C{C}=D最小化DFA如下：I la lbA C DB B BC B DD C B 其中终态为：B。

课程设计报告课程：编译原理学号：姓名：班级：教师：时间：2014.5--2014.6.20计算机科学与技术系图4.4-1 NFA-DFA处理流程图2.NFA转换为DFA的原理及过程通过以下例子说明：①假如输入的NFA如图4.4-2所示：图4.4-2 NFA状态转换图②对于图4.2-2中的状态转换图的状态转换矩阵为：在图4.2-2中的状态转换图加一个起始状态X和结束状态Y，I为起始节点X经过一个或多个ε边到达的状态集，Ia为{X,1}经过a边到达的结点的ε闭包，Ib经过b边到达的结点的ε闭包;知道Ia和Ib列都在I列中出现为止。

如下表4.2.1所示：表4.2.1状态转换矩阵I Ia Ib{X,1} {2,3,Y}{2,3,Y} {2,3,Y}③对表4.2.1的状态转换矩阵进行重新命名，令A={X,1}，B={2,3,Y}，转换结果如下表4.2.2所示：表4.2.2重命名的状态转换矩阵④表4.2.2相对应的 DFA状态转换图为下图图4.2-2所示：图4.2-2 DFA状态图I Ia IbA BB B结果与分析（可以加页）：1.对于下图1中的NFA：图1 NFA状态图2.输入图1中NFA的各边信息：如下截图图2所示：图2 输入各边信息截图3.对于图1的NFA状态转换矩阵和重命名后的状态矩阵如下截图图3所示：图3 DFA状态矩阵截图4.将图3中的状态矩阵图最小化，如下截图图4所示：图4 最小化的DFA5.根据图4最小化的DFA状态转换矩阵，画出DFA状态转换图，如下图图5所示：图5 DFA状态装换图设计体会与建议：编译原理是一门重要但难学的课程，因为编译原理是关于编写编译器的技术，编译器的编写一直被认为是十分困难的事情，所以这次选到课程设计的课题就有些无从下手的感觉，感觉任务挺艰巨的。

设计要求从理论上就不太好理解，不像以前的设计编写一个应用程序实现常见的功能，这次的课程设计注重各种算法的实现，比如用子集法实现不确定的有限自动机的确定化、又能够分割法实现确定的有限自动机的最小化。

不确定有限状态自动机的确定化【实验目的】输入：非确定有限（穷）状态自动机。

输出：确定化的有限（穷）状态自动机。

【实验原理】同一个字符串α可以由多条通路产生，而在实际应用中，作为描述控制过程的自动机，通常都是确定有限自动机DFA，因此这就需要将不确定有限自动机转换成等价的确定有限自动机，这个过程称为不确定有限自动机的确定化，即NFA确定化为DFA。

NFA确定化的实质是以原有状态集上的子集作为DFA上的一个状态，将原状态间的转换为该子集间的转换，从而把不确定有限自动机确定化。

经过确定化后，状态数可能增加，而且可能出现一些等价状态，这时就需要简化。

【程序代码】#include<iostream>#include<string>#include<vector>using namespace std;#define max 100struct edge{string first;//边的初始结点string change;//边的条件string last;//边的终点};int N;//NFA的边数vector<int> value;string closure(string a,edge *b){int i,j;for(i=0;i<a.length();i++){for(j=0;j<N;j++){if(b[j].first[0]==a[i]&&b[j].change=="&"){a=a+b[j].last[0];}}}return a;}string move(string jihe,char ch,edge *b){int i,j;string s="";for(i=0;i<jihe.length();i++){for(j=0;j<N;j++){if(b[j].first[0]==jihe[i]&&b[j].change[0]==ch)s=s+b[j].last;}}return s;}string sort(string t){int k,i,j;char tt;for(i=0;i<t.length()-1;i++){k=i;for(j=i+1;j<t.length();j++){if(t[j]<t[k])k=j;}tt=t[k];t[k]=t[i];t[i]=tt;}return t;}void main(){int i,j,x=0,h,length,m,d=0;string Change;string First,Last;//初态，终态，string T[max],ss;edge *b=new edge[max];cout<<"请输入各边信息：起点条件（空用&表示）终点，以输入#结束。