高一数学《3.1.1直线的倾斜角与斜率》

3.1.1直线的倾斜角与斜率题型全归纳【知识梳理】1.倾斜角的定义：当直线l 与x 轴相交时，取x 轴作为基准，x 轴正方向与直线l 向上方向之间所成的角叫做直线l 的倾斜角．如图所示，直线l的倾斜角是∠APx ，直线l ′的倾斜角是∠BPx .2．倾斜角的范围：直线的倾斜角α的取值范围是0°≤α＜180°，并规定与x 轴平行或重合的直线的倾斜角为0°.3．倾斜角与直线形状的关系的正切值叫做这条直线的斜率．即k ＝tan_α.5．斜率公式：经过两点P 1(x 1，y 1)，P 2(x 2，y 2)(x 1≠x 2)的直线的斜率公式为k ＝y 2－y 1x 2－x 1.当x 1＝x 2时，直线P 1P 2没有斜率．6．斜率作用：用实数反映了平面直角坐标系内的直线的倾斜程度．【常考题型】题型一、直线的倾斜角例1：若直线l 的向上方向与y 轴的正方向成30°角，则直线l 的倾斜角为( )A ．30°B ．60°C ．30°或150°D ．60°或120°变式1：直线l 经过第二、四象限，则直线l 的倾斜角范围是( )A ．[0°，90°)B ．[90°，180°)C ．(90°，180°)D ．(0°，180°) 变式2：设直线l 过原点，其倾斜角为α，将直线l 绕坐标原点沿逆时针方向旋转45°，得到直线l 1，则直线l 1的倾斜角为( )A ．α＋45°B ．α－135°C ．135°－αD ．当0°≤α＜135°时为α＋45°，当135°≤α＜180°时为α－135° 题型二、直线的斜率例2：(1)已知过两点A (4，y )，B (2，－3)的直线的倾斜角为135°，则y ＝________；(2)过点P (－2，m )，Q (m,4)的直线的斜率为1，则m 的值为________；(3)已知过A (3,1)，B (m ，－2)的直线的斜率为1，则m 的值为________．变式1：若直线过点 (1,2)，(4，2＋3)，则此直线的倾斜角是( )A ．30°B ．45°C ．60°D ．90°变式2：已知过两点)3,2(22-+m m A ，)2,3(2m m m B --的直线l 的倾斜角为045，则m = . 变式3：已知三点A (a,2)，B (3,7)，C (－2，－9a )在同一条直线上，实数a 的值为________． 变式4：已知A (m ，－m ＋3)，B (2，m －1)，C (－1,4)，直线AC 的斜率等于直线BC 的斜率的3倍，则m = ．题型三、直线的斜率的应用例3:在平面直角坐标系中，画出经过原点且斜率为1,-1,2及-3直线1l ，2l ，3l 及4l .例4:如图直线l 1，l 2，l 3，l 4的斜率分别为k 1，k 2，k 3，k 4，比较斜率的大小关系变式1：已知点A （-2,3）、B （3,2），过点P （0,-2）的直线l 与线段AB 有公共点，试求直线l 的斜率的取值范围。

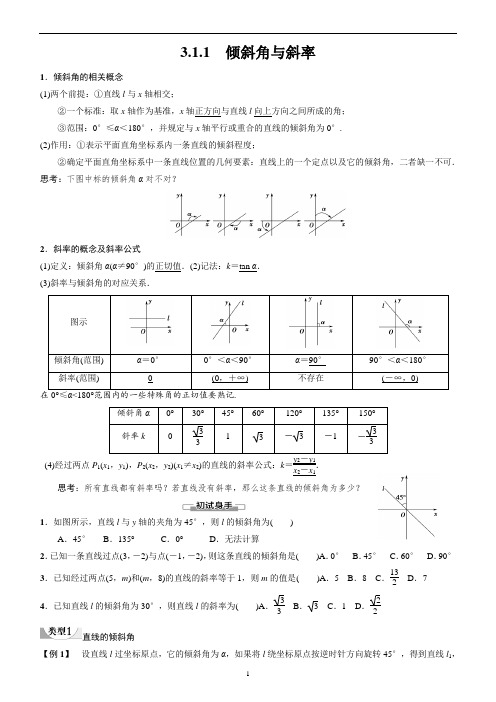
3.1.1 倾斜角与斜率1．倾斜角的相关概念(1)两个前提：①直线l 与x 轴相交；②一个标准：取x 轴作为基准，x 轴正方向与直线l 向上方向之间所成的角； ③范围：0°≤α＜180°，并规定与x 轴平行或重合的直线的倾斜角为0°. (2)作用：①表示平面直角坐标系内一条直线的倾斜程度；②确定平面直角坐标系中一条直线位置的几何要素：直线上的一个定点以及它的倾斜角，二者缺一不可． 思考：下图中标的倾斜角α对不对？2．斜率的概念及斜率公式(1)定义：倾斜角α(α≠90°)的正切值．(2)记法：k ＝tan α． (3)斜率与倾斜角的对应关系．图示倾斜角(范围) α＝0° 0°＜α＜90° α＝90° 90°＜α＜180° 斜率(范围)(0，＋∞)不存在(－∞，0)在0°≤α<180°范围内的一些特殊角的正切值要熟记.倾斜角α 0° 30° 45° 60° 120° 135° 150° 斜率k3313－3－1－33(4)经过两点P 1(x 1，y 1)，P 2(x 2，y 2)(x 1≠x 2)的直线的斜率公式：k ＝y 2－y 1x 2－x 1．思考：所有直线都有斜率吗？若直线没有斜率，那么这条直线的倾斜角为多少？1．如图所示，直线l 与y 轴的夹角为45°，则l 的倾斜角为( )A ．45°B ．135°C ．0°D ．无法计算2．已知一条直线过点(3，－2)与点(－1，－2)，则这条直线的倾斜角是( )A ．0° B ．45° C ．60° D ．90° 3．已知经过两点(5，m )和(m ，8)的直线的斜率等于1，则m 的值是( )A ．5 B ．8 C ．132 D ．74．已知直线l 的倾斜角为30°，则直线l 的斜率为( )A ．33 B ． 3 C ．1 D ．22直线的倾斜角【例1】 设直线l 过坐标原点，它的倾斜角为α，如果将l 绕坐标原点按逆时针方向旋转45°，得到直线l 1，那么l 1的倾斜角为( )A ．α＋45°B ．α－135°C ．135°－αD ．当0°≤α<135°时，倾斜角为α＋45°；当135°≤α<180°时，倾角为α－135°求直线的倾斜角的方法及两点注意(1)方法：结合图形，利用特殊三角形(如直角三角形)求角．(2)两点注意：①当直线与x 轴平行或重合时，倾斜角为0°，当直线与x 轴垂直时，倾斜角为90°. ②注意直线倾斜角的取值范围是0°≤α＜180°.1．一条直线l 与x 轴相交，其向上的方向与y 轴正方向所成的角为α(0°<α<90°)，则其倾斜角为( )A ．αB ．180°－αC ．180°－α或90°－αD ．90°＋α或90°－α 跟踪训练2 已知直线l 向上方向与y 轴正向所成的角为30°，则直线l 的倾斜角为 ．直线的斜率【例2】 (1)已知点A 的坐标为(3，4)，在坐标轴上有一点B ，若k AB ＝4，则点B 的坐标为( )A ．(2，0)或(0，－4)B ．(2，0)或(0，－8)C ．(2，0)D ．(0，－8) (2)已知直线l 经过点A (1，2)，且不经过第四象限，则直线l 的斜率k 的取值范围是( )A ．(－1，0]B ．[0，1]C ．[1，2]D ．[0，2]例3 经过下列两点的直线的斜率是否存在？如果存在，求其斜率，并确定直线的倾斜角α. (1)A (2,3)，B (4,5)； (2)C (－2,3)，D (2，－1)； (3)P (－3,1)，Q (－3,10)．解决斜率问题的方法(1)由倾斜角(或范围)求斜率(或范围)利用定义式k ＝tan α(α≠90°)解决． (2)由两点坐标求斜率运用两点斜率公式k ＝y 2－y 1x 2－x 1(x 1≠x 2)求解．(3)涉及直线与线段有交点问题常利用数形结合列公式求解．1．(1)已知过两点A (4，y )，B (2，－3)的直线的倾斜角为135°，则y ＝________．(2)过点P (－2，m )，Q (m ，4)的直线的斜率为1，则m 的值为________．跟踪训练2 如图所示，直线l 1，l 2，l 3都经过点P (3,2)，又l 1，l 2，l 3分别经过点Q 1(－2，－1)，Q 2(4，－2)，Q 3(－3,2)，计算直线l 1，l 2，l 3的斜率，并判断这些直线的倾斜角是锐角还是钝角．直线倾斜角与斜率的综合[探究问题]1．斜率公式k＝y2－y1x2－x1中，分子与分母的顺序是否可以互换？y1与y2，x1与x2的顺序呢？2．斜率的正负与倾斜角范围有什么联系？命题角度1三点共线问题例3如果三点A(2,1)，B(－2，m)，C(6,8)在同一条直线上，求m的值．跟踪训练3已知倾斜角为90°的直线经过点A(2m,3)，B(2，－1)，则m的值为()A．0 B．1 C．2 D．3命题角度2数形结合法求倾斜角或斜率范围例4直线l过点P(1,0)，且与以A(2,1)，B(0，3)为端点的线段有公共点，求直线l的斜率和倾斜角的范围．【例3】已知两点A(－3，4)，B(3，2)，过点P(1，0)的直线l与线段AB有公共点．(1)求直线l的斜率k的取值范围；(2)求直线l的倾斜角α的取值范围．将本例变为：已知A(3，3)，B(－4，2)，C(0，－2)．若点D在线段BC上(包括端点)移动，求直线AD的斜率的变化范围．1．求直线斜率的取值范围时，通常先结合图形找出倾斜角的范围，再得到斜率的范围．2．利用斜率可解决点共线问题，点A，B，C共线⇔k AB＝k AC或k AB与k AC都不存在．3.y2－y1x2－x1的几何意义是直线的斜率，用之可通过几何方法解决函数的值域问题．一、选择题1．下列说法中正确的是( )A ．一条直线和x 轴的正方向所成的正角，叫做这条直线的倾斜角B ．直线的倾斜角α的取值范围是[0°，180°]C ．和x 轴平行的直线的倾斜角为180°D ．每一条直线都存在倾斜角，但并非每一条直线都存在斜率 2．已知l 1⊥l 2，直线l 1的倾斜角为60°，则直线l 2的倾斜角为( ) A ．60° B ．120° C ．30° D ．150°3．若直线过坐标平面内两点(1,2)，(4,2＋3)，则此直线的倾斜角是( ) A ．30° B ．45° C ．60° D ．90°4．已知直线l 的斜率的绝对值等于3，则直线l 的倾斜角为( ) A ．60° B ．30° C ．60°或120° D ．30°或150° 5．下列各组中，三点能构成三角形的三个顶点的为( )A ．(1,3)、(5,7)、(10,12)B ．(－1,4)、(2,1)、(－2,5)C ．(0,2)、(2,5)、(3,7)D ．(1，－1)、(3,3)、(5,7) 6.若图中直线l 1、l 2、l 3的斜率分别为k 1、k 2、k 3，则( ) A ．k 1<k 2<k 3 B ．k 3<k 1<k 2 C ．k 3<k 2<k 1 D ．k 1<k 3<k 27．一条直线l 与x 轴相交，其向上的方向与y 轴正方向所成的角为α(0°<α<90°)，则其倾斜角为( ) A ．α B ．180°－α C ．180°－α或90°－α D ．90°＋α或90°－α 8．已知直线l 过点A (1,2)，且不过第四象限，则直线l 的斜率k 的最大值是( ) A ．2 B ．1 C.12 D ．0二、填空题9．若三点A (2,2)，B (a,0)，C (0，b )(ab ≠0)共线，则1a ＋1b的值等于 ．10．已知点A (1,2)，若在坐标轴上有一点P ，使直线P A 的倾斜角为135°，则点P 的坐标为 ． 11．若经过点A (1－t,1＋t )和点B (3,2t )的直线的倾斜角为钝角，则实数t 的取值范围是 ． 12．若直线l 经过A (2,1)，B (1，m 2)(m ∈R )两点，则直线l 的倾斜角的取值范围为 ． 三、解答题13．已知坐标平面内两点M (m ＋3,2m ＋5)，N (m －2,1)．(1)当m 为何值时，直线MN 的倾斜角为锐角？(2)当m 为何值时，直线MN 的倾斜角为钝角？ (3)直线MN 的倾斜角可能为直角吗？四、探究与拓展14．已知坐标平面内三点A(－1,1)，B(1,1)，C(2，3＋1)．若D为△ABC的边AB上一动点，则直线CD的斜率k的取值范围为()A．[33，3] B．[0，33]∪[3，＋∞) C．[33，＋∞) D．[3，＋∞)15．已知坐标平面内三点P(3，－1)，M(6,2)，N(－3，3)，直线l过点P.若直线l与线段MN相交，求直线l的倾斜角的取值范围．3.1.2两条直线平行与垂直的判定1．两条直线平行与斜率之间的关系类型斜率存在斜率不存在条件α1＝α2≠90°α1＝α2＝90°对应关系l1∥l2⇔k1＝k2l1∥l2⇔两直线斜率都不存在图示思考1如图，设对于两条不重合的直线l1与l2，其倾斜角分别为α1与α2，斜率分别为k1与k2，若l1∥l2，α1与α2之间有什么关系？k1与k2之间有什么关系？思考2对于两条不重合的直线l1与l2，若k1＝k2，是否一定有l1∥l2？为什么？2．两条直线垂直与斜率之间的关系图示对应关系l1⊥l2(两条直线的斜率都存在，且都不为零)⇔k1k2＝－1l1的斜率不存在，l2的斜率为0⇒l1⊥l2思考1如图，设直线l1与l2的倾斜角分别为α1与α2，斜率分别为k1与k2，且α1<α2，若l1⊥l2，α1与α2之间有什么关系？为什么？思考2 已知tan(90°＋α)＝－1tan α，据此，如何推出思考1中两直线的斜率k 1、k 2之间的关系？思考3 如果两直线的斜率存在且满足k 1·k 2＝－1，是否一定有l 1⊥l 2？如果l 1⊥l 2，一定有k 1·k 2＝－1吗？为什么？1．已知A (2，0)，B (3，3)，直线l ∥AB ，则直线l 的斜率k 等于( )A ．－3 B ．3 C ．－13 D ．132．已知直线l 1的斜率k 1＝2，直线l 2的斜率k 2＝－12，则l 1与l 2( )A ．平行B ．垂直C ．重合D ．非以上情况3．l 1过点A (m ，1)，B (－3，4)，l 2过点C (0，2)，D (1，1)，且l 1∥l 2，则m ＝________．两直线平行的判定及应用【例1】 根据下列给定的条件，判断直线l 1与直线l 2是否平行．(1)l 1经过点A (2，1)，B (－3，5)，l 2经过点C (3，－3)，D (8，－7)； (2)l 1经过点E (0，1)，F (－2，－1)，l 2经过点G (3，4)，H (2，3)； (3)l 1的倾斜角为60°，l 2经过点M (1，3)，N (－2，－23)； (4)l 1平行于y 轴，l 2经过点P (0，－2)，Q (0，5)．1．已知l 1经过点A (－3，3)，B (－8，6)，l 2经过点M ⎝⎛⎭⎫－212，6，N ⎝⎛⎭⎫92，－3，求证：l 1∥l 2.跟踪训练2 已知A (1，－a ＋13)，B (0，－13)，C (2－2a,1)，D (－a,0)四点，当a 为何值时，直线AB 和直线CD平行．两条直线垂直关系的判定【例2】 判断下列各题中l 1与l 2是否垂直．(1)l 1经过点A (－1，－2)，B (1，2)；l 2经过点M (－2，－1)，N (2，1)； (2)l 1的斜率为－10；l 2经过点A (10，2)，B (20，3)；(3)l 1经过点A (3，4)，B (3，10)；l 2经过点M (－10，40)，N (10，40)．例3已知三点A(5，－1)，B(1,1)，C(2,3)．求证：△ABC是直角三角形．使用斜率公式判定两直线垂直的步骤(1)一看：就是看所给两点的横坐标是否相等．若相等，则直线的斜率不存在；若不相等，则进行第二步．(2)二代：就是将点的坐标代入斜率公式．(3)求值：计算斜率的值，进行判断，尤其是点的坐标中含有参数时，应用斜率公式对参数进行讨论．1．已知直线l1经过点A(3，a)，B(a－1，2)，直线l2经过点C(1，2)，D(－2，a＋2)．若l1⊥l2，求a的值．跟踪训练2已知定点A(－1,3)，B(4,2)，以A，B为直径作圆，与x轴有交点C，求交点C的坐标．两直线平行与垂直的综合应用[探究问题]1．已知△ABC的三个顶点坐标A(5，－1)，B(1，1)，C(2，3)，你能判断△ABC的形状吗？2．已知定点A(－1，3)，B(4，2)，以AB为直径作圆，若圆与x轴有交点C.如何确定点C的坐标？【例3】△ABC的顶点A(5，－1)，B(1，1)，C(2，m)，若△ABC是以点A为直角顶点的直角三角形，求m 的值．1．本例中若改为∠A为锐角，其他条件不变，如何求解m的值？2．若将本例中的条件“点A为直角顶点”去掉，改为若△ABC为直角三角形，如何求解m的值？例4已知四边形ABCD的顶点B(6，－1)，C(5,2)，D(1,2)．若四边形ABCD为直角梯形，求A点坐标．引申探究本例中若将条件“四边形ABCD 为直角梯形”改为AC ∥BD ，AB ∥CD ，求A 点坐标．反思与感悟 有关两条直线垂直与平行的综合问题，一般是根据已知条件列方程(组)求解．如果涉及到有关四边形已知三个顶点求另外一个顶点，注意判断图形是否唯一，以防漏解．跟踪训练3 已知矩形ABCD 的三个顶点的坐标分别为A (0,1)，B (1,0)，C (3,2)，求第四个顶点D 的坐标．一、选择题1．设点P (－4,2)，Q (6，－4)，R (12,6)，S (2,12)，下面四个结论：①PQ ∥SR ；②PQ ⊥PS ；③PS ∥QS ；④PR ⊥QS . 其中正确的个数是( ) A ．1 B ．2 C ．3D ．42．如果直线l 1的斜率为a ，l 1⊥l 2，那么直线l 2的斜率为( ) A.1a B ．a C ．－1aD ．－1a或不存在3．若直线l 1的倾斜角为135°，直线l 2经过点P (－2，－1)，Q (3，－6)，则直线l 1与l 2的位置关系是( ) A ．垂直 B ．平行 C ．重合 D ．平行或重合4．已知点A (m,3)，B (2m ，m ＋4)，C (m ＋1,2)，D (1,0)，且直线AB 与直线CD 平行，则m 的值为( ) A ．1 B ．0 C ．0或1D ．0或25．已知直线l 的倾斜角为20°，直线l 1∥l ，直线l 2⊥l ，则直线l 1与l 2的倾斜角分别是( ) A ．20°，110° B ．70°，70° C ．20°，20°D ．110°，20°6．顺次连接A (－4,3)，B (2,5)，C (6,3)，D (－3,0)所构成的图形是( ) A ．平行四边形 B ．直角梯形 C ．等腰梯形 D ．以上都不对 二、填空题7．已知直线l 1经过点A (0，－1)和点B (4a ，1)，直线l 2经过点M (1,1)和点N (0，－2)，若l 1与l 2没有公共点，则实数a 的值为________．8．已知A (2,0)，B (3，3)，直线l ∥AB ，则直线l 的倾斜角为________．9．若点P (a ，b )与点Q (b －1，a ＋1)关于直线l 对称，则直线l 的倾斜角α为________．10．直线l 1，l 2的斜率k 1，k 2是关于k 的方程2k 2－3k －b ＝0的两根，若l 1⊥l 2，则b ＝____________；若l 1∥l 2，则b ＝____________.11．已知点A (－3，－2)，B (6,1)，点P 在y 轴上，且∠BAP ＝90°，则点P 的坐标是______．三、解答题12．当m为何值时，过两点A(1,1)，B(2m2＋1，m－2)的直线：(1)倾斜角为135°；(2)与过两点(3,2)，(0，－7)的直线垂直；(3)与过两点(2，－3)，(－4,9)的直线平行．四、探究与拓展13．已知P(－2，m)，Q(m,4)，M(m＋2,3)，N(1,1)，若直线PQ∥直线MN，则m的值为______．14．已知△ABC的顶点A(1,3)，B(－1，－1)，C(2,1)，求△ABC的边BC上的高AD的斜率和垂足D的坐标．。

直线的倾斜角与斜率杨兵一、教材分析1．教材的地位直线倾斜角和斜率是解析几何的重要概念之一，是刻画直线倾斜程度的几何要素与代数表示，是在平面直角坐标系内以坐标法〔解析法〕的方式来研究直线及其几何性质的根底。

本课有着开启全章，承前启后，奠定基调，渗透方法的作用。

2．教学目标知识与技能：理解直线的倾斜角和斜率的定义，掌握过两点的直线的斜率计算公式。

过程与方法：引导学生观察、探索、合作探究、发现，培养学生的探索创新能力和合作意识。

情感、态度与价值观：通过学生之间、师生之间的交流合作，实现共同探究的目标。

并体验认识事物的一般规律：从特殊到一般的过程。

二、教学重点、难点重点：直线的倾斜角、斜率的概念和公式；难点：对直线倾斜角以及斜率的理解；三、教学过程1．创设情景，形成概念问题1：过一点能确定一条直线吗？问题2：这些直线有怎样的区别？怎样准确的表示它们的区别呢？2.〔1〕直线倾斜角的定义：直线与x 轴相交时，直线向上的方向与x 轴正方向所成的角 叫做这条直线的倾斜角．(2)直线倾斜角的范围：0︒≤α<180︒【设计意图】让学生了解到除了两点能确定一条直线的位置外，一个点和方向也能确定一条直线的位置。

学生了解倾斜角的概念，并发现倾斜角的取值范围3．发现问题，探索新知通过上面的学习，我们知道倾斜角可以刻画直线的倾斜程度，那么我们在还学习过什么量可以表达倾斜程度呢？斜率的定义：一条直线的倾斜角α的正切值叫做这条直线的斜率(slope)，常用小写字母k表示；α=ktan【设计意图】通过这个问题让学生意识到可以用角的正切值来表示坡度，从而让学生理解：用倾斜角的正切值来表示直线的倾斜程度，也就是斜率。

4.深入探究，加深理解〔1〕发现直线斜率随着倾斜角的变化会怎么样变化。

是不是每条直线都有斜率？倾斜角不同，斜率是否相同？〔2〕由正切函数的图像，引导学生得到倾斜角与斜率的图像。

进一步探究斜率k和倾斜角α的关系请根据斜率k和倾斜角α的关系完成以下填空：〔3〕应用探究在平面直角坐标系中，画出经过原点且斜率分别为1，-1的直线，【设计意图】及时稳固斜率k和倾斜角α的关系式，进一步明确确定一条直线的两个几何要素：点和倾斜角。

3.1.1直线的倾斜角和斜率（1）一、教学目标知道一次函数的图象是直线，了解直线方程的概念，掌握直线的倾斜角和斜率的概念以及直线的斜率公式．二、重难点1．重点：通过对一次函数的研究，学生对直线的方程已有所了解，要对进一步研究直线方程的内容进行介绍，以激发学生学习这一部分知识的兴趣；直线的倾斜角和斜率是反映直线相对于x轴正方向的倾斜程度的，是研究两条直线位置关系的重要依据，要正确理解概念；斜率公式要在熟练运用上多下功夫．2．难点：一次函数与其图象的对应关系、直线方程与直线的对应关系是难点．由于以后还要专门研究曲线与方程，对这一点只需一般介绍就可以了．三、教学过程(一)复习一次函数及其图象已知一次函数y=2x+1，试判断点A(1，2)和点B(2，1)是否在函数图象上．初中我们是这样解答的：∵A(1，2)的坐标满足函数式，∴点A在函数图象上．∵B(2，1)的坐标不满足函数式，∴点B不在函数图象上．现在我们问：这样解答的理论依据是什么？(这个问题是本课的难点，要给足够的时间让学生思考、体会．)讨论作答：判断点A在函数图象上的理论依据是：满足函数关系式的点都在函数的图象上；判断点B不在函数图象上的理论依据是：函数图象上的点的坐标应满足函数关系式．简言之，就是函数图象上的点与满足函数式的有序数对具有一一对应关系．(二)直线的倾斜角一条直线l向上的方向与x轴的正方向所成的最小正角，叫做这条直线的倾斜角，如图中的α．特别地，当直线l和x轴平行时，我们规定它的倾斜角为0°，因此，倾斜角的取值范围是0°≤α＜180°．点：(1)以x轴正向作为参考方向(始边)；(2)直线向上的方向作为终边；(3)最小正角．(三)直线的斜率倾斜角不是90°的直线．它的倾斜角的正切叫做这条直线的斜率．直线的斜率常用k表示，即αk=tan(四)过两点的直线的斜率公式在坐标平面上，已知两点P1(x1，y1)、P2(x2，y2)，由于两点可以确定一条直线，直线P1P2就是确定的．当x1≠x2时，直线的倾角不等于90°时，这条直线的斜率也是确定的．怎样用P2和P1的坐标来表示这条直线的斜率？P2分别向x 轴作垂线P1M1、P2M2，再作P1Q ⊥P2M ，垂足分别是M1、M2、Q ．那么： α=∠QP1P2(图甲)或α=π-∠P2P1Q(图乙)在图甲中：121212tan x x y y Q P QP --==α在图乙中：xx y y QP QP Q P P --==<-=2121212tan tan α如果P1P2向下时，用前面的结论课得：xx y y x x y y --=--=2122121tan α综上所述，我们得到经过点P1(x1，y1)、P2(x2，y2)两点的直线的斜率公式：对于上面的斜率公式要注意下面四点：(1)当x1=x2时，公式右边无意义，直线的斜率不存在，倾斜角为90°；(2)k 与P1、P2的顺序无关；(3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得；(4)求直线的倾斜角可由直线上两点的坐标先求斜率得到． (五)例题例1 如图，直线l1的倾斜角α1=30°，直线l2⊥l1，求l1、l2的斜率． 解： ∵l2的倾斜角α2=90°+30°=120°，3120tan 20-==∴k本例题是用来复习巩固直线的倾斜角和斜率以及它们之间的关系的，可由学生课堂练习，学生演板．例2 求经过A(-2，0)、B(-5，3)两点的直线的斜率和倾斜角．∴tgα=-1．∵0°≤α＜180°， ∴α=135°．3330tan 10==k因此，这条直线的斜率是-1，倾斜角是135°．讲此例题时，要进一步强调k与P1P2的顺序无关，直线的斜率和倾斜角可通过直线上的两点的坐标求得．(六)课后小结(1)直线的方程的倾斜角的概念．(2)直线的倾斜角和斜率的概念．(3)直线的斜率公式．三、布置作业1．在坐标平面上，画出下列方程的直线：(1)y=x(2)2x+3y=6(3)2x+3y+6=0(4)2x-3y+6=0作图要点：利用两点确定一条直线，找出方程的两个特解，以这两个特解为坐标描点连线即可．2．求经过下列每两个点的直线的斜率，若是特殊角则求出倾斜角：(1)C(10，8)，D(4，-4)；解：(1)k=2．(3)k=1，α=45°．3．已知：a、b、c是两两不相等的实数，求经过下列每两个点的直线的倾斜角：(1)A(a，c)，(b，c)；(2)C(a，b)，D(a，c)；(3)P(b，b+c)，Q(a，c+a)．解：(1)α=0°；(2)α=90°；(3)α=45°．4．已知三点A(a，2)、B(3，7)、C(-2，-9a)在一条直线上，求实数a的值．∵A、B、C三点在一条直线上，∴kAB=kAC．六、板书设计3.1.1直线的倾斜角和斜率（2）一、教学目标(一)知识教学点复习直线的倾斜角和斜率的概念以及直线的斜率公式．(二)能力训练点通过对知识点的应用（例题1、例题2及课堂练习），巩固学生所学的知识，培养学生分析、解决问题的能力；．(三)学科渗透点分析问题、提出问题的思维品质，事物之间相互联系、互相转化的辩证唯物主义思想． 二、教材分析1．重点：通过上一节课的学习，学生对直线的倾斜角和斜率的求法已有所了解，直线的倾斜角和斜率是反映直线相对于x 轴正方向的倾斜程度的，是研究两条直线位置关系的重要依据，要正确理解概。