当前位置：文档之家 › 大学物理课件第三章 动量与角动量

大学物理课件第三章 动量与角动量

  • 格式：ppt
  • 大小：499.00 KB
  • 文档页数：31

下载文档原格式

  / 31

合集下载

大学物理课件 第3章 动量 角动量

大学物理课件 第3章 动量 角动量

例 如图所示,一个有四分之一圆弧光滑槽的大物体,质量为 M, 置于 光滑的水平面上。另一质量为m的小物体从圆弧顶点由静止开始下滑。 求当小物体m滑到底时，M滑槽在水平上移动的距离。
解 以 M和 m 为研究对象，其在水平方向不受外力（所受外力都 在竖直方向），故水平方向动量守恒。
设在下滑过程中，m相对于M的滑动速度为m ， M 对地速 度为 M ，并以水平方向右为正，则有
t
问题 结果与m与槽M间是否存在摩擦有关系吗？
3. 质心运动定理
C
mii mc m i 1 质点系的动量 p mc
i 1
m
n
rC
mi ri
n i 1
m
n
i i
质点系的动量等于质点系的质量乘以质心的速度。 注 质点系的动量的两种表达式
n p mii , p mc
pA m j ,
pB mi
y
B
I AB pB pA m (i j )
C
pC m j
o
A
x
I AC pC pA 2m j
质点的动量定理
例 一质量为10kg的物体沿x轴无摩擦地运动，设t=0时，物体 位于原点，速度为零。设物体在力(F=3+4t)N作用下运动了3秒， 求此时它的速度和加速度。 解
3.2
角动量定理 角动量守恒定律
3.2.1 质点的角动量定理及守恒定律
1. 力矩
讨论
力F 对定点O 的力矩 Mo F r F
单位：牛 米（N m）
(1)力矩的大小和方向
所组成的平面，指向是由 180 的角转到 F 时的右手螺旋前进的方向
①方向垂直于 r 和 F o
r 经小于
x 方向： m sin m0 sin 0 y 方向： ( f mg )t m cos m0 cos sin 由第一式 0 sin

第三章动量与角动量.ppt

第三章动量与角动量.ppt

● 讨论：
1）质点系动量定理微分形式
F mac
t2
F外dt P P0
(F dP ) dt
积分形式
t1
2) 质心处的质点（质点系总质量）代替质点系整体的平动
3）若 F 0 vc不变
质心速度不变就是动量守恒（同义语）
4) F mac
意义：质心的加速度决定于质点系所受的合外力.
牛顿第二定律的最初表达式 F dp d(mv) dt dt
冲量: 力的时间积累
过程量. 方向：速度变化的方向；单位：Ns ;
变力的冲量 I FiΔti
i
若力连续变化 I t2 Fdt t1
动量: p＝mv （状态量, 矢量）
大小：mv 单位：kgm/s
方向：速度的方向
二、质点的动量定理 (theorem of momemtum)
设物体受外力 F , 考虑 dt 时间内力的积累:
由 F dp dt
Fdt dp (微分形式)
对上式积分得 t2-t1 时间内力的积累：
t2 F (t)dt t1
p2 dp
p1
p2

p1
动量定理
I
t2 F (t )dt
t1

p2

p1
(积分形式)
合外力对质点在一段时间内的冲量等于此过程始末状态质 点动量的增量.
以火箭本身作为研究对象，以F表示喷出气体对火箭的推力， 则由牛顿第二定律，有
F M dv dt
Mdv udM udm
F

dm u
dt
可见火箭发动机的推力与燃料燃烧速率及 喷出气体的相对速度成正比.

3-动量与角动量.ppt

3-动量与角动量.ppt

y
h
o
l
x
dm dS (l x )h d S y d x (l x ) ta n d x dx l M S lh / 2
y
y
h
xc
M l2 hl2 h 2 1 2 3 xc l l l M 3 3
xdm
0
l
v2
v1
60o
因打击力很大，所以由碰撞引起的质点的动 量改变，基本上由打击力的冲量决定。 重力、阻
力的冲量可以忽略。
mv2
60o
mg t
mv1
打击力冲量 F t
F t m v m v 2 1
F t m v m v
2 1
F t
30o 60o m=140g
o
rc
【思考】写出上式的分量形式
x y z
c


N
m m
N
i 1
i
x
i
c


m m
N
i 1
i
y
利用分量形式很容 易求得一些几何形 状对称和结构均匀 物体的质心位矢，
i
m m
c

i 1
i
z
i
例如：均匀直棒、 均匀圆盘、均匀球 体等 其质心就在几何对 称中心上
fi
m
i
由N个质点构成的系统
i ,j 1 , 2 , , N
ri
1、内力和外力
fji 内力： fij 外力：fi , fj
惯性系 o
rj
fij f ji m j

3 动量和角动量-PPT精品文档

3 动量和角动量-PPT精品文档
i
xc

i 1
xi m i m

xdm
m
m
质心位矢与坐标系建立有关，但质心相对质点系内质点的相 对位置不变。
xdm ydm zdm 质量连续 x y z 分布时： dm dm dm
c c c
dm为质量元，简称质元。其计算方法如下： 质量为线分布 dm dl 其中、、分 别为质量的线密 质量为面分布 dm ds 度、面密度和体 质量为体分布 dm dV密度。
p
i
ix
const .
4. 比牛顿定律更普遍的最基本的定律。
§3.4 质心
N个粒子系统，可定义质量中心
z
rc

N
i1i
mi



N
i1
m i ri m
i i
i1
xc
y
m x
i
i
x
对连续分布的物质
yc
zc
m mi yi
m mi z i
r c
即
miri
i
m
xc
mx
i i
i
m
0
m
m x M X 0
mR X (M m)
x x X而 x R
M
x
例3.3：水平桌面上拉动纸，纸张上有一均匀球，球的质量M， 纸被拉动时与球的摩擦力为 F，求：t 秒后球相对桌面 移动多少距离？ y 解：
的角动量？
M
o
r
F

L
p
r

o
方向用右手螺旋法规定
M r F

大学物理教学资料——动量与角动量-PPT课件

大学物理教学资料——动量与角动量-PPT课件
m2 gh N mg t
y
N
1200 N t 1 s 时 , N 600 600 t 0 . 1 s 时 , N 600 6000 6600 N
m g
例：一枚静止的炸弹在水平面内爆炸，炸成三块，第 一块质量为m,速度v1=800m/s，向西；第二块质量为 m，速度v2=600m/s,向南；第三块质量为2m，求：第 三块弹片的速度大小和方向。
元冲量 元增量
若力作用了 t2 - t1一段时间,则有
t 1 2
t 2 I F d t p p t ot al 1
合力的冲量 （过程量） 动量增量 （始末状态量）
动量定理 （积分形式）
三、求冲量的两种方法
t2 是变力，不能轻易地移到积分外。 （1）I Fdt F
t1
I x Fxdt
t2
对 F 矢量积分，把 F 分成三个分量。
p1
I y Fy dt
IZ Fz dt
t1
t1
I
p2
t2
t1 t2
z
p1
t2
F t
P P （2）I 2 1
2 2 2 I Ix Iy Iz
x
0 t1
y
一个过程量等于始末两个状态量之差。 冲量是矢量, 冲量的方向一般不同于初、 末 动量的方向，而是动量 增量的方向。


记作
质点系动量定理 F d t d P 外
（微分形式）
F d t d P 外
质点系动量定理 或 d t P P 外 2 1 （积分形式） F
t2 t 1
“质点系总动量的增量等于该质点系所受的 合外力的冲量” 注意:内力不影响质点系的总动量！ 但内力可影响质点系内某些质点的动量。 质点系动量定理是牛III的必然推论。

动量和角动量课件

动量和角动量课件

角动量守恒定律与物理世界的应用
角动量守恒定律可解释陀螺的稳定性和星体自 转的变化。
总结1 动量和角动量的重源自性动量和角动量是描述物体运动和转动的基本 概念。
2 动量定理和角动量定理的相互关系
动量定理和角动量定理都涉及力对物体的影 响和改变。
3 冲量和角冲量的应用
冲量和角冲量可用于描述碰撞和旋转过程中 的力的传递和改变。
动量和角动量
动量和角动量是物理学中重要的概念。本课件将介绍它们的定义、定理以及 与物理世界的应用，以及动量和角动量的重要性和守恒定律。
动量和角动量的概念
动量的定义
动量是物体运动过程中的物理量，其大小和速 度有关。
角动量的定义
角动量是物体绕某一旋转轴自旋运动时的物理 量，其大小和旋转速度、质量以及距离有关。
动量定理和角动量定理
动量定理的表述和应用
动量定理指出外力对物体的作用会改变物体的 动量，可以用于解释运动过程中的碰撞和推动 现象。
角动量定理的表述和应用
角动量定理指出外力矩对物体的作用会改变物 体的角动量，可以用于解释自旋和转动的现象。
冲量和角冲量
冲量的定义和计算
冲量是力在时间上的累积作用，可用于描述在碰撞中力的传递与改变情况。
角冲量的定义和计算
角冲量是力矩在时间上的累积作用，可用于描述旋转物体转动过程中力矩的传递与改变情况。
守恒量
动量守恒定律
动量守恒定律指出在孤立系统中，物体的总动 量保持不变。
角动量守恒定律
角动量守恒定律指出在没有外力矩作用下，物 体的总角动量保持不变。
延伸阅读
动量守恒定律与物理世界的应用
动量守恒定律可解释火箭推进原理和碰撞事故 中的能量守恒。
4 守恒量的重要性和应用

第3章动量与角动量.ppt

第3章动量与角动量.ppt

udM

0
( dm dM ) 质量比

v
M
dv u
dM
v0
M0 M
v v0
u ln
M0 M
u ln N
提高火箭速度的途径有二：
对应的措施是：
第一条是提高火箭喷气速度u
选优质燃料
第二条是加大火箭质量比
采取多级火箭
M0/终M速度为：v u1 ln N1 u2 ln N2 u3 ln N3
角动量定理
r M

v dL
dt
质点所受合外力矩 = 质点角动量对时间的变化率
r M
和
Lv都是相对惯性系中同一定点定义的。
积分形式：
t2 t1
M
dt

L2

L1
t2 Mdt —冲量矩，力矩的时间积累。
t1
§3.7 角动量守恒定律
M

0

L
常矢量
若对惯性系某一固定点，质点所受的合外力矩为零，则 此质点对该固定点的角动量矢量保持不变，即角动量的大小 和方向都保持不变。

m
rv
r sin

2m
1 2
rv
r sin

2m
S

const
t
t
t
所以，面速度为常数
讨论
1）角动量守恒定律的条件 M 0
2）动量守恒与角动量守恒是相互独立的定律 动量不守恒
如行星运动 角动量守恒
3）有心力: 力始终过某一点。
M 0 角动量守恒
o
F

行星在速度和有心力所组成的平面内运动

大学物理课件-第3章 动量与角动量(momentum and angular momentum)-文档资料

大学物理课件-第3章 动量与角动量(momentum and angular momentum)-文档资料

v2i7(m)/s
鞍山科技大学 姜丽娜
12
例2
一质量为 m 的物体,原来向北运动,速率为vo ,它突然受到外力的打击,
变为向东运动,速率为 3 v o 。求打击过程外力的冲量大小和方向。
解:

p1m v 1mojv
p2m v23moiv
Y mv1
p
mv2
o
X
根据动量定理忽略 重力的冲量,则外力的冲 量为 I pp 2p 13moiv mojv
n
上面各式相加得
n
n d Pi来自 fi fij
i1
i1, j1,ij
i1
dt
n
n d Pi
fi
i 1
id鞍1t山科技—大学—姜质丽娜点系动量定理的微分式8
质点系动量定理的积分式
n
t2 n
Pi 2
i1
n
n n
I ( fi )dt d( Pi ) Pi2 Pi1
解:
(1)研究对象： t 时刻车中煤 的总质量m和 t+dt 时刻 落入车厢的煤 的质量dm
（t 时2）刻设和以t+d地t时面刻为系参统考水系平，总建动立量直分角别坐为标:系如v 图d，m
mvdm 0mv
m

m d v m v (m d m )v
F
dt时间内系统水平总动量增量为:
t1 i1
n i1 Pi1
i1
i1
i1 1
意义:
系统所合外力的冲量等于该系统动量的增量。
直角坐标系下的动量定理:
t2
t2

I f d t (fxi fy j fzk)dt IxiIyjIzk

大学物理课件-力学1.31.4动量和角动量

大学物理课件-力学1.31.4动量和角动量
一. 质点系 把相互作用的若干个质点看作为一个整体, 这组质 点就称为质点系. 二. 质点系的动量定理 内力: f1 , f 2 m1 m1 , m2 系统 : m2 f2 外力: F1 , F2 二式相加, 分别运用牛顿第二定律 : dP1 由于 f1 f 2 m1: F1 f1 dt d dP2 m2: F2 f 2 F1 F2 P1 P2 dt dt
1

t2
t1
Fdt
t2
Fdt
mv2 mv1
1）直角坐标系中的分量式( 二维 ):
I x t Fx dt P2 x P1 x
t2
2） 动量定理在碰撞问题中具有特殊重要的意义。 在碰撞过程中由于作用时间极短,作用力（冲力）却 很大. 并且随时间变化很难测定，但可借助始﹑末动 量变化和作用时间来计算平均冲力。
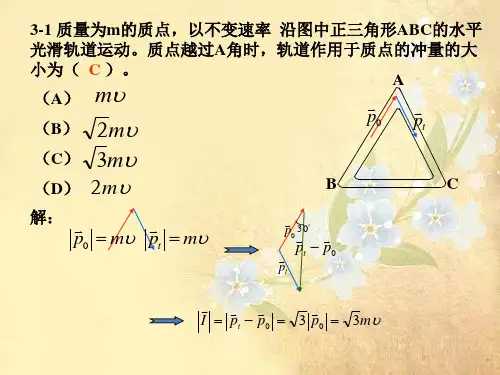
C
dl

dm =l dl .
l = m / (R)
R·dox源自由对称性可知, 质心C一定在 y 轴上, 即：xC=0 ,
yC
ydm
m

y l dl
m

l R sin Rd
0


R l

2

R
质心运动定理
(theorem of the motion of center of mass) 质点系的动量 N P mi v i
f1
F1
F2


对N个质点系统，外力用 F ，内力（即质点之间的 相互作用）用 f ，则第 i 及第 j 质点的运动方程
Fi
j i
dpi f ij dt

课件：第3章 动量与角动量

课件：第3章 动量与角动量

3-3 一质点做匀速率圆周运动时，（ C ）。 （A）它的动量不变，对圆心的角动量也不变； （B）它的动量不变，对圆心的角动量不断改变； （C）它的动量不断改变，对圆心的角动量不变； （D）它的动量不断改变，对圆心的角动量也不断改变。
解：略
3-4 如图所示，质量为m的小球自高为y0处沿水平方向以速
bt
。
（2）开始时，若B的动量为-p0，则pB2 =
-p0+bt
。
解：物体A和B这一系统的动量守恒。一维情况下用标量即可 pA pB Const
pB Const pA Const p0 bt
（1） 由题设，t 0, pB 0
Const p0
pB bt
（2） 由题设，t 0, pB p0
)(
m1 m1 m2
v)2
m1 m1 m2
(1 2
m1v2 )
3-7 两个相互作用的物体A和B，无摩擦地在一条水平直线上
运动。物体A的动量是时间的函数，表示式是pA = p0- bt，式 中，p0、b分别为正常数，t为时间。在下列两种情况下，写 出物体B的动量作为时间的函数表示式：
（1）开始时，若B静止，则pB1 =
（A）动能不变，动量改变； （B）动量不变，动能改变；
R O
（C）角动量不变，动量不变；
（D）角动量改变，动量改变；
（E）角动量不变，动能、动量都改变；
解：小物体只受重力、桌面对它的支持力及绳的拉力。前二者平 衡掉了，且这对力的作用点相同，故对小物体无力矩。绳的拉力 始终指向圆心，对小物体的力矩在任何时刻都为零。故，小物体 在运动过程中受的总力矩时时刻刻均为零，因而其角动量守恒； 拉力对小物体做了功，故由动能定理小物体的动能有改变；拉力 对时间的积分不为零，由动量定理，这一积分值恰为小物体动量 的增量，也即，小物体的动量有改变。

大学物理课件第3章 动量与角动量

大学物理课件第3章 动量与角动量

§3.3 动量守恒定律 质点系所受合外力为零， Σ 时间改变，即
Fi = 0 总动量不随
N P pi 常矢量
i 1
1. 合外力为零，或外力与内力相比小很多；
2. 合外力沿某一方向为零；
p i
i
const .
3. 只适用于惯性系； 4. 比牛顿定律更普遍的最基本的定律。
M r F
力
M F d F r sin
提问:力矩为0的情况?
力矩
Lrp
动量
N m 矢量性: r F
单位:
三、角动量定理
pr p v pr F Lr 角动量定理： r F M (力矩)
q
v
V
v sinq
v cosq V

解：设车相对地面的反冲速度为V，方向水平向左 炮弹相对地面的速度水平分量为 v cosq V mv cosq 水平方向动量守恒 m(v cosq V ) MV 0 解得V
炮弹相对地面的速度竖直分量为 v sinq
m M
v sinq tg v cosq V
t2
mg
3秒时物是否被拉起？
F cos f 0 N F sin mg 0 f N t1 1.9 s
I x 0.62 Kgm / s
t1
F
x
dt 1.12t (cos sin ) mg dt
3
I x mvx 0 0.62Kgm / s
6
h
v
0
N =
m 2gh
τ
m 工件
mg

第3章：动量与角动量.ppt

第3章：动量与角动量.ppt
解：以竖直悬挂的链条和 桌面上的链条为一系统，
m2
O
建立如图坐标，则：
F ex m1g yg
m1
y
由质点系动量定理得：
F exdt dp
y
F exdt dp
又 dp d(yv)
ygdt d(yv)
则
yg dyv
dt
两边同乘以 yd y 则：
y2gdy ydy dyv yv dyv
dt
g y y 2 d y yv yv dyv
0
0
m2
O
m1
y
y
1 gy3 1 yv2
32
v


2
gy
1 2
3
3.2 动量守恒定理
质点系动量定理：I t t0
Fiexdt
pi

pi0
动量守恒定律


若质点系所受的合外力为零：Fex Fiex 0
速率和角度弹回来。设碰撞时间为 0.05s。求此时间
内钢板所受到的平均F冲力 。
解：建立如图坐标系，由动量定理
Fxt mv2x mv1x
mvcos (mvcos)
x
mv1

2mv cos Fyt mv2y mv1y
m v2
mvsinα mvsin 0
p0 p

0 0
t2
t1
(F1

F12 )dt

m1v1

m1v10
t2
t1
(F2

F21 )dt

m2v2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
总动量保持不变。
即当 F Fi 0 时， P Pi＝恒矢量
i
i
此形式的定律只是适用惯性参照系。
动量守恒定律是自然界中一个基本守恒定律，只是
表现的形式不同。
质点的角动量： 角动量定理：
dL M dt
L r p
M r F
（其中 M 为对同一定点的合外力矩）
例题3
3、质量m=10g的子弹， 以速度 v 0 500m / s 沿水平方向
射穿一物体。穿出时，子弹的速率为v=30m/s，仍是水平 方向。则子弹在穿透过程中所受的冲量大小为 方向为 。 ，
解：根据题意，子弹在水平方向击中木块 由动量定理：
I mv mv0 4.7 N s
方向与子弹速度相反
I I F t F 15 N t
I Fdt (3 4t 2 )dt 45N s
t1 0
t2
3
I P mv3 mv0 v3 45m / s
例 题 11
11、质量m=10kg的木箱放在地面上，在水平拉力F的作用
下由静止开始沿直线运动，其拉力随时间的变化关系如图 所示。若已知木箱与地面间的摩擦系数 0.2 ，那么在 t=4s时木箱的速度；在t=6s时，木箱的速度。(g=10m/s2)
L m 3GMR
例 题 15
15、质量为0.05kg的小块物体，置于一光滑水平面上。有 一绳一端连接此物，另一端穿过桌面中心的小孔（如图 所示）。该物体原以ω 1= 3rad/s 的角速度在距孔0.2m的 圆周上转动。今将绳从小孔缓慢往下拉，使该物体之转半 径减为0.1m。则物体的角速度ω
i 6j
(B) 4i 6 j
(D) 3i 6 j
例题2
2、质量分别为 m A和 m B (m m ) 、速度分别为 A B
v A 和 v B的两质点A和B (v A v B ) ，受到相同的冲
量作用，则[ ]
(A) A的动量增量的绝对值比B 的小； (B) A的动量增量的绝对值比B 的大； (C) A、B 的动量增量相等； (D) A、B 的速度增量相等。
t1
质点系的动量定理： 系统的总动量增量等于该系统所受的合外力冲量。
即： 其中
t2 I F dt P2 P 1
t1
n F Fi i 1
n P Pi i 1
内力能使系统内各质点的动量发生变化，但对系统 的总动量没有影响。
动量守恒定律： 一个质点系所受的合外力为零时，这一质点系的
例 题 14
14、有一人造地球卫星，质量为m，在地球表面上空两
倍于地球半径R的高度沿圆轨道运行。用m、R、G和地
球质量M表示，求卫星运动的角动量大小。
解：角动量的定义式： L r mv
2
人造卫星做圆周运动，所以角动量大小 L mvr
GMm GMm mv GM F 2 v 2 r (3R) 3R 3R
上升时间 t 2
y ，解得 g
v y gt2 gy
根据动量定理分量式： I y mvy mvy 0 (1 2 )m gy （2）水平方向冲量
1 1 I x m v mv mv 2 2
大小为
例题6
6、一质量为m的物体，原来以速率v向北运动，它突然受到 外力打击，变为向西运动，速率仍为v，则(1)外力的冲量大 小为 ，方向为 。
例题4 4、A、B两木块质量分别为 m A 、m B， mB 2m A 。两
者用轻弹簧连接后静止于光滑水平桌面上，如图所示。
若用外力将两木块压近使弹簧被压缩，然后将外力撤
去，则此后两木块运动速度之比为[
(A)
]
1 2
2/2
(B)
(C)
mA
mB
2
2
(D)
例题5
5、质量为m的小球自高处
1 1 与地面碰撞后跳起的最大高度为 y 0 ，水平速率为 v 0 ， 2 2 y 则碰撞过程中
角动量守恒定律： 对于某一定点，质点（或质点系）受 的合外力矩为零时，则对此定点的角动量保持恒定。 即：
L 常矢量
例题1
1、一力 F 2ti 6 j 作用在一质点上，t 为时间，则 为 [ 从 t 1 到 t 2 这段时间的动量增量 p ].
(A) (C)
ij
2
=
v2
.
r2
演
示
v1
r1
o
m
F
解：根据题意， 物体转动过程中满足角动量守恒定律 有
m r m r
2 11
2 1 2 2
2 2 2
v2
r2 v1
r1
o
m
r 解得： 2 1 12rad / s r
F
例 题 16
16 、 我国第一颗人造卫星绕地球沿椭圆轨道运动，地 球的中心 O为该椭圆的一个焦点．已知地球的平均半径 R=6378 km，人造卫星距地面最近距离l1=439 km，最远
例 题 13
13、两球质量分别是 m1 20 103 kg, m2 50 103 kg ， （SI制）碰撞后合为一体，求碰撞后的速度？
在光滑桌面上运动，速度分别为 v1 10i , v2 3.0i 5.0 j
解：方法一，根据动量守恒定律
m1 v1 m2 v 2 (m1 m2 )v
(2)当物体以速度 v 始终沿某一直线作匀速运动时，该物体 对直线上任意一点的角动量为______________。
v
v
解：（1）根据题意设物体初速度为 v0 vj ，
受击打后的末速度为 v vi
则根据动量定理：
v
v
o
y
I P mv mv0 m(vi vj )
A
o
B
例题9
9、一个质量 m 0.14kg 的垒球沿水平方向以 v1 50m / s 的 速度投来，经棒打击后，沿仰角 450 的方向向回飞出， 速率变为 v 2 80m / s . （1）求棒给球的冲量的大小和方向？ （2）如果球与棒接触的时间为 t 0.02 s , 求棒对球的平均冲力的大小. （3）它是垒球本身重量的几倍?
（1） 地面对小球的竖直 冲量的大小为 ；
1 y0 2
0
y0 沿水平方向以速率 v0 抛出，
v0
（2） 地面对小球的水平
冲量的大小为 。
1 v0 2
x
解：（1）设碰撞前Y轴方向速度 v y 0 ， 碰撞后Y轴方向速度 v y 下落时间 t 1
2y ，解得 v y 0 g
gt1 2 gy
f t(N)
30
0
4
7
t(s)
解：（1）根据题意，木箱运动过程中始终受摩擦力 f t(N) f m g
30 N ft 70 10t
0t 4 4t 7
30
0
Ft f t f
当 t 4s 时 (2)当 t 6 s 时
4
7
t(s)
4m/s Ft t mv4 mv0 v4 8 m/ s
第三章 动量和角动量
一、教学基本要求:
本章主要介绍了质点和质点系的动量定理及角动量定 理，并重点讨论了质点系动量守恒定律的应用 1、掌握质点动量定理和动量守恒定律.
2、掌握运用守恒定律分析问题的思想和方法，能分
析简单系统在平面内运动的力学问题. 3、掌握质点在平面内做曲线运动时的角动量定理及 角动量守恒定律.
距离l2=2384 km．若人造卫星在近地点A1的速度v1=8.10
km/s，求人造卫星在远地点的速度v l2
A2
2
． l1 m
A1
解：因人造卫星所受引力指向地球中心，所以 M 0 ，
人造卫星的角动量守恒。
A1 : L1 mv1 ( R l1 ) A2 : L2 mv2 ( R l2 )
第三章 作业 教材:P32 例题2-7 学习指导：11 课件：9、10、12
期中考试:4月22日 下午 前四章
外力冲量大小为 I 2mv
x
方向沿西南方向 450
（2 ） 角动量的定义式： L r mv
所以角动量为零。
物体对运动直线上的任意一点的 r // v ，
例题7
7、一质点作匀速率圆周运动时[ ]
(A)它的动量不变，对圆心的角动量也不变; (B)它的动量不变，对圆心的角动量不断改变; (C)它的动量不断改变，对圆心的角动量不变;
A2
l2
l1 m
A1
mv1 ( R l1 ) mv2 ( R l2 )
v2 6.30km/s
R l1 v2 v1 R l2
教材 P32 例题 2-7
一质量为1kg的质点在变力F=6t（N） 作用下沿x轴运动，设t=0时，质点速度 v0=2m/s，质点位置x0=0m，试求质点在1s 末的速度和角动量也不断改变.
例题8
8、人造地球卫星绕地球作椭圆轨道运动，卫星轨道近地点
和远地点分别为A和B。用L和Ek分别表示卫星对地心的角 动量及其动能的瞬间值，则应有[ (A) L L , E E A B KA KB (B) L L , E E A B KA KB (C) L L , E E A B KA KB (D) LA LB , E KA E KB ]
解得：
25 v 5i j 7
方法二，利用动量守恒分量式：
(m1 m2 )vx m1v1x m2v2 x vx 5m / s