大学物理第2章动量和角动量(2)
- 格式:ppt
- 大小:996.50 KB
- 文档页数:40


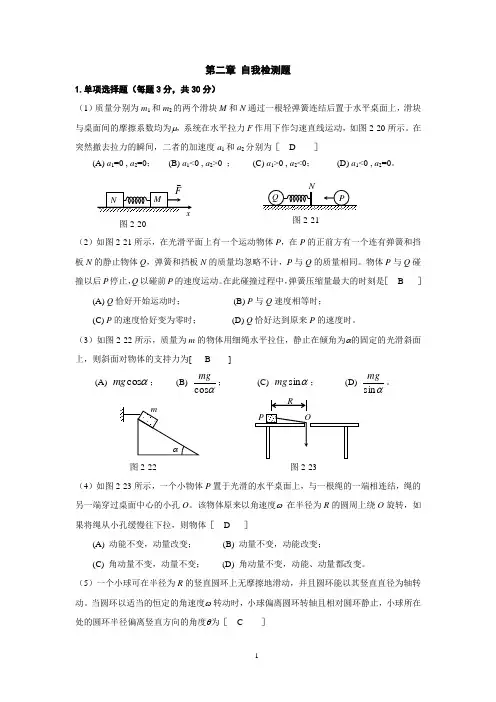
第二章 自我检测题1.单项选择题(每题3分,共30分)(1)质量分别为m 1和m 2的两个滑块M 和N 通过一根轻弹簧连结后置于水平桌面上,滑块与桌面间的摩擦系数均为μ,系统在水平拉力F 作用下作匀速直线运动,如图2-20所示。
在突然撤去拉力的瞬间,二者的加速度a 1和a 2分别为[ D ](A) a 1=0 , a 2=0; (B) a 1<0 , a 2>0 ; (C) a 1>0 , a 2<0; (D) a 1<0 , a 2=0。
(2)如图2-21所示,在光滑平面上有一个运动物体P ,在P 的正前方有一个连有弹簧和挡板N 的静止物体Q ,弹簧和挡板N 的质量均忽略不计,P 与Q 的质量相同。
物体P 与Q 碰撞以后P 停止,Q 以碰前P 的速度运动。
在此碰撞过程中,弹簧压缩量最大的时刻是[ B ] (A) Q 恰好开始运动时; (B) P 与Q 速度相等时; (C) P 的速度恰好变为零时; (D) Q 恰好达到原来P 的速度时。
(3)如图2-22所示,质量为m 的物体用细绳水平拉住,静止在倾角为α的固定的光滑斜面上,则斜面对物体的支持力为[ B ](A) αcos mg ; (B) αcos mg ; (C) αsin mg ; (D) αsin mg。
(4)如图2-23所示,一个小物体P 置于光滑的水平桌面上,与一根绳的一端相连结,绳的另一端穿过桌面中心的小孔O 。
该物体原来以角速度ω 在半径为R 的圆周上绕O 旋转,如果将绳从小孔缓慢往下拉,则物体[ D ](A) 动能不变,动量改变; (B) 动量不变,动能改变; (C) 角动量不变,动量不变; (D) 角动量不变,动能、动量都改变。
(5)一个小球可在半径为R 的竖直圆环上无摩擦地滑动,并且圆环能以其竖直直径为轴转动。
当圆环以适当的恒定的角速度ω 转动时,小球偏离圆环转轴且相对圆环静止,小球所在处的圆环半径偏离竖直方向的角度θ为[ C ]图2-20图2-21图2-22图2-23(A) 2π=θ; (B) g R 2tan arc ωθ=;(C) 2arccosωθR g=; (D) 需由小珠的质量m 决定。


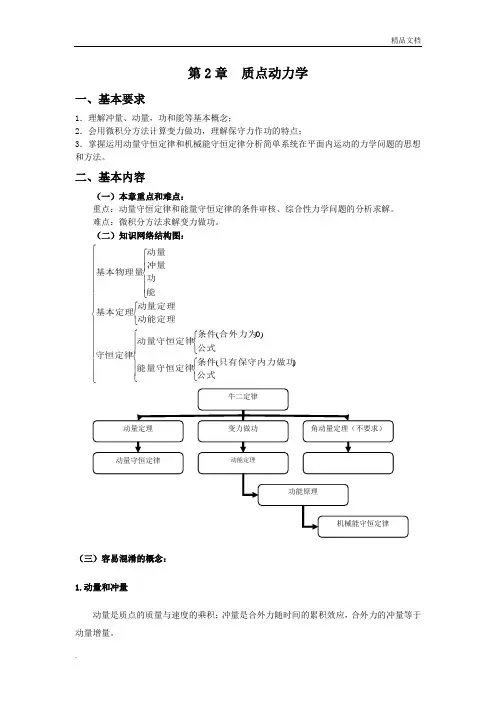
第2章 质点动力学一、基本要求1.理解冲量、动量,功和能等基本概念;2.会用微积分方法计算变力做功,理解保守力作功的特点;3.掌握运用动量守恒定律和机械能守恒定律分析简单系统在平面内运动的力学问题的思想和方法。
二、基本内容(一)本章重点和难点:重点:动量守恒定律和能量守恒定律的条件审核、综合性力学问题的分析求解。
难点:微积分方法求解变力做功。
(二)知识网络结构图:⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧公式只有保守内力做功条件能量守恒定律公式合外力为条件动量守恒定律守恒定律动能定理动量定理基本定理能功冲量动量基本物理量)()0((三)容易混淆的概念: 1.动量和冲量动量是质点的质量与速度的乘积;冲量是合外力随时间的累积效应,合外力的冲量等于动量增量。
2.保守力和非保守力保守力是做功只与始末位置有关而与具体路径无关的力,沿闭合路径运动一周保守力做功为0;非保守力是做功与具体路径有关的力。
(四)主要内容: 1.动量、冲量动量:p mv =u r r冲量:⎰⋅=21t t dt F I ϖϖ2.动量定理:质点动量定理:⎰∆=-=⋅=2112t t v m P P dt F I ϖϖϖϖϖ 质点系动量定理:dtPd F ϖϖ=3.动量守恒定律:当系统所受合外力为零时,即0=ex F ϖ时,或in ex F F u r u r ? 系统的总动量保持不变,即:∑===n i i i C v m P 1ϖϖ4.变力做功:dr F r d F W BAB A⎰⎰=⋅=θcos ϖϖ(θ为)之间夹角与r d F ϖϖ直角坐标系中:)d d d ( z F y F x F W z y BAx ++=⎰5.动能定理:(1)质点动能定理:k1k221222121E E mv mv W -=-=(质点所受合外力做功等于质点动能增量。
)(2)质点系动能定理:∑∑==-=+ni ni E E W W1kio1ki inex(质点系所受外力做功和内力做功之和等于质点系动能增量。




习题22.1选择题(1) 一质点作匀速率圆周运动时,(A)它的动量不变,对圆心的角动量也不变。
(B)它的动量不变,对圆心的角动量不断改变。
(C)它的动量不断改变,对圆心的角动量不变。
(D)它的动量不断改变,对圆心的角动量也不断改变。
[答案:C](2) 质点系的内力可以改变(A)系统的总质量。
(B)系统的总动量。
(C)系统的总动能。
(D)系统的总角动量。
[答案:C](3) 对功的概念有以下几种说法:①保守力作正功时,系统内相应的势能增加。
②质点运动经一闭合路径,保守力对质点作的功为零。
③作用力与反作用力大小相等、方向相反,所以两者所作功的代数和必为零。
在上述说法中:(A)①、②是正确的。
(B)②、③是正确的。
(C)只有②是正确的。
(D)只有③是正确的。
[答案:C]2.2填空题(1) 某质点在力(SI)的作用下沿x轴作直线运动。
在从x=0移动到x=10m的过程中,力所做功为。
[答案:290J](2) 质量为m的物体在水平面上作直线运动,当速度为v时仅在摩擦力作用下开始作匀减速运动,经过距离s后速度减为零。
则物体加速度的大小为,物体与水平面间的摩擦系数为。
[答案:](3) 在光滑的水平面内有两个物体A和B,已知m A=2m B。
(a)物体A以一定的动能E k与静止的物体B发生完全弹性碰撞,则碰撞后两物体的总动能为;(b)物体A以一定的动能E k与静止的物体B发生完全非弹性碰撞,则碰撞后两物体的总动能为。
[答案:]2.3 在下列情况下,说明质点所受合力的特点:(1)质点作匀速直线运动;(2)质点作匀减速直线运动;(3)质点作匀速圆周运动;(4)质点作匀加速圆周运动。
解:(1)所受合力为零;(2)所受合力为大小、方向均保持不变的力,其方向与运动方向相反;(3)所受合力为大小保持不变、方向不断改变总是指向圆心的力;(4)所受合力为大小和方向均不断变化的力,其切向力的方向与运动方向相同,大小恒定;法向力方向指向圆心。