大学物理3.7(2)角动量及角动量定理

物理学概念知识：动量定理和动量角动量定理动量定理和动量角动量定理是物理学中非常基本的两个概念。

它们的内容涉及到我们对物体运动规律的认识，不仅有助于我们更好地理解物理学知识，还可以应用于现实生活中的一些问题。

下面，我们将分别介绍这两个概念及其应用。

一、动量定理动量定理是描述物体运动过程中动量变化的一个基本定理。

它指出：在总外力作用下，物体的动量就会发生变化，这种变化的大小跟作用力和时间的乘积成正比。

这个定理的表达方式为：Δp=Ft其中，Δp表示物体动量的变化量，F表示物体所受的总外力，t 表示外力作用的时间。

式子的意义是：在总外力作用下，物体动量的变化量等于总外力作用时间的乘积。

重物移动时，如果外力越大，或者作用时间越长，那么物体的动量就会发生更大的变化。

从而可以更快地推动物体运动起来。

同样，如果要让运动中的物体停下来，也可以利用动量定理的知识。

通过对物体施加一个与它的运动方向相反的恒定力，也就是反向加速度，可以让物体的动量逐渐减小，直到物体停下来。

二、动量角动量定理动量角动量定理是物理学中另一个基本的概念。

它是通过描述物体绕某一点旋转的行为，来了解物体运动过程中动量变化的定理。

它指出：在物体绕某一点旋转时，物体的角动量就会发生变化，这种变化的大小跟作用力矩和时间的乘积成正比。

这个定理的表达方式为：ΔL=Mt其中，ΔL表示物体角动量的变化量，M表示作用力矩，t表示外力作用的时间。

式子的意义是：在物体绕某一点旋转时，物体角动量的变化量等于力矩作用时间的乘积。

个陀螺时，如果外力越大，或者作用时间越长，那么陀螺的角动量也会发生更大的变化。

从而可以更快地让陀螺旋转。

同样，如果要让旋转中的陀螺停下来，也可以利用动量角动量定理的知识。

通过对陀螺施加一个与它的旋转方向相反的外力矩，也就是反向加速度矩，可以让陀螺的角动量逐渐减小，直到陀螺停下来。

总之，动量定理和动量角动量定理是物理学中非常重要的两个概念。

它们既可以帮助我们更好地理解物理学知识，也可以用于实际生活中的问题解决。

大一力学角动量的知识点角动量是物体运动中的一个重要物理量，它与物体的质量和速度有关。

在大一力学学习中，我们会接触到一些与角动量相关的知识点，本文将对这些知识点进行讲解。

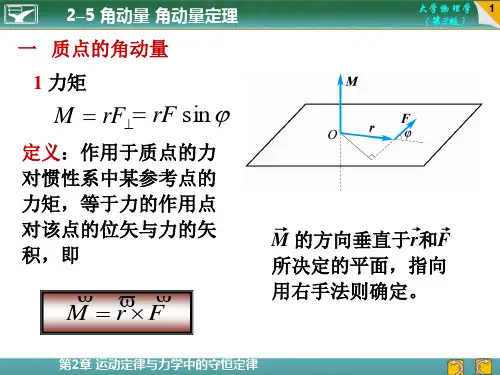
1. 角动量的定义角动量（Angular Momentum）是物体绕某一轴旋转时所具有的物理量。

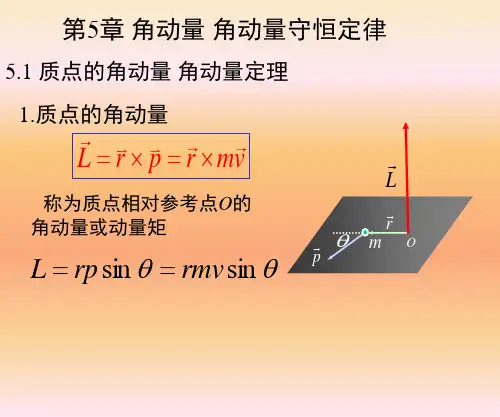
对于质点，其角动量L定义为质点的质量m与质点的径向距离r乘以质点的速度v在垂直于质点运动平面上的投影，即L = mvr。

其中，v是质点的速度，r是质点到轴线的距离。

2. 角动量守恒定律在没有外力作用的情况下，系统的总角动量守恒。

这意味着当一物体的角动量发生变化时，其他物体的角动量也会发生相应的变化，但总的角动量保持不变。

3. 角动量定理角动量定理描述了角动量的变化与作用力之间的关系。

根据角动量定理，物体所受的净外力产生的角动量变化率等于净外力对物体的力矩（Torque）。

即dL/dt = τ，其中τ是作用在物体上的力矩。

4. 角动量守恒的应用角动量守恒定律被广泛应用于物理学的不同领域。

在自然界中，许多现象和实验都可以通过角动量守恒来解释。

例如，当滑轮系统中的绳子拉动产生一个力矩时，滑轮上各质点的角动量随之改变，但总的角动量保持不变。

又如，当一个旋转的冰艇收缩时，由于角动量守恒，冰艇的旋转速度会变大。

5. 角动量与转动惯量转动惯量（Moment of Inertia）是描述物体绕轴旋转惯性的物理量。

对于质点而言，转动惯量I等于质点的质量m乘以质点到轴线的距离的平方，即I = mr^2。

角动量L和转动惯量I之间的关系是L = Iω，其中ω是物体绕轴旋转的角速度。

6. 角动量与角加速度根据牛顿第二定律和角动量定理，可以推导出角动量与角加速度之间的关系。

对于经过一段时间Δt的力矩作用，角动量的变化量ΔL = τΔt。

而角动量的变化量ΔL还可以表示为ΔL = IΔω。

将上述两个等式联立，可以得到IΔω = τΔt。

令Δt趋近于0，可以得到Iα = τ，其中α是角加速度。

角动量定理推导过程
角动量定理是描述物体旋转运动的重要定理之一，在物理学中具有广泛的应用。

下面是角动量定理的推导过程：
首先，我们知道角动量的定义式为：L=r×p，其中r是物体到旋转中心的距离，p是物体的动量，×表示叉乘运算符。

对时间t求导，得到：
dL/dt=d(r×p)/dt
根据叉乘的求导法则，得到：
dL/dt=d(r)/dt×p+r×d(p)/dt
由于旋转中心是不动的，因此d(r)/dt=0，所以上式可以化简为： dL/dt=r×F
其中F是作用在物体上的合力，可以看出，这个式子表达了角动量的变化量与作用力的关系。

根据牛顿第二定律，F=dp/dt，将其代入上式，得到：
dL/dt=r×dp/dt
根据动量定理，dp/dt=F，将其代入上式，得到：
dL/dt=r×F
这个式子就是角动量定理，它表明作用力对物体的角动量造成的变化率等于物体受到的扭矩。

综上所述，角动量定理的推导过程是从角动量的定义式出发，通过叉乘的求导法则推导得到的。

这个定理揭示了作用力对物体旋转运动的影响，对于研究旋转运动的物理规律具有重要的作用。