下载文档原格式
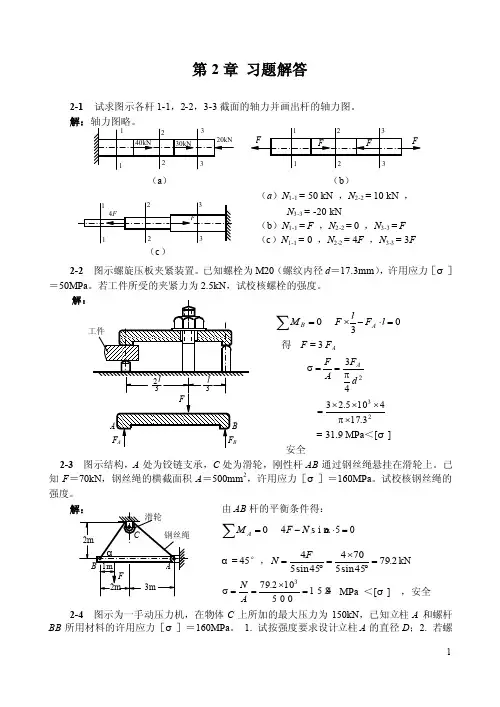
第2章 习题解答2-1 试求图示各杆1-1，2-2，3-3截面的轴力并画出杆的轴力图。
解：（a ）N 1-1 = 50 kN ，N 2-2 = 10 kN ，N 3-3 = -20 kN（b ）N 1-1 = F ，N 2-2 = 0 ，N 3-3 = F（c ）N 1-1 = 0 ，N 2-2 = 4F ，N 3-3 = 3F2-2 图示螺旋压板夹紧装置。
已知螺栓为M20（螺纹内径d ＝17.3mm ），许用应力［ζ］＝50MPa 。
若工件所受的夹紧力为2.5kN ，试校核螺栓的强度。
∑=0BM03=⋅-⨯l F lF A得F = 3 F A243dF A F Aπ==σ233.174105.23⨯π⨯⨯⨯== 31.9 MPa ＜[ζ]安全2-3 图示结构，A 处为铰链支承，C 处为滑轮，刚性杆AB 通过钢丝绳悬挂在滑轮上。
已知F ＝70kN ，钢丝绳的横截面积A ＝500mm 2，许用应力［ζ］＝160MPa 。
试校核钢丝绳的强度。
由AB 杆的平衡条件得：∑=0A M 05s i n 4=⋅α-N F α= 45°，2.7945sin 570445sin 54=︒⨯=︒=F N kN4.158500102.793=⨯==σA N MPa ＜[ζ] ，安全 2-4 图示为一手动压力机，在物体C 上所加的最大压力为150kN ，已知立柱A 和螺杆BB 所用材料的许用应力［ζ］＝160MPa 。
1. 试按强度要求设计立柱A 的直径D ；2. 若螺（a ）（b ）杆BB 的内径d ＝40mm ，试校核其强度。
解：由平衡条件得 752150==A N kN 1. 由立柱的强度条件 24DN A N AA A π==σ≤[ζ] 得 D ≥4.2416010754][43=⨯π⨯⨯=πζA N mm2. 螺杆的应力1194010150423=⨯π⨯⨯==σBB BB A N MPa ＜[ζ] 螺杆强度足够。
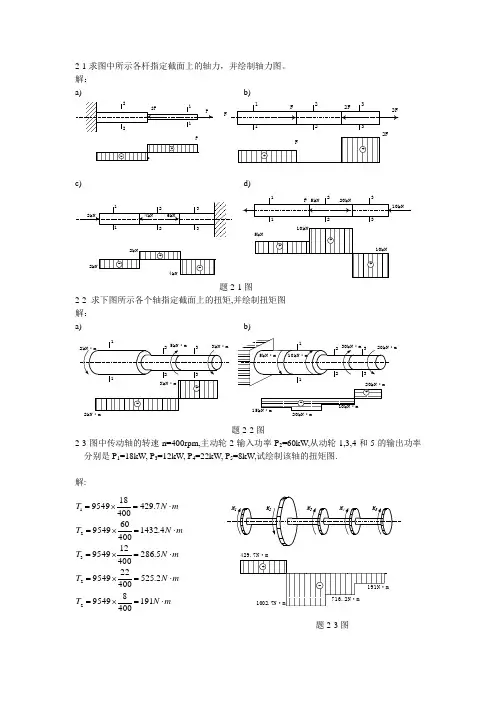
2-1求图中所示各杆指定截面上的轴力，并绘制轴力图。
解：a) b)FFc) d)题2-1图2-2 求下图所示各个轴指定截面上的扭矩,并绘制扭矩图 解：a) b)2kN·m20kN·m题2-2图2-3图中传动轴的转速n=400rpm,主动轮2输入功率P 2=60kW,从动轮1,3,4和5的输出功率分别是P 1=18kW, P 3=12kW, P 4=22kW, P 5=8kW,试绘制该轴的扭矩图. 解:mN T mN T mN T mN T m N T ⋅=⨯=⋅=⨯=⋅=⨯=⋅=⨯=⋅=⨯=191400895492.5254002295495.2864001295494.14324006095497.42940018954922321 题2-3图429.7N·m2-4 求图中所示各梁指定截面上的剪力和弯矩,设q 和F 均为已知.a )b)A qlql 2/2Bc)d)qlF QAM图F Q 图题2-4图2-5试绘制下图所示各梁的剪力图和弯矩图,并求出剪力和弯矩的最大值.设F q l 均为已知.a)b)A F Q2M图F Q 图c)d)F QF Q 图M图e) f)F QM图qlql 2/2ql 2/8F Q M图g)h)F Q M图9ql 2/128F Q M图题2-5图2-6不列方程,绘制下面各梁的剪力图和弯矩图,并求出剪力和弯矩绝对值的最大值.设F 、q 、l 均为已知。
a)b)F Q M图ql 2/2qlF Qc) d)F Q 图M图2FlF Q 图M图e) f)F Q 图M图F Q M图题2-6图2-7绘制下图所示各梁的剪力图和弯矩图,求出|F Q |max 和|M|max ,并且用微分关系对图形进行校核.a) b)F Q 图M图F Q 图M图Flc)d)F Q 图M图2F Q题2-7图2-8试判断图中所示各题的F Q ，M 图是否有错，如有错误清指出错误原因并加以改正。
一、单项选择题（每小题2分，共20分）题目11．两根材料不同、截面面积不同的杆件，在相同轴向外力作用下，轴力是（）。
选择一项：A. 不相等B. 可能相等C. 可能不相等D. 相等题目22．胡克定律应用的条件是（）。
选择一项：A. 只适用于塑性材料B. 只适用于轴向拉伸C. 应力不超过屈服极限D. 应力不超过比例极限题目33．工程上习惯将EA称为杆件截面的（）。
选择一项：A. 抗拉刚度B. 抗弯刚度C. 抗剪刚度D. 抗扭刚度题目44．低碳钢的拉伸过程中，（）阶段的特点是应力几乎不变。
选择一项：A. 颈缩B. 弹性C. 强化D. 屈服题目55．低碳钢的拉伸过程中，（）阶段的特点是应力与应变成正比。
选择一项：A. 屈服B. 颈缩C. 弹性D. 强化题目66．低碳钢的拉伸过程中，胡克定律在（）范围内成立。
选择一项：A. 弹性阶段B. 强化阶段C. 屈服阶段D. 颈缩阶段题目77．低碳钢材料在拉伸试验过程中，所能承受的最大应力是（）。
选择一项：A. 强度极限σbB. 屈服极限σsC. 比例极限σpD. 许用应力[σ]题目88．直径为D的圆形截面，则其对形心轴的惯性矩为（）。
选择一项：C题目99．构件抵抗变形的能力称为（）。
选择一项：A. 极限强度B. 强度C. 刚度D. 稳定性题目1010．构件抵抗破坏的能力称为（）。
选择一项：A. 稳定性B. 强度C. 刚度D. 极限强度二、判断题（每小题2分，共20分）题目111．杆件变形的基本形式有轴向拉伸与压缩、剪切、扭转和弯曲四种。
选择一项：对错题目122．轴向拉伸（压缩）时与轴线相重合的内力称为剪力。
选择一项：对错题目133．梁的正应力是由剪力引起的。
选择一项：对错题目144．轴向拉伸（压缩）的正应力大小和轴力的大小成正比。
选择一项：对错题目155．任意平面图形对某轴的惯性矩一定大于零。
选择一项：对错题目166．平面图形对所有平行轴的惯性矩中，其对其形心轴的惯性矩为最大。
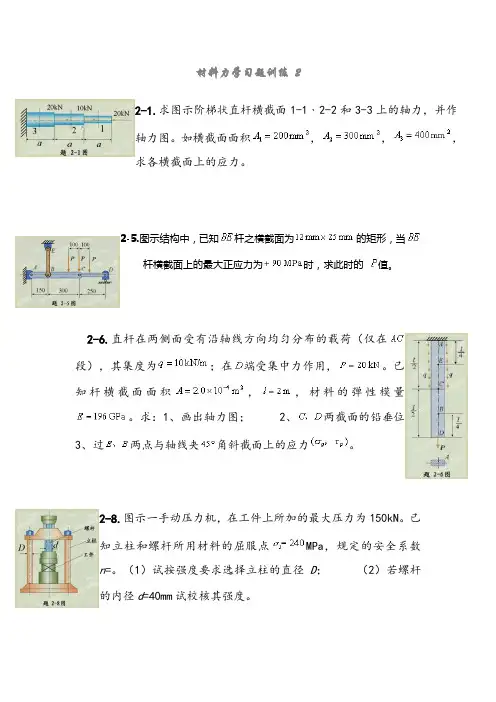
材料力学习题训练22-1.求图示阶梯状直杆横截面1-1﹑2-2和3-3上的轴力，并作轴力图。
如横截面面积，，，求各横截面上的应力。
2-5.图示结构中，已知杆之横截面为的矩形，当杆横截面上的最大正应力为时，求此时的值。
2-6.直杆在两侧面受有沿轴线方向均匀分布的载荷（仅在段），其集度为；在端受集中力作用，。
已知杆横截面面积，，材料的弹性模量。
求：1、画出轴力图； 2、两截面的铅垂位3、过两点与轴线夹角斜截面上的应力。
2-8.图示一手动压力机，在工件上所加的最大压力为150kN。
已知立柱和螺杆所用材料的屈服点MPa，规定的安全系数n=。
（1）试按强度要求选择立柱的直径D；（2）若螺杆的内径d=40mm试校核其强度。
3-1 夹剪如图所示。
销子C的直径d=5mm。
当加力P=，剪直径与销子直径相同的铜丝时，求铜丝与销子横截面的平均剪应力。
已知a=30mm，b=150mm。
3-2 结构受力如图所示，若已知木材的许用切应力，试校核木接头剪切强度是否安全。
3-3 木梁由柱支撑如图所示，今测得柱中的轴向压力为，若已知木梁所能承受的许用挤压应力。
确定柱与木梁之间垫板的尺寸。
3-4 木构件和由两片层合板用胶粘接在一起，承受轴向载荷作用，如图所示。
已知和的空隙为；板宽；胶层的许用切应力。
确定层合板的长度。
3-5 水轮发电机组的卡环尺寸如图所示。
已知轴向荷载P=1450kN，卡环材料的许用剪应力=80MPa，许用挤压应力=150MPa。
试对卡环进行强度校核。
3-6 拉力P=80kN的螺栓连接如图所示。
已知b=80mm，t=10mm，d=22mm，螺栓的许用剪应力=130MPa，钢板的许用挤压应力=300MPa，许用拉应力 =170MPa。
试校核该接头的强度。
3-7 一托架如图所示。
已知外力P=35kN，铆钉的直径d=20mm，铆钉都受单剪。
求最危险的铆钉横截面上剪应力的数值及方向。
3-8 销钉式安全离合器如图所示，允许传递的外力偶矩m=30kN·cm，销钉材料的剪切强度极限=360MPa，轴的直径D=30mm，为保证m>30000N·cm时销钉被剪断，求销钉的直径d。
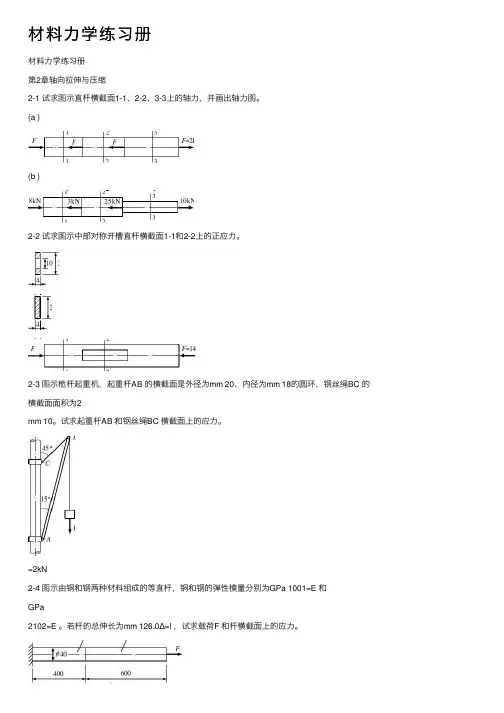
材料⼒学练习册材料⼒学练习册第2章轴向拉伸与压缩2-1 试求图⽰直杆横截⾯1-1、2-2、3-3上的轴⼒，并画出轴⼒图。
(a )(b )2-2 试求图⽰中部对称开槽直杆横截⾯1-1和2-2上的正应⼒。
2-3 图⽰桅杆起重机，起重杆AB 的横截⾯是外径为mm 20、内径为mm 18的圆环，钢丝绳BC 的横截⾯⾯积为2mm 10。
试求起重杆AB 和钢丝绳BC 横截⾯上的应⼒。
=2kN2-4 图⽰由铜和钢两种材料组成的等直杆，铜和钢的弹性模量分别为GPa 1001=E 和GPa2102=E 。
若杆的总伸长为mm 126.0Δ=l ，试求载荷F 和杆横截⾯上的应⼒。
2-5 图⽰阶梯形钢杆，材料的弹性模量GPa 200=E ，试求杆横截⾯上的最⼤正应⼒和杆的总伸长。
2-6 图⽰电⼦秤的传感器为⼀空⼼圆筒形结构，圆筒材料的弹性模量GPa 200=E 。
在秤某⼀沿圆筒轴向作⽤的重物时，测得筒壁产⽣的轴向线应变6108.49-?-=ε。
试求此重物的重量P 。
第3章材料的⼒学性质拉压杆的强度计算3-1 图⽰⽔压机，若两根⽴柱材料的许⽤应⼒为MPa 80][=σ，试校核⽴柱的强度。
3-2 图⽰油缸盖与缸体采⽤6个螺栓连接。
已知油缸内径mm350=D ，油压MPa 1=p 。
若螺栓材料的许⽤应⼒MPa 40][=σ，试求螺栓的内径。
3-3 图⽰铰接结构由杆AB 和AC 组成，杆AC 的长度为杆AB 长度的两倍，横截⾯⾯积均为2mm 200=A 。
两杆的材料相同，许⽤应⼒MPa 160][=σ][F3-4 承受轴⼒kN 160N =F 作⽤的等截⾯直杆，若任⼀截⾯上的切应⼒不超过MPa 80，试求此杆的最⼩横截⾯⾯积。
3-5 试求图⽰等直杆AB 各段内的轴⼒。
a3-6 图⽰结构的横梁AB 可视为刚体，杆1、2和3的横截⾯⾯积均为A ，各杆的材料相同，许⽤应⼒为][σ。
试求许⽤载荷][F 。
3-7 图⽰铰接正⽅形结构，各杆的材料均为铸铁，其许⽤压应⼒与许⽤拉应⼒的⽐值为3][][t c =σσ，各杆的横截⾯⾯积均为A 。
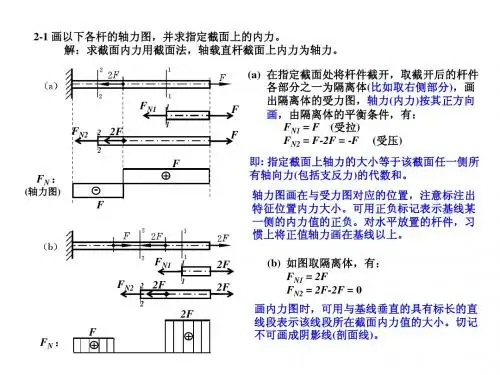
第二章轴向拉(压)变形[习题2-1] 试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。
（a ）解：（1）求指定截面上的轴力 FN =-11FF F N -=+-=-222（2）作轴力图轴力图如图所示。
（b ）解：（1）求指定截面上的轴力 FN 211=-2222=+-=-F F N （2）作轴力图FF F F N =+-=-2233 轴力图如图所示。
（c ）解：（1）求指定截面上的轴力 FN 211=-FF F N =+-=-222（2）作轴力图FF F F N 32233=+-=- 轴力图如图所示。
（d ）解：（1）求指定截面上的轴力 FN =-11F F a aFF F qa F N 22222-=+⋅--=+--=-（2）作轴力图 中间段的轴力方程为： x aFF x N ⋅-=)(]0,(a x ∈轴力图如图所示。
[习题2-2] 试求图示等直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积，试求各横截面上的应力。
2400mm A =解：（1）求指定截面上的轴力kNN 2011-=- )(10201022kN N -=-=-)(1020102033kN N =-+=-（2）作轴力图轴力图如图所示。
（3）计算各截面上的应力MPa mm N A N 504001*********-=⨯-==--σMPa mm N A N 254001010232222-=⨯-==--σMPamm N A N 254001010233333=⨯==--σ[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力，并作轴力图。
若横截面面积，，，并求各横截面上的应力。
21200mm A =22300mm A =23400mm A =解：（1）求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-（2）作轴力图轴力图如图所示。
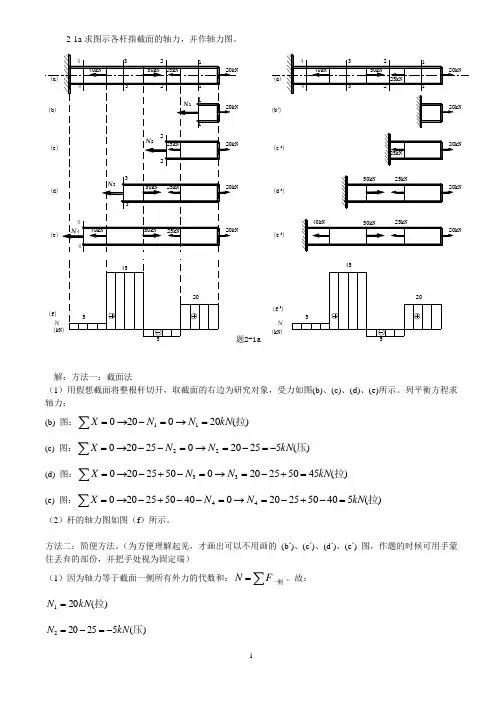
2-1a 求图示各杆指截面的轴力，并作轴力图。
(c ')(e ')(d ')N (kN)205455(f ')解：方法一：截面法（1）用假想截面将整根杆切开，取截面的右边为研究对象，受力如图(b)、(c)、(d)、(e)所示。
列平衡方程求轴力： (b) 图：)(20020011拉kN N NX =→=-→=∑(c) 图：)(5252002520022压kN N NX -=-=→=--→=∑(d) 图：)(455025200502520033拉kN N NX =+-=→=-+-→=∑(e) 图：)(540502520040502520044拉kN N NX =-+-=→=--+-→=∑（2）杆的轴力图如图（f ）所示。
方法二：简便方法。
（为方便理解起见，才画出可以不用画的 (b ‘)、(c ‘)、(d ‘)、(e ‘) 图，作题的时候可用手蒙住丢弃的部份，并把手处视为固定端）（1）因为轴力等于截面一侧所有外力的代数和：∑=一侧FN 。
故：)(201拉kN N =)(525202压kN N -=-=)(455025203拉kN N =+-=)(5405025204拉kN N =-+-=（2）杆的轴力图如图（f ‘）所示。
2-2b 作图示杆的轴力图。
(c)图：(b)图：（3）杆的轴力图如图（d ）所示。
2-5 图示两根截面为100mm ⅹ100mm 的木柱，分别受到由横梁传来的外力作用。
试计算两柱上、中、下三段的应力。
(b)(c)(d)(f)题2-5-N图（kN）6108.5N图（kN）326.5-解：（1）梁与柱之间通过中间铰，可视中间铰为理想的光滑约束。
将各梁视为简支梁或外伸梁，柱可视为悬臂梁，受力如图所示。
列各梁、柱的平衡方程，可求中间铰对各梁、柱的约束反力，计算结果见上图。
（2）作柱的轴力图，如(e)、(f)所示。
（3）求柱各段的应力。
解：（1）用1-1截面将整个杆切开，取左边部分为研究对象；再用x -x 截面整个杆切开，取右边部分为研究对象，两脱离体受力如图(b)、(c)，建立图示坐标。
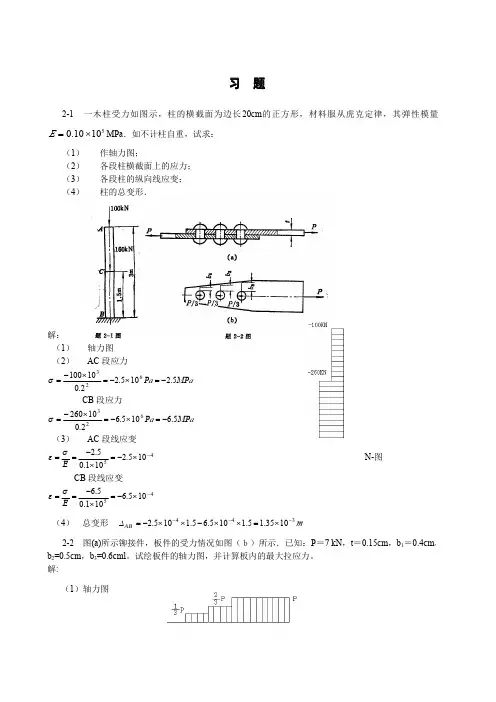
习题2-1一木柱受力如图示，柱的横截面为边长20cm 的正方形，材料服从虎克定律，其弹性模量MPa ．如不计柱自重，试求：51010.0×=E （1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形．解：（1）轴力图（2）AC 段应力a a ΜΡΡσ5.2105.22.010100623−=×−=×−=CB 段应力aa ΜΡΡσ5.6105.62.010260623−=×−=×−=（3）AC 段线应变45105.2101.05.2−×−=×−==ΕσεN-图CB 段线应变45105.6101.05.6−×−=×−==Εσε（4）总变形m 3441035.15.1105.65.1105.2−−−×=××−××−=ΑΒ∆2-2图(a)所示铆接件，板件的受力情况如图（ｂ）所示．已知：P ＝7kN ，t ＝0.15cm ，b 1＝0.4cm ，b 2=0.5cm ，b 3=0.6cml 。
试绘板件的轴力图，并计算板内的最大拉应力。
解:（2）aΜΡσ4.194101024.015.0767311=×××××=−a ΜΡσ1.311101025.015.0767322=×××××=−a ΜΡσ9.388101026.015.07673=××××=−最大拉应力aΜΡσσ9.3883max ==2-3直径为１cm 的圆杆，在拉力P ＝10kN 的作用下，试求杆内最大剪应力，以及与横截面夹角为＝30o 的斜截面上的正应力与剪应力。
α解:（1）最大剪应力a d ΜΡππΡστ66.6310101102212672241max =××××===−（2）界面上的应力°=30α()a ΜΡασσα49.952366.632cos 12=×=+=a ΜΡαστα13.5530sin 66.632sin 2=×=×=°2-4图示结构中ABC 与CD 均为刚性梁，C 与D 均为铰接，铅垂力P ＝20kN 作用在C 铰，若（1）杆的直径d 1=1cm ，（2）杆的直径d 2=2cm ，两杆的材料相同，E ＝200Gpa ，其他尺寸如图示，试求（1）两杆的应力；（2）C 点的位移。
