轴力图的画法

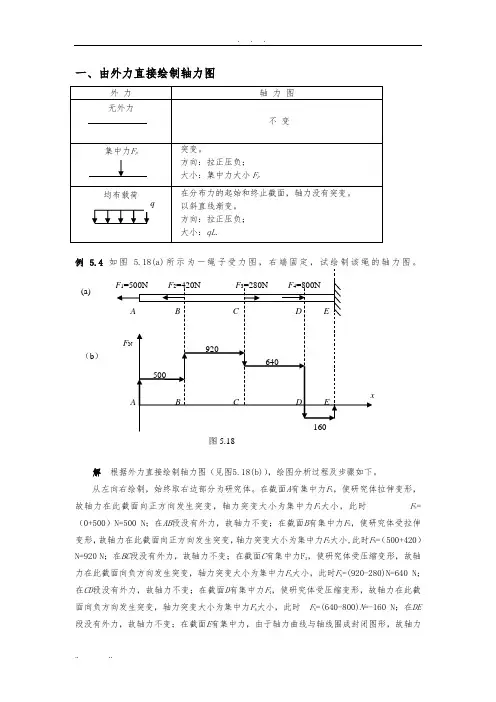
一、由外力直接绘制轴力图例 5.4 力图。

解 根据外力直接绘制轴力图（见图5.18(b)），绘图分析过程及步骤如下。

从左向右绘制，始终取右边部分为研究体。

在截面A 有集中力F 1，使研究体拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F 1大小，此时 F N =（0+500）N=500 N ；在AB 段没有外力，故轴力不变；在截面B 有集中力F 2，使研究体受拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F 2大小,此时F N =（500+420）N=920 N ；在BC 段没有外力，故轴力不变；在截面C 有集中力F 3，使研究体受压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F 3大小，此时F N =(920-280)N=640 N ；在CD 段没有外力，故轴力不变；在截面D 有集中力F 4，使研究体受压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F 4大小，此时 F N =(640-800)N =-160 N ；在DE 段没有外力，故轴力不变；在截面E 有集中力，由于轴力曲线与轴线围成封闭图形，故轴力（b ）(a)突变为0。

例5.5有一根阶梯轴受力如图5.19(a)所示，试绘制阶梯轴的轴力图。

图5.19解从右向左绘制，始终取左变部分为研究体。

根据外力直接绘制轴力图（见图5.19(b)），绘图分析过程及步骤如下：在截面A有集中力F1，使研究体压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F1大小,此时F N=（0-10）kN=-10 kN；在AB段有均匀分布载荷，使研究体受拉伸变形，故轴力以斜直线规律向正方向渐变，轴力渐变大小为均匀分布载荷大小，此时F N=（-10+10×2）kN=10 kN；在截面B没有力，故此截面轴力没有变化；在BC段没有外力，故轴力不变；在截面C有集中力F2，使研究体受拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F2大小，此时F N=（10+10）kN=20 kN；在CD段没有外力，故轴力不变；在截面D有集中力，由于轴力曲线与轴线围成封闭图形，故轴力突变为0.二、由外力直接绘制扭矩图外力扭矩图无外力不变集中力F P突变。

其 中， 跳 跃 矢 量 的具 体 画 法 为 ： 跳跃 矢 量 的起 点 ， 为 上段 保 持 矢 量 的终 点 。跳 跃 矢 量 方 向 ， 需要 根 据 外 力 方 向与 位 置 坐标 轴 正 方 向是 否 一 致判 断 ， 当外 力 方 向与位 置 坐 标 轴 正方 向一 致 时 ， 跳 跃 矢量 指 向轴 力 减
中 图分 类 号 ： Ｇ ７ １ ２ 文 献 标识 码 ：Ａ 文章编号 ： １ ６ ７ １ — ５ ９ ９ ３ （ ２ ０ １ ５ ） ０ １ — ０ ０ ４ １ — ０ ２
引 言
（ 一） 计算 量 大 。 需 根据 外 力 作 用 点个 数 ， 将 构件 分段， 逐 段 列 平 衡方 程 ， 才 能 求解 出每 段 内力 。 外 力数 量越多， 平 衡 方 程数 量 也 越 多 ， 计 算 量 就越 大 ， 计 算 效
若将上述例子的a截面的所受外力变成未知且该杆件仍受力平衡即得如图4所示的悬臂梁受力悬臂梁受力图在解决这类杆件轴力图绘制时若采用矢量画法则不必像截面法那样先根据力的平衡方程计算截面处的外力然后再按一般过程进行计算并绘图而可以直接利用矢量的相应性质从杆件已知外力端向未知外力端依次绘制矢量而省去计算未截面处的外力绘制出相应的轴力图
一
（ 二） 判 断 内力 的 实 际正 负 号 较 为 麻 烦 。判 断每 段 截 面 内力 的正 负 号方 法 ， 一 般 为 先 假 设 该段 内力 为 正 ，再 由所 列 的平 衡 方 程 求 解 出的 内力 的 正 负号 ， 判 断 出 内力 的实 际 正 负号 。 同样 ， 当 外 力数 量 越 多 时 ， 内 力 的方 向需 要 判 断 的次 数 也就 越 多 。
拉压杆 件轴 力 图的矢量 画法

2.10剪切和挤压的实用计算
画轴力图
♦画轴力图
轴力图
轴力随横截面位置而变化的图。
♦画轴力图
二、算例
—等直杆其受力情况如下图所示，请作杆的轴力 图。
1
40kN
55^N 25^N
A 600 B
C 500
• 300.
20蚪
D 400E
♦画轴力图
FR \A 600 B
40kN -300 -
55^N 25^N
20蚪
C 500. D 400 ・E
解： (1)求支座反力
-FR -40 +55 -25 +20 = 0
FR = 10kN
♦画轴力图
⑵求48段内的轴力
FR
_ .0kN
55伊 25"
20kN
|A 60 0 B
■ 300 ・
E C 500. D 400 -
、 FN
F = FN1
— F FN1
R
=R
0=
+10(kN)
(+)
♦画轴力图
(3)求3C段内的轴
力
璃 _F - 40 = 0 = FN2 FR + 40 = +50(kN) (+)
♦画轴力图
(4)求CQ段内的轴力
—凡3 - 25 + 20 = 0 FN3 = _5(kN)(―)
♦画轴力图 (5)求QE段内的轴力
FR
』0kN
、 55kN 25kN
► —.
20kN
\A 600 B . 300.
妇 C 500
E
o
々4
20kN
F 4 = +20(kN)(+)

材料力学大连理工大学王博轴力与轴力图F 1 F 2 F 3 一、轴力F N (Axial force)—— 拉压杆的内力 截面法步骤——截断、取半、画内力、平衡mm轴力与轴力图0x F =∑N 120F F F -+=, N 12F F F =-F N F 1 F 2 mm取左半和取右半计算内力，结果是一样的因此，可选择简单的一侧计算轴力，另一侧作为校核 小讨论N 3F F =12F F =-F 1 F 2 F 3m m F NF 1 F 2 m mF N F 3 mm取左半 取右半知识点：轴力 Axial force定义——内力主矢的法向分量求法——截面法 Method of section步骤：截开，取半，画内力，平衡大小= 截面任一侧所有外力的代数和正负号——拉伸为正（离开截面）单位—— N , kNQ：1 理论力学里怎么定义的力的正负?2 轴力为什么依据变形来定义正负呢? （好处？）问题：如何描述不同截面的轴力既简单又直观？ 方法： 1. 临用时逐个截面计算2. 写方程式3. 画几何图线—— 轴力图： 横坐标——杆的轴线纵坐标——轴力数值二、轴力图 Axial force diagram F 1 F 2 F 3 F 3 1 12 2 33解：1.各段轴力计算： 例题1 作图示杆的轴力图 10kN20kN 20kN 10kN A D B C 11 2 2 3 3 F N（kN ） 10 1010N110kN ,F =N210kN ,F =-N320kNF =- 2.作轴力图1. 与杆平行对齐画2. 标明内力的性质（F N ）3. 标明内力单位4. 正确画出内力沿轴线的变化规律5. 标明内力的正负号6. 注明特殊截面的内力数值（极值）轴力图要求 10kN20kN 20kN 10kN AD BC F N（kN ） 10 1010例题2 A CBF l 1 l 2 12 12.42 F N (kN) x 1 F F N1 F F N2 l 1 x 2－l 1 1 1 x 1 22 x 212.98 已知：A 1=3 ㎝2 , A 2=4 ㎝2 , l 1= l 2= 50m , F =12 kN , γ = 0.028 N/㎝3 求：作轴力（考虑自重） 解：(1) 计算轴力 AB 段: F N1 = F ＋γA 1x 1 (0≤x 1≤l 1) BC 段： F N2 =F ＋ γ A 1l 1＋γ A 2 (x 2－l 1) (l 1≤x 2≤l 1＋l 2)(2) 绘轴力图。

P P
5
一、概念 轴向拉压的外力特点：外力的合力作用线与杆的轴线重合。 轴向拉压的变形特点：杆的变形主要是轴向伸缩，伴随横向 缩扩。 轴向拉伸：杆的变形是轴向伸长，横向缩短。 轴向压缩：杆的变形是轴向缩短，横向变粗。
6
二、 工 程 实 例
7
8
内力
指由外力作用所引起的、物体内相邻部分之间分布内 力系的合成（附加内力）。
计算杆在截开面上的未知内力（此时截开面上的内力 对所留部分而言是外力）。
10
1. 轴力的概念: (在轴向载荷作用下，杆件横截面上的唯一 内力分量--就是轴力)
m
P
P
m
P
m FN
FN = P
m
P
m
P
m
P
m FN
FN = P
m
11
2. 轴力的正负规定: FN 与外法线同向,为正轴力(拉力) FN
FN与外法线反向,为负轴力(压力)
24
补充例题：
例题2-2：试作此杆的轴力图。
q
F
F
l
解： FR
F
l
2l
l
1
F2 q
3
1
F 2
3
F F'=2ql FR
F
FR = F
F F F
25
补充例题： FR = F FR = F FR = F
FR = F
1
F2
q
3
Fx
1
F2
3
FN1 = F
FN3 = F
F
Fq
F N2
F
x1
F F Fx1 l
杆件横截面面上的正应力由题目可见斜截面mm的方位角为40ommm50om于是斜截面上的正应力与切应力分别为应力方向如图示221引言22轴力及轴力图23拉压杆应力与圣维南原理第二章轴向拉伸和压缩24材料在拉伸和压缩时的力学性能25应力集中26失效许用应力与强度条件27胡克定律拉压杆变形28拉压静不定问题29连接部分的强度21引言工程中有很多构件例如屋架中的杆是等直杆作用于杆上的外力的合力的作用线与杆的轴线重合

第二章拉伸压缩与剪切轴向拉压的内力计算2.1画轴力图2.2拉（压）杆横截面上的应力2.3拉（压）杆斜截面上的应力2.4材料拉伸时的力学性能2.5第二章拉伸压缩与剪切材料压缩时的力学性能2.6剪切和挤压的实用计算2.10失效、许用应力和强度计算2.7轴向拉压时杆件的变形2.8应力集中的概念2.9画轴力图画轴力图画轴力图xF NO一、轴力图轴力随横截面位置而变化的图。

一等直杆其受力情况如下图所示，请作杆的轴力图。

CABD 600300500400E40kN55kN 25kN 20kN 画轴力图二、算例FR画轴力图CA B D600300500400E40kN55kN25kN20kN解：(1) 求支座反力R 405525200F--+-+=R 10kNF=F R画轴力图CA B D 600300500400E40kN 55kN 25kN 20kN (2) 求AB 段内的轴力1F RF N1N1R 0F F -=N1R 10(kN)()F F ==++F R画轴力图CA BD 600300500400E40kN55kN 25kN20kN(3) 求BC 段内的轴力N2R 400F F --=2F R40kNF N2N2R 4050(kN)()F F =+=++F R画轴力图CABD 600300500400E40kN55kN 25kN20kN(4) 求CD 段内的轴力N325200F --+=N35(kN)()F =--20kN25kN3F N3F R画轴力图CABD 600300500400E40kN55kN 25kN20kN(5) 求DE 段内的轴力420kNF N4)((kN)N ++=204F发生在BC 段内任一横截面上 画轴力图Nmax 50(kN)F =(6) 画轴力图C AB D 600300500400E 40kN 55kN 25kN 20kN F 5010520++NKN x。

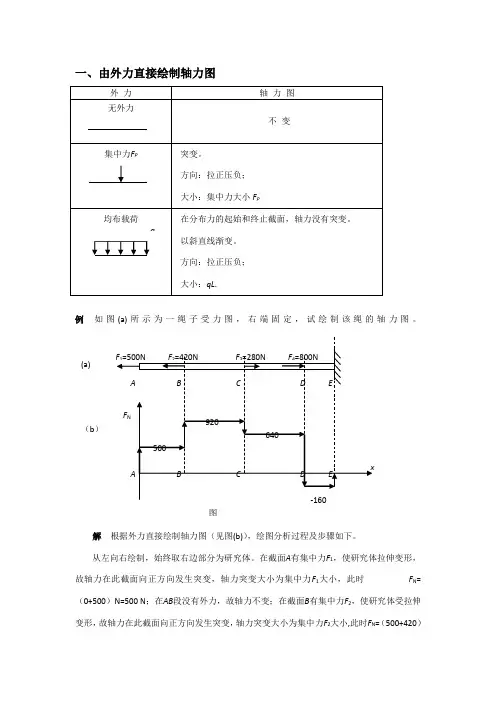
一、由外力直接绘制轴力图例 如图(a)所示为一绳子受力图，右端固定，试绘制该绳的轴力图。

解 根据外力直接绘制轴力图（见图(b)），绘图分析过程及步骤如下。

从左向右绘制，始终取右边部分为研究体。

在截面A 有集中力F 1，使研究体拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F 1大小，此时 F N =（0+500）N=500 N ；在AB 段没有外力，故轴力不变；在截面B 有集中力F 2，使研究体受拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F 2大小,此时F N =（500+420）（b ）(a)N=920 N；在BC段没有外力，故轴力不变；在截面C有集中力F3，使研究体受压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F3大小，此时F N=(920-280)N=640 N；在CD段没有外力，故轴力不变；在截面D有集中力F4，使研究体受压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F4大小，此时F N=(640-800)N=-160 N；在DE 段没有外力，故轴力不变；在截面E有集中力，由于轴力曲线与轴线围成封闭图形，故轴力突变为0。

例有一根阶梯轴受力如图(a)所示，试绘制阶梯轴的轴力图。

图解从右向左绘制，始终取左变部分为研究体。

根据外力直接绘制轴力图（见图(b)），绘图分析过程及步骤如下：在截面A有集中力F1，使研究体压缩变形，故轴力在此截面向负方向发生突变，轴力突变大小为集中力F1大小,此时F N=（0-10）kN=-10 kN；在AB段有均匀分布载荷，使研究体受拉伸变形，故轴力以斜直线规律向正方向渐变，轴力渐变大小为均匀分布载荷大小，此时F N=（-10+10×2）kN=10 kN；在截面B没有力，故此截面轴力没有变化；在BC段没有外力，故轴力不变；在截面C有集中力F2，使研究体受拉伸变形，故轴力在此截面向正方向发生突变，轴力突变大小为集中力F2大小，此时F N=（10+10）kN=20 kN；在CD段没有外力，故轴力不变；在截面D有集中力，由于轴力曲线与轴线围成封闭图形，故轴力突变为0.二、由外力直接绘制扭矩图例如图（a）所示圆轴，左端固定、右端自由，受到三个集中力偶作用，试绘制其内力图。

低碳钢的 20— 27% 60% 为塑性材料
总复习
保证拉（压）杆不
拉（压）杆的强度条件
因强度不足发生破
坏的条件
max [ ]
等直杆
max
FN, max A
[ ]
强度计算的三种类型：
（1）强度校核
max
FN,max A
[ ]
（2）截面选择
A FN,max
[ ]
（3）计算许可荷载
总复习
e —
30
弹性极限31
32
E
E tan 梁横力弯曲时横截面上的应力
梁的挠曲线近似微分方程及其积分
33
3总4 复习
35
低碳钢试件拉伸时的力学性能
0
两个塑性指标:
断后伸长率 l1 l0 100% 断面收缩率 A0 A1 100%
l0
A0
5% 为塑性材料 5% 为脆性材料
l 1 FN l EA
即
E
称为单轴应力状态下的胡克定律。
总复习
轴向拉（压）杆的变形·胡克定律
d1 d
F
F
l l1
ν
或 -ν
n -- 横向变形因数或泊松比
0 n 0.5
总复习
例1:已知：A1=2cm2，A2=4cm2，F1=4kN，F2=10kN，
E=2×105MPa。试求杆的总变形。
C1、C2为常数，由梁的边界条件（包括位移约 束和连续条件）确定。
A
B
A
B
wA=0
wB=0
总复习
wA=0 θA=0
例6：将正确答案填入下列各题的空格中。
（1）梁变形时，横截面的挠度是指截面形心
沿

N1 5P 8P 4P P 2 P
（拉）
同理，求得AB、 BC、CD段内力分
N2
B
PB
C
PC C PC
D
PD
别为：
N3
D
PD D PD
N2= –3P（压） N3= 5P （拉） N4= P （拉）
N4
O
A PA
B PB
C PC
D
PD
5P
2P + + P
– 3P
N
【例3】 设一直杆AB 沿轴向受力如图示。已知 P1=2kN,P2=3kN,P3=1kN, 试作轴力图。
+
8
–
3 N （单位：kN）
左的外力， 轴力N 增量为正；遇 到向右的外力 ，轴力N 增量为负 。
总 结
1、轴向拉压杆轴力计算的简化 N= ∑截面一侧的轴线方向外力 其中，指向截面的外力记为“-”，离开截面的 外力记为“+”
2、画轴力图的一般步骤：
1） 将杆件分段（以外力作用面为分段面） 2 ） 求出每段的轴力 3 ）根据轴力画出轴力图 4 ）标注相关要素
1
30 N （单位：kN）
例2
图示杆的A、B、C、D点分别作用着大小为5P、8P、4P、P
的力，方向如图，试画出杆的轴力图。
O A PA N1 A PA B PB B PB C PC C PC D PD D
x
PD
解： 求OA段内力N1：设置截面如图
X 0
N1 PA PB PC PD 0
二. 轴力图 为了形象地表示轴力沿轴的变化情况，并确定最大轴力 大小及位置，通常采用图线表示轴力的变化情况。 用平行于杆轴线的坐标轴x表示杆件横截面的位置 以垂直于杆轴线的坐标轴N表示相应截面上轴力的大小 正的轴力画在x轴上方，负的轴力画在x轴下方。

内力、截面法、轴力及轴力图
1、内力的概念
固有内力：分子内力.它是由构成物体的材料的物理性 质所决定的.(物体在受到外力之前，内部就存在着内力)
附加内力：在原有内力的基础上，又添加了新的内力
内力与变形有关
内力特点：
1、有限性 2、分布性 3、成对性
2、轴力及其求法——截面法
轴向拉压杆的内力称为轴力.其作用线与杆
FN 2
FN1 0 1
FN2 40kN
例题 2.2
求图示直杆1-1和2-2截面上的轴力
1
2
2F
2F
F
F
1
2
2F
2
F
2
课堂练习：
1F
2F
3
1
2
3
10KN
10KN 1
2
6KN
1
2
3 6KN
3
3、轴力图
轴力与截面位置关系的图线称为轴力图.
9KN 3KN
F
1 3F
2 2F
4KN
2KN
A 1B
2C
F
4KN
2F
2KN
5KN
例题 2.3F F2F Nhomakorabea2F
2F
10KN 100KN
10KN
A=10mm2
100KN
A=100mm2
哪个杆先破坏?
的轴线重合,用符号 ＦＮ 表示
1、切开； 2、代力； 3、平衡。
F
FN
FN F
FN F
精品资料
• 你怎么称呼老师？
• 如果老师最后没有总结一节课的重点的难点，你 是否会认为老师的教学方法需要改进？
• 你所经历的课堂，是讲座式还是讨论式？ • 教师的教鞭

作轴力图与扭矩图的四句口诀法G633.6杆件的强度和刚度计算是工程力学课程重要的研究内容之一，内力分析和计算是进行杆件的强度和刚度计算的前提，通过作内力图可以直观、形象的表示出内力的分布规律，是进行强度计算时判断危险截面位置的重要依据。

因此，作杆件的内力图是工程力学课程学习的重点，也是学习的难点。

作者经过多年的教学实践，对杆件基本变形作内力图的方法进行了总结和归纳，提炼出利用四句口诀法作内力图的简易方法。

下面分别介绍杆件轴向拉压和扭转变形时画轴力图和扭矩图四句口诀法的含义及应用。

一、轴力图的画法1.根据杆件的受力图画轴力图的步骤（1）求出杆件的约束力（根据静力平衡方程求解），若全部外力（含约束力）均为已知，则可直接进行步骤（2）。

（2）在受力图正下方画出轴力图坐标系（横坐标x表示杆件的截面位置，坐标原点O对应杆件的最左端，纵坐标FN表示轴力的大小）。

（3）在轴力图坐标系中利用四句口诀直接画出轴力图。

规定画轴力图时均从杆件最左端开始，即从轴力图坐标原点开始，从左至右将箭头依次首尾相接，画至杆件最右端，最终箭头终止在X轴上，轴力图构成封闭的图形。

2.画轴力图的四句口诀为：“向左外力向上画，向右外力向下画，两力之间水平画，图形封闭准不差”。

其含义如下：（1）向左（右）外力――指受力图中箭头指向左（右）端的外力（包含约束力）。

（2）向上（下）画――最左端的外力则从X轴（轴力FN=0）向上（下）垂直画线段，箭头向上（下），线段长度等于该截面上外力的大小；如是中间的外力则在该截面左侧轴力图（水平线）的基础上向上（下）度量，其突变值等于该截面外力的大小。

（3）两力之间水平画――两个集中外力之间的轴力图画水平线，箭头向右。

（4）图形封闭准不差――轴力图从左端的原点开始，到最右端的水平轴上（轴力FN=0）结束，轴力图构成封闭的图形，说明外力的水平投影的代数和为零，杆件是平衡的。

3.应用已知杆件的受力图如图1所示，试画出杆件的轴力图。

5.3 轴向拉压杆横截面的内力轴力图外力作用线与杆的轴线重合。

受力杆件轴向伸长或缩短。

变形拉杆压杆FFFF拉压杆的内力——轴力PA F N截开：代替：平衡：AP PPA截面法—拉压杆的内力（轴力）轴力FN正负号规定:拉伸为正，背离截面为正；压缩为负，指向截面为负。

轴力图有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）P PF NP+xS F x = 0F N1F N3 = 22 kNF N1 = 12 kN F N2 = 30 kNF N2F N33012F N (kN)＋22解：由截面法, 列平衡方程得两段杆的横截面面积 A 1=3 ㎝2 , A 2=4 ㎝2 ,杆长：l 1= l 2= 50m , 杆端作用力F =12 kN 材料容重：γ = 0.028 N/㎝3A CBFl 1 l 2 22x 2 11 x 1 1212.4212.98F N (kN)BC 段：FN2 =F ＋ γ A 1 l ＋γ A 2（x 2－l 1）（l 1 ≤ x 2 ≤ l 1＋l 2）x 1 FF N1 F F N2l 1x 2－l 1 F Nmax = 12.98kN解： 已知 : AB 段 : F N1 = F ＋γ A 1 x 1 （0 ≤ x 1 ≤ l 1）小结内力截面法拉压杆的内力——轴力FN 作轴力图有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）。

(dx) N(x)dx EA(x)
LL(dx) L
N(x)dx EA(x)
L n N i Li
i 1 E i Ai
39
第39页，此课件共69页哦
3、单向应力状态下的胡克定律
(dx)1N(x)1 即:E
dx EA(x) E
4、泊松比（或横向变形系数）
或:
关于弹性模量E：
①由材料决定，表示材料抵抗变形的能力。
lim p
ΔP dP
ΔA0 ΔA dA
8
第8页，此课件共69页哦
③ 全应力分解为：
a.垂直于截面的应力称为“正应力” (Normal Stress)；
p
ΔlAim 0ΔΔNAddNA
M
b.位于截面内的应力称为“剪应力”(Shearing Stress)。
ΔlAim0ΔΔTAddTA
9
第9页，此课件共69页哦
6、x 点处的横向线应变：
limdx
x0 x
ac
ac
5、杆的横向变形：
a cacac
38
第38页，此课件共69页哦
二、拉压杆的胡克定律
1、等内力拉压杆的弹性定律
L PL A
P
P
2、变内力拉压杆的弹性定律
L PL NL EA EA
NN（(xx)）
x dx
内力在n段中分别为常量时
EA 称为杆的抗拉压刚度。
一、 Saint-Venant原理：
离开载荷作用处一定距离，应力分布与大小不受外载荷作用方式的 影响。
二、 应力集中（Stress Concentration）：
在截面尺寸突变处，应力急剧变大。
33
第33页，此课件共69页哦

第八章 轴向拉伸与压缩
§8-1 引言
§8-2 轴力与轴力图
轴向拉压的外力特点：外力的合力作用线与杆的轴线重合。 轴向拉压的变形特点：杆的变形主要是轴向伸缩，伴随横向
缩扩。 轴向拉伸：杆的变形是轴向伸长，横向变细。 轴向压缩：杆的变形是轴向缩短，横向变粗。
1
杆件的轴向拉伸和压缩是工程中常见的一种变形。如图 a) 所示的悬臂吊车，在载荷F作用下，AC杆受到A、C两端的拉力 作用，如图 b)所示，BC杆受到B、C两端的压力作用，如图 c) 所示。
当 = 90°时，
( )m in 0
当
=
±
45°时，|
|m
ax
0
2
( 45°斜截面上剪应力最大 )
当 = 0, 90°时， | |min 0
20
[例6] 直径为d =1 cm 杆受拉力P =10 kN的作用，试求最大剪 应力，并求与横截面夹角30°的斜截面上的正应力和剪应力。
N1 5P 8P 4P P 0 N1 2P 4
同理，求得AB、 N2 BC、CD段内力分 别为：
N2= –3P
N3= 5P
N4= P
轴力图如右图 N 2P + – 3P
BC
PB
PC
N3
C
PC N4
5P
+
P
D PD D PD D PD
x
5
[例2] 图示杆长为L，受分布力 q = kx 作用，方向如图，试
画出杆的轴力图。 q(x)
解：x坐标向右为正，坐标原点在 自由端。
L
取左侧x段为对象，内力N(x)为：
O x
O x
q
q(x)
N(x)

合。
Ｆ
ａ
４ Ｆ
—
Ｆ
ｂ
Ｃ
ｄ ｅ
２
ｂ
２ Ｆ － ．
Ｃ
４ Ｆ
ｄ ｅ
Ｆ
图 ４悬臂 梁受 力 图
在 解 决这 类 杆 件 轴 力 图绘 制 时 ， 若 采 用 矢 量 画 法， 则 不 必 像截 面 法 那 样 ， 先 根据 力 的平 衡 方 程 ， 计 算 出 ａ截 面 处 的外 力 ， 然后 再按一般过程 ， 进 行 计 算 并
其 中， 跳 跃 矢 量 的具 体 画 法 为 ： 跳跃 矢 量 的起 点 ， 为 上段 保 持 矢 量 的终 点 。跳 跃 矢 量 方 向 ， 需要 根 据 外 力 方 向与 位 置 坐标 轴 正 方 向是 否 一 致判 断 ， 当外 力 方 向与位 置 坐 标 轴 正方 向一 致 时 ， 跳 跃 矢量 指 向轴 力 减
图。
２ Ｆ ２
．
点， 返 回到 零 。 保 持 矢量 的画 法 为 ： 保 持矢 量 方 向沿 着位 置坐 标 轴方向。 保 持 矢 量 的起 点 ， 为本 次 跳 跃矢 量 的终 点 ； 保 持 矢量 的终 点 ， 为下 次 跳 跃 矢量 的起 点 。即 在 未 受 到 外 力作 用 的各 段截 面 ， 直 接 绘制 平 行 于 位 置 坐 标轴 的
３的轴 力 图 。
１ 、 从 截 面 ａ向截 面 ｅ 方 向建 立位 置坐 标 轴 ， 则 跳 跃 矢量 的方 向为 ： 外 力 指 向右 边 ， 跳 跃 矢 量 指 向下 ； 外 力 指 向左 边 ， 跳 跃 矢量 指 向下 。
～
表 １ 跳 跃 点 与 水平 线段 关 系
跳跃矢最与保持 欠最分界点