正弦交流电路中的功率计算实例

如何计算交流电路中的功率在交流电路中，计算功率是非常重要的一项工作。

了解如何计算交流电路中的功率可以帮助我们更好地理解电路的性能，并为我们设计和调试电路提供指导。

本文将介绍交流电路功率的计算方法。

一、交流电路功率的概念在交流电路中，功率可以分为两种类型：有功功率和无功功率。

有功功率是指交流电路中直接转换为有用功的功率。

在正弦交流电路中，有功功率可以用功率平均值来表示，即有功功率等于电压和电流的乘积再取平均值。

无功功率是指交流电路中不能转换为有用功的功率，例如电容器和电感器中的无功功率。

无功功率不会消耗能量，但在电路中会造成一些能量损失。

无功功率与电压和电流之间的相位差有关。

二、计算有功功率的方法1. 有功功率的计算公式为P = UI * cosθ，其中P表示有功功率，U 表示电压，I表示电流，cosθ表示电压和电流的相位差的余弦值。

2. 如果交流电路中的电压和电流是正弦波形，并且它们之间没有相位差，那么有功功率可以简化为P = UI。

3. 如果电压和电流之间有相位差，可以使用示波器或功率分析仪来测量电压和电流的相位差，并计算有功功率。

三、计算无功功率的方法1. 无功功率的计算公式为Q = UI * sinθ，其中Q表示无功功率，U表示电压，I表示电流，sinθ表示电压和电流的相位差的正弦值。

2. 在交流电路中，无功功率通常由电容器和电感器引起。

电容器的无功功率为正值，电感器的无功功率为负值。

3. 如果交流电路中的电压和电流相位差为零，即它们是同相的，那么无功功率为零。

四、计算视在功率的方法视在功率是指交流电路中电压和电流的乘积，表示电路中的总功率。

视在功率可以用前面提到的有功功率和无功功率的平方和的平方根来计算。

S = √(P^2 + Q^2)，其中S表示视在功率，P表示有功功率，Q表示无功功率。

五、功率因数的计算功率因数是指有功功率与视在功率的比值，表示交流电路中有效转换为有用功的比例。

功率因数在0到1之间，越接近1表示电路的效率越高。

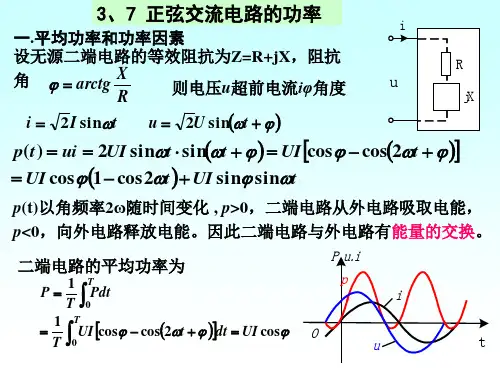
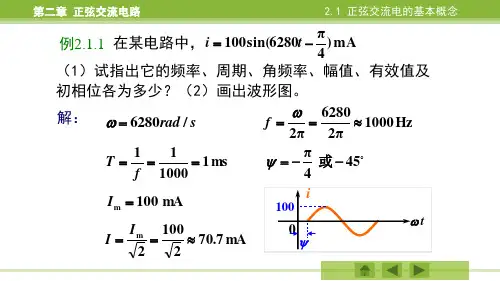
正弦交流电路的功率1)．基本概念在一个二端网络上加正弦交流电压u(t)和电流i(t)若根据功率的计算公式可求瞬时功率：设，则上式可写作可见，瞬时功率是随时间变化的，有时为正，有时可能是负。

瞬时功率为正时表示此时电路消耗功率；为负时表示此时电路向电源输送功率。

为了表征电路实际消耗的平均功率，一般用在一个周期内消耗功率的平均值来表示，称为有功功率，用P表示，即有功功率的单位为瓦（W）。

电路的有功功率为电压和电流有效值的积乘以cosφ。

cosφ称为功率因数，φ称为功率因数角。

一般功率因数用λ表示，即λ=cosφ从瞬时功率表达式中可以看出，第一项表示电路的功率消耗，第二项表示电路与电源能量交换，其交换的最大速率为UIsinΦ,一般称它为无功功率，用Q表示，即Q=UIsinΦ无功功率的单位为乏（var）。

为了便于求解有功功率和无功功率的表示式，引入了复功率的概念。

所谓复功率就是电压的相量与电流相量的共扼复数的乘积，一般用表示，即可见，复功率是一个复数，表示出了有功功率（实部）和无功功率（虚部），一般将复功率的模用S表示，称作视在功率，它等于电压和电流有效值的的积，即视在功率的单位为伏安（VA）。

不难看出，如果是纯电阻电路，它只消耗功率，视在功率与有功功率相等。

如果是由R、L、C组成的电路，电路不仅有消耗功率还有能量交换，则视在功率要大于有功功率。

同时，由视在功率和有功功率可以求出功率因数，即可见功率因数表示了电路实际消耗功率（有功功率）所占视在功率的比例。

功率因数愈大，电路实际消耗功率的比例愈大。

以上概念和公式要孰记。

2)．例题分析已知电压分别加在电阻、电感和电容两端，又知，f=50Hz，R=1KW, L=10mH, C=100mF。

试求:各元件上的功率及其物理意义?解:（1）电阻中电流为电阻吸收有功功率p=100mW, 无功功率Q=0, 功率因数为1。

（2）电感中电流为：电感吸收有功功率p=0, 吸收无功功率Q=31.8var, 功率因数为cos90°=0, 所以不消耗有功功率,只消耗无功功率。

正弦交流电路中的功率计算1.瞬时功率设如图所示的无源二端网络，电流和电压分别为，，则电路的瞬时功率为：2. 有功功率P（平均功率）有功功率，又称为平均功率，是电路一个周期内消耗电能的平均速率。

单位：W或kW从有功功率的表达式可以看出，电路消耗的功率不仅与电压、电流的有效值有关，还与有关。

是电压和电流的相位差，即阻抗角，由电路的参数决定。

对于只含一个电阻的电路，＝0，则对于只含一个电感或电容的电路，＝±90°，则P=0由上分析，说明电路中只有电阻元件消耗有功功率，电感和电容是储能元件，不消耗有功功率。

电路中若有若干个电阻，求有功功率时可采用两种方法：（1）运用公式直接求；（2）可将各个电阻的有功功率求出，相加求得，即。

定义：——功率因数功率因数是交流电路的重要技术数据之一。

功率因数的高低，对于电气设备的利用率和分析、研究电能消耗等问题都有十分重要的意义。

功率因数的大小，取决于电路中负载的性质。

对于电阻性负载，其电压与电流的相位差为0，因此，电路的功率因数最大（）；在纯电感电路中，电压与电流的相位差为π／2，电压超前电流；在纯电容电路中，电压与电流的相位差则为－（π／2），即电流超前电压。

在后两种电路中，功率因数都为0。

对于一般性负载的电路，功率因数就介于0与1之间。

3.无功功率Q从瞬时功率的表达式中可以看出：p1≥0，它反映了电阻所消耗的瞬时功率。

p2是一个正弦量，它的频率是电源频率的两倍，在一个周期中有正有负，而且正负面积相等，它反映了电感、电容这些储能元件与电源进行能量交换的瞬时功率。

无功功率Q定义为p2的幅值。

即无功功率Q反映的是储能元件L、C 与电源进行能量交换的规模。

当电路只含一个电阻元件时，＝0，＝0，Q=0当电路只含一个电感元件时，＝90º，＝1，Q =UI=I2XL=U2/XL当电路只含一个电容元件时，＝－90º，＝－1，Q=－UI=－I2XC=－U2/XC当（感性电路）时，Q>0当（容性电路）时，Q<0当电路中有若干电感、电容元件时，求总的无功功率，方法有二：（1）直接运用公式；（2）可将各部分无功功率相加获得。

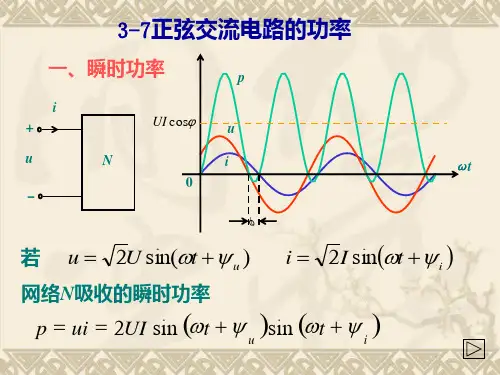
§3-9正弦交流电路的功率计算如果一端口网络的端口电压sin()u u t ωψ=+，流入端口的电流sin()i i I t ωψ=+，且电压与电流参考方向一致，如图3-9-1a 所示。

则由功率定义可得输入该一端口网络的瞬时功率为sin()sin()u i p ui t I t ωψωψ==++cos()cos(2)u i u i UI UI t ψψωψψ=--++ （3-9-1）由式可看出，瞬时功率可分为恒定分量cos()u i UI ψψ-与二倍角频率变化的正弦分量cos(2)u i UI t ωψψ++。

图3-9-1b 为端口电压u 、端口电流i 与瞬时功率p 的波形图。

瞬时功率在某些时间段为正值，表示此时一端口网络正在吸收功率。

在某些时间段为负值，表示网络在输出功率，将原来储存的能量送回电网。

在一周期内电路吸收的平均功率，也称为有功功率。

它的值为01d cos()cos Tu i P p t UI UI T ψψϕ==-=⎰ （3-9-2）式中，U 、I 为负载端电压和电流的有效值；u i ϕψψ=-是端电压与电流在关联参考方向下的相位差；cos ϕ称为功率因数，u i ϕψψ=-称作功率因数角。

由式可看出，决定一个一端口网络负载平均功率的大小，不但与施加的电压，流过的电流的有效值大小有关，而且与电压电流的相位差，即功率因数角ϕ有关。

当电压电流相位差接近2π时，即使U 与I 的乘积很大，但负载所吸收的功率仍然很小，这是因为负载的功率因数cos ϕ很小。

例如对于纯电感（或纯电容）的负载，电压与电流互相正交，2πϕ=，此时功率因数cos 0ϕ=。

对于纯电阻负载，0ϕ=，功率因数cos 1ϕ=。

对于一般无源网络负载，2πϕ≤。

测量一端口网络的功率时，电路连接如图3-9-2b 所示。

将电流线圈串入被测量的电路，电压线圈与端口并联。

二组线圈中分别流过电流，并产生磁场。

功率表的读数等于加在电压线圈上的电压有效值和通过电流线圈的电流有效值的乘积，再乘以电压相量（参考方向从星号指向非星号）和电流相量（参考方图 3-9-1向也从星号指向非星号）之间的相位差的余弦，即cos()cos u i P UI UI ψψϕ=-=。

纯电阻电路中正弦交流电的平均功率在学习电路理论的过程中，我们都会接触到纯电阻电路。

纯电阻电路是由电阻元件组成的电路，其中只有电阻，没有电感和电容。

当纯电阻电路中加入正弦交流电时，我们可以通过计算得到电路中的电流和电压，进而求解平均功率。

本文将围绕纯电阻电路中正弦交流电的平均功率展开阐述。

我们需要明确平均功率的概念。

平均功率是指在一个周期内，电路中各个时刻的瞬时功率的平均值。

对于正弦交流电来说，其瞬时功率可以表示为P(t) = V(t) × I(t)，其中P(t)为瞬时功率，V(t)为电压，I(t)为电流。

接下来，我们来推导纯电阻电路中正弦交流电的平均功率计算公式。

假设电路中的电压为V(t) = Vm × sin(ωt)，电流为I(t) = Im × sin(ωt + φ)，其中Vm为电压的最大值，Im为电流的最大值，ω为角频率，φ为相位差。

根据上述公式，我们可以得到瞬时功率为P(t) = V(t) × I(t) = Vm × Im × sin(ωt) × sin(ωt + φ)。

由三角函数的性质可知，sin(a) × sin(b) = (cos(a - b) - cos(a + b)) / 2。

将上述公式代入瞬时功率的表达式中，可以得到P(t) = (Vm × Im / 2) × (cos(φ) - cos(2ωt + φ))。

根据平均功率的定义，平均功率Pavg可以表示为一个周期内瞬时功率的平均值。

对于一个周期T来说，平均功率可以通过积分得到。

将上述瞬时功率的表达式代入平均功率的积分表达式中，可以得到平均功率的计算公式为Pavg = (Vm × Im / 2) × cos(φ)。

从上述公式可以看出，纯电阻电路中正弦交流电的平均功率与电压的最大值、电流的最大值以及相位差有关。

其中，Vm和Im表示电压和电流的幅值，即最大值，而φ表示电压和电流之间的相位差。

《电工技术》
知识点：正弦交流电路的功率
1. 瞬时功率
=⋅+ωωϕI U p t t sin sin()m m =-+ϕωϕI U t 2
[cos cos(2)m
m （设电感性电路）
=⋅p i u
2 . 平均功率（有功功率）P
u与i 的相
位差角
总电压总电流
1 UI
pdt ϕ
cos
T
P T =
=⎰
上述公式为有功功率的一般表达式，可推广到任何复杂交流电路，其有功功率等于电阻上消耗的功率。

===2
R R
P P U I I R
功率因数
ϕ
cos
=-=-=L C L C Q I X I X I U U IU 22sin ϕ
)(Q ＝Q L +（-Q C ） 3 . 无功功率 Q
单位：V A 、kV A
4. 视在功率 S。

电源（发电机、变压器等）可能提供的最大功率（额定电压×额定电流）
ϕ U U R U L -U C S=UI
---功率三角形
5 . 有功功率、无功功率与视在功率间的关系
=S U I
视在功率 =Q U I sin ϕ无功功率
=P U I cos ϕ有功功率
---功率三角形 S
Q P 功率三角形 U R
U
+ U U L C 电压三角形
阻抗
三角
形 R X L -X C ϕ
THE END。