高一函数图像变换课件

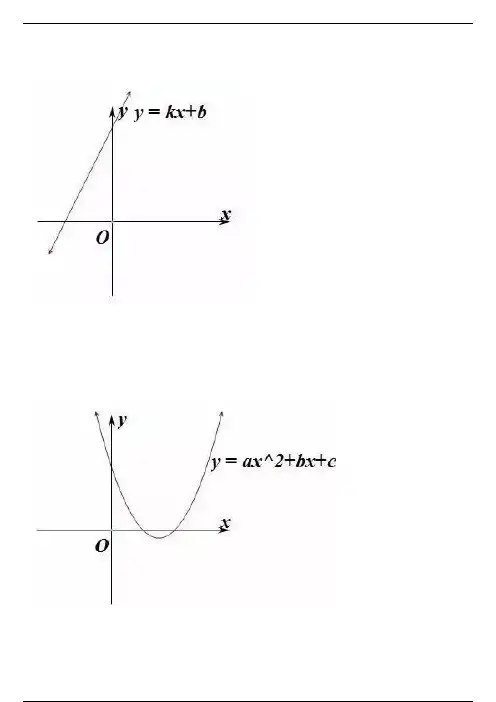
基本初等函数的图像1.一次函数性质： 一次函数图像是直线，当k>0时，函数单调递增；当k<0时，函数单调递减 2.二次函数性质：二次函数图像是抛物线，a决定函数图像的开口方向，判别式b^2-4ac决定了函数图像与x轴的交点，对称轴两边函数的单调性不同。

3.反比例函数性质：反比例函数图像是双曲线，当k>0时，图像经过一、三象限；当k<0时，图像经过二、四象限。

要注意表述函数单调性时，不能说在定义域上单调，而应该说在（-∞，0），（0，∞）上单调。

4.指数函数当0<a<b<1<c<d时，指数函数的图像如下图不同底的指数函数图像在同一个坐标系中时，一般可以做直线x=1，与各函数的交点，根据交点纵坐标的大小，即可比较底数的大小。

5.对数函数当底数不同时，对数函数的图像是这样变换的6.对勾函数对于函数y=x+k/x，当k>0时，才是对勾函数，可以利用均值定理找到函数的最值。

7. 幂函数性质：先看第一象限，即 x>0 时，当 a>1 时，函数越增越快；当0<a<1 时，函数越增越慢；当 a<0 时，函数单调递减；然后当x<0 时，根据函数的定义域与奇偶性判断函数图像即可。

8. 正弦函数、余弦函数、正切函数函数图像的变换 1 平移变换（1）水平平移： 函数 y = f（x + a）的图像可以把函数 y =f（x）的图像沿x轴方向向左（a＞0）或向右（a＜0）平移｜a｜个单位即可得到； （2）竖直平移： 函数 y = f（x） + a 的图像可以把函数 y =f（x）的图像沿x轴方向向上（a＞0）或向下（a＜0）平移｜a｜个单位即可得到。

2 对称变换（1）函数 y = f（-x） 的图像可以将函数 y = f（x）的图像关于y轴对称即可得到； （2）函数 y = - f（x） 的图像可以将函数 y =f（x）的图像关于x轴对称即可得到；（3）函数 y = - f（-x） 的图像可以将函数 y =f（x）的图像关于原点对称即可得到；3 翻折变换（1）函数 y =｜ f（x）｜ 的图像可以将函数 y =f（x）的图像的x轴下方部分沿x轴翻折到x轴上方，去掉x轴下方部分，并保留 y =f（x）的x轴上方部分即可得到；（2）函数 y = f（｜x｜） 的图像可以将函数 y =f（x）的图像的右边沿y轴翻折到y轴左边替代原y轴左边部分并保留 y =f（x）在y轴右边部分即可得到。

函数的图像及变换一、函数图像的变换对称变换(||)翻折翻折变换|()|翻折左右平移平移变换上下平移横坐标不变，纵坐标伸缩伸缩变换纵坐标不变，横坐标伸缩y f x y f x ⎧⎪⎧=⎪⎨⎪=⎩⎪⎪⎧⎨⎨⎪⎩⎪⎪⎧⎪⎨⎪⎩⎩关于x 轴对称：(,)(,)x y x y →- 关于y 轴对称：(,)(,)x y x y →- 关于原点对称：(,)(,)x y x y →-- 关于y x =对称：(,)(,)x y y x →关于y x =-对称：(,)(,)x y y x →-- 关于直线x a =对称：(,)(2,)x y a x y →-（轴对称） 关于y x b =+对称：(,)(,)x y y b x b →-+ 关于y x b =-+对称：(,)(,)x y b y x b →--+ 关于点(,)P a b 对称：(,)(2,2)x y a x b y →--（点对称）例1：已知2()2f x x x =-，且()g x 与()f x 关于点(1,2)对称，求()g x 的解析式.（相关点法）例2：已知函数()y f x =的图像关于直线1x =-对称，且当(0,)x ∈+∞时，有1()f x x=，则当 (,2)x ∈-∞-时，()f x 的解析式是（ ）.A. 1x -B. 12x +C.12x -+D. 12x- 例3：下列函数中，同时满足两个条件“①x R ∀∈，()()01212f x f x ππ++-=；②当6π-<x 3π<时，'()0f x >”的一个函数是（ ） A.()sin(2)6f x x π=+B. ()cos(2)3f x x π=+C. ()sin(2)6f x x π=-D. ()cos(2)6f x x π=-①关于形如()y f x =的图像画法：当0x ≥时，()y f x =；当0x ≤时，()y f x =-()y f x =为偶函数，关于y 轴对称，即把0x ≥时()y f x =的图像画出，然后0x ≤时的图像与 0x ≥的图像关于y 轴对称即可得到所求图像.②关于形如()y f x =的图像画法当()0f x ≥时，()y f x =；当()0f x ≤时，()y f x =-先画出()y f x =的全部图像，然后把()y f x =的图像x 轴下方全部关于x 轴翻折上去，原x 轴上方的图像保持不变，x 轴下方的图像去掉不要即可得到所求图像.例3：画出下列函数的图像.（1）12log y x = （2）228y x x =--例4:设函数2()45f x x x =--.（1）在区间[2,6]-上，画出函数()f x 的图像；（2）设集合{}()5A x f x =≥，(,2][0,4][6,)B =-∞-+∞.试判断集合A B 、之间的关系，并给出证明；（3）当2k >时，求证：在区间[1,5]-上，3y kx k =+的图像位于函数()f x 图像的上方.①左右平移把函数()y f x =的全部图像沿x 轴方向向左（0a >）或向右（0a <）平移a 个单位即可得到函数()y f x a =+的图像②上下平移把函数()y f x =的全部图像沿y 轴方向向上（0a >）或向下（0a <）平移a 个单位即可得到函数()y f x a =+的图像例4：将函数lg(32)1y x =-+按向量(2,3)a =-平移后得到新的图象解析式为 例5:把一个函数的图象按向量(,2)8a π=-平移后得到的图象的解析式为sin(2)24y x π=+-，则原来函数的解析式 .Ⅰ.将函数()y f x =的全部图像中的每一点横坐标不变，纵坐标伸长(1)a >或缩短(01)a <<为原来的a 倍得到函数()(0)y af x a =>的图像.Ⅱ. 将函数()y f x =的全部图像中的每一点纵坐标不变，横坐标伸长(1)a >或缩短(01)a <<为原来的1a倍得到函数()(0)y f ax a =>的图像. 例6：已知函数21()2lg(2)-=++x f x x ，把函数()y f x =的图像关于y 轴对称，然后向右平移1个单位，最后纵坐标保持不变，横坐标变为原来的2倍得到()g x 的图像，求()g x 的解析式.例7：已知函数2()log (1)f x x =+，将()y f x =的图像向左平移1个单位，再将图像上所有点纵坐标伸长到原来的2倍，得到函数()y g x =的图像. （1）求()y g x =的解析式和定义域； （2）求函数()(1)()F x f x g x =--的最大值.【练习】1.为了得到函数321x y -=-的图像，只需要把函数2x y =的图像上所有的点（ ）.A.向右平移3个单位长度，再向下平移1个单位长度B.向左平移3个单位长度，再向下平移1个单位长度C.向右平移3个单位长度，再向上平移1个单位长度D.向左平移3个单位长度，再向上平移1个单位长度 2.下面四个图形中，与函数22log (1)yx x =+≥的图像关于y x =对称的是（ ）.3.若函数()()y f x x R =∈满足(2)()f x f x +=，且[1,1]x ∈-时，()f x x =，则函数()y f x =的图像与函数4log y x =的图像的交点的个数为（ ）.A.3B.4C.6D.84.将函数by a x a=++的图像向右平移2个单位长度后又向下平移2个单位，所得到的函数图像与原图像如果关于直线y x =对称，那么（ ）.A. 1,0a b =-≠B. 1,a b R =-∈C.1,0a b =≠D. 0,a b R =∈ 5.已知21()f x x x =+，且()g x 与()f x 关于点(1,0)-对称，求()g x 的解析式.6.画出下列函数的图像.（1）ln y x = （2）26y x x =--7. 函数()2xf x =和3()g x x =的图像的示意图如图所示，设两函数的图像交于点11(,)A x y ，22(,)B x y ，且12x x <.（1）请指出示意图中曲线12,C C 分别对应于哪一个函数；（2）若12[,1],[,1]x a a x b b ∈+∈+，且{},1,2,3,4,5,6,7,8,9,10,11,12a b ∈，指出,a b 的值，并说明理由；（3）结合函数图像的示意图，判断(6),(6),(2010),(2010)f g f g 的大小关系.8.已知函数()f x 和()g x 的图像关于原点对称，且2()2f x x x =+. （1）求函数()g x 的解析式； （2）解不等式()()1g x f x x ≥--；（3）若()()()1h x g x f x λ=-+在[1,1]-上是增函数，求实数λ的取值范围.6. 已知函数()y f x =，把函数()y f x =的图像向左平移1个单位，然后横坐标保持不变，纵坐标变为原来的3倍再向下平移3个单位得到()g x 的图像，求()g x 的解析式.补充：请把相应的幂函数图象代号填入表格.①32x y =；②2-=x y ；③21x y =；④1-=x y ；⑤31x y =；⑥23x y =；⑦34x y =； ⑧21-=x y ；⑨35x y =.常规函数图像有：函数代号 ①②③④⑤⑥⑦⑧⑨⑩图象代号HI指数函数：逆时针旋转，底数越来越大 .对数函数：逆时针旋转,底数越来越小幂函数：逆时针旋转，指数越来越大。

函数图像的变换1、平移变换函数y = f(x)的图像向右平移a个单位失掉函数y = f(x - a)的图像;向上平移b个单位失掉函数y =f(x)+ b 的图像 ;左平移a个单位失掉函数y = f(x + a)的图像;向下平移b个单位失掉函数y =f(x)- b 的图像(a ，b&gt;0)。

2、伸缩变换函数 y = f(x)的图像上的点坚持横坐标不变纵坐标变为原来的k倍(01时，伸)失掉函数 y = k f(x)的图像;函数 y = f(x)的图像上的点坚持纵坐标不变横坐标变为原来的1/k倍(01时，缩)失掉函数y = f(k x)的图像(k&gt;0，且 k &ne;1)。

3、对称变换(1)函数y = f(x)的图象关于y轴对称的图像为 y =f(-x);关于x轴对称的图像为y =-f(x);关于原点对称的图像为y =-f(-x)。

(2)函数y = f(x)的图象关于x=a对称的图像为y=f(2a-x);关于y=b对称的图像为y =2b-f(x);关于点(a，b)中心对称的图像为y =2b-f(2a-x)。

(3)相对值效果①函数 y =f(x)x轴及其上方的图像坚持不变，把下方图像关于x轴对称的翻折到上方，再把下方的图像去掉失掉函数 y =| f(x)|的图像;②函数 y =f(x)y轴及其右侧的图像坚持不变，把左侧图像去掉，再把右侧图像关于y轴对称的翻折到左侧失掉函数 y =f(| x|)的图像;③函数y = f(x)先用第②步的方法失掉函数y =f(| x|)的图像，再平移a个单位失掉函数y =f(|x-a|)图象。

我们还可以失掉下面的结论：(1)函数y = f(x)与y =f(2a-x)图象关于直线x = a 对称;(2)函数y = f(x)与y =2b-f(x)图象关于直线y = b 对称;(3)函数y = f(x)与y =2b-f(2a-x)图象关于点(a，b)对称;附注：下面是有关函数图象自身的对称性的一些结论，我们把它放在这里来对比一下：(1)假定函数 f(x)满足：对恣意的实数x，都有f(a + x)=f(a -x)成立，那么函数 f(x)的图像关于x=a对称;(2)假定函数 f(x)满足：对恣意的实数x，都有f(bx)=f(2a -bx)成立，那么函数 f(x)的图像关于x=a对称;(b&ne;0)(3)假定函数 f(x)满足：对恣意的实数x，都有f(a + x)=-f(a -x)成立，那么函数 f(x)的图像关于点(a,0)对称;(4)假定函数 f(x)满足：对恣意的实数x，都有f(bx)=-f(2a -bx)成立，那么函数 f(x)的图像关于(a,0)对称;(b&ne;0)(5)假定函数 f(x)满足：对恣意的实数x，都有f(a + x)=2b -f(a -x)成立，那么函数 f(x)的图像关于点(a,b)对称;(6)假定函数 f(x)满足：对恣意的实数x，都有f(x)=2b -f(2a -x)成立，那么函数 f(x)的图像关于(a,b)对称。