高中数学比赛课件：函数图像的变换课件

格式：ppt
大小：1.30 MB
文档页数：15

下载文档原格式

函数图的变换-PPT课件

1 个单位平移 ____
选（ D ） . y sin( 2 x ) sin 2 ( x )
（） (A) 向左平移个单位（B) 向右平移个单位 3 3 （C）向右平移个单位（D）向右平移个单位 6 6
菜单
例 3 、函数 ylog 1 |当 x ( 1 ,0 ) 时总有 a|x y0 ,那么函数的单调递增区间是（）
2
f (x) f ( x), 而（-1，1）与（1，1）（-2，4）与（2，4） ..... （-x,y）与（x,y）都是关于y轴对称的！所以才有函数图象本身关于y轴对称!
而
y x3或 y x5 : f (1 ) f (1 ) 1 , f (2) f (2)..... f (x) f (x) y. 因为（ -1， -1）与（ 1， 1） (-2,-8)与 (2,8)(-x,-y)与 (x,y)关于原点对称所以整个图象关于原点对称 !
Y
X
例 3 、函数 ylog 1 |当 x ( 1 ,0 ) 时总有 a|x y0 ,那么函数的单调递增区间是（ D）
( A )( , 0 ) ( C )( 0 , )
( B )( , 1 ) ( D )( 1 , )
左移 1 单位沿 y 轴翻折 y log |x 1 | y log x y log | x | a a a
x ,n 为奇数这样的函数我们称为奇函数,形如 y
1)a>1时 2)0<a<1时
Y
X 菜单
例4函数y=f(1-x)与函数y=f(x-1)的图象的对称轴方程为（ C ）（A)x=0 (B)y=0 (C)x=1 (D)x=-1

教A版高中数学必修一1.2.2 函数的图像变换(共37张PPT)

函数 y loga x与y log 1 x loga x 的图象关于x轴对称
a
y
点（X,-Y)与(X，Y)
关于X轴对称 y log2 x
谁不变关
于谁对称
O
y log3 x
y log1 x x
3
一般地，y=f(x)与y=-f(x)的图象关于
y log1 x
2
x轴对称；
例3.①画函数 g(x) x2 2 | x |的图象，并说明
解：f (x) x 3 (x 2) 1 1 1 1 1
x2 x2
x2 x2
f (x) x 3 的图象是由函数g(x) 即1：的f图(象 x) g(x 2) 1
x2
x
向左平移2个单位，再向上平移1个单位得到。
其对称中心为（- 2,1）
观察下面指数函数的图象
得到：y a x与y ( 1 ) x a x (a 0且a 1)的 a
y=f(x)沿x轴 y=f(x+a)
当a>0时，向左平移a个单位当a<0时，向右平移|a|个单位
规律：左加右减
例2：画出下列函数的图象, 并说明它们的关系:
(1) f(x)=x2 (2) g(x)=x2+2 (3) h(x)=x2－2
8
7
g(x) x2 2
6
又 g(x) f (x) 2
翻折到y轴左侧，便得到g(x) x2 2 | x | f (| x |)的图象，
（2）画函数h(x) | x2 2x |的图象，并说由函数
f (x) x2 2x的图象怎样变换而得到？
解析：h(
x)
x2
x
2
2x (x 2x (0

高一必修1-函数图象的变换ppt课件.ppt

如:y=f(x)±h的图象可由y=f(x)的图象 _向__上__（__下__）__平__移__h_个__单__位__而得到.
练习：将直线y=2x+1向左平移5个单位，
得到的函数为__y_=_2_x+_1_1_______
左右平移时，发生变化的仅是x本身，如果x的系数不是1时，需要把系数提出来，再进行变换.
(6)y=f(|x|)的图象:可先作出y=f(x)当x≥0 时的图象,再利用_偶__函__数__的__图__象__关__于__y_轴__对__称, 作出y=f(x)(x≤0)的图象.
函数y=|log2x|的图象是( A )
解析
f
(x)
|
lo g2
x
|
lo g2
lo
g1
2
x, x x,0
1, x
课前练习：
当a>2时,函数 y ax和y (a 1)x2 的图象只可能是( )
y
y
y
y
0
x
A
0
x
B
0x
C
0x
D
知识回顾：基本初等函数及图象（大致图象）
函数一次函数 y=kx+b
图象
二次函数
y=ax2+bx+ c
指数函数 y=ax
对数函数 y=logax
知识回顾：
下列二次函数的图象，是由抛物线y=x2通过怎样的平移变换得到的？
y f 1(x) 与y=f(x)的图象关于直线y=x对称.
设奇函数 f(x) 的定义域为[-5, 5], 若当x∈[0, 5]时, f(x)的图象如右图所
示. 则不等式 f(x)<0 的解集
是 (-2, 0)∪(2, 5]

函数图像变换ppt课件

横坐标取相反数纵坐标不变
y=f(x)与y=f(-x)图象关
横坐标、纵坐标同时取相反数
y=f(x)与y=-f(-x)图象
对称变换Biblioteka 于y轴对称关于原点对称
问题2：说出下列函数的图象与指数函数y=2x的图象的关系，并画出它们的示意图. (4)y=log2x (3)y=-2-x (1)y=2-x (2)y=-2x
2 x (x1 )1 1 1 y x 1 x 1 x1
1 y x x换成x-1
1 y x 1
向右平移1个单位
y
O
1 -1
（1，-1）
x
向下平移1个单位
1 y 1 x 1
例3.已知函数y=|2x-2| （1）作出函数的图象；（2）指出函数的单调区间；（3）指出x取何值时，函数有最值。
y y y y
1
O
1 1 x
O
1 x -1
O
-1
x
O1
x
（x,y)和(-x,y) 关于y轴对称！（x,y)和(y,x) y 轴y=x 与和 y=f(-x) 的图象关于对称；关于直线对（ x,y)和(-x,-y) 对（1）y=f(x) （x,y) (x,-y) 称！关于原点对称！ x 轴对称；与 y=-f(x) 的图象关于关于x 轴对称！称（2）y=f(x) 变（3）y=f(x)与y=-f(-x)的图象关于原点对称；
y=f(x-1) 1 -1 O 1
x
y=f(x)-1 -1
a>0,向左平移a个单位 y=f(x+a)左右平移 a<0,向右平移|a|个单位 k>0,向上平移k个单位 y=f(x)+k 上下平移 k<0,向下平移|k|个单位

函数图像的变换PPT

总结词
当函数图像在y轴方向上伸缩时，其形状和位置会发生变化，但对称性保持不变。
详细描述
沿y轴伸缩是指保持x轴不变，只改变y轴的长度。当y增大时，整个函数图像向上平移；当y减小时，整个函数图像向下平移。这种变换不会改变函数的值，只是改变了图像在y轴上的位置。
同时沿x轴和y轴伸缩
总结词
当函数图像在x轴和y轴方向上都发生伸缩时，其形状和位置会发生变化，但对称性保持不变。
03
伸缩变换
沿x轴伸缩
总结词
当函数图像在x轴方向上伸缩时，其形状和位置会发生变化，但对称性保持不变。
详细描述
沿x轴伸缩是指保持y轴不变，只改变x 轴的长度。当x增大时，整个函数图像向右平移；当x减小时，整个函数图像向左平移。这种变换不会改变函数的值，只是改变了图像在x轴上的位置。
沿y轴伸缩
详细描述
旋转角度的大小对函数图像的形状和位置有直接影响。例如，当一个正弦函数图像顺时针旋转90度时，它将变成一个余弦函数图像；而当它逆时针旋转90度时，它将变成一个正切函数图像。此外，旋转角度也会影响图像的位置，例如，当图像逆时针旋转30度时，图像上的所有点都会沿着顺时针方向移动
30度。
旋转变换实例
总结词
旋转变换是指函数图像绕原点旋转的过程。
详细描述
旋转变换可以通过将直角坐标转换为极坐标来实现。例如，函数$y = f(x)$的图像绕原点逆时针旋转$theta$角度后，新的函数可以表示为$y = f(rcostheta), x = rsintheta$。
复合变换实例
总结词
复合变换是指同时进行平移、伸缩和旋转变换的过程。
与顺时针旋转相反，如果函数图像按照逆时针方向旋转，那么图像上的每一个点都会沿着顺时针方向移动。例如，如果一个函数图像是关于x轴对称的，那么当它逆时针旋转90度时，原来的对称轴将变成垂直轴，而原来的y 轴将变成水平轴。

高一数学图象变换ppt课件

y f( x )
保留x轴上方图像，再将x轴
下方图像对称翻折到x轴上方
y f(x)
练习3：
分别作出下列函数的图像：
2 4 x 3 1、 yx
2、
2 yx 4 x 3
保留x轴上方图象，再将x轴 2 2 y x 4 x 3 解： y x 4 x 3 1、下方图像对称翻折到x轴上方
1.将函数y=f(x)图象保留x轴上方的部分并且把x轴下方的部分关于x轴作对称就得到函数 y=|f(x)|的图象 2.将函数y=f(x)图象去掉y轴左方的部分，保留y轴右方的部分并且把它关于y轴作对称就得到函数y=f(|x|)的图象
思考：求方程 x 4 x 3 m 的根的个数。
61 1 3x 7 3x 3 解：y x2 x 2 x2
好象学过怎么办呢？ 1 … y 的图象！ x
y
1 y x
平移变换
o
x
1 y 因此：我们可将函数的图象先沿x轴向左平移2个单位，再 x 1 沿y轴向上平移3个单位得到函数 y 3 的图象。 x2
1 y 3 x 2
3 () 3 3 3 y 3
y 3x 向左移1个单位 y 3x1
或： y 3
y
x
关于y轴对称
向右移1个单位
y
y 3x1
( x 1 ) x 1 y 3 3
关于y轴对称
y 3
x
y 3
x
4 3
4 3 2
y 3x
x 1 y 3 1,1
y f( x )
小结：对称变换
1.函数y=f(-x)与函数y=f(x)的图象关于y轴对称.

函数图像的变换优秀课件

函数图像的变换优秀课件
平移变换—水平平移
f(x+2)=(x+2)2
y f(x)=x2
-2 O
f(x-2)=(x-2)2
2
x
ቤተ መጻሕፍቲ ባይዱ
平移变换—水平平移
小结：
y=f(x) 沿 x轴
y=f(x+a) 当a>0时，向左平移 a个单位当a<0时，向右平移
|a|个规单律位：左加右减
平移变换—竖直平移 y=x2 +1
1 1 , 1 0,1 2
-4 -3 -2 -1 0 1 2 3 4 x
-1
y (1) x 2
-2
-3
y
4
y log2x
3
y log2x1
-4 -3 -2 -1
2
1,1
1
4,2 4,1
1,0
x 0 1 2 1 , 1 3 4
-1 2 1,1
ylog2x1
-2 1 , 2 2
（x,y)换成（x,-y)
1、 y f (x) 关于y轴对称 yf(x) 3、y f (x) 关于原点对称 yf(x)
（x,y)换成（-x,y)
（x,y)换成（-x,-y)
三、适应练习Ⅰ
1、y x2 与 y x2 的图像关于______x__轴_____对称；
2、 f (x)2x1 与g(x)21x的图像关于_____y__轴______对称；
y f(x)=x2
1
O -1
y=x2 -1 x
平移变换—竖直平移
小结：
y=f(x)沿 y轴 y =f(x) +a
当a>0时，向上平移a个单位当a<0时，向下平移|a|个单位

高中数学《函数图象的变换》课件

将y = f(x)在 x 轴上方的图象保留，下方的图象以 x 轴为对称轴翻折到上方可得到 y =|f(x)| 的图象.（保上方，下方翻上方）
翻折变换
y = f(x) 的图象
y =|f( x )| 的图象
将y = f(x)在 x 轴上方的图象保留，下方的图象以 x 轴为对称轴翻折到上方可得到 y =|f(x)|的图象.
平移变换
左上右下平平移移
对称变换
关关关于于于 x y原轴轴点
翻折变换
上左下右翻翻折折
归纳总结
平 y = f(x) 左移 h (h>0) y = f(x + h)
移的图象个单位
的图象
变换
y = f(x) 右移 h (h>0) y = f(x - h)
的图象个单位
的图象
问题与思考——复习
1、在同一坐标系中作下列函数的图象，并说明每组两函数图象间的关系.
(1) y = |log2x| (2) y = x2 - 2x，y = |x2 - 2x|
yy= log2 x
o
o
1
x
1
x
将 y = log2x 在 x 轴上方的图象保留，下方的图象以 x 轴为对称轴翻折到上方可
翻的图象折变换
y =f( |x| ) 的图象
？
谢谢
翻折变换
问题与思考：
2、在同一坐标系中作下列函数的图象，并说明每组两函数图象间的关系.
(1) y = 2x，y = 2|x| (2) y = x2 - 2x，y = |x|2 - 2|x|
y
y
y = 2x 11
o x
y = 2|x| 1

高中数学：131《三角函数图像的变换》课件必修

这些操作包括平移、伸缩、翻折和旋转等，可以单独或组合使用。
变换的目的是为了更好地理解三角函数的性质，解决实际问题，以及进行图像处理等。
变换的种类和特点
01
02
03
04
平移变换
将图像沿x轴或y轴方向移动，保持图像形状不变。
伸缩变换
通过改变x轴和y轴的比例来改变图像的大小，可以横向或
纵向伸缩。
翻折变换
利用伸缩变换的性质求解函数的极值
例如，利用正弦函数的伸缩性质，可以求解y=sin(3x)在x=π/9处的极小值为1。
利用对称变换的性质求解函数的对称轴或对称中心
例如，利用正弦函数的对称性质，可以求解y=sin(x)的对称轴为x=kπ+π/2，k∈Z。
变换在实际问题中的应用
物理学中的应用
三角函数图像的综合变换在物理学中有广泛的应用，如振动和波动现象、交流电等。通过变换可以更好地理解物理现象和解决实际问题。
x轴缩短为原来的1/2，则图像的周期变为原来的2倍。
01
03
02 04
总结词：影响相位
详细描述：沿x轴伸缩不仅改变了图像的周期，还会影响函数的相位。例如，将x轴缩短为原来的1/2，相当于将相位滞后了π。
沿y轴伸缩
总结词：改变振幅
详细描述：沿y轴伸缩是指保持x轴不变，通过改变y轴的长度来改变整个图像的振幅。例如，将y 轴放大为原来的2倍，则图像的振幅变为原来的2 倍。
翻折变换
旋转变换
$y = -f(-x)$ 或 $y = f(x)$，前者表示沿x 轴翻折，后者表示沿y轴翻折。
$x = xcostheta - ysintheta$ 和 $y = xsintheta + ycostheta$，其中$theta$为旋转角度。

函数图像及其变换PPT优秀课件

从图象的左右分布，分析函数的定义域；从图象的上下分布，分析函数的值域；从图象的最高点、最低点，分析函数的最值、极值；从图象的对称性，分析函数的奇偶性；从图象的走向趋势，分析函数的单调性、周期性等．
1．要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、三角函数等各种基本初等函数的图象．
(1)y＝|xx3|；(2)y＝xx＋－21； (3)y＝|log2x－1|；(4)y＝2|x－1|.
【解析】
(1)y＝x－2 x2
(x＞0) (x＜0)
，利用二次
函数的图象作出其图象，如图①.
(3)先作出y=log2x的图象，再将其图象向下平移一个单位，保留x轴上及x轴上方的部分，
将x轴下方的图象翻折到x轴上方，即得 y=|log2x-1|的图象，如图③.
(4)选择描点法或图象变换法作出相数图象要标出特殊的线(如渐近线)和特殊的点，以显示图象的主要特征，处理这类问题的关键是找出基本函数，将函数的解析式分解为只有单一变换的函数链，然后依次进行单一变换，最终得到所要的函数图象．
作出下列函数的大致图像：
(4)先作出y=2x的图象，再将其图象在y轴左边的部分去掉，并作出y轴右边的图象关于y轴对称的图象，即得y=2|x|的图象，再将y=2|x|的图象向右平移一个单位，即得y=2|x-1|的图象，如图④.
由图象求解析式
如图所示，函数的图象由两条射线及抛物线的一部分组成，求函数解析式．
【思路点拨】分段求函数解析式，再合成分段函数形式，本题分别设为一次函数和二次函数形式，应抓住特殊点 (0,2)，(1,1)，(2,2)，(3,1)和(4,2)．
函数图像及其变换
1．几种函数的图像函数

函数图象的变换PPT

总结词
水平平移是指函数图像在水平方向上移动一定的距离。
详细描述
水平平移不改变函数的值，只是改变了图像的位置。对于函数y=f(x)，若图像向右平移a个单位，则新的函数为y=f(x-a)；若图像向左平移a个单位，则新的函数为y=f(x+a)。
垂直平移
总结词
垂直平移是指函数图像在垂直方向上移动一定的距离。
函数图象的变换
• 函数图象变换概述 • 平移变换 • 伸缩变换 • 翻折变换 • 旋转变换 • 应用实例
01
函数图象变换概述
函数图象变换的定义
01
函数图象变换是指通过平移、伸缩、翻转等几何变换操作，改变函数图象的位置、形状和大小。
02
这些变换操作可以通过代数表达式或矩阵变换来实现，使得函数图象在坐标系中按照特定的规则进行移动、旋转和缩放。
详细描述
当函数图像在y轴方向上伸缩时，其形状和大小会发生变化，但x轴上的比例保持不变。例如，将函数y=f(x)的图像在y轴方向上放大2倍，得到新的函数y=2f(x)。
斜向伸缩
要点一
总结词
斜向伸缩是指同时沿x轴和y轴方向对函数图像进行放大或缩小。
要点二
详细描述
当函数图像在x轴和y轴方向上同时伸缩时，其形状和大小会发生变化，x轴和y轴上的比例都会改变。例如，将函数 y=f(x)的图像在x轴方向上放大2倍，在y轴方向上放大3倍，得到新的函数y=3f(2x)。
逆时针旋转
总结词
当函数图像按照逆时针方向旋转时，其形状和大小也不会发生变化，同样只是位置发生了移动。
详细描述
与顺时针旋转相反，当函数图像按照逆时针方向旋转一定的角度时，每个点的坐标同样会发生变化，但方向是远离原点。同样地，这种变化也可以用三角函数的性质来描述。

函数图像的变换课件

向右平移
总结词
图像沿x轴正方向移动
数学表达式
y=f(x-a)
详细描述
对于函数y=f(x)，若图像向右平移a个单位，则新的函数解析式为y=f(x-a)。
举例
函数y=cos(x)的图像向右平移π/2个单位后，得到新的函数y=cos(x-π/2)，其图像与原图像相比沿x轴正方向移动了π/2个单位。
双向伸缩
总结词
同时改变x轴和y轴的长度。
详细描述
当函数图像在x轴和y轴方向上都发生伸缩时，x轴和y轴的长度都会发生变化。这种变换可以通过将函数中的x和y都替换为其倍数来实现，例如将f(2x)/3替换为 f(x)会使x轴压缩为原来的一半，同时y轴拉伸为原来的三倍。
04
函数图像的旋转变换
逆时针旋转
关于y轴对称
总结词
函数图像关于y轴对称时，图像在y轴两侧对称分布，x值不变，y值相反。
详细描述
当一个函数图像关于y轴对称时，图像在y轴两侧呈现出对称分布的特点。这意味着对于任意一个点$(x, y)$在图像上，关于y轴对称的点$(x, -y)$也在图像上。这种对称变换不会改变x值，只是将y值取反。例如，函数$f(x) = x^3$的图像关于y轴对称，因为$f(-y) = (-y)^3 = -y^3 = -f(y)$。
任意角度旋转
总结词
任意角度旋转是指将函数图像按照任意角度进行旋转。
详细描述
任意角度旋转函数图像是指将图像上的每个点都按照任意指定的角度进行旋转。这种旋转可以通过参数方程或极坐标系来实现，其中参数方程为$x = x cos theta - y sin theta$，$y = x sin theta + y cos theta$，极坐标系下的表示为$x = r cos theta$，$y = r sin theta$。

函数的图象及变换省公开课获奖课件说课比赛一等奖课件

高考第一轮复习
考点16 函数旳图象及变换
一、知识要点
周期性
定义域解析式
性质
奇偶性
单调性
x轴 y轴
原点 y=x
y=－x
x=a
直线 x=a 直线 x=a
解析：措施一：设(x1，y1)是y＝f(x－a)图像上任意一点，则y1＝f(x1－a)，而f(x1－a)＝f[a－ (2a－x1)]，阐明点(2a－x1，y1)－定是函数y＝f(a －x)上旳一点，而点(x1，y1)与点(2a－x1，y1)有关直线x＝a对称，所以y＝f(x－a)旳图像与y＝f(a －x)旳图像有关直线x＝a对称，所以选D.
当a＞1时，如图，要使在(1,2)上，f1(x)＝(x－ 1)2旳图像在f2(x)＝logax旳下方，只需f1(2)≤f2(2)．
即(2－1)2≤loga2，loga2≥1，∴1＜a≤2.
规律措施：从常见函数旳图像入手，巧妙地利用图像与不等式(方程)之间旳关系，将不等式 (方程)转化为求函数图像旳交点问题，数形结合是处理此类题旳有效措施．
【预测4】已知函数f(x)＝|x2－4x＋3|. (1)求函数f(x)旳单调区间； (2)求m旳取值范围，使得方程f(x)＝mx有四个不等实根．
f(x)旳图像如图所示．函数f(x)旳单调区间有(－∞，1]、 [1,2]、[2,3]、[3，＋∞)，其中增区间有[1,2]、[3，＋∞)，减区间有(－∞，1]、[2,3]．
答案：A
规律措施：注意从f(x)，g(x)旳奇偶性、单调性等方面寻找f(x)·g(x)旳图像特征．
【预测2】 (1)已知函数y＝f(x)旳图像如图① 所示，y＝g(x)旳图像如图②所示，
则函数y＝f(x)·g(x)旳图像可能是下图中旳 ()

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

y f(x)
保留x轴上方图像，再将x轴下方图像对称翻折到x轴上方
y f (x)
2、用图像变换法画函数图像时，往往要找出该函数的基本初等函数，分析其通过怎样变换得到所求函数图像，有时要先对解析式进行适当变形。
3、利用函数的图像判定单调性、求方程根的个数、解不等式、求最值等，体现了数形结合的数学思想。
函数图像的翻折变换规律：
由 y f (x) 保留y轴右侧图像，再将y轴
右方图像对称翻折到y轴左方
y f (x)
由 y f (x) 保留x轴上方图像，再将x轴
下方图像对称翻折到x轴上方
y f (x)
五、适应练习Ⅱ
分别作出下列函数的图像：
1、 y x2 4x3
2、 yx24x3
解：1、 yx24x3
y=a(a<0) 没有交点
-3 -2 -1
01 2 3 x -1
-2
y=a(a=0)
有两个交点
-3
-4
七、抽像概括
1、图像变换法：
（1）对称变换法
（2）翻折变换法
yf(x)
关于y轴对称
yf(x)
关于x 轴对称
y
f (x)
关于直线 y f 1(x)
y＝x对称
关于原点对称
yf(x)
y f (x)
保留y轴右侧图像，再将y轴右方图像对称翻折到y轴左方
现形式哦!
3,0
2
1,0 1 1,0 3,0
01 2 3 4 x
-4 -3 -2 -1 0 1 2 3 4 x
-1 2,1
2,1 -1 2,1
-2
-2
-3 yx24x3
yx24x3 -3
图1
图2
六、实例讲解
例1、作出下列函数的图像，并指出函数的定义域、值域、奇偶性、单调性：
1、 y ( 1 ) x 2
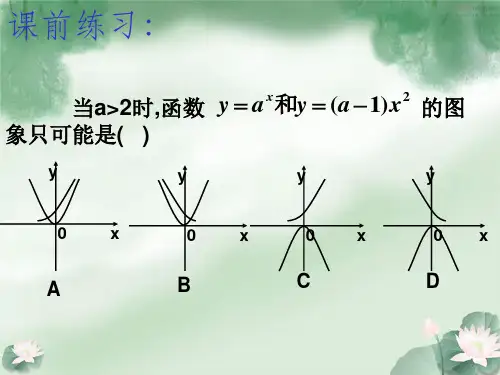
高中数学比赛课件：函数图像的变换课件
一、教材分析
四、教学方法
二、教学重点、难点五、教学过程
三、教学目标
六、教材设计说明
一、新课引入
函数图像的平移变换规律：本质上是函数图像上的每个点的平移
y f(x) y f(x)
yf(xa)
a 0
a0
向左平移 a个单位左右平移
向右平移
a
个单位
解：在同一坐标系中，作出 y=|x2+2x-3|和y=a 的图像。
由图可知：
y=a(a=4) 有三个交点
y=a(0<a<4) 有四个交点
y=a(a>4) y 有二个交点
4 3 2 1
当a<0时, 方程无解; 当a=0时, 方程有两个解;
当0<a<4时, 方程有四个解; 当a>=4或时a，=0方时程,方有程三有个两解个; 解. 当a>4时, 方程有两个解.
保留x轴上方图像，再将x轴下方图像对称翻折到x轴上方
y x2 4x3
2、 yx24x3
保留y轴右侧图像，再将y轴右 yx2 4x3
方图像对称翻折到y轴左方
y
4 y x2 4x3
注意区分
yx24x3
y
4
0,3 3
y f ( x)与
0,3 3
-4 -3 -2 -1
2
2,1
1
1,0 3,0
y f (x)的表
（x,y)换成（x,-y)
1、 y f (x) 关于y轴对称 yf(x) 3、y f (x) 关于原点对称 yf(x)
（x,y)换成（-x,y)
（x,y)换成（-x,-y)
三、适应练习Ⅰ
1、 y x2 与 y x2 的图像关于______x__轴_____对称；
2、 f (x)2x1 与 g(x)21x的图像关于______y__轴_____对称；
函数定义域
y (1)x 2
R
y log2x1 {x| x0}
值域
(0,1] [0,)
奇偶性
偶非奇非偶
单调性
增区（ : ,0 间）减区（ :0 ，间）增区（ :2,间）减区（ :0， 2）间
六、实例讲解
例2：求关于x的方程 x22x3a(aR) 的不同实根的个数。
3
右方图像对称翻折到y轴左方 y (1) x
2
2
1,1
1
1,0
4,2 4,1
2、y log2x
向下移1 个单位
ylog 1 x 0 1 2 1 ,1 3 4
保留x轴上方图 -1 2 1,1
ylog2x1
x 2
像，再将x轴 -2 1 , 2 下方图像对称翻 2
-3
折到x轴上方 y log2x1
你能得出什么结论？
y
4 3
y 2x
2
y 2x
1
-2 -1 0 1 2 x
-1
-2
-3
y
4
3
y 2x
2
1
-2 -1 0 1 2 x
-1
y 2x -2
-3
y4
3 2 1
y 2x
-2 -1
01 2 x
-1
-2 y 2x
-3
关于y轴对称
关于x轴对称
关于原点对称
函数图像的对称变换规律：
2、y f (x) 关于x轴对称 yf(x)
左加右减
yf(x)k
k 0
k
0
向上平移 k 个单位上下平移
向下平移
k
个单位
上加下减
问题思考：
1、如何由函数 y 3x 的图像得到函数 y 3(1)x 的图像？ 3
2、如何由函数 yx24x3的图像作出函数 y x2 4x3 的图像？
二、问题探究Ⅰ
在同一坐标系下作出函数 y 2x 与 y 22xxx，的图像，观察函数图像的特征，
2、 y log2x1
解：1、 y ( 1 ) x
2 保留y轴右侧图像，再将y轴
y
4
1,2
3
y (1)x
2
2
1, 1 2
1 1 , 1 0,1 2
-4 -3 -2 -1 0 1 2 3 4 x
-1
y (1) x 2
-2
-3
y y log2x1
-4 -3 -2 -1
4 y log2x
ylog2x
y
4
3 y log2x2y4 y log2x
3
2
1
1,0 1,0
-4 -3 -2 -1 0 1 -1
-2
-3
2 34 x
y log2 x
-4 -3 -2 -1
y log2x
1
1,0
01 2 3 4 x
-1
-2 -3
ylog2x
ylo2gx lloo2g2gxx((xx00))
ylo2gx lloo2g2xgx(0(xx1 )1)
3、如何由函数 y 3x 的图像得到函数 y 3(1)x 的图像？
解：
y3(1)x33x3x1
3
3
y 3x 向左移1个单位 y 3x1 关于y轴对称 y 3x1
或：y 3x 关于y轴对称 y 3x 向右移1个单位 y3(x1) 3x1
y
4 3
y 3x
y 3x1 1,1
2
10,11,1
y 3x1
-4 -3 -2 -1 0 1 2 3 4 x
-1
-2
-3
y 3x
y
4 3
y 3x
2
01,1 1,1
y 3x1
-4 -3 -2 -1 0 1 2 3 4 x
-1
-2
-3
注意：当自变量的系数为负时，注意平移变换的方向
四、问题探究Ⅱ
画出函数 yy lloog22x 的图像，并指出它与 y log2x 的图像有何联系？
八、课外作业
1、试画出下列函数的图像：
（1） y 21x ；
（2） y
1 x 1.
2、求方程的 lgx x30 实数解的个数。
谢谢观赏！
2020/11/5
15