高一函数图像变换课件

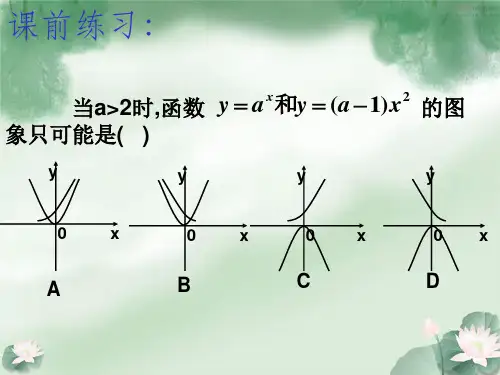
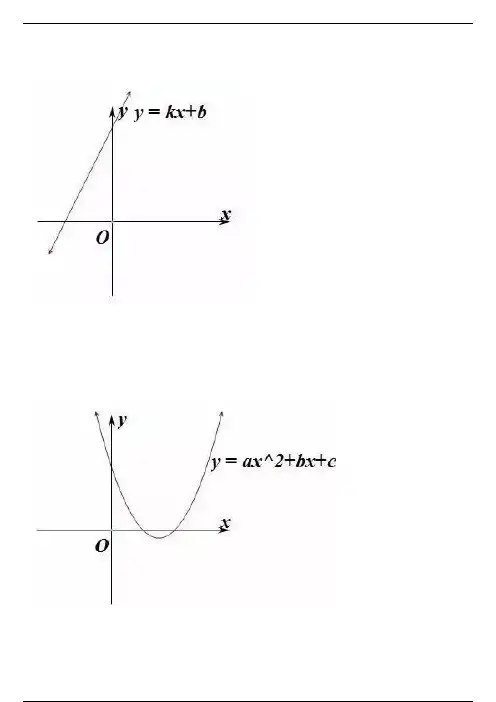
基本初等函数的图像1.一次函数性质： 一次函数图像是直线，当k>0时，函数单调递增；当k<0时，函数单调递减 2.二次函数性质：二次函数图像是抛物线，a决定函数图像的开口方向，判别式b^2-4ac决定了函数图像与x轴的交点，对称轴两边函数的单调性不同。

3.反比例函数性质：反比例函数图像是双曲线，当k>0时，图像经过一、三象限；当k<0时，图像经过二、四象限。

要注意表述函数单调性时，不能说在定义域上单调，而应该说在（-∞，0），（0，∞）上单调。

4.指数函数当0<a<b<1<c<d时，指数函数的图像如下图不同底的指数函数图像在同一个坐标系中时，一般可以做直线x=1，与各函数的交点，根据交点纵坐标的大小，即可比较底数的大小。

5.对数函数当底数不同时，对数函数的图像是这样变换的6.对勾函数对于函数y=x+k/x，当k>0时，才是对勾函数，可以利用均值定理找到函数的最值。

7. 幂函数性质：先看第一象限，即 x>0 时，当 a>1 时，函数越增越快；当0<a<1 时，函数越增越慢；当 a<0 时，函数单调递减；然后当x<0 时，根据函数的定义域与奇偶性判断函数图像即可。

8. 正弦函数、余弦函数、正切函数函数图像的变换 1 平移变换（1）水平平移： 函数 y = f（x + a）的图像可以把函数 y =f（x）的图像沿x轴方向向左（a＞0）或向右（a＜0）平移｜a｜个单位即可得到； （2）竖直平移： 函数 y = f（x） + a 的图像可以把函数 y =f（x）的图像沿x轴方向向上（a＞0）或向下（a＜0）平移｜a｜个单位即可得到。

2 对称变换（1）函数 y = f（-x） 的图像可以将函数 y = f（x）的图像关于y轴对称即可得到； （2）函数 y = - f（x） 的图像可以将函数 y =f（x）的图像关于x轴对称即可得到；（3）函数 y = - f（-x） 的图像可以将函数 y =f（x）的图像关于原点对称即可得到；3 翻折变换（1）函数 y =｜ f（x）｜ 的图像可以将函数 y =f（x）的图像的x轴下方部分沿x轴翻折到x轴上方，去掉x轴下方部分，并保留 y =f（x）的x轴上方部分即可得到；（2）函数 y = f（｜x｜） 的图像可以将函数 y =f（x）的图像的右边沿y轴翻折到y轴左边替代原y轴左边部分并保留 y =f（x）在y轴右边部分即可得到。

三角函数第七课 §三角函数图像变换复习：指出y = sin x 的图像变换为)32sin(π+=x y 的图像的两种方法平移法过程：两种方法殊途同归(1) y=sinx相位变换y=sin(x+φ)周期变换y=sin(ωx+φ)振幅变换 )sin(ϕ+ω=x A y (2)y=sinx 周期变换y=sin ωx 相位变换y=sin(ωx+φ)振幅变换)sin(ϕ+ω=x A y三种变换： 1. 平移变换①对“x ”左加右减; ②对“y ”上加下减。

2. 翻折变换 ①关于x 轴翻折 ②关于y 轴翻折 ③关于原点翻折 ④对“x ”加绝对值 ⑤对“y ”加绝对值 3. 伸缩变换②周期变换巧求初相角，最高点法例题如图，它是函数y ＝A sin(ωx ＋ϕ)(A ＞0，ω＞0)，｜ϕ｜＜π的图象，由图中条件，写出该函数解析式.练习：1.(1)y ＝sin(x ＋4π)是由y ＝sin x 向 平移 个单位得到的. (2)y ＝sin(x －4π)是由y ＝sin x 向 平移 个单位得到的. (3)y ＝sin(x －4π)是由y ＝sin(x ＋4π)向 平移 个单位得到的.2.要得到函数y ＝sin(2x －3π)的图象，只须将函数y ＝sin2x 的图象 A.向左平移3πB.向右平移3πC.向左平移6πD.向右平移6π3.若将某函数的图象向右平移2π以后所得到的图象的函数式是y ＝sin(x ＋4π)，则原来的函数表达式为( )A.y ＝sin(x ＋43π) B.y ＝sin(x ＋2π) C.y ＝sin(x －4π) D.y ＝sin(x ＋4π)－4π4.将函数y ＝f (x )的图象沿x 轴向右平移3π，再保持图象上的纵坐标不变，而横坐标变为原来的2倍，得到的曲线与y ＝sin x 的图象相同，则y ＝f (x )是( )A.y ＝sin(2x ＋3π)B.y ＝sin(2x －3π)C.y ＝sin(2x ＋32π)D.y ＝sin(2x －32π)5. 函数y ＝cos(432ππ+x )的最小正周期是__________. 6.要得到函数y ＝cos(2x －4π)的图象，只需将函数y ＝sin2x 的图象A.向左平移8π个单位B.向右平移8π个单位 C.向左平移4π个单位 D.向右平移4π个单位7.把函数y ＝cos(3x ＋4π)的图象适当变动就可以得到y ＝sin(－3x )的图象，这种变动可以是( ) A.向右平移4π B.向左平移4π C.向右平移12π D.向左平移12π8.如图b 是函数y ＝A sin(ωx ＋φ）＋2的图象的一部分，它的振幅、周期、初相各是( )A.A ＝3，Ｔ＝34π，φ＝－6πB.A ＝1，Ｔ＝34π，φ＝－43πC.A ＝1，Ｔ＝32π，φ＝－43πD.A ＝1，Ｔ＝34π，φ＝－6π9.如图c 是函数y ＝A sin （ωx ＋φ）的图象的一段，它的解析式为( )A.)32sin(32π+=x yB.)42sin(32π+=x yC.)3sin(32π-=x yD.)322sin(32π+=x y10.函数y ＝A sin （ωx ＋φ）（A ＞0，ω＞0）在同一周期内，当x ＝3π时，有y ｍa x ＝2，当x ＝0时，有y min ＝－2，则函数表达式是 .11.如图d 是f （x ）＝A sin （ωx ＋φ），A ＞0，｜φ｜＜2π的一段图象，则函数f （x ）的表达式为 .12.如图e ，是f （x ）＝A sin （ωx ＋φ），A ＞0，｜φ｜＜2π的一段图象，则f （x ）的表达式为 .13.如图f 所示的曲线是y ＝A sin （ωx ＋φ）（A ＞0，ω＞0）的图象的一部分，求这个函数的解析式.图c图d图e图f14.函数y ＝A sin （ωx ＋φ）＋ｋ（A ＞0，ω＞0）在同一周期内，当x ＝35π时，y 有最大值为37π，当x ＝311π时，y 有最小值－32，求此函数的解析式.15．由图g 所示函数图象，求y ＝A sin （ωx ＋φ）（｜φ｜＜π）的表达式.16．函数y ＝Asin(ωx ＋φ）（｜φ｜＜π）的图象如图h ，求函数的表达式.图g图h。