【精品】公式——广义胡克定律

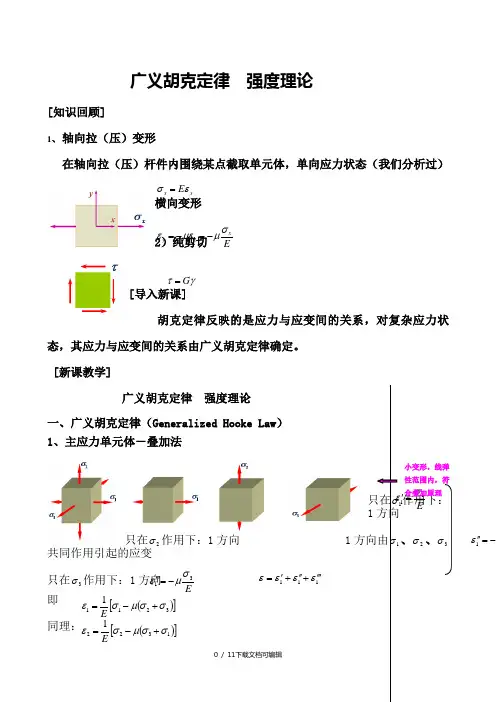
广义胡克定律 强度理论[知识回顾]1、 轴向拉（压）变形在轴向拉（压）杆件内围绕某点截取单元体，单向应力状态（我们分析过）横向变形2）纯剪切[导入新课]胡克定律反映的是应力与应变间的关系，对复杂应力状态，其应力与应变间的关系由广义胡克定律确定。

[新课教学]广义胡克定律 强度理论一、广义胡克定律（Generalized Hooke Law ） 1、主应力单元体－叠加法只在σ作用下：1方向只在2σ作用下：1方向 1方向由σ、2σ、3σ共同作用引起的应变只在3σ作用下：1方向 即同理： E11σ='1ε-=''E31σμε-='''111εεεε'''+''+'=()[]32111σσμσε+-=E()[]13221σσμσε+-=Exx E εσ=Exx y σμμεε-=-=γτG =小变形，线弹性范围内，符合叠加原理2、非主应力单元体 可以证明：对于各向同性材料，在小变形及线弹性范围内，线应变只与正应力有关，而与剪应力无关； 剪应变只与剪应力有关，而与正应力无关，满足应用叠加原理的条件。

3、体积应变 单元体，边长分别为dx 、dy 和dz 。

在三个互相垂直的面上有主应力1σ、2σ和3σ。

变形前单元体的体积为变形后，三个棱边的长度变为由于是单元体，变形后三个棱边仍互相垂直，所以，变形后的体积为dxdydz V )1)(1)(1(3211εεε+++=将上式展开，略去含二阶以上微量的各项，得 dxdydz V )1(3211εεε+++= 于是，单元体单位体积的改变为 3211εεεθ++=-=VVV θ称为体积应变（或体应变）。

它描述了构件内一点的体积变化程度。

5、体积应变与应力的关系将广义虎克定律（8-22）代入上式，得到以应力表示的体积应变()[]21331σσμσε+-=E[][][]⎪⎪⎪⎭⎪⎪⎪⎬⎫+-=+-=+-=)(1)(1)(1y x z z x z y y z y x x E E E σσμσεσσμσεσσμσε⎪⎪⎪⎭⎪⎪⎪⎬⎫===zx zx yz yz xy xy G G G τγτγτγ111dxdydzV =dz dz dz dydy dy dx dx dx )1()1()1(332211εεεεεε+=++=++=+K E m σσσσμθ=++⋅-==3)21(3321)(21321321σσσμεεεθ++-=++=E式中K 称为体积弹性模量，m σ是三个主应力的平均值。

胡克定律描述了弹性体在受到外力作用时发生的形变与施加力之间的关系。

在弹性限度内，胡克定律可以用以下公式表达：
F = kx
其中：
- F 表示施加在弹性体上的力（单位为牛顿，N）；
-k 是劲度系数，也称为弹性系数或胡克常数，它是一个表征材料弹性特性的常数（单位为牛顿每米，N/m）；
-x 是弹性体由于受力而产生的形变量，即伸长或压缩的长度（单位为米，m）。

劲度系数k 反映了材料的硬度或柔软度：一个较大的劲度系数意味着材料较硬，形变较难；一个较小的劲度系数则意味着材料较软，形变较容易。

胡克定律仅适用于弹性变形，即当物体在去除外力后能够恢复到原始形状的情况。

一旦超出弹性极限，物体可能会产生塑性变形，胡克定律就不再适用。

公式——广义胡克定律广义胡克定律是描述弹性体变形与所受力之间关系的一种数学公式。

它是由英国科学家罗伯特·胡克提出的，被广泛应用于弹簧、金属材料等弹性体的力学研究中。

广义胡克定律描述了物体中的应力（stress）与应变（strain）之间的关系，体现了物体恢复原状的能力。

广义胡克定律可以表示为：σ=Eε其中，σ是物体中的应力，E是材料的弹性模量，ε是应变。

应变也可以分为两种类型：正应变（tensile strain）和剪应变（shear strain）。

正应变是指物体长度或体积在受力后发生的相对变化，剪应变是指物体截面内的相对平移。

弹性模量E是物质的固有属性，反映了其变形能力。

E取决于材料的类型和结构。

对于大部分金属材料而言，它们在弹性变形区间表现出线性弹性行为，即广义胡克定律适用。

广义胡克定律适用于小应变情况，因为大应变时材料可能发生位移、塑性变形等非线性行为。

通常，当应变小于0.01时，广义胡克定律可以良好适用。

广义胡克定律的意义在于帮助我们理解物质在受力下产生的变形。

通过应用广义胡克定律，可以计算出物体所受力引起的应力，并据此评估物体是否会发生破裂、变形等情况。

例如，在弹簧的设计中，我们可以利用广义胡克定律来计算所需的弹簧刚度，以确保弹簧在受力下能够有效恢复原状。

需要注意的是，广义胡克定律只适用于线弹性材料，在材料的弹性极限之前。

对于塑性变形等非线性行为，需要使用其他力学模型进行描述。

总之，广义胡克定律是描述弹性体变形与所受力之间关系的重要公式。

在实际工程中，广义胡克定律的应用广泛，对于预测物体的变形和断裂行为，以及设计合适的材料和结构具有重要意义。

广义胡克定律 强度理论[知识回顾]1、 轴向拉（压）变形在轴向拉（压）杆件内围绕某点截取单元体，单向应力状态（我们分析过）横向变形2）纯剪切[导入新课]胡克定律反映的是应力与应变间的关系，对复杂应力状态，其应力与应变间的关系由广义胡克定律确定。

[新课教学]x x E εσ=E xx y σμμεε-=-=γτG =广义胡克定律 强度理论一、广义胡克定律（Generalized Hooke Law ）1、主应力单元体－叠加法只在1σ作用下：1方向只在2σ作用下：1方向 1方向由1σ、2σ、3σ共同作用引起的应变只在3σ作用下：1方向即同理：2、非主应力单元体可以证明：对于各向同性材料，在小变形及线弹性范围内，线应变只与正应力有关，而与剪应力无关； 剪应变只与剪应力有关，而与正应力无关， 满足应用叠加原理的条件。

E11σε='E21σμε-=''E 31σμε-='''111εεεε'''+''+'=()[]32111σσμσε+-=E()[]13221σσμσε+-=E()[]21331σσμσε+-=E [][][]⎪⎪⎪⎭⎪⎪⎪⎬⎫+-=+-=+-=)(1)(1)(1y x z z x z y y z y x x E E E σσμσεσσμσεσσμσε⎪⎪⎪⎭⎪⎪⎪⎬⎫===zx zx yz yz xy xy G G G τγτγτγ111小变形，线弹性范围内，符合叠加原理3、体积应变单元体，边长分别为dx 、dy 和dz 。

在三个互相垂直的面上有主应力1σ、2σ和3σ。

变形前单元体的体积为 变形后，三个棱边的长度变为由于是单元体，变形后三个棱边仍互相垂直，所以，变形后的体积为dxdydz V )1)(1)(1(3211εεε+++=将上式展开，略去含二阶以上微量的各项，得dxdydz V )1(3211εεε+++= 于是，单元体单位体积的改变为 3211εεεθ++=-=VVV θ称为体积应变（或体应变）。

第四章 广义胡克定律第四章 广义胡克定律 (1)§4.1节广义胡克定律 (2)§4.2节拉梅常数与工程弹性常数 (5)§4.3节弹性应变能函数 (7)§4.1节 广义胡克定律（一）单向应力状态下胡克定律单向应力状态下，处于线弹性阶段材料，其应力与应变关系可由下式表示：x x E σε=其中E 为材料的弹性模量。

（二）三维广义胡克定律三维条件下，物体应力状态可由6个分量表示，而应变状态也由6个分量表示。

假设应力与应变的各个分量之间均相关，一般地，1111111222133314121523163122211122222333241225232631333111322233333412352336311241114222433344124523463123511152225c c c c c c c c c c c c c c c c c c c c c c c c c c c σεεεεεεσεεεεεεσεεεεεεσεεεεεεσεε=+++++=+++++=+++++=+++++=++33354125523563131611162226333641265236631c c c c c c c c c εεεεσεεεεεε⎧⎪⎪⎪⎪⎨⎪⎪+++⎪=+++++⎪⎩ 或写作111213141516111121222324252622223132333435363333121241424344454623235152535455563131616263646566c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c c σεσεσεσεσεσε⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎢⎥⎢⎥⎢⎣⎦⎣⎦⎣⎦⎥⎥⎥⎥⎥ 其中，mn C （,1,,6m n ="）为弹性常数。

胡克定律,弹力与物体的变形成正比,而与物体的质量成反比胡克定律是物理学中的一个基本定律，它描述了弹性物体在受到外力作用时，其形变与外力之间的关系。

这个定律是由英国物理学家罗伯特·胡克在17世纪提出的，它对于理解弹性物体的力学行为具有重要意义。

胡克定律的内容是：在弹性限度内，弹簧的伸长或压缩量与作用在其上的外力成正比，而与物体的质量无关。

也就是说，当一个物体受到的力越大，它所发生的形变也就越大。

这个定律可以用一个简单的数学公式来表示：F=k×Δx其中，F代表作用在物体上的力，k是弹簧的劲度系数，Δx是弹簧的伸长或压缩量。

这个公式告诉我们，当外力增加时，弹簧的形变也会增加，而且这种增加是线性的，也就是说，形变和外力之间存在着一种正比关系。

这个正比关系意味着，当一个物体受到的力越大，它所发生的形变也就越大。

这是因为物体在受到外力作用时，其内部的分子或原子之间的相互作用力会发生变化，导致物体形状的改变。

而这种改变的大小与外力的大小成正比。

另外，胡克定律还告诉我们，弹簧的劲度系数k是一个常数，它与物体的质量无关。

这意味着无论物体的质量大小如何，只要它受到的力相同，它所发生的形变也是相同的。

这是因为物体的质量不会影响其内部的分子或原子之间的相互作用力，因此也不会影响其形变的大小。

这个结论在工程学和物理学中具有重要意义。

在工程设计中，工程师们经常需要使用弹性材料来制造各种机械和结构。

胡克定律可以帮助他们了解弹性材料在不同外力作用下的形变情况，从而优化设计，提高产品的稳定性和安全性。

在物理学中，胡克定律也是研究弹性物体力学行为的基础。

通过研究不同弹性材料在不同外力作用下的形变情况，物理学家们可以进一步探索弹性材料的内部结构和性质，为材料科学和工程学的发展提供重要的理论支持。

总之，胡克定律是物理学中的一个基本定律，它描述了弹性物体在受到外力作用时其形变与外力之间的关系。

这个定律告诉我们，当一个物体受到的力越大，它所发生的形变也就越大；而弹簧的劲度系数k是一个常数，它与物体的质量无关。

胡克定律，曾译为虎克定律，是力学弹性理论中的一条基本定律，表述为：固体材料受力之后，材料中的应力与应变（单位变形量）之间成线性关係。

满足胡克定律的材料称为线弹性或胡克型（英文Hookean）材料。

从物理的角度看，胡克定律源于多数固体（或孤立分子）内部的原子在无外载作用下处于稳定平衡的状态。

许多实际材料，如一根长度为L、横截面积A的稜柱形棒，在力学上都可以用胡克定律来模拟——其单位伸长（或缩减）量（应变）在常係数E（称为弹性模量）下，与拉（或压）应力σ成正比例，即：F=-k·x或△F=-k·Δx
其中为总伸长（或缩减）量。

胡克定律用17世纪英国物理学家罗伯特·胡克的名字命名。

胡克提出该定律的过程颇有趣味，他于1676年发表了一句拉丁语字谜，谜面是：ceiiinosssttuv。

两年后他公布了谜底是：ut tensio sic vis，意思是“力如伸长（那样变化）”（见参考文献[1]），这正是胡克定律的中心内容。

胡克定律、胡克定律： F = Kx (x为伸长量或压缩量,K为倔强系数，只与弹簧的原长、粗细和材料有关)2、重⼒：G = mg (g随⾼度、纬度⽽变化)⼒矩：M=FL (L为⼒臂，是转动轴到⼒的作⽤线的垂直距离）5、摩擦⼒的公式：(1 ) 滑动摩擦⼒：f=µN说明：a、N为接触⾯间的弹⼒，可以⼤于G；也可以等于G;也可以⼩于G 为滑动摩擦系数，只与接触⾯材料和粗糙程度有关，与接触⾯µb、积⼤⼩、接触⾯相对运动快慢以及正压⼒N⽆关.(2 ) 静摩擦⼒：由物体的平衡条件或⽜顿第⼆定律求解,与正压⼒⽆关.fm (fm为最⼤静摩擦⼒，与正压⼒有关)≤ f静≤⼤⼩范围：O说明：a 、摩擦⼒可以与运动⽅向相同，也可以与运动⽅向相反，还可以与运动⽅向成⼀定夹⾓。

b、摩擦⼒可以作正功，也可以作负功，还可以不作功。

c、摩擦⼒的⽅向与物体间相对运动的⽅向或相对运动趋势的⽅向相反。

d、静⽌的物体可以受滑动摩擦⼒的作⽤，运动的物体可以受静摩擦⼒的作⽤。

Vg (注意单位）ρ6、浮⼒：F=7、万有引⼒：F=GmM/r2(1)．适⽤条件(2) ．G为万有引⼒恒量(3) ．在天体上的应⽤：（M⼀天体质量R⼀天体半径g⼀天体表⾯重⼒加速度）a 、万有引⼒=向⼼⼒Gb、在地球表⾯附近，重⼒=万有引⼒mg=GmM/r2c、第⼀宇宙速度mg = m V=8、库仑⼒：F=K (适⽤条件)9、电场⼒：F=qE (F 与电场强度的⽅向可以相同，也可以相反)10、磁场⼒：（1）洛仑兹⼒：磁场对运动电荷的作⽤⼒。

V) ⽅向⼀左⼿定⊥公式：f=BqV (B（2）安培⼒：磁场对电流的作⽤⼒。

I）⽅向⼀左⼿定则⊥公式：F= BIL （BFy = m ay∑Fx = m ax ∑11、⽜顿第⼆定律：F合= ma 或者理解：（1）⽮量性（2）瞬时性（3）独⽴性（4）同⼀性12、匀变速直线运动：基本规律：Vt = V0 + a t S = vo t + a t2⼏个重要推论：(1) Vt2 －V02 = 2as （匀加速直线运动：a为正值匀减速直线运动：a为正值）(2) A B段中间时刻的即时速度:Vt/ 2 = = A S a t B(3) AB段位移中点的即时速度:Vs/2 =匀速：Vt/2 =Vs/2 ; 匀加速或匀减速直线运动：Vt/2(4) 初速为零的匀加速直线运动,在1s 、2s、3s?……ns内的位移之⽐为12：22:32……n2；在第1s 内、第2s内、第3s内……第ns内的位移之⽐为1：3：5…… (2n-1); 在第1⽶内、第2⽶内、第3⽶内……第n⽶内的时间之⽐为1：：……((5) 初速⽆论是否为零,匀变速直线运动的质点,在连续相邻的相等的时间间隔内的位s = aT2 (a⼀匀变速直线运动的加速度T⼀每个时间间隔的时间)?移之差为⼀常数：13、竖直上抛运动：上升过程是匀减速直线运动，下落过程是匀加速直线运动。