三向应力状态的广义胡克定律
- 格式:ppt
- 大小:2.32 MB
- 文档页数:4



广义胡克定律公式推导
广义胡克定律是描述材料弹性行为的重要定律,其公式为 F - k·x 或 F - k·x,其中 F 是施加的外部力,k 是物体的劲度系数,x 是形变量。
在三维情况下,广义胡克定律是三个方程,可以将这三个方程的应力应变提出来写成矩阵形式。
首先,将三维情况下的广义胡克定律写成矢量形式,即 F = k·e,其中 e 是应变矢量,定义为形变前后物体的长度差。
接着,将矢量 F 与应变矢量 e 之间的关系表示为矩阵形式,即 F = k·E,其中 E 是胡克应变矩阵,定义为胡克应变矩阵胡克应变矩阵。
最后,将胡克应变矩阵表示成矢量胡克应变矩阵,即 E = [e_x e_y e_z],然后将其代入矩阵形式的广义胡克定律中,得到三维情况下的广义胡克定律矩阵形式为:
[F_x - k·e_x] = [0 0 0]
[F_y - k·e_y] = [0 0 0]
[F_z - k·e_z] = [0 0 0]
其中,F_x、F_y、F_z 分别表示外部力在 x、y、z 方向上的投影,e_x、e_y、e_z 分别表示对应的应变矢量。
可以看出,三维情况下的广义胡克定律矩阵形式正是反映了物体在三维空间中的弹性行为。

三向的胡克定律一、三向胡克定律的基础概念三向胡克定律,又称为三维胡克定律,是弹性力学的基本定律之一。
它描述了在三维空间中,物体的应力和应变之间的关系。
与传统的二维胡克定律相比,三向胡克定律考虑了更多的因素,包括剪切应力、旋转应力和三维空间的应变状态。
在三向胡克定律中,物体的应力和应变被表示为三维向量,这些向量不仅包括大小,还包括方向。
这使得三向胡克定律能够更准确地描述在复杂应力状态下的物体行为,如扭曲、弯曲和剪切等。
二、三向胡克定律的数学表达三向胡克定律的数学表达通常由三个方程构成:应力平衡方程、几何方程和物理方程。
这些方程一起描述了物体的应力、应变和变形之间的关系。
1.应力平衡方程:该方程描述了物体内部应力的平衡状态。
在三维空间中,这个方程是一个线性方程组,表示为:σij,j=0 (i=1,2,3)。
其中,σij表示应力张量分量,j表示偏量算子。
2.几何方程:这个方程描述了物体的应变和变形。
它通常表示为:εij=1/2(uij+uji),其中εij表示应变张量分量,uij表示位移梯度分量。
3.物理方程:这个方程将应力和应变联系起来,通常表示为:σij=λδij+2μεij。
其中,λ和μ是拉梅常数,δij是克罗内克符号,表示当i=j时值为1,否则为0。
三、三向胡克定律的应用三向胡克定律在许多工程领域中有广泛的应用,包括结构工程、航空航天工程和材料科学等。
以下是一些具体的应用实例:1.结构工程:在结构工程中,三向胡克定律被用于分析桥梁、建筑和其它大型结构的应力分布和变形。
这种分析可以帮助工程师预测结构的强度、刚度和稳定性,从而优化设计。
2.航空航天工程:在航空航天工程中,由于飞行器经常处于复杂的应力状态,因此三向胡克定律的应用尤为重要。
它被用于分析飞行器的结构强度、疲劳寿命和气动弹性等问题。
3.材料科学:在材料科学中,三向胡克定律用于研究材料的力学性能,如弹性模量、泊松比和剪切模量等。
这种研究有助于理解材料的微观结构和宏观力学行为之间的关系,为新材料的开发提供理论支持。

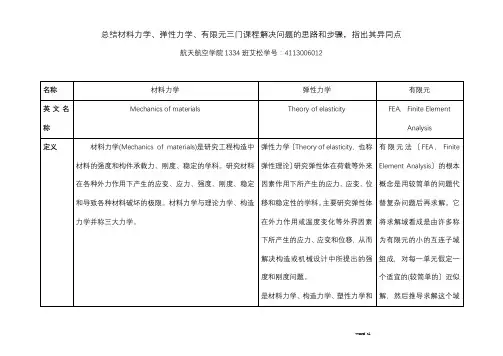
总结材料力学、弹性力学、有限元三门课程解决问题的思路和步骤,指出其异同点航天航空学院1334班艾松学号:4113006012线性关系,这类问题称为几何非线性问题。
③物理非线性问题。
在这类问题中,材料内的变形和内力之间〔如应变和应力之间〕不满足线性关系,即材料不服从胡克定律。
在几何非线性问题和物理非线性问题中,叠加原理失效。
解决这类问题可利用卡氏第一定理、克罗蒂-恩盖塞定理或采用单位载荷法等。
在许多工程构造中,杆件往往在复杂载荷的作用或复杂环境的影响下发生破坏。
例如,杆件在交变载荷作用下发生疲劳破坏,在高温恒载条件下因蠕变而破坏,或受高速动载荷的冲击而破坏等。
这些破坏是使机械和工程构造丧失工作能力的主要原因。
所以,材料力学还研究材料的疲劳性能、蠕变性能和冲击性能。
材料力学根本公式〔解决问题方法〕: 一、应力与强度条件 拉压:[]σσ≤=maxmax AN平衡微分方程〔1〕几何方程〔2〕物理方程〔3〕成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式,借助于变分原理或加权余量法,将微分方程离散求解。
采用不同的权函数和插值函数形式,便构成不同的有限元方法。
有限元方法最早应用于构造力学,后来随着计算机的开展慢慢用于流体力学的数值模拟。
在有限元方法中,把计算域离散剖分为有限个互不重叠且相互连接的单元,在每个剪切:[]ττ≤=AQ max挤压:[]挤压挤压挤压σσ≤=AP圆轴扭转:[]ττ≤=W tTmax 平面弯曲: ①[]σσ≤=maxzmax W M②[]max t max t maxmax σσ≤=y I M z t max c max maxy I Mzc =σ[]cnax σ≤ ③[]ττ≤⋅=bI S Q z *max z max max斜弯曲:[]σσ≤+=maxyyz z max W M W M拉〔压〕弯组合:[]σσ≤+=maxmax zW MA N[]t max t z max t σσ≤+=y I M A N z []c max c z z max c σσ≤-=ANy I M 圆轴弯扭组合: ① 第三强度理论[]στσσ≤+=+=z2n2w2n 2w r34W M M(1)式中的σx 、σy 、σz 、τyz=τzy 、τxz=τzx 、τxy=τyx 为应力分量,X 、Y 、Z 为单位体积的体力在三个坐标方向的分量;(2)式中的u 、v 、w 为位移矢量的三个分量〔简称位移分量〕,εx 、εy 、εz 、γyz 、γxz 、γxy 为应变分量;(3)式中的E 和v 分别表示杨氏弹性模量和泊松比。

1.外力偶矩计算公式〔P功率,n转速〕2.弯矩、剪力和荷载集度之间的关系式3.轴向拉压杆横截面上正应力的计算公式〔杆件横截面轴力F N,横截面面积A,拉应力为正〕4.轴向拉压杆斜截面上的正应力与切应力计算公式〔夹角a 从x轴正方向逆时针转至外法线的方位角为正〕5.纵向变形和横向变形〔拉伸前试样标距l,拉伸后试样标距l1;拉伸前试样直径d,拉伸后试样直径d1〕6.纵向线应变和横向线应变7.泊松比8.胡克定律9.受多个力作用的杆件纵向变形计算公式?10.承受轴向分布力或变截面的杆件,纵向变形计算公式11.轴向拉压杆的强度计算公式12.许用应力,脆性材料,塑性材料13.延伸率14.截面收缩率15.剪切胡克定律〔切变模量G,切应变g 〕16.拉压弹性模量E、泊松比和切变模量G之间关系式17.圆截面对圆心的极惯性矩〔a〕实心圆〔b〕空心圆18.圆轴改变时横截面上任一点切应力计算公式〔扭矩T,所求点到圆心间隔r〕19.圆截面周边各点处最大切应力计算公式20.改变截面系数,〔a〕实心圆〔b〕空心圆21.薄壁圆管〔壁厚δ≤ R0 /10 ,R0为圆管的平均半径〕改变切应力计算公式22.圆轴改变角与扭矩T、杆长l、改变刚度GH p的关系式23.同一材料制成的圆轴各段内的扭矩不同或各段的直径不同〔如阶梯轴〕时或24.等直圆轴强度条件25.塑性材料;脆性材料26.改变圆轴的刚度条件? 或27.受内压圆筒形薄壁容器横截面和纵截面上的应力计算公式,28.平面应力状态下斜截面应力的一般公式,29.平面应力状态的三个主应力,,30.主平面方位的计算公式31.面内最大切应力32.受扭圆轴外表某点的三个主应力,,33.三向应力状态最大与最小正应力 ,34.三向应力状态最大切应力35.广义胡克定律36.四种强度理论的相当应力37.一种常见的应力状态的强度条件,38.组合图形的形心坐标计算公式,39.任意截面图形对一点的极惯性矩与以该点为原点的任意两正交坐标轴的惯性矩之和的关系式40.截面图形对轴z和轴y的惯性半径? ,41.平行移轴公式〔形心轴z c与平行轴z1的间隔为a,图形面积为A〕42.纯弯曲梁的正应力计算公式43.横力弯曲最大正应力计算公式44.矩形、圆形、空心圆形的弯曲截面系数? ,,45.几种常见截面的最大弯曲切应力计算公式〔为中性轴一侧的横截面对中性轴z的静矩,b为横截面在中性轴处的宽度〕46.矩形截面梁最大弯曲切应力发生在中性轴处47.工字形截面梁腹板上的弯曲切应力近似公式48.轧制工字钢梁最大弯曲切应力计算公式49.圆形截面梁最大弯曲切应力发生在中性轴处50.圆环形薄壁截面梁最大弯曲切应力发生在中性轴处51.弯曲正应力强度条件52.几种常见截面梁的弯曲切应力强度条件53.弯曲梁危险点上既有正应力σ又有切应力τ作用时的强度条件或,54.梁的挠曲线近似微分方程55.梁的转角方程56.梁的挠曲线方程?57.轴向荷载与横向均布荷载结合作用时杆件截面底部边缘和顶部边缘处的正应力计算公式58.偏心拉伸〔压缩〕59.弯扭组合变形时圆截面杆按第三和第四强度理论建立的强度条件表达式,60.圆截面杆横截面上有两个弯矩和同时作用时,合成弯矩为61.圆截面杆横截面上有两个弯矩和同时作用时强度计算公式62.63.弯拉扭或弯压扭组合作用时强度计算公式64.剪实在用计算的强度条件65.挤压实用计算的强度条件66.等截面细长压杆在四种杆端约束情况下的临界力计算公式67.68.压杆的长细比或柔度计算公式,69.细长压杆临界应力的欧拉公式70.欧拉公式的适用范围71.压杆稳定性计算的平安系数法72.压杆稳定性计算的折减系数法73.关系需查表求得3 截面的几何参数4 应力和应变5 应力状态分析6 内力和内力图7 强度计算8 刚度校核9 压杆稳定性校核10 动荷载11 能量法和简单超静定问题材料力学公式汇总一、应力与强度条件 1、 拉压 []σσ≤=maxmax AN2、 剪切 []ττ≤=AQmax 挤压 []挤压挤压挤压σσ≤=AP3、 圆轴改变 []ττ≤=W tTmax 4、平面弯曲 ①[]σσ≤=maxz max W M②[]max t max t max max σσ≤=y I M ztmax c max max y I Mzc =σ[]cnax σ≤③[]ττ≤⋅=bI S Q z *max z max max5、斜弯曲 []σσ≤+=maxyyz z max W M W M6、拉〔压〕弯组合 []σσ≤+=maxmax zW M A N[]t max t zmax t σσ≤+=y I M A N z[]c max c z z max c σσ≤-=A N y I M 注意:“5〞与“6〞两式仅供参考 7、圆轴弯扭组合:①第三强度理论 []στσσ≤+=+=z2n2w 2n2wr34W M M②第四强度理论[]στσσ≤+=+=z2n2w 2n2wr475.03W M M二、变形及刚度条件1、 拉压 ∑⎰===∆LEAxx N EALN EANL L d )(ii2、 改变 ()⎰=∑==Φpp i i p GI dxx T GI LT GI TL πφ0180⋅=Φ=p GI T L 〔m / 〕3、 弯曲(1)积分法:)()(''x M x EIy = C x x M x EI x EIy +==⎰d )()()('θ D Cx x x x M x EIy ++=⎰⎰d ]d )([)((2)叠加法:()21,P P f …=()()21P f P f ++…, ()21,P P θ=()()++21P P θθ…(3)根本变形表(注意:以下各公式均指绝对值,使用时要根据详细情况赋予正负号)EI ML B =θ EI PL B 22=θ EIqL B 63=θEIML f B 22=EI PL f B 33= EI qL f B 84=EI ML B 3=θ,EI ML A 6=θ EI PL A B 162==θθ EIqL A B 243==θθEI ML f c 162=EI PL f c 483= EIqL f c 3844= (4)弹性变形能(注:以下只给出弯曲构件的变形能,并忽略剪力影响,其他变形与此相似,不予写出)EIL M U 22==ii i EI L M 22∑=()⎰EIdx x M 22 (5)卡氏第二定理(注:只给出线性弹性弯曲梁的公式)=∂∂=∆i i P U()()⎰∂∂∑dx P x M EI x M i三、应力状态与强度理论 1、 二向应力状态斜截面应力ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=2、 二向应力状态极值正应力及所在截面方位角22min max )2(2xyy x y x τσσσσσσ+-±+=yx xyσστα--=22tg 0PAB MAB A BqL LLLL3、 二向应力状态的极值剪应力22max )2(xyyx τσστ+-=注:极值正应力所在截面与极值剪应力所在截面夹角为450 4、 三向应力状态的主应力:321σσσ≥≥最大剪应力:231max σστ-=5、二向应力状态的广义胡克定律〔1〕、表达形式之一〔用应力表示应变〕)(1y x x Eμσσε-= )(1x y y Eμσσε-= )(y x z Eσσμε+-= Gxy xy τγ=〔2〕、表达形式之二〔用应变表示应力〕)(12y x x E μεεμσ+-= )(12x y y Eμεεμσ+-= 0=z σ xy xy G γτ=6、三向应力状态的广义胡克定律()[]z y x x Eσσμσε+-=1()z y x ,,Gxyxy τγ=()zx yz xy ,,7、强度理论 〔1〕[]111σσσ≤=r ()3212σσμσσ+-=r []σ≤[]bb n σσ=〔2〕[]σσσσ≤-=313r()()()[]213232221421σσσσσσσ-+-+-=r []σ≤ []ss n σσ=8、平面应力状态下的应变分析 〔1〕αγαεεεεεα2sin 22cos 22⎪⎪⎭⎫⎝⎛---++=xyyx y x+-=⎪⎭⎫ ⎝⎛-αεεγα2sin 22yx αγ2cos 2⎪⎪⎭⎫ ⎝⎛-xy 〔2〕22min max 222⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-±+=xy y x yx γεεεεεεyx xyεεγα-=02tg四、压杆稳定1、临界压力与临界应力公式〔假设把直杆分为三类〕①细长受压杆 p λλ≥ ()2min 2cr L EI P μπ= 22cr λπσE=②中长受压杆 s p λλλ≥≥ λσb a -=cr③短粗受压杆s λλ≤ “cr σ〞=s σ或 b σ2、关于柔度的几个公式 i Lμλ= p2p σπλE=ba s s σλ-=3、惯性半径公式AI i z= 〔圆截面4di z =,矩形截面12min b i =〔b 为短边长度〕〕五、动载荷〔只给出冲击问题的有关公式〕 能量方程 U V T ∆=∆+∆冲击系数 std 211∆++=hK 〔自由落体冲击〕st20d ∆=g v K 〔程度冲击〕六、截面几何性质1、 惯性矩〔以下只给出公式,不注明截面的形状〕⎰=dA I P 2ρ=324d π ()44132απ-D Dd =α ⎰==6442d dA y I z π ()44164απ-D 123bh123hb 323maxd y I W zz π==()43132απ-D62bh62hb2、惯性矩平移轴公式A a I I 2zc z +=。
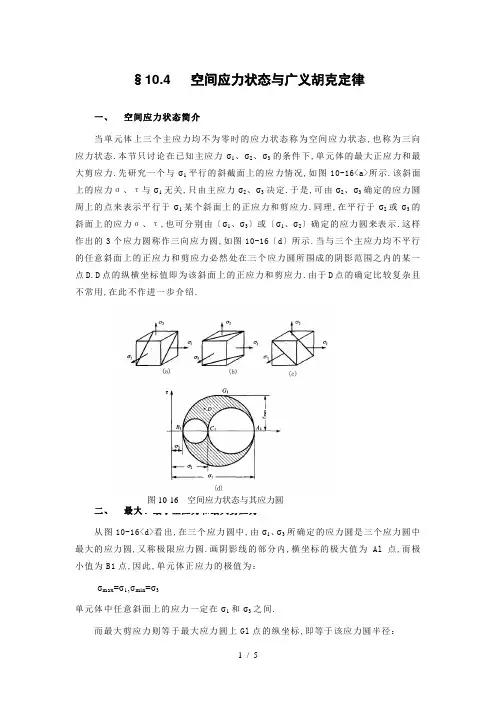
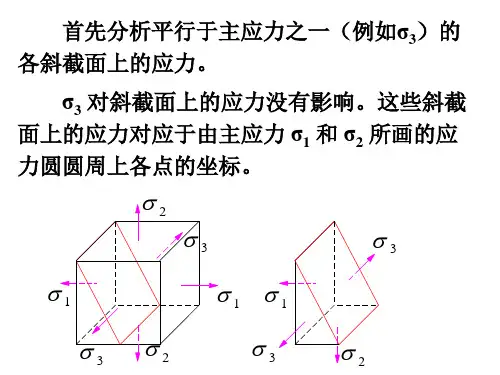
§10.4 空间应力状态与广义胡克定律一、空间应力状态简介当单元体上三个主应力均不为零时的应力状态称为空间应力状态,也称为三向应力状态.本节只讨论在已知主应力σ1、σ2、σ3的条件下,单元体的最大正应力和最大剪应力.先研究一个与σ1平行的斜截面上的应力情况,如图10-16<a>所示.该斜面上的应力σ、τ与σ1无关,只由主应力σ2、σ3决定.于是,可由σ2、σ3确定的应力圆周上的点来表示平行于σ1某个斜面上的正应力和剪应力.同理,在平行于σ2或σ3的斜面上的应力σ、τ,也可分别由〔σ1、σ3〕或〔σ1、σ2〕确定的应力圆来表示.这样作出的3个应力圆称作三向应力圆,如图10-16〔d〕所示.当与三个主应力均不平行的任意斜面上的正应力和剪应力必然处在三个应力圆所围成的阴影范围之内的某一点D.D点的纵横坐标值即为该斜面上的正应力和剪应力.由于D点的确定比较复杂且不常用,在此不作进一步介绍.图10-16 空间应力状态与其应力圆二、最大、最小正应力和最大剪应力从图10-16<d>看出,在三个应力圆中,由σ1、σ3所确定的应力圆是三个应力圆中最大的应力圆,又称极限应力圆.画阴影线的部分内,横坐标的极大值为Al点,而极小值为B1点,因此,单元体正应力的极值为:σmax=σ1,σmin=σ3单元体中任意斜面上的应力一定在σ1和σ3之间.而最大剪应力则等于最大应力圆上Gl点的纵坐标,即等于该应力圆半径:Gl 点在由σ1和σ3所确定的圆周上,此圆周上各点的纵横坐标就是与σ2轴平行的一组斜截面上的应力,所以单元体的最大剪应力所在的平面与σ2轴平行,且与σ1和σ3主平面交450.三、广义胡克定律在研究单向拉伸与压缩时,已经知道了在线弹性范围内,应力与应变成线性关系,满足胡克定律 E σε= 〔a 〕此外,轴向变形还将引起横向尺寸的变化,横向线应变根据材料的泊松比可得出:'E σεμεμ=-=- 〔b 〕在纯剪切的情况下,根据实验结果,在剪应力不超过剪切比例极限时,剪应力和剪应变之间的关系服从剪切胡克定律,即G τγ= 或 G τγ= 〔c 〕对于复杂受力情况,描述物体一点的应力状态,通常需要9个应力分量,如图10.1所示.根据剪应力互等定律,τxy =-τyx ,τxz =-τzx ,τyz =-τzy ,因而,在这9个应力分量中只有6个是独立的.这种情况可以看成是三组单向应力〔图10-17〕和三组纯剪切的组合.对于各向同性材料,在线弹性范围内,处于小变形时,线应变只与正应力有关,与剪应力无关;而剪应变只与剪应力有关,与正应力无关,并且剪应力只能引起与其相对应的剪应变分量的改变,而不会影响其它方向上的剪应变.因此,求线应变时,可不考虑剪应力的影响,求剪应变时不考虑正应力的影响.于是只要利用〔a 〕、〔b 〕、〔c 〕三式求出与各个应力分量对应的应变分量,然后进行叠加即可.图10-17 应力分解如在正应力σx 单独作用时<图10-17<b>>,单元体在x 方向的线应变xxx E σε=;在σy 单独作用时<图10-17<c>>,单元体在x 方向的线应变为:yxy E σεμ=-;在σz 单独作用时<图10-17 <d>>,单元体在x 方向的线应变为zxz E σεμ=-;在σx 、σy 、σz 共同作用下,单元体在x 方向的线应变为:同理,可求出单元体在y 和z 方向的线应变εy 和εz.最后得 1()y y z x E εσμσσ=-+⎡⎤⎣⎦ 〔10-9〕对于剪应变与剪应力之间,由于剪应变只与剪应力有关,并且剪应力只能引起与其相对应的剪应变分量的改变,而不会影响其它方向上的剪应变.因而仍然是〔c 〕式所表示的关系.这样,在xy 、yz 、zx 三个面内的剪应变分别是12(1)yz yz yz G E μγττ+== 〔10-10〕公式〔10-9〕和〔10-10〕就是三向应力状态时的广义胡克定律.当单元体的六个面是主平面时,使x 、y 、z 的方向分别与主应力σ1、σ2、σ3的方向一致,这时有广义胡克定律化为:[]22311()E εσμσσ=-+ 〔10-11〕ε1、ε2、ε3方向分别与主应力σ1、σ2、σ3的方向一致,称为一点处的主应变.三个主应变按代数值的大小排列,ε1 ≥ ε2 ≥ε3,其中,ε1和ε3分别是该点处沿各方向线应变的最大值和最小值.四、 体积应变单位体积的改变称为体积应变〔体应变〕.图10-18所示的主单元体,边长分别是dx 、dy 和dz.在3个互相垂直的面上有主应力σ1、σ2和σ3.单元体变形前的体积为: v = dxdydz ;变形后的体积为:v 1=〔dx +ε1dx><dy +ε2dy><dz+ε3dz>则体积应变为:略去高阶微量,得 123θεεε=++ 〔10-12〕将广义胡克定律式<10-11>代入上式,得到以应力表示的体积应变图10-18 主应力单12312312()E μθεεεσσσ-=++=++ 〔10-13〕令 1231()3m σσσσ=++ 〔10-14〕则 3(12)m m E K μσσθ-== 〔10-15〕式中:3(12)E K μ=-称为体积弹性模量,σm 称为平均主应力.公式〔10-15〕表明,体积应变θ与平均主应力σm 成正比,即体积胡克定律.单位体积的体积改变只与三个主应力之和有关,至于三个主应力之间的比例对体积应变没有影响.若将图10-19〔a 〕中所示单元体分解为〔b 〕和〔c 〕两种情况的叠加,在〔c 〕图中,由于各面上的主应力为平均主应力,该单元体各边长按相同比例伸长或缩短,所以单元体只发生体积改变而不发生形状改变.在图〔b 〕中,三个主应力之和为零,由式〔10-13〕可得其体积应变θ也为零,表明该单元体只发生形状改变而不发生体积改变.由此可知,图〔a 〕所示的单元体的变形将同时包括体积改变和形状改变.五、 复杂应力状态下的弹性变形比能弹性变形比能是指物体在外力作用处于弹性状态下,在单位体积内储存的变形能.在单向应力状态下,当应力σ与应变ε满足线性关系时,根据外力功和应变能在数值上相等的关系,导出变形比能的计算公式为图10-19 单元体应力的组合在复杂应力状态下的单元体的变形比能为将将广义胡克定律<10.11>式代入上式,经过整理后得出:22212312233112()2E σσσμσσσσσσ⎡⎤=++-++⎣⎦ 〔10-16〕 式〔10-16〕就是在复杂应力状态下杆件的弹性变形比能计算公式.由于单元体的变形包括体积改变和形状改变,所以变形比能也可以看成由体积改变比能和形状改变比能这两部分的组合.式中:u θ为体积改变比能,d u 为形状改变比能.对于图〔10-19〔c 〕〕中的单元体,各面上的正应力为:1231()3m σσσσ==++,将σm 代入式〔10-16〕得体积改变比能: 212312()6E μσσσ-=++ 〔10-17〕形状改变比能:2221223311[()()()]6E μσσσσσσ+=-+-+- 〔10-18〕 例10-7 如图10-20所示钢梁,在梁的A 点处测得线应变640010,x ε-=⨯612010,y ε-=-⨯ 试求:A 点处沿x 、y 方向的正应力和z 方向的线应变.已知弹性模量E=200GPa,泊松比μ=0.3.图10-20 钢梁上某点A 的位置解:因为A 点的单元体上σz=0,该单元体处于平面应力状态,将εx 、εy 、E 、μ代入公式〔10-9〕,得解得:σx=80MPa,σy=0再由。
总结材料力学、弹性力学、有限元三门课程解决问题的思路和步骤,指出其异同点航天航空学院1334班艾松学号:4113006012杆件在多种外力共同作用下的变形(或力),可先分别求出各外力单独作用下杆件的变形(或力),然后将这些变形(或力)叠加,从而得到最终结果。
②几何非线性问题。
若杆件变形较大,就不能在原有几何形状的基础上分析力的平衡,而应在变形后的几何形状的基础上进行分析。
这样,力和变形之间就会出现非线性关系,这类问题称为几何非线性问题。
③物理非线性问题。
在这类问题中,材料的变形和力之间(如应变和应力之间)不满足线性关系,即材料不服从胡克定律。
在几何非线性问题和物理非线性问题中,叠加原理失效。
解决这类问题可利用卡氏第一定理、克罗蒂-恩盖塞定理或采用单位载荷法解。
直角坐标系下的弹性力学的基本方程为:平衡微分方程(1)几何方程(2)物理方程(3)(1)式中的σx、σy、σz、τyz=τzy、τxz=τzx、τxy=τyx为应力分量,X、Y、函数的插值点,将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式,借助于变分原理或加权余量法,将微分方程离散求解。
采用不同的权函数和插值函数形式,便构成不同的有限元方法。
有限元方法最早应用于结构力学,后来随着计算机的发展慢慢用于流体力学的数值模拟。
在有限元方法中,把计算域离散剖分为有限个互不重叠且相互连接的单元,在每个单元选择基函数,用单元基函数的线形组合来逼近单元中的真解,整个计算域上总体的基函数可以看为由每个单二、变形及刚度条件 拉压:∑⎰===∆LEAxx N EAL N EANLL d )(ii 扭转:()⎰=∑==Φpp i i p GI dx x T GI L T GI TLπφ0180⋅=Φ=p GI T L弯曲:(1)积分法:)()(''x M x EIy =C x x M x EI x EIy +==⎰d )()()('θD Cx x x x M x EIy ++=⎰⎰d ]d )([)((2)叠加法:()21,P P f …=()()21P f P f ++…()21,P P θ=()()++21P P θθ…三、应力状态与强度理论 二向应力状态斜截面应力:ατασσσσσα2sin 2cos 22xy yx yx --++=ατασστα2cos 2sin 2xy yx +-=二向应力状态极值正应力及所在截面方位角:到。