当前位置：文档之家 › 弹塑性力学第四章

弹塑性力学第四章

  • 格式：ppt
  • 大小：4.01 MB
  • 文档页数：73

下载文档原格式

  / 73

合集下载

弹塑性力学第四章答案

弹塑性力学第四章答案

第四章 习题答案4.3有一块宽为a ，高为b 的矩形薄板，其左边及下边受链杆支承，在右边及上边分别受均布压力1q 和2q 作用，见题图4.1，如不计体力，试求薄板的位移。

题图4-1解：1.设置位移函数为123123()()u x A A x A y v y B B x B y =+++⎫⎬=+++⎭（1）因为边界上没有不等于零的已知位移，所以式00,m m m m mmu u A u v v A v =+=+∑∑中的0u 、0v 都取为零，显然，不论式（1）中各系数取何值，它都满足左边及下边的位移边界条件，但不一定能满足应力边界条件，故只能采用瑞兹法求解。

2.计算形变势能。

为简便起见，只取1A 、1B 两个系数。

111111,u A x Au v B y B v ==== （2） 11,0,,0uuvu A B x yyx∂∂∂∂====∂∂∂∂ ()()2222111111112200222(1)2(1)a b E Eab U A B A B dxdy A B A B v v νν=++=++--⎰⎰ （3） 3.确定系数1A 和1B ，求出位移解答。

因为不计体力()0X Y ==，且注意到1m =，式4-14简化为11UXu ds A ∂=∂⎰ （4）11UYv ds B ∂=∂⎰ （5） 对式（4）右端积分时，在薄板的上下边和左边，不是0X =，就是10u =，故积分值为零。

在右边界上有11,,X q u x a ds dy =-===()111bXu ds q ady q ab =-=-⎰⎰ （6）同理，式（5）右端的积分只需在薄板的上边界进行，()1220aYv ds q bdx q ab =-=-⎰⎰ （7）将式（3）、式（6）、式（7）分别代入式（4）、式（5）可解出1A 和1B ：()1112222(1)EabA B q ab v ν+=---()1122222(1)EabB A q ab v ν+=--- 121q q A E ν-=-， 211q q B E ν-=- （8） 122111,q q q q u A x x v B y y E Eνν--==-==- （9）4．分析：把式(8)代入几何和物理方程可求出应力分量，不难验证这些应力分量可以满足平衡微分方程和应力边界条件，即式(8)所示位移为精确解答。

工程塑性力学(第四章)弹塑性力学边值问题的简单实例

工程塑性力学(第四章)弹塑性力学边值问题的简单实例


σθ
−σr
=
2
p
b2 r2
在 r = a 时取最大值，则 r = a 处首先屈服
(σθ
− σ r ) max
=
2
p
b2 a2
=σs
求得弹性极限载荷（压力）为
pe
=
a2σ s 2b2
，
p
=
pe
=
b2 − a2 a2
pe
= σs 2
⎜⎜⎝⎛1 −
a2 b2
⎟⎟⎠⎞
（2）弹塑性解
（4-26）
p > pe 时，塑性区逐渐扩张。设弹、塑性区交界处 r = c ， a < c < b 。
b
弹性区
c
用边界条件σ r r=a = − p ，可确定出 C′ = − p − σ s ln a ，
a
所以
⎪⎧σ r ⎨ ⎪⎩σθ
= σ s ln r − p − σ s ln a = − p + σ s
=σs
+σr
=
−p
+ σ s (1 +
ln
r) a
ln
r a
（4-27）
塑性区 图 4-3
属静定问题，未用到几何关系。
ΔFi = F&iΔt ， ΔTi = T&iΔt ， Δui = u&iΔt
（4-10） （4-11）
式中 F&i ，T&i 和 u&i 分别称为体力率、面力率和位移率（速度）。引入率的表达形式
可以简化公式表达。 求解过程为：
已知时刻 t 时，位移 ui ，应变 εij ，应力σij ，加载面 f (σij ,ξ ) = 0 。在 ST 上给
弹塑性力学(4)

弹塑性力学(4)

弹性力学土木工程学院许强第四章弹性应力应变关系414243444546474849410411412413引言基本假设假定建立弹性材料模型的必要性定义各向同性材料的线弹性应力应变关系虚功原理弹性固体的应变能和余能密度各向异性线弹性体应力应变关系非线弹性应力应变关系弹性体的唯一性稳定性正交性和外凸性各向同性材料的增量应力应变关系基于割线模量的增量关系变模量增量应力应变模型第四章弹性应力应变关系前面已进行了应力分析和应变分析导出了平衡方程和几何方程
2. 由于真实的位移场（应变场）必须满足位移边界条件，故真实位移场（应 变场）应视为可能位移场（应变场）的家族成员之一。而对于真实位移场 （应变场）还必须满足“应变协调条件”，即应变可积分条件。 3. 一般而言，与满足位移边界条件的连续变形相协调的位移模式有无限多个。 但对于给定的问题，同时又满足应变协调的位移模式仅存在一个，即真实 位移场仅有一个。 4. 在弹性力学问题的求解思路通常有两种：（a）按应力求解，（b）按位移 求解。而仅当按应力求解时才用到应变可积分条件，即式（4.2b）。
§4.4 定义
弹性材料
当一块材料受力后就会变形，如果施加的力撤除后，物体即恢复它原来的形状和 大小，那么这种材料就可称为弹性的。从数学上来说，这种材料的本构方程为：
σij = Fij (εkl )
(4.3)
其中， Fij为弹性响应函数，因此，由上式描述的弹性性能为既可逆又与路 径无关，即应变仅由当前应力状况所决定，反之亦然。上述定义的弹性材 料通常称为Cauchy弹性材料。 在特定的加载－卸载循环下，Cauchy弹性材料可产生能量，显然这是 与热力学定律相违背的。为此，采用术语超弹性或Green弹性材料去表明 式（4.3）中的弹性影响函数进一步受到弹性应变能函数W存在的限制。 一般而言，W是应变分量的函数，即
弹塑性力学第四章

弹塑性力学第四章



x

y
)
2019/7/26
36
§4-3 各向同性材料弹性常数

yz

2(1 )
E
yz

xy

2(1
E
)

xy

zx

2(1
E
)
zx
采用指标
符号表示：
ij

1 E
(1 ) ij
ij kk
ij

E
1
ij
1 2
ij kk
2G
0 0 0

2G
0
0
0


2G 0 0 0

2G 0
0

对
称
2G 0



2G
2019/7/26
31
§4-3 各向同性材料弹性常数
3.1 本构关系用、G表示
采用指标符号表示：
ij 2Gij ij kk 2Gij iⅠj
2019/7/26
16
§4-2 线弹性体的本构关系
2.1 各向异性材料 Eijkl 减少为66=36个独立系数，用矩阵 表示本构关系
{}=[c]{}
11
22
33
23
31
T 12
11
22
33
23
31
T 12
x3 弹性主轴
材料主轴，并取另一坐标
系x’i ，且x’1 = x1，x’2=x2，
x2
x’3=-x3。在两个坐标下，
弹塑性力学第四章弹性本构关系资料

弹塑性力学第四章弹性本构关系资料

产生的x方向应变：
产生的x方向应变：
叠加
产生的x方向应变：
同理：
剪应变：
物理方程：
说明：
1.方程表示了各向同性材料的应力与应 变的关系，称为广义Hooke定义。也称 为本构关系或物理方程。
2.方程组在线弹性条件下成立。
. 体积应变与体积弹性模量
令： 则： 令：
sm称为平均应力; q 称为体积应变
eij
1 2G
sij
(4.40)
因为 J1 0, J1' 0 ,所以以上六个式子中独立变量只有5个
因此应力偏张量形式的广义虎克定律，即
eij
1 2G
sij
em
1 3K
sm
(4.41)
用应变表示应力：
或： ✓ 各种弹性常数之间的关系
§4-2 线弹性体本构方程的一般表达式
弹性条件下，应力与应变有唯一确定的对应关系，三维 应力状态下，一点的应力取决于该点的应变状态，应力是应 变的函数（或应变是应力的函数） 6个应力分量可表述为6个应变分量的函数。
式（２）中的系数 有３６个．
称为弹性常数，共
由均匀性假设，弹性体各点作用同样应力 时，必产生同样的应变，反之亦然．因此 为 常数，其数值由弹性体材料的性质而定．
式（２）推导过程未引用各向同性假设， 故可适用于极端各向异性体、正交各向异性体、 二维各向同性体以及各向同性体等．
式（２）可用矩阵表示
式(3)可用简写为 称为弹性矩阵.
三、. 弹性常数
1. 极端各向异性体:
物体内的任一点, 沿各个方向的性能都不相 同, 则称为极端各向异性体. (这种物体的材料极 少见)
即使在极端各向异性条件下, 式(2)中的36个 弹性常数也不是全部独立.
弹塑性力学 第四章 弹性力学的求解方法

弹塑性力学 第四章 弹性力学的求解方法


说明： 1、数学上可证明, 当为线弹性小变形情况，求解的 基本方程和边界条件为线性，叠加原理成立。 2、对大变形情况，几何方程出现二次非线性项，平 衡微分方程将受到变形的影响，叠加原理不再适 用。 3、对非线弹性或弹塑形材料，应力应变关系是非线 性的，叠加原理不成立。 4、对载荷随变形而变的非保守力系或边界为
1. 位移法：将几何方程代入物理方程，得到用位移
表示的应力分量，再将应力分量代入平衡方程和应力边 界条件，即得到空间问题的位移法控制方程。不需要用 相容位移表述。 3个位移表述的平衡微分方程，包含3个位 移未知数。 结合边界条件，解上述方程，可求出位移分 量，由几何方程求应变，再由本构方程求应力。
第四章 弹性力学问题的求解方法
§7-1 弹性力学基本方程
1. 平衡微分方程方程
2. 几何方程
3. 物理方程
各种弹性常数之间的关系
4. 相容方程
• 求解物理量：6个应力分量 6个应变分量 3个位移分量
共15个未知量
用于求解的方程：平衡微分方程 3个 几何方程 6个
共15个方程
本构方程
6个
用非线性弹簧支承的情况，边界条件是非 线性的，叠加原理也将失效。
二. 解的唯一性定理：
在给定载荷作用下，处于平衡状态的弹性体， 其内部各点的应力、应变解是唯一的，如物体刚 体位移受到约束，则位移解也是唯一的。 无论何方法求得的解，只要能满足全部基本方 程和边界条件，就一定是问题的真解。
三.圣维南原理: 提法一：若在物体的一小部分区域上作用一自平衡力系，则 此力系对物体内距该力系作用区域较远的部分不产生 影响只在该力系作用的区域附近才引起应力和变形。 提法二：若在物体的一小部分区域上作用一自平衡力系，该 力系在物体中引起的应力将随离力系作用部分的距离 的增大而迅速衰减，在距离相当远处，其值很小，可 忽略不计。 提法三：若作用在物体局部表面上的外力，用一个静力等效 的力系(具有相同的主矢和主矩)代替，则离此区域较 远的部分所受影响可以忽略不计。
弹塑性力学第四章 弹性本构关系

弹塑性力学第四章 弹性本构关系

E K 3(1 2 )
(4.36) (4.37) (4.38)
K称为体积弹性模量，简称体积模量。
因此
q
sm
K
,em
sm
3K
1 3 1 1 ex e x e m ( sx sm) sm sx E E 3K 2G
1 ey e y e m sy 2G
1 eij sij 2G
(4.40)
1 eij sij 2G 1 em sm 3K
(4.41)
用应变表示应力：
或：
各种弹性常数之间的关系
§4-2 线弹性体本构方程的一般表达式
弹性条件下，应力与应变有唯一确定的对应关系，三维 应力状态下，一点的应力取决于该点的应变状态，应力是应 变的函数（或应变是应力的函数） 6个应力分量可表述为6个应变分量的函数。
• 材料的应力与应变关系需通过实验确定的。 • 本构方程实际是应力与应变关系实验结果的数学 描述。 • 由于实验的局限性，通常由简单载荷实验获得应 力与应变关系结果，建立描述相应的数学模型， 再将数学模型用于复杂载荷情况的分析。（用一 定实验验证结果）
• 例如：材料单轴拉伸应力-应变z e m sz 2G
1 1 1 1 yz s yz exy e xy xy sxy eyz e yz 2G 2G 2G 2G
1 1 exz e xz xz sxz 2G 2G
整理以上六个式子，得 整理以上六个式子，得
因为 J1 0, J1' 0 ,所以以上六个式子中独立变量只有5个 因此应力偏张量形式的广义虎克定律，即
物理方程：
s ij 3 1 3 e ij s ij s m ij s m ij E E 2G E
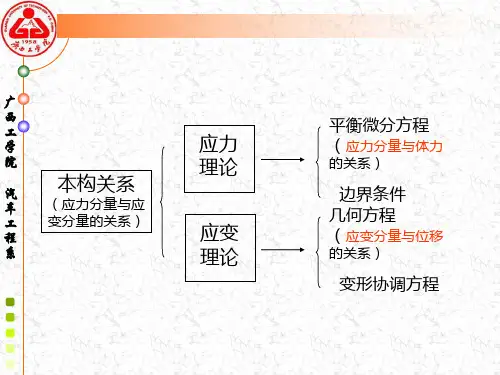
弹塑性力学第四章

弹塑性力学第四章


y c21 x c22 y c23 z z c31 x c32 y c33 z
x 对 x 的影响应与 y 对 y 及 z 对 z 的影响相同，即 c11 c22 c33
y , z 对 x 的影响应相同，即 同理，
因而有：
c12 c13
c11 c22 c33 a c12 c21 c13 c31 c23 c23 b
对于应变主轴，弹性常数只有两个。
广义胡克定律
各向异性弹性体独立的常数有21个。 系数矩阵对称 Cmn Cnm 广 西 工 具有一个弹性对称面的各向异性弹性体的独立常数有13个。 学 院
广义胡克定律
x x , y y , z z , xy xy , yz yz , xz xz
广 西 工 学 院 汽 车 工 程 系
x x , y y , z z , xy xy , yz yz , xz xz
广 西 工 学 院
x 汽 x 车 工 2 2 2 x l11 y l12 z l13 2 xy l11l12 yz l12l13 xz l11l13 x x 程 系 ,
y y z z
z
y
y
z
ij liil jj ij
车 工 程 系
弹性对称面：如果物体内存在这样一个平面，和该平面对称的 汽 两个方向都具有相同的弹性，则该面称为物体的弹性对称面。 弹性主方向：垂直于弹性对称面的方向 具有三个弹性对称面的各向异性弹性体（正交各向异性）的 独立常数有9个。
广义胡克定律
证明：正交各向异性弹性体的独立常数有9个。 证明：取弹性主轴为三个坐标轴，将z轴旋转180度
弹塑性力学第04章

弹塑性力学第04章


x=rcosθ y=rsinθ z=z
图（4-1）
1．平衡微分方程



在轴对称情况下，由于方向的 对称性，切应力τ θ z=τ zθ =0， τ rθ =τ θ r=0； 应力分量σ r，σ θ ，σ z，τ zr， 均为r与z的函数； 体力分量只有沿r与z方向的Fr 与Fz； 则可得r与z方向的平衡微分方 程：
4.边界条件
（1）侧面边界上
dy l , ds
f x f y f z 0 外法线n的方向余弦为 dx m , n0 ds
将6个应力分量代入应力边界条件，前两式自然满足，而第三式为
dx dy d 0 x ds y ds ds
则积分后可得φ=K （在横截面周界c上） 其中，K为常数。对单连通区域（实心杆），可以取K=0，即
φ（x,y）=0 （在横截面周界c上） （4-18）
这是因为，由式（4-17）可知，当扭转应力函数φ相差一个常数K 时，对求应力分量无影响。
（2）端面边界条件（以上端面为例）
R zydxdy 0 R ( x zy y zx )dxdy M R
zr
r
2 2 2 2 z 2 2 1 2 z
（4-7）
能够满足式（4-6）的双调和函数列出如下：
五次幂 四次幂 三次幂 二次幂 一次幂 零次幂 负一次幂 负二次幂 负三次幂 r 2 z 3r 2 4 z 2 , z 3 5r 2 2z 2 2 2 2 2 2 2 r r 4z , z 3r 2z 2 3 3 r z, z , z ln r z 2 lnr R, zlnr,zlnR z -1 R z zR , ln R -1 zR -3 2 2 5 r 2z R
弹塑性力学___第四章_弹性力学的求解方法

弹塑性力学___第四章_弹性力学的求解方法


叠加原理：弹性体受几组外力同时作用时的解等于每一组外力单 独作用时对应解的和。
叠加原理成立的条件：小变形条件（平衡、几何方程才 为线性的），弹性本构方程（虎克定律）。
4-5塑性力学最简单的问题、求解塑性力学的问题
在塑性力学中，有些问题在平衡方程和屈服条件 中的未知函数和议程式的数目相等，因而结合边 界条件一般便可找出弹塑性体或结构中应力分布 的规律。而应变和位移再根据本构方程和几何方 程或连续性条件分别求出。这种仅通过平衡方程、 屈服条件就能完全确定应力场的问题属静定问题 （称为塑性力学最简单问题）
（2）应变协调方程（变形连续必条件）（变形相容条件）
可缩写为：
上述方程是六个应变分量 保证三个位移分量 连续函数（保持连续）的条件。 为单值
3、本构方程（物性方程）
（1）在弹性变形阶段，且屈服函数 则有
如用应变表示应力，则有
为了与塑性变形本构方程对比，也可将本构方程表示为
（2）在弹塑性变形阶段，屈服函数
1. 平衡（或运动方程）
若等式右式不等零，即表示物体内质点处于运动状态， 则根据理论力学中的达朗伯原理需将上式右端等于括号 内的惯性力项。 方程只表明物体内一点的应力状态与其邻点的应力 状态之间在平衡（或运动）时所满足的关系。
2. 几何方程与应变协调方程
（1）几何方程
此式表明在小变形条件下，物体内一点附近的变形情况和该点的 应变状态之间的关系。
第四章 弹塑性力学基础理论的建立及基本解法
§4-1 弹塑性力学基本理论的建立 弹塑性力学的任务：研究各种具体几何尺寸的
弹性、弹塑性体或刚塑性体在各种几何约束及 承受不同外力作用时、发生于其内部的应力分 布与变形（或位移）规律。
与材料力学一样，弹塑性力学所求解的大多 数问题是超静定问题，因此其基础理论的 建立来自三个方面的客观规律：平衡方 程 ；几何方程 ；本构方程
弹塑性力学第四章弹性力学的求解方法

弹塑性力学第四章弹性力学的求解方法


微分方程并求解，最后根据边界条件确定待定常数。
逆解法求解空间问题
逆解法的基本思想
从已知的空间应力或位移函数出发，反推得到弹性体的形状和边界条件。
适用于具有特定应力或位移分布的空间问题
如无限大体、半无限大体等具有特殊应力或位移分布的空间问题。
求解步骤
假设空间应力或位移函数，根据弹性力学基本方程推导得到弹性体的形状和边界条件，并 验证假设的合理性。
04
半解析法在弹性力学中的应用
有限差分法基本原理及步骤
差分原理
有限差分法基于差分原理，将连续问 题离散化，通过求解差分方程得到近 似解。
网格划分
将求解区域划分为规则的网格，每个 网格节点对应一个未知数。
差分格式
根据问题的性质和精度要求，选择合 适的差分格式，如向前差分、向后差 分、中心差分等。
边界处理
电测实验方法介绍及优缺点分析
电阻应变片法
利用电阻应变片将试件表面的应变转换 为电阻变化，通过测量电路获取应变信 息。该方法具有测量精度高、稳定性好 、适用于各种环境和试件形状的优点， 但需要粘贴应变片并进行温度补偿，且 只能进行点测量。
VS
电容传感器法
利用电容传感器将试件表面的位移或应变 转换为电容变化，通过测量电路获取相关 信息。电容传感器法具有非接触、高灵敏 度、宽频响等优点，但易受环境干扰，且 需要进行复杂的电路设计和信号处理。
04 边界条件处理 根据边界条件对总体刚度矩阵和荷载向量进行修正。
05
求解线性方程组
求解总体刚度矩阵和荷载向量构成的线性方程组，得 到节点位移。
边界元法基本原理及步骤
边界积分方程
边界离散化
单元分析
总体合成
求解线性方程组

第四章-弹塑性断裂力学PPT课件


a* 2a
18
3.材料加工硬化的修正
考虑材料加工硬化，当 s 200 ~ 400MPa 时，低
碳钢取
f
1 2
(
s
b)
代替 s 。其中 f
为流变应力。
b 为材料的抗拉强度。
综合考虑上述3部分内容
D－B模型的计算公式
8 f a* ln sec[ (M )]
E
2 f
19
§4.5 J积分的定义和特性
主要包括COD理论和J积分理论.
3
§4.1 小范围屈服条件下的COD 一.COD
COD(Crack Opening Displacement) 裂纹张开位移。 裂纹体受载后，裂纹尖端附近的塑性区导致裂纹尖端表面 张开——裂纹张开位移：表达材料抵抗延性断裂能力
c —COD准则
裂纹失稳扩展的临界值
第四章 弹塑性断裂 力学
线弹性断裂力学 脆性材料或高强度钢所发生的脆性断裂 小范围屈服：塑性区的尺寸远小于裂纹尺寸
弹塑性断裂力学 大范围屈服:端部的塑性区尺寸接近或超过裂纹尺寸，
如：中低强度钢制成的构件． 全面屈服：材料处于全面屈服阶段，如：压力容器的
接管部位.
2
弹塑性断裂力学的任务：在大范围屈服下，确定能定 量描述裂纹尖端区域弹塑性应力，应变场强度的参量．以 便利用理论建立起这些参量与裂纹几何特性、外加载荷之 间的关系，通过试验来测定它们，并最后建立便于工程应 用的断裂准则。
( 12
x1
22
x2
)
u2 x1
11
2u1 x12
12
2u2 x12
21
2u1 x1x2
22
2u2 x1x2
)]dx1dx2

弹塑性力学-04


x E y
其中E为弹性常数，这就是熟知的 胡克定律。
在三维应力状态下，描绘一点处的 应力状态需要9个应力分量，与之 相应的应变状态也要用9个应力分 量来表示。在线弹性阶段，应力与 应变间仍有线性关系存在，但在一 般情况下，任一应变分量要受9个 应力分量 制约。
3
由于应力张量与应变张量的对称性
10
x e 2 x , xy xy
y e 2 y , yz yz z e 2 z , zx zx
x x ( y z ) (3 2 ) 2 (3 2 )
正交各向异性的弹性材料的本构关系，可根据任一坐标轴 反转时弹性常数保持不变的要求
c12 x c22 y c23 z c11 , c22 , c33 , c12 , c13 , c23 , c44 , c55 , c66 c13 x c23 y c33 z c44 xy 共9个弹性常数 c55 yz c66 zx
1 x ( x v y ) E 1 y ( y v z ) E v z ( x y ) E 1 xy xy G
如用应变分量表示应力分量
14
对于平面应变问题
z yz zx 0
E x [(1 v) x v y ] (1 v)(1 2v) E y [v x (1 v) y ] (1 v)(1 2v) vE z ( x y ) (1 v)(1 2v) xy G xy
c 41 x c 42 y c 43 z c 44 xy c 45 yz c 46 zx c51 x c52 y c53 z c54 xy c55 yz c56 zx c61 x c62 y c63 z c64 xy c65 yz c66 zx

弹塑性力学-第四章


ur
u r ur dr r A A
x
径向线段PA的转角： 线段PB的相对伸长： 环向线段PB的转角：
1
1 0
PB PB (r ur )d rd u r （c） PB rd r
（b）
tan 1 1
ur (ur d ) ur BB PP 1 u r （d） PB r rd
剪应变为：
1 ur r
（d）
r 1 1 1 1 ur r
（e）
(2) （P,A,B）只有环向位移， 无径向位移
径向线段PA的相对伸长：
O

PA PA dr dr r 2 PA dr 0
径向线段PA的转角： （f）
r P d
2 X Y 2 2 2 ( x y ) (1 ) x y y x
2 2 2 2 ( x y ) 0 x y 4 4 4 4 4 2 2 2 4 0 x x y y
r r
d
r
P r
x
(r dr )d dr A k r r r dr r k
将上式化开：
r rd
O r r rdrd ddr r drd r

drd kr rdrd 0
两边同除以
（h）
环向线段PB的转角：
剪应变为：
r 2
u u 2 2 r r
u 2 r
（i） （j）
(3) 总应变(是指同时存在径向、环向位移的一般情形)
ur u r 0 r r1 r 2 r r ur 1 u 1 2 r r 1 ur u u r r 1 r 2 r r r u r r r ur 1 u r r

第四章 弹性变形、塑性变形、本构方程


弹性变形特点: ⑴ 弹性变形特点:
弹性变形是可逆的。物体在变形过程中， ① 弹性变形是可逆的。物体在变形过程中，外力所做 的功以能量（应变能）的形式贮存在物体内， 的功以能量（应变能）的形式贮存在物体内，当卸 载时，弹性应变能将全部释放出来， 载时，弹性应变能将全部释放出来，物体的变形得 以完全恢复； 以完全恢复； 无论材料是处于单向应力状态，还是复杂应力态， ② 无论材料是处于单向应力状态，还是复杂应力态， 在线弹性变形阶段，应力和应变成线性比例关系； 在线弹性变形阶段，应力和应变成线性比例关系； 对材料加载或卸载，其应力应变曲线路径相同。 ③ 对材料加载或卸载，其应力应变曲线路径相同。 因此，应力与应变是一一对应的关系。 因此，应力与应变是一一对应的关系。
◆ 理想线性强化刚塑性力学模型
理想线性强化刚 塑性力学模型， 塑性力学模型，其 应力应变关系的数 学表达式为： 学表达式为：
σ = σ s + E1ε
弹塑性力学
(当ε ≥ 0时)
（4--5）
常用简化力学模型（ §4-2 常用简化力学模型（续7）
◆ 幂强化力学模型 为了避免在 ε = ε s 处 的变化， 的变化，有时可以采用幂 强化力学模型。 强化力学模型。当表达式 中幂强化系数 n 分别取 0 或 1 时，就代表理想弹塑 性模型和理想刚塑性模型。 性模型和理想刚塑性模型。 其应力应变关系表达式为： 其应力应变关系表达式为：
弹塑性力学
弹性变形与塑性变形的特点、塑性力学的附加假设（ ） §4-1 弹性变形与塑性变形的特点、塑性力学的附加假设（续3）
塑性变形特点: ⑵ 塑性变形特点:
塑性变形不可恢复，所以外力功不可逆， ① 塑性变形不可恢复，所以外力功不可逆，塑性变形的产生必 定要耗散能量（称耗散能或形变功）。 定要耗散能量（称耗散能或形变功）。 在塑性变形阶段，其应力应变关系是非线性的。 ② 在塑性变形阶段，其应力应变关系是非线性的。由于本构方 程的非线性，所以不能使用叠加原理。 程的非线性，所以不能使用叠加原理。又因为加载与卸载的 规律不同， 应力与应变之间不再存在一一对应的关系， 规律不同， 应力与应变之间不再存在一一对应的关系，即 应力与相应的应变不能唯一地确定， 应力与相应的应变不能唯一地确定，而应当考虑到加载路径 （或加载历史）。 或加载历史）。 在载荷作用下，变形体有的部分仍处于弹性状态称弹性区， ③ 在载荷作用下，变形体有的部分仍处于弹性状态称弹性区， 有的部分已进入了塑性状态称塑性区。在弹性区， 有的部分已进入了塑性状态称塑性区。在弹性区，加载与卸 载都服从广义虎克定律。但在塑性区， 载都服从广义虎克定律。但在塑性区，加载过程服从塑性规 而在卸载过程中则服从弹性的虎克定律。 律，而在卸载过程中则服从弹性的虎克定律。并且随着载荷 的变化，两区域的分界面也会产生变化。 的变化，两区域的分界面也会产生变化。 依据屈服条件，判断材料是否处于塑性变形状态。 ④ 依据屈服条件，判断材料是否处于塑性变形状态。 弹塑性力学

弹塑性力学-第4章_本构方程

第四章本构方程在前面的章节中，已经建立了变形体的平衡微分方程和几何方程，分别是从静力学方面和从几何学方面考察了变形体的受力和变形。

但是只有这些方程还不足以解决变形体内的应力和变形问题。

对于变形体，未知变量包括6个应力分量，6个应变分量和3个位移分量，一共有15个未知函数，而平衡方程和几何方程一共是9个，未知函数的个数多于方程数。

因此还必须研究物体的物理性质，即应力与应变之间的关系。

通常称这种关系为变形体的本构方程，或称为物性方程。

塑性本构包括三个方面：1、屈服条件，2、流动法则，3、硬化关系；其中屈服条件：判断何时达到屈服，流动法则：屈服后塑性应变增量的方向，也即各分量的比值，硬化规律：决定给定的应力增量引起的塑性应变增量大小。

以上构成塑性本构关系。

4.1弹性应变能函数变形固体的平衡问题不仅需要运动微分方程、应变—位移方程(即变形几何方程)还需要将应变分量和应力张量分量联系起来，方能给定物体的材料抵抗各种形式变形的规律。

该规律的理论解释需要对分子间力的本质有深入的认识，该分子力力图使固体粒子间保持—定的距离，也就是需要对固体中应力分量和应变分量有深入的认识。

这种作用机理在非常接近稳定状态的气体中己弄清楚，但对于弹性体情况，目前科学技术发展水平还不能解决这一难题。

如要通过实验探求物体内部的应力和应变的关系，则总是从一些量的测量来推理得到，在一般情况下，这些量并非应力或应变的分量(例如平均应变、体积压缩、物体表面一线元的伸长等等)．因此，在现时应力与应变关系主要是通过直接实验建立。

然而该关系中的某些固有的一般特性可以在理沦上加以说朋，如能量守恒定律为应力-应变关系的理论研究提供了基础。

1.1应变能密度假设变形的过程是绝热的，也就是在变形过程中系统没有热的损失，而且假设物体中任意无穷小单元改变其体积和形状所消耗的功与其从未变形状态到最终变形状态的转换方式无关。

这个条件是弹性的另一种定义。

换句话说，就是假设物体粒子互相作用过程中的耗散(非保守)力的作用与保守力的作用相比是可以忽略的。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

代入广义胡克定律
x c11 x c12 y c13 z c14 xy c15 yz c16 zx
x c11 x c12 y c13 z c14 xy c15 yz c16 zx
c11 x c12 y c13 z c14 xy c15 yz c16 zx
b
广义胡克定律
由应力分量的坐标变换公式（2-20）可得：
广 西 工 学 院 汽 车 工 程 系
xy l11l22 xy xy 2 x l11 x x 2 y l22 y y 2 z l33 z z
上述关系式是胡克（Hooke）定律在复杂应力条件下 的推广，因此又称作广义胡克定律。
广义胡克定律
广义胡克定律的张量表示： ij cijkl kl cijkl 称为弹性系数，一共有36个。
i, j, k , l 1, 2.3
广 西 工 学 院 汽 车 工 程 系
如果物体是非均匀材料构成的，物体内各点受力后将 有不同的弹性效应，因此一般的讲，cmn 是坐标x，y，z 的函数。 如果物体是由均匀材料构成的，那么物体内部各点， 如果受同样的应力，将有相同的应变；反之，物体内各 点如果有相同的应变，必承受同样的应力。 因此cmn为弹 性常数，与坐标无关。 各向同性材料，独立的弹性常数只有两个。
xy yz zx
xy
G
yz
G
zx
G
式中， G
E 2 1 v
为各向同性物体的剪切弹性模量。
表示材料弹性性能的常数有3个，但只有两个是独立的。 张量记法：
1 v v ij ij E E vE ij e E ij ij 1 v 1 v 1 2v
同理可得： yz 0, zx 0
因此，对于各向同性弹性体，主应变方向必为主应力方向。
广义胡克定律
证明：各向同性均匀弹性体的弹性常数只有两个。
广 西 工 学 院 汽 车 工 程 系
证明：令坐标轴与主应力方向一致，则主应力与主应变间 的关系为： c c c
x 11 x 12 y 13 z
广义胡克定律
二、各向同性弹性体广义胡克定律的几种形式 令坐标轴与主应力方向一致，则
广 西 工 学 院 汽 车 工 程 系
x c11 x c12 y c13 z y c21 x c22 y c23 z z c31 x c32 y c33 z
(2-20)
xy l21l31 x l22l32 y l23l33 z
xy l11l22 l12l21 yz l12l23 l13l22 xz l13l21 l11l23 xy
yz yz , xz xz
1 1
xy xy xy xy xy xy
i j i j
2 e 2 2 3 e 2 3
坐标变换
y e 2 y , z e 2 z ,
, 称为拉梅弹性常数。
1, ij ij e 2 ij , = 0,
c11 c22 c33 a c12 c21 c13 c31 c23 c23 b
令 a b 2 , b , e 1 2 3 ,则 1. 弹性拉梅弹性常数表示的广义胡克定律 x e 2 x , e 2
广 西 工 学 院
x 汽 x 车 工 2 2 2 x xl11 y l12 z l13 2 xy l11l12 yz l12l13 xz l11l13 x 程 系 y y , z z
z
y y
z
ij lii l jj ij
x
E
（4-6，4-7）
x
x
比较以上式子可知：
E
3 2 ,v 2
广义胡克定律
代入广义胡克定律，得
广 西 工 学 院 汽 车 工 程 系
1 x x v y z , E 1 y y v x z , E 1 z z v x y , E
ij
广义胡克定律
3. 用应力偏量和应变偏量表示的广义胡克定律
广 西 工 学 院 汽 车 工 程 系
m
1 x y z x y z x y z 3 3E 1 1 1 2 1 2 x y z m m 3K 3E E
应力 理论 应变 理论
平衡微分方程 （应力分量与体力
的关系）
边界条件 几何方程 （应变分量与位移
的关系）
变形协调方程
广 西 工 学 院 汽 车 工 程 系
广义胡克定律
广义胡克定律
一、广义胡克定律
广 西 工 学 院 汽 车 工 程 系
大量实验表明，在许多工程材料的弹性范围内，单向的应 力和应变之间存在着线性关系： E 材料的变形属性与坐标无关。
广义胡克定律
2. 用弹性模量和泊松比表示的广义胡克定律 将（4-3）式中的应变解出来，可得 x e 2 x x x x y 3 2 2 3 2 （4-5） y e 2 y
因而有：
c11 c22 c33 a
c12 c13
c12 c21 c13 c31 c23 c23 b
对于应变主轴，弹性常数只有两个。
广义胡克定律
各向异性弹性体独立的常数有21个。 系数矩阵对称 Cmn Cnm 广 西 工 具有一个弹性对称面的各向异性弹性体的独立常数有13个。 学 院
m
e x y z 3 m
ij ij e 2 ij
1 m 3K 2 K 3
对比等式两边，可得： sij 2Geij
广义胡克定律
广义胡克定义可写为
m 3K m
sij 2Geij
广 物体的变形可分为两部分：一部分是各向相等的正应力引起的 西 工 相对体积改变；一部分是应力偏量引起的物体几何形状的变化。 学 V 院
广义胡克定律
x x , y y , z z , xy xy , yz yz , xz xz
广 西 工 学 院 汽 车 工 程 系
x x , y y , z z , xy xy , yz yz , xz xz
根据正交各向异性弹性体的性质可知： x x
对比以上两式可得：
c15 c15 , c16 c16 c15 c16 0
同理可得：
c25 c26 c35 c36 c45 c46 0
广义胡克定律
将x轴旋转180度，采用和前面相同的方法，可得：
c14 c24 c34 c56 0
广 西 工 学 院 汽 车 工 程 系
z z
x
y y
将y轴旋转180度，可得： 与前一步骤相同
c14 c24 c34 c56 0
x
如果三个相互垂直的平面中有两个是弹性对称面，则第 三个平面必然也是弹性对称面。
c11 c12 c13 c22 c23 c33 c 对 称 0 0 0 c44 0 0 0 0 c55 0 0 0 0 0 c66
y y x y 3 2 2 3 2
广 西 工 学 院 汽 车 工 程 系
z e 2 z
E,
分别为杨氏弹性模量和泊松比。
右图所示应力状态时，由材料力学可知：
x x
E , y v
e x y z
三维：应力和应变关系的一般表达式为：
对于小变形问题，上述表达式展开成泰勒级数，并且略 去二阶以上的高阶小量。
初始 应力
广义胡克定律
根据无初始应力的假设，（f 1)0应为零。对于均匀材料， 材料性质与坐标无关，因此函数 f 1 对应变的一阶偏导数为常 数。因此应力应变的一般关系表达式可以简化为
广 西 工 学 院 汽 车 工 程 系
y c21 x c22 y c23 z z c31 x c32 y c33 z
x 对 x 的影响应与 y 对 y 及 z 对 z 的影响相同，即 c11 c22 c33
同理， y , z 对 x 的影响应相同，即
车 工 程 系
弹性对称面：如果物体内存在这样一个平面，和该平面对称的 汽 两个方向都具有相同的弹性，则该面称为物体的弹性对称面。 弹性主方向：垂直于弹性对称面的方向 具有三个弹性对称面的各向异性弹性体（正交各向异性）的 独立常数有9个。
广义胡克定律
证明：正交各向异性弹性体的独立常数有9个。 证明：取弹性主轴为三个坐标轴，将z轴旋转180度
由 (c)式代入 (b)式 ,可得出：
xy c41 x c42 y c43 z
xy c41 x c42 y c43 z
c
b
xy c41 x c42 y c43 z
a
d
比较(a) , (b)可得： xy xy ，所以，必定有 xy 0
x y z


ij sij m ij ij e 2 ij ij 2G eij m ij 2Geij 3 G m ij 3
2