正方体的展开图与相对面分布规律 (1)

具体教学设计方案：运筹帷幄决胜千里——“正方体的展开图”判断技巧教学目标：1、了解长方体面及棱的特点，归纳转化的基本前提。

2、判断正方体的展开图，探究转化的基本路径。

3、感悟数学思想及策略，积累转化的基本经验。

教学重难点：1、判断展开图中的相对面及直角处相邻的棱的特点。

2、正方体的各种展开图如何转化为基本类型。

教学过程：一、探究规律师：同学们好，这节课我们来学习《正方体的展开图》判断技巧。

正方体的展开图因其种类繁多，同学们难以记住。

有没有巧妙的方法能够快速、准确地判断呢？我们先从长方体入手来研究。

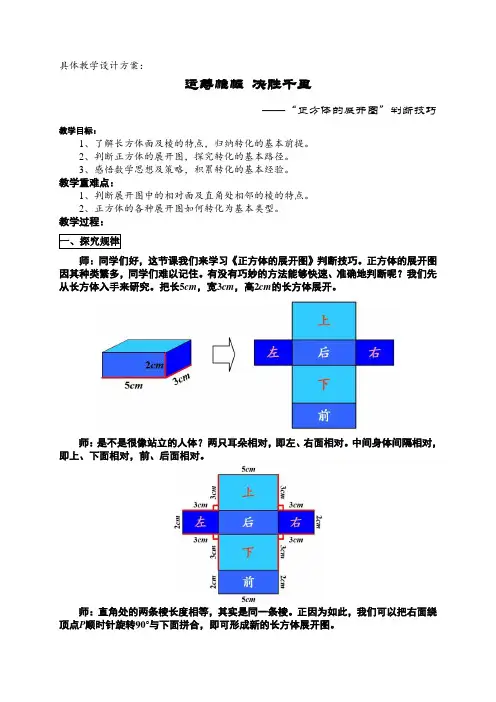
把长5cm，宽3cm，高2cm的长方体展开。

师：是不是很像站立的人体？两只耳朵相对，即左、右面相对。

中间身体间隔相对，即上、下面相对，前、后面相对。

师：直角处的两条棱长度相等，其实是同一条棱。

正因为如此，我们可以把右面绕顶点P顺时针旋转90°与下面拼合，即可形成新的长方体展开图。

小结：①、长方体的任意一条棱都有可能被展开；②、直角处的两条棱长度相等，其实是同一条，所在的面绕顶点旋转后可以互相拼合。

【设计意图：通过长方体的展开图，借助直观人体想象相对的面，突破难点；观察直角处的棱的特征，发现是同一条棱被展开，自然能想到拼合，长方体的展开图就可以转化，产生新的展开图，归纳转化的基本前提。

】二、迁移内化师：根据得出的规律来研究正方体的展开图，下面图形能围成正方体吗？同学们想象一下，耳朵相对，中间身体间隔相对。

师：这就是正方体11种展开图“1－4－1”型中的一种。

【设计意图：直观想象及动画演示正方体展开图的“围拢—展开—旋转”过程，帮助学生进一步理解面的相对性，并通过旋转的简单变式自然过渡到“1－4－1”型展开图的研究，培养学生的空间想象力。

】师：我们先来观察正方体展开图“1－4－1”型的6种类型，就像侧卧的人体。

想象一下，两只耳朵相对，即上、下面相对，中间身体间隔相对，即前、后面相对，左、右面相对。

课程与教学Kechengyujiaoxue如何找正方体展开图的相对面山东省临沂市第十二中学王岚[摘要]寻找正方体展开图的相对面是初中数学的一个考点，本文用“不相邻、三连方中间隔一个和九宫格法”这种方法可以帮助我们简捷、准确地找出正方体展开图的相对面。

[关键词]正方体展开图的相 对面九宫格法正方体的展开与折叠是人教 版数学七年级上册第四章《图形的 初步认识》中的内容，而探索正方 体展开图的相对面分布规律就是 其中的一个考点。

我和学生们通过 对正方体展开图的反复折叠、试 验，总结出确定正方体展开图的相 对面的简单有效的方法，用十六个 字概括是“不相邻、三连方中间隔 一个和九宫格法”。

用这种方法可 以帮助我们简捷、准确地找出正方 体展开图的相对面。

“不相邻、三连方中间隔一 个”，指的是正方体的相对面，一定 不在展开图的相邻位置，如果展开 图中有三个相邻的正方形，那么这 三个正方形中相隔一个的两个正 方形就是相对面。

“九宫格法”适用 于展开图没有三个相邻的正方形 时，以展开图靠中间的正方形为中 心，画出九宫格，这时九宫格圈出 的都是中间正方形的相邻面，那么 落在九宫格外面的正方形与九宫 格正中心的正方形是相对面。

正方体展开图的类型不同找 相对面的方法也有区别，下面针对 正方体展开图的四种类型介绍我 们发现的方法。

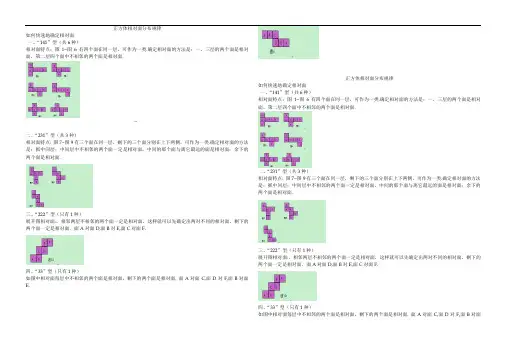
四―”型（中间四连方％两侧各一个，共六种）展开图特点：共三行，中间一 行也是最长的一行有四个正方形 连在一■起，（如图1所东），第一■行和第三行各有一个正方形。

图i相对面的找法：“一四一”型根据“不相邻、三连方中间隔一个”就可以找出所有的相对面。

如图2中，根据“不相邻、三连方中间隔一个”可以知道A Y C是对面图案，B与D是对面图案，那么剩余的E与F就是对面图案。

二、三二”型（中间三连方，两侧各有！、二个，共三种）展开图特点：共三行，中间一行也是最长的一行有三个正方形(如图3)，上下两行各有一个或两个正方形。

正方体相对面分布规律如何快速地确定相对面一、“141”型（共6种）相对面特点：图1~图6有四个面在同一层，可作为一类.确定相对面的方法是：一、三层的两个面是相对面，第二层四个面中不相邻的两个面是相对面.二、“231”型（共3种）相对面特点: 图7~图9有三个面在同一层，剩下的三个面分别在上下两侧，可作为一类.确定相对面的方法是：抓中间层；中间层中不相邻的两个面一定是相对面，中间的那个面与离它最远的面是相对面；余下的两个面是相对面.三、“222”型（只有1种）展开图相对面:，相邻两层不相邻的两个面一定是相对面，这样就可以先确定出两对不同的相对面，剩下的两个面一定是相对面．面A对面D,面B对E,面C对面F.四、“33”型（只有1种）如图中相对面每层中不相邻的两个面是相对面，剩下的两个面是相对面. 面A对面C,面D对F,面B对面E.正方体相对面分布规律如何快速地确定相对面一、“141”型（共6种）相对面特点：图1~图6有四个面在同一层，可作为一类.确定相对面的方法是：一、三层的两个面是相对面，第二层四个面中不相邻的两个面是相对面.二、“231”型（共3种）相对面特点: 图7~图9有三个面在同一层，剩下的三个面分别在上下两侧，可作为一类.确定相对面的方法是：抓中间层；中间层中不相邻的两个面一定是相对面，中间的那个面与离它最远的面是相对面；余下的两个面是相对面.三、“222”型（只有1种）展开图相对面:，相邻两层不相邻的两个面一定是相对面，这样就可以先确定出两对不同的相对面，剩下的两个面一定是相对面．面A对面D,面B对E,面C对面F.四、“33”型（只有1种）如图中相对面每层中不相邻的两个面是相对面，剩下的两个面是相对面. 面A对面C,面D对F,面B对面E.。

正方体表面展开图的专题讲解题型一：判断给定的平面图形是否属正方体表面展开图正方体表面展开图具体说可有以下4类11种图形，如作旋转或翻折后，方向会不同，但相对位置不变,这些不重复计算．1．“一·四·一”型，中间4个连一排，两边各一随便放，共有6种.2．“二·三·一”型,二三相连错一个,三一相连随便放，共3种。

3．“二·二·二”型，阶梯错开放，共1种.4．“三·三”型，共1种。

题型二:找正方体相邻或相对的面.1．从展开图找:（1）相邻的面：①在展开图中有公共边或公共顶点．如;•②在正方形长链中相隔两个正方形．如中A与D.（2)相对的面:①在展开图中同行(或列)中,中间隔一个正方形．如中，A与C，B与D;②和中间一行（或列）•均相连的两正方形亦相对.分析：下列正方体表面展开图的相对面。

想一想下面图1中(1)-（6)是否为正方体的展开图,如果是正方体的展开图，请把 3 、—1 、4 、—2 、7、—5这六个数字分别填入以下正方体的展开图的小正方形格内，使折叠成正方体后，正方体相对面的数字之和都等于2．（1）（2）（3）图1例1、右图中哪两个字所在的正方形,在正方体中是相对的面.例2、在A、B、C内分别填上适当的数．使得它们折成正方体后，对面上的数互为倒数,则填入正方形A、B、C•的三数依次是:（A）12，13，1 （B）13，12，1 (C)1，12，13(D）12，1,13例3、在A、B、C内分别填上适当的数，使它们折成正方体后,对面上的数互为相反数。

例4、找出折成正方体后相对的面。

2．从立体图找：例5、正方体有三种不同放置方式，问下底面各是几？例6、由下图找出三组相对的面。

3、由带标志的正方体图去判断是否属于它的展开图例7、如下图，正方体三个侧面分别画有不同图案，它的展开图可以是（）例8、下面各图都是正方体的表面展开图，若将它们折成正方体，•则其中一个正方体各面图案与其他的不完全一样,它是（)。

正方体找对面的题型一年级一、基础题型（1 - 10题）题1：- 题目：一个正方体展开图如下（简单的1 - 4 - 1型展开图，例如上面一行中间一个正方形，下面一行四个正方形），已知写着数字1的面朝上，数字3的面朝前，问数字1的对面是哪个数字？- 解析：对于正方体的展开图，相对的面是间隔出现的。

在这种1 - 4 - 1型展开图中，1和3中间隔了一个正方形，所以1的对面是3后面的那个面，也就是数字5。

题2：- 题目：正方体展开图（2 - 3 - 1型，上面一行两个正方形，中间一行三个正方形，下面一行一个正方形），数字2的面在左边，数字4的面在上面，问数字2的对面是哪个数字？- 解析：在2 - 3 - 1型展开图中，先看数字2所在的位置。

2的对面是与它不相邻且间隔的面。

数字2与数字4不相邻且间隔，所以2的对面是数字4对面的数字，也就是数字6。

题3：- 题目：正方体展开图（3 - 3型，上下两行各三个正方形），数字1的面在前面，数字3的面在上面，问数字1的对面是哪个数字？- 解析：在3 - 3型展开图里，数字1和数字3是相邻面。

从整体看，1的对面是与1间隔的面，所以1的对面是数字5。

题4：- 题目：有一个正方体，它的六个面上分别标有字母A、B、C、D、E、F。

正方体展开图如下（1 - 4 - 1型），字母A的面在前面，字母C的面在上面，问字母A的对面是哪个字母？- 解析：根据正方体展开图相对面间隔出现的规律，A与C相邻，A的对面应该是与A间隔的面，所以A的对面是字母F。

题5：- 题目：正方体展开图（2 - 3 - 1型），标有红色的面在右边，标有蓝色的面在上面，问红色面的对面是什么颜色的面？- 解析：在2 - 3 - 1型展开图中，红色面在右边，它的对面是与它间隔的面。

蓝色面在上面，红色面的对面就是蓝色面下面的面，假设为绿色面（题目未明确其他颜色的关系，这里假设一种颜色）。

题6：- 题目：一个正方体六个面分别画着苹果、香蕉、橘子、梨、桃、西瓜。

正方体展开图向对面的找法如何找正方体展开图的相对面济宁高新区杨村煤矿中学：赵磊《数学课程标准》中表示：使学生在观测、实验、悖论等数学活动中，辨认出解决问题的方法，体验崭新科学知识的分解成过程。

在本节课的教学中，为学生提供更多了操作方式实验观测的平台，课前使学生搜集了正方体的包装盒，把相对的面涂上相同的颜色，课堂上以剪刀沿棱包住，进行后观测对面的规律。

学生通过对实物模型的操作方式,深入研究各类“进行图”,积极探索它们之中暗含的各种奥秘、规律,概括出来找寻“相对面”的精妙办法:先打听同层外木一面,再打听异层外木两面.剩两面必相对,规律方法妙计献上.（在通过正方体进行图形打听相对面时,首先在同层中三个正方形已连续相连的隔一面找寻,再在异层中外木两面找寻,剩的两面自然相对.）一、“一四一”型展开图；同层中存有已连续的四个正方形，所以优先利用“同层外木一面”找寻对面。

“2”和“4”外木一面“3”就是对面，“3”和“5”外木一面“4”就是对面，剩的“1”和“6”就是对面。

二、“二三一”型展开图图中所含同层已连续三个正方形，利用“同层外木一面”找出“3”和“5”就是对面，剩的利用“异层外木两面”找出“1”和“4”隔着“2”、“3”就是对面，剩的“2”和“6”就是对面。

三、“二二二”型展开图图中不存有同层已连续三个或四个正方形的情况，利用“异层外木两面”的方法找出“1”和“4”隔着“2”、“3”就是对面，“2”和“5”隔着“3”、“4”是对面，剩下的“3”和“6”是对面。

四、“三三”型进行图图中含有同层连续的三个正方形，利用“同层隔一面”的方法，找到“1”和“3”是对面，“4”和“6”是对面，剩下的“2”和“5”是对面。