(完整版)正方体展开图及相对面
- 格式:doc
- 大小:72.51 KB
- 文档页数:3
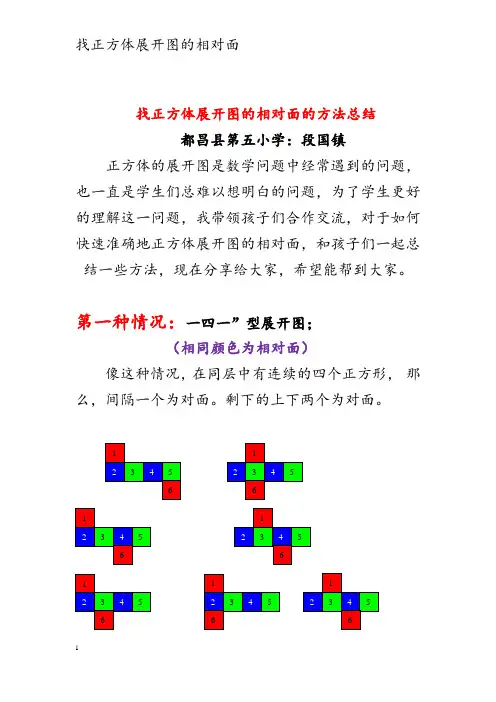
找正方体展开图的相对面的方法总结
都昌县第五小学:段国镇
正方体的展开图是数学问题中经常遇到的问题,也一直是学生们总难以想明白的问题,为了学生更好的理解这一问题,我带领孩子们合作交流,对于如何快速准确地正方体展开图的相对面,和孩子们一起总结一些方法,现在分享给大家,希望能帮到大家。
第一种情况:一四一”型展开图;
(相同颜色为相对面)
像这种情况,在同层中有连续的四个正方形, 那么,间隔一个为对面。
剩下的上下两个为对面。
第二种情况:“二三一”型展开图
这种情况含有同层连续三个正方形,我们也可以利用“同层隔一面”
第三种情况:“二二二”型展开图
图中不存在同层连续三个或四个正方形的情况,利用“异层隔两面”的方法找到“1”和“4”隔着“2”、“3”是对面,“2”和“5”隔着“3”、“4”是对面,剩下的“3”和“6”是对面。
第四种情况:“三三”型展开图
图中含有同层连续的三个正方形,利用“同层隔一面”的方法,找到“1”和“3”是对面,“4”和“6”是对面,剩下的“2”和“5”是对面。
2019年9月。

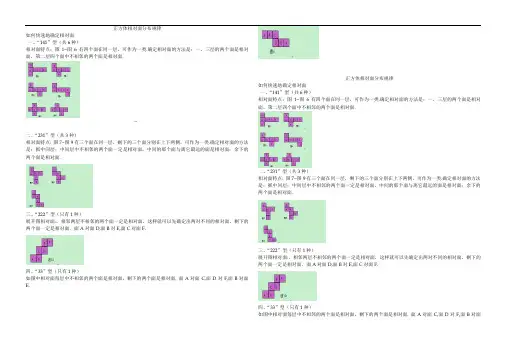
正方体相对面分布规律如何快速地确定相对面一、“141”型(共6种)相对面特点:图1~图6有四个面在同一层,可作为一类.确定相对面的方法是:一、三层的两个面是相对面,第二层四个面中不相邻的两个面是相对面.二、“231”型(共3种)相对面特点: 图7~图9有三个面在同一层,剩下的三个面分别在上下两侧,可作为一类.确定相对面的方法是:抓中间层;中间层中不相邻的两个面一定是相对面,中间的那个面与离它最远的面是相对面;余下的两个面是相对面.三、“222”型(只有1种)展开图相对面:,相邻两层不相邻的两个面一定是相对面,这样就可以先确定出两对不同的相对面,剩下的两个面一定是相对面.面A对面D,面B对E,面C对面F.四、“33”型(只有1种)如图中相对面每层中不相邻的两个面是相对面,剩下的两个面是相对面. 面A对面C,面D对F,面B对面E.正方体相对面分布规律如何快速地确定相对面一、“141”型(共6种)相对面特点:图1~图6有四个面在同一层,可作为一类.确定相对面的方法是:一、三层的两个面是相对面,第二层四个面中不相邻的两个面是相对面.二、“231”型(共3种)相对面特点: 图7~图9有三个面在同一层,剩下的三个面分别在上下两侧,可作为一类.确定相对面的方法是:抓中间层;中间层中不相邻的两个面一定是相对面,中间的那个面与离它最远的面是相对面;余下的两个面是相对面.三、“222”型(只有1种)展开图相对面:,相邻两层不相邻的两个面一定是相对面,这样就可以先确定出两对不同的相对面,剩下的两个面一定是相对面.面A对面D,面B对E,面C对面F.四、“33”型(只有1种)如图中相对面每层中不相邻的两个面是相对面,剩下的两个面是相对面. 面A对面C,面D对F,面B对面E.。


如何快速找正方体的展开面和相对面正方体的展开与折叠是《图形的初步认识》这一章的重要内容,也是近几年中考的热点,而探索正方体的展开图的相对面分布的规律就是其中的一个考点。
下面就谈一谈如何快速地确定相对面,供同学们学习时参考。
一、“141”型(共6种)展开图特点:在这类展开图中,最长的一行(或列)有四个正方形(如图1~6所示)在这种类型中,有4个正方形“直线”相连,其余2个正方形分别在“直线”两旁,位置任意。
相对面特点:图 1~图6有四个面在同一层,可作为一类。
确定相对面的方法是:一、三层的两个面是相对面,第二层四个面中不相邻的两个面是相对面。
二、“231”型(共3种)展开图特点:在这类展开图中,最长的一行(或列)有3个正方形(如图7~9).在“231"型中,“3”所在的行(或列)必须在中间,“2”、“1”所在行(或列)分属两边(前后不分).也就是正方体展开后,如有三个面在“直线”相连,另2个面在“直线”相连面一旁,另一面在它另一旁.故该种情况有3种。
相对面特点: 图7~图9有三个面在同一层,剩下的三个面分别在上下两侧,可作为一类。
确定相对面的方法是:抓中间层;中间层中不相邻的两个面一定是相对面,中间的那个面与离它最远的面是相对面;余下的两个面是相对面.三、“222"型(只有1种)展开图特点:在展正如开图中,最多只有2个正方形“直线”相连。
正如“二面三行,像楼梯”.如图10所示展开图相对面:,相邻两层不相邻的两个面一定是相对面,这样就可以先确定出两对不同的相对面,剩下的两个面一定是相对面.面A对面D,面B对E,面C 对面F。
四、“33”型(只有1种)犹如“三面两行,两台阶”如图中相对面每层中不相邻的两个面是相对面,剩下的两个面是相对面。
面A对面C,面D对F,面B对面E。


11中正方体展开图正方体的十一种平面展开图可记忆成下面口诀:一三二,一四一,一在同层可任意,两个三,日状连,三个二,成阶梯,相邻必有日,整体没有田。
相对的两个面之间总隔着一个面正方体:中间四个面,上下各一面(6种摆法-141)中间三个面,一二隔河见(3种摆法-132/231)中间二个面,楼梯天天见(1种摆法-222)中间没有面,三三连一线(1种摆法-33)例1 在图13中(每个小四边形皆为全等的正方形),可以是一个正方体表面展开图的是( ).例2图14是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C内分别填上适当的数,使得这个表面展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( ).A.0,-2,1B.0,1,-2C.1,0,-2D.-2,0,1例3图15所示的是一个正方体包装盒的表面展开图,各个面上标注的数字分别为1,2,3,4,5,6。
现将表面展开图复原为正方体包装盒,则标注数字1和3的两个面是互相平行的,请你写出另一组相互平行的面上所对应的数字:_______。
注:例1、例2、例3的答案分别为:C;A;2与5或4与6。
是不是有点多此一举?例4 一个无盖的正方体纸盒,将它展开成平面图形,可能情况总共有()。
A.12种 B.11种 C.9种 D.8种千万注意,你可不要选B呦!选D才对。
我又在炫耀了,不过你能很快画出这8个平面展开图吗?下面是示意图,黑方块表示展开图,白方块表示空缺。
(一)□■□■■■□■□(二)■■■■■□□□(三)■■■■□■□□(四)■■■■□□■□(五)■■■■□□□■(六)□■□■■■□□■(七)□□■■■■□□■(八)■□□■■■□□■。

找正方体展开图的相对面的方法总结
正方体的展开图是一个常见的数学问题,但对于学生们来说,往往难以理解。
为了帮助学生更好地掌握这个问题,我带领孩子们一起总结了一些方法,以便快速准确地找到正方体展开图的相对面。
现在,我将这些方法分享给大家。
第一种情况是“一四一”型展开图。
在这种情况下,如果同一层中有连续的四个正方形,那么间隔一个正方形的位置就是对面,而剩下的上下两个正方形就是对面。
第二种情况是“二三一”型展开图。
这种情况下,如果同一层中有连续的三个正方形,那么同一层中间隔一个正方形的位置就是对面。
第三种情况是“二二二”型展开图。
在这种情况下,不存在同一层中连续三个或四个正方形的情况。
因此,我们需要利用“异层隔两面”的方法来找到相对面。
具体来说,“1”和“4”隔着“2”、“3”是对面,“2”和“5”隔着“3”、“4”是对面,而剩下的“3”和“6”是对面。
通过这些方法,我们可以更快速、准确地找到正方体展开图的相对面。

两招识透正方体展开图的相对面西昌一中俊波外国语学校 范仕军正方体的六个面,两两相对,将正方体沿某些棱剪开,可以得到各种展开图,它们都是由六块相同的小正方形组成的平面图形,你能从平面图中确定原来各个面的相对关系吗?比如说,把右边的两个展开图再围成小正方体,“3”对的是哪个数字?你是怎么判断的?有的同学有较强的空间想像能力,能够在头脑中让小正方形“动”起来,准确判断出各面的相对关系,有的要通过模型或动手折纸片才能确定。
其实,有两个“绝招”,掌握两个法则后,用简单的推理就可以准确确定各种正方体开展图各面的的相对关系。
第一个法则叫“隔空相对”。
展开图中,凡是有三个小正方形排成一排的,那中间隔着一个正方形的两个正方形在正方体中必定相对。
如右图中,“B”与“D”隔着“C”相对,“C”与“E”隔着“D”相对,剩下的“A”和“F”自然相对。
第二个法则叫“邻四对一”。
在一个正方体中,每个面都有四个面与之相邻,另一个面则与之相对,把正方体展开,各面的相邻关系是不会改变的。
如果在展开图中,我们能够确定有四个面与之相邻,则剩下的一个面必然与之相对。
如右图,“D”与“C”、“E”、“F”各有一条公共边,相邻;与“B”有一个公共顶点,也相邻,则剩下的“A”必然与“D”相对。
再根据“隔空相对”知道“C”与“E”相对,剩下的“B”和“F”相对。
654321654321FEDCBAFEDCBA运用这两个法则,解决前面的问题就轻而易举了。
第一个图形中,“3”与“5”是“隔空相对”,“4”和“1”用“邻四对一”判定相对,剩下“2”与“6”相对;第二个图形中,“3”与“6”、“4”和“1”都用“邻四对一”法则确定相对,剩下“2”和“5”自然相对。
你是这样判断的吗?正方体共有11种展开图,除上面涉及的四种,另外七种如下:有时仅需用一个法则,有的同时使用这两个法则,就可以准确确定出正方体展开图中六个正方形的三对相对关系,你可以自己试试,看看这两“招”是否灵验。
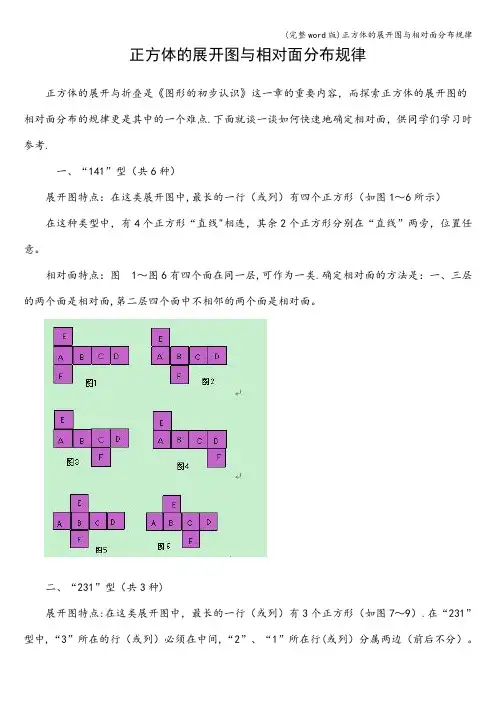
正方体的展开图与相对面分布规律正方体的展开与折叠是《图形的初步认识》这一章的重要内容,而探索正方体的展开图的相对面分布的规律更是其中的一个难点.下面就谈一谈如何快速地确定相对面,供同学们学习时参考.一、“141”型(共6种)展开图特点:在这类展开图中,最长的一行(或列)有四个正方形(如图1~6所示)在这种类型中,有4个正方形“直线"相连,其余2个正方形分别在“直线”两旁,位置任意。
相对面特点:图1~图6有四个面在同一层,可作为一类.确定相对面的方法是:一、三层的两个面是相对面,第二层四个面中不相邻的两个面是相对面。
二、“231”型(共3种)展开图特点:在这类展开图中,最长的一行(或列)有3个正方形(如图7~9).在“231”型中,“3”所在的行(或列)必须在中间,“2”、“1”所在行(或列)分属两边(前后不分)。
也就是正方体展开后,如有三个面在“直线"相连,另2个面在“直线"相连面一旁,另一面在它另一旁.故该种情况有3种。
相对面特点:图7~图9有三个面在同一层,剩下的三个面分别在上下两侧,可作为一类。
确定相对面的方法是:抓中间层;中间层中不相邻的两个面一定是相对面,中间的那个面与离它最远的面是相对面;余下的两个面是相对面。
三、“222"型(只有1种)展开图特点:在展正如开图中,最多只有2个正方形“直线”相连。
正如“二面三行,像楼梯”.如图10所示展开图相对面:,相邻两层不相邻的两个面一定是相对面,这样就可以先确定出两对不同的相对面,剩下的两个面一定是相对面.面A对面D,面B对E,面C对面F。
四、“33"型(只有1种)犹如“三面两行,两台阶”如图中相对面每层中不相邻的两个面是相对面,剩下的两个面是相对面。
面A对面C,面D对F,面B对面E。
正方体展开图向对面的找法
本文介绍如何通过正方体展开图找到相对面的方法。
在教学中,可以让学生收集正方体包装盒,并涂上相同颜色的相对面,然后剪开展开观察对面的规律。
通过实物模型的操作,学生可以深入研究各类展开图,并探索其中的奥秘和规律。
通过归纳总结,可以得出寻找相对面的方法:先找同层隔一面,再找异层隔两面,剩下的两面必相对。
第一种展开图是“一四一”型,其中同层有连续的四个正方形。
利用“同层隔一面”的方法,可以找到“2”和“4”隔着“3”是对面,“3”和“5”隔着“4”是对面,剩下的“1”和“6”是对面。
第二种展开图是“二三一”型,其中同层有连续的三个正方形。
利用“同层隔一面”找到“3”和“5”是对面,剩下的利用“异层隔两面”找到“1”和“4”隔着“2”、“3”是对面,剩下的“2”和“6”是对面。
第三种展开图是“二二二”型,其中不存在同层连续三个或四个正方形的情况。
利用“异层隔两面”的方法找到“1”和“4”隔
着“2”、“3”是对面,“2”和“5”隔着“3”、“4”是对面,剩下的“3”
和“6”是对面。
第四种展开图是“三三”型,其中同层有连续的三个正方形。
利用“同层隔一面”的方法,找到“1”和“3”是对面,“4”和“6”是
对面,剩下的“2”和“5”是对面。
一、正方体的11种展开图
第一类:1+4+1型
中间四连方,两侧各一个,共六种。
第二类2+3+1型
中间三连方,两侧各有一、二个,共三种。
第三类:2+2+2型
第三类:2+2+2型:中间二连方,两侧各有二个,只有一种。
第四类:3+3型:两排各三个,只有一种。
二、正方体展开图找对面口诀法
正方体,展开图,十一种,要记清,
如果要找相对面,记住口诀很简单,
隔面有面是对面,隔面无面就拐弯。
7、箱子、油桶、仓库等所能容纳物体的体积,通常叫做他们的容积。
常用的容积单位有升和毫升也可以写成L 和ml 。
1升=1立方分米 1毫升=1立方厘米 1升=1000毫升
8、a 3读作“a 的立方”表示3个a 相乘,(即a ·a ·a )
【体积单位换算】 高级单位 低级单位 低级单位 高级单位
进率: 1立方米=1000立方分米=1000000立方厘米
1立方分米=1000立方厘米=1升=1000毫升
1立方厘米=1毫升
1平方米=100平方分米=10000平方厘米
1平方千米=100公顷=1000000平方米
×进率 ÷进率
【下载本文档,可以自由复制内容或自由编辑修改内容,更多精彩文章,期待你的好评和关注,我将一如既往为您服务】。
p1.“141型”,中间一行4个作侧面,上下两个各作为上下底面,•共有6种基本图形。
2.“132型”,中间3个作侧面,共3种基本图形。
3.“222型”,两行只能有1个正方形相连。
4.“33型”,两行只能有1个正方形相连。
找“相对面”办法:先找同层隔一面,再找异层隔两面,剩下两面必相对。
(通过正方体展开图找相对面时,首先在同一层四个或三个连续相连的正方形中隔一面寻找,再在异层中隔两面寻找,剩下的两面自然相对。
)
1、如图是一个正方体展开图,和“2”对应的面的是
分析:同层中有连续四个正方形,优先利用“同层隔一面”寻找相对面,2和5隔一面,所以2和5是对面,4和6隔一面,所以4和6是对面,剩下的1和3是对面。
2、如图是一个正方体展开图,与①对应的面的是
分析:含有同层三个连续正方形,优先利用“同层隔一面”寻找,3和5隔一面,所以3和5是对面,再用“异层隔两面”,1和4是对面,剩下2和6是对面。
3、如图是一个的正方体展开图,在正方体中,与2对应的面的是
分析:不存在同层三个或四个连续正方形,利用“异层隔两面”的方法找,2和9是对面。
4、一个正方体的每个都有一个汉字,其平面图展开如图所示,那么在该正方体中和“流”字相对应的字是()
分析:含有同层三个连续正方形,利用“同层隔一面”寻找,防与流是对面
5、如图一个正方体的六面都标上数字,请问5对面是()
1、如图是一个正方体展开图,和“2”对应的面的是第面
2、如图是一个正方体展开图,与①对应的面的是
3、如图是一个的正方体展开图,在正方体中,与2对应的面的是
4、一个正方体的每个都有一个汉字,其平面图展开如图所示,那么在该正方体中和“流”字相对应的字是()
5、如图一个正方体的六面都标上数字,请问5对面是()。