大学物理动生电动势和感生电动势

动生电动势和感生电动势同时存在的试题解题策略电动势的种类及其产生条件电磁感应的条件是闭合回路磁通量发生变化，即ΔΦ变化。

根据变化的情况，电动势可归为三种类型：1.动生电动势：当导体棒切割磁感线运动时，不改变磁感应强度B，但改变了导体棒的截面积S，产生的电动势为E=BLV。

2.感生电动势：当磁感应强度B发生变化时，不改变导体棒的截面积S，产生的电动势为E=n(ΔB/Δt)S。

3.动生电动势和感生电动势同时存在：当闭合回路或闭合回路中部分导体在磁场中做切割磁感线运动同时磁场变化时，产生的感应电动势大小为E=n(ΔΦ/Δt)=n[(S+B)ΔSΔB]/Δt。

其中nB=BLV为动生电动势，nS为感生电动势。

解决同时存在的电动势问题的方法对于第三种情况，两种电动势同时存在，解决问题比较复杂。

在近年的高考模拟试题中，常常出现导体棒切割磁感线的同时磁感应强度强弱也在发生变化的情况。

现介绍两种常用的方法：1.运用E=E1+E2=BLV+n数和。

应注意E1、E2的方向问题，当E1、E2方向相同时，取“+”；当E1、E2方向相反时，取“-”。

方向相同或相反指各自产生的感应电流在回路中流动方向情况。

2.运用E=n(ΔB/Δt)S解答。

即，分别计算出动生感应电动势和感生感应电动势，然后代入公式计算即可。

具体方法是：先任取t时刻，写出Φ(t)表达式，然后求导可得E=Φ'。

两种方式都应掌握，因为在不同的题目中，两种方法的繁简程度有区别。

例题解析题目描述：如图所示，两根平行金属导轨固定在水平桌面上，每根导轨每米的电阻为r=0.10Ω/m，导轨的端点P、Q用电阻可以忽略的导线相连，两导轨间的距离l=0.20m。

有随时间变化的匀强磁场垂直于桌面，已知磁感应强度B与时间t的关系为B=kt，比例系数XXX电阻不计的金属杆可在导轨上无摩擦地滑动，在滑动过程中保持与导轨垂直。

在t=0时刻，金属杆紧靠在P、Q端，在外力作用下，杆以恒定的加速度从静止开始向导轨的另一端滑动，求在t=6.0s时金属杆所受的安培力。

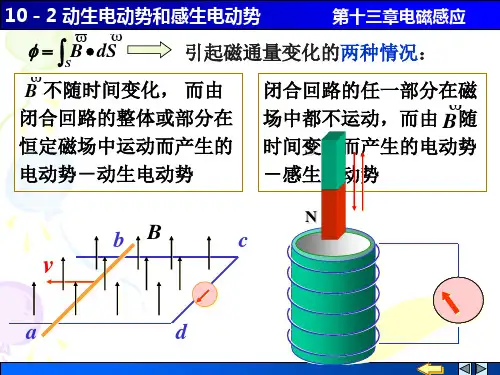
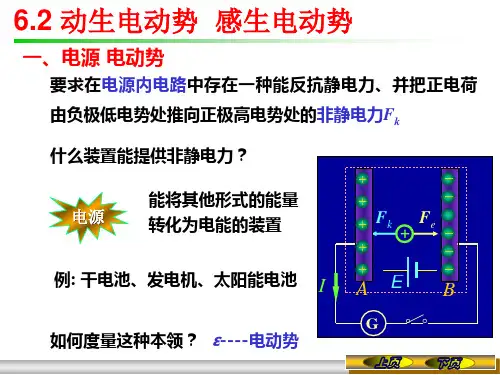
§6-2 动生电动势和感生电动势动生电动势：回路或其一部分在磁场中的相对运动所产生的感应电动势。

感生电动势：仅由磁场的变化而产生的感应电动势。

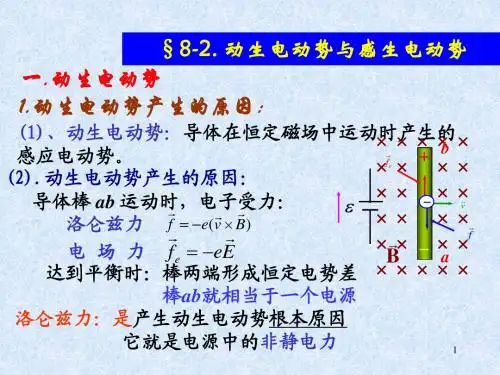
一 动生电动势图6 - 5 动生电动势动生电动势的产生可以用洛伦兹力来解释。

长为l 的导体棒与导轨构成矩形回路abcd 平放在纸面内，均匀磁场B 垂直纸面向里。

当导体棒ab 以速度v 沿导轨向右滑动时，导体棒内自由电子也以速度v 随之一起向右运动。

每个自由电子受到的洛伦兹力为B v F ⨯-)(=e ,方向从b 指向a ，在其作用下自由电子向下运动。

如果导轨是导体，在回路中将形成沿着abcd 逆时针方向的电流。

如果导轨是绝缘体，则洛伦兹力将使自由电子在a 端累积，从而使a 端带负电，b 端带正电，在ab 棒上产生自上而下的静电场。

当作用在自由电子上的静电力与洛伦兹力大小相等时达到平衡，ab 间电压达到稳定值，b 端电势比a 端高。

这一段运动导体相当于一个电源，它的非静电力就是洛伦兹力。

电动势定义为单位正电荷从负极通过电源内部移到正极的过程中，非静电力K 所作的功，即B v F K ⨯=-=e.动生电动势为ε⎰⎰+-⋅⨯=⋅=l B v l K d )(d ba .(6.4)均匀磁场情况：若v ⊥ B , 则有ε = B l v ；若导体顺着磁场方向运动，v // B ，则有 v ⨯ B = 0，没有动生电动势产生。

因此，可以形象地说，只有当导线切割磁感应线而运动时，才产生动生电动势。

普遍情况：在任意的恒定磁场中，一个任意形状的导线线圈L (闭合的或不闭合的)在运动或发生形变时，各个线元d l 的速度v 的大小和方向都可能是不同的。

这时，在整个线圈L 中产生的动生电动势为ε l B v d )()(⋅⨯=⎰L .(6.5)图6 - 6 洛伦兹力不作功洛伦兹力对电荷不作功：洛伦兹力总是垂直于电荷的运动速度，即v ⊥F v ，因此洛伦兹力对电荷不作功。

动生电动势和感生电动势§6-2动生电动势和感生电动势动生电动势：回路或其一部分在磁场中的相对运动所产生的感应电动势。

感生电动势：仅由磁场的变化而产生的感应电动势。

一动生电动势图6-5动生电动势动生电动势的产生可以用洛伦兹力来解释。

长为l的导体棒与导轨构成矩形回路abcd平放在纸面内，均匀磁场b垂直纸面向里。

当导体棒ab以速度v沿导轨向右滑动时，导体棒内自由电子也以速度v随之一起向右运动。

每个自由电子受到的洛伦兹力为f=（。

e）v。

b，方向从b指向a，在其作用下自由电子向下运动。

如果导轨是导体，在回路中将形成沿着abcd逆时针方向的电流。

如果导轨是绝缘体，则洛伦兹力将使自由电子在a端累积，从而使a端带负电，b端带正电，在ab棒上产生自上而下的静电场。

当作用在自由电子上的静电力与洛伦兹力大小相等时达到平衡，ab间电压达到稳定值，b端电势比a端高。

这一段运动导体相当于一个电源，它的非静电力就是洛伦兹力。

电动势定义为单位正电荷从负极通过电源内部移到正极的过程中，非静电力k所作的功，即k。

f。

e。

v。

b.动生电动势为。

k。

dl。

a（v。

b）。

dl.b（6.4）均匀磁场情况。

若v。

b，则有。

=blv；若导体顺着磁场方向运动，v。

b，则有v。

b=0，没有动生电动势产生。

因此，可以形象地说，只有当导线切割磁感应线而运动时，才产生动生电动势。

普遍情况：在任意的恒定磁场中，一个任意形状的导线线圈l（闭合的或不闭合的）1在运动或发生形变时，各个线元dl的速度v的大小和方向都可能是不同的。

这时，在整个线圈l中产生的动生电动势为。

（v。

b）。

dl.（l）（6.5）图6-6洛伦兹力不作功洛伦兹力对电荷不作功。

洛伦兹力总是垂直于电荷的运动速度，即fv。

v，因此洛伦兹力对电荷不作功。

然而，当导体棒与导轨构成回路时会有感应电流出现，这时感应电动势却是要作功的。

感应电动势作功能量的来源。

在运动导体中的自由电子不但具有导体本身的运动速度v，而且还具有相对于导体的定向运动速度u，与此相应的洛伦兹力fu。

读《感生电动势与动生电动势的相对性》、《动生电动势还是感生电动势》及《论感生电动势和动生电动势的统一》有感土木一班陈文伟1004010133 学完电磁学，让我对电与磁的本质有了进一步的体会，这与高中学到的完全不在同一个层次上，其中让我感慨最多的是动生电动势与感生电动势。

感生电动势：“导体回路在磁场中无运动，由于磁场的变化而引起B通量变化，这时产生的感应电动势称为感生电动势。

”而动生电动势：“磁场保持不变，由于导体回路或导体在磁场中运动而引起B通量的变化，这时产生的感应电动势称为动生电动势。

”于是对于两种电动势的区别，我们可以理解为，由感生电场产生的电动势是感生电动势，因导体运动而与洛伦兹力有关的电动势是动生电动势。

在看了《感生电动势与动生电动势的相对性》这篇文章之后，我了解二者是相对的，同样是感应电动势，在一种参考系中是动生电动势，在另一个参考系中可能就是感生电动势。

同一物理过程在不同参考系中结论是不一样的，我们可以运用相对论把两种不同的描述统一起来，这篇文章即通过坐标变换在一定程度上消除了动生电动势与感生电动势的界限，即通过坐标变换，它们是可以转换的，但一般不可能完全转换。

于是就有了感生电动势与动生电动势的异同。

不同点：动生电动势：磁场不随时间变化而导体回路的整体或局部运动所产生的感应电动势；感生电动势：导体所围回路面积不变而磁场随时间变化所产生的感应电动势。

相对性：在电磁学中把感应电动势分为动生和感生两种形式，这在一定的程度上只有相对意义。

例如，在某些情况下，可能通过参照系的选取，将感生电动势视为动生电动势。

然而，坐标变换只能在一定程度上消除动生与感生的界限。

在普遍情况下，不可能通过坐标变换，把感生电动势完全归结为动生电动势，反之亦然。

相对论认为，涡旋电场和磁场是统一的，是在不同参照系下观察同一电磁场的结果。

在关联于磁场的参照系看来，运动电荷受到了洛伦兹力——磁场力，而在关联于运动电荷的参照系看来，运动磁场感生了一个电场，静止电荷受到了一个感生电场的电场力。