1-3单纯形法原理

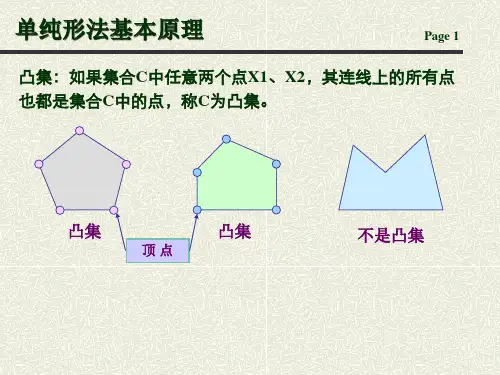
单纯形法的基本原理单纯形法是一种用于求解线性规划问题的数学方法，它的基本原理是通过不断地移动解空间中的顶点来逼近最优解。

在解决实际问题中，我们经常会遇到一些资源有限，而需要在这些资源限制下最大化或最小化某个指标的情况，这时就需要用到线性规划问题。

而单纯形法正是针对这类问题提出的一种高效的求解方法。

单纯形法的基本原理可以用几个关键步骤来概括。

首先，我们需要将线性规划问题转化为标准型，即目标函数为最大化，约束条件为等式的形式。

接着，我们需要找到一个初始可行解，这个可行解需要满足所有的约束条件。

然后，我们通过一系列的基本变量的替换，不断地移动解空间中的顶点，直到找到最优解为止。

在单纯形法中，我们需要利用单纯形表来进行计算。

单纯形表是一个表格，其中包含了目标函数、约束条件、基本变量等信息。

通过对单纯形表的不断变换和计算，我们可以逐步逼近最优解。

在每一步的计算中，我们需要选择一个入基变量和一个出基变量，通过一系列的行变换和列变换来更新单纯形表，直到找到最优解为止。

单纯形法的基本原理虽然看起来比较复杂，但实际上它是建立在一些简单的数学原理之上的。

通过对解空间中的顶点进行移动，我们可以逐步逼近最优解，这是单纯形法能够高效求解线性规划问题的关键所在。

在实际应用中，单纯形法已经被证明是一种非常有效的方法，它可以帮助我们在资源有限的情况下做出最优的决策。

总的来说，单纯形法是一种用于求解线性规划问题的高效方法，它的基本原理是通过不断地移动解空间中的顶点来逼近最优解。

通过对单纯形表的计算和变换，我们可以逐步找到最优解。

在实际应用中，单纯形法已经被广泛地应用于各个领域，它为我们解决资源有限的最优化问题提供了一个强大的工具。

希望本文对单纯形法的基本原理有所帮助，谢谢阅读！。

单纯形法原理及例题
单纯形法原理：
单纯形法是求解线性规划问题的一种数学方法，它是由美国数学家卢克·单纯形于1947年发明的。

用单纯形法求解线性规划的过程，往往利用线性规划的对偶形式，将原问题变换为无约束极大化问题，逐步把极大化问题转换为标准型问题，最后利用单纯形法的搜索方法求解满足所有约束条件的最优解。

例题：
问题：求解最小化目标函数z=2x1+x2的线性规划问题，约束条件如下：
x1+2x2≥3
3x1+x2≥6
x1,x2≥0
解：将上述线性规划问题转换为无约束极大化问题，可得：
极大化问题：
Max z=-2x1-x2
s.t. x1+2x2≤3
3x1+x2≤6
x1,x2≥0
将极大化问题转换为标准型问题，可得：
Max z=-2x1-x2
s.t. x1+2x2+s1=3
3x1+x2+s2=6
x1,x2,s1,s2≥0
运用单纯形法的搜索方法求解：
令x1=0,x2=0，则可得s1=3,s2=6，即(0,0,3,6)是单纯形的初始解；
令z=-2x1-x2=0，代入约束条件，可得x1=3,x2=3，则可得s1=0,s2=0，即(3,3,0,0)是新的单纯形解。

由于s1=s2=0，说明x1=3,x2=3是线性规划问题的最优解，且最小值为z=2*3+3=9。

单纯形法1. 什么是单纯形法单纯形法（Simplex Method）是一种数学优化方法，用于在线性规划问题中寻找最优解。

其基本思想是通过不断地在可行解空间中移动，逐步优化目标函数的值，直到找到最优解。

单纯形法是由美国数学家乔治·达内策在20世纪40年代开发的，成为线性规划问题求解的一种经典方法。

2. 单纯形法的基本原理单纯形法的基本原理是通过构造一系列的顶点组合，这些顶点组合构成了可行解空间的一个多面体，称为单纯形。

每次移动都是在单纯形的边界上进行，直到找到最优解。

2.1 线性规划问题的标准形式在使用单纯形法求解线性规划问题之前，首先需要将问题转化为标准形式。

线性规划问题的标准形式包括以下特征：•最大化目标函数或最小化目标函数•约束条件为等式或不等式•决策变量为非负数2.2 单纯形法的步骤单纯形法的求解步骤如下：1.初始化：将线性规划问题转化为标准形式，并找到初始可行解。

2.检验最优性：计算当前基可行解对应的目标函数值，判断是否达到最优解。

3.寻找进入变量：通过计算目标函数的系数与约束条件中的系数之比，找到使目标函数值最大（或最小）增长的变量。

4.寻找离开变量：从进入变量所属列中选择合适的变量离开基，使得新的基可行解依然满足约束条件。

5.更新基：将进入变量换入基，将离开变量换出基，得到新的基可行解。

6.重复步骤 2-5，直到找到最优解或判断无界。

2.3 单纯形表在单纯形法的求解过程中，通过使用单纯形表（Simplex Table）来记录每一步的计算结果和变量的取值。

单纯形表是一个矩阵，包含基变量、非基变量、目标函数系数、约束条件左边的系数等信息，方便进行计算和调整。

3. 单纯形法的优缺点3.1 优点•单纯形法是一种简单直观的求解线性规划问题的方法，容易理解和实现。

•单纯形法对于规模较小的问题，可以得到精确的最优解。

•单纯形法可以处理带有不等式约束的问题，适用范围广。

3.2 缺点•单纯形法在解决大规模问题时，计算复杂度较高，效率较低。

单纯形法原理解释嘿，朋友！今天咱来聊聊单纯形法，这可是个有点意思的东西。

你想想啊，生活中咱们经常要做各种选择，怎么才能选到最好的那个呢？比如说，去超市买水果，是选苹果还是香蕉，要考虑价格、口感、营养，这其实就有点像单纯形法要解决的问题。

单纯形法呢，简单说就是在一堆限制条件下，找到让某个目标达到最优的办法。

比如说一家工厂生产不同的产品，有材料限制、时间限制，那怎么安排生产能赚最多的钱？这时候单纯形法就派上用场啦！它就像一个聪明的小管家，在复杂的条件里穿梭，帮咱们找出最好的方案。

咱先来说说单纯形法里的那些个“家伙”。

有目标函数，这就好比是咱们的最终目的地，是咱们想要达到的那个最好的结果。

还有约束条件，这就像是路上的各种障碍和规矩，不能随便乱闯。

那单纯形法是怎么工作的呢？它会从一个可行解开始，就像咱们出门先迈出第一步。

然后呢，沿着一定的方向去找更好的解。

这就好比在迷宫里找出口，不断试探，不断前进。

比如说，有个数学问题是这样的：要生产两种产品，A 和 B，生产A 一个需要 2 小时人工和 3 个材料，生产 B 一个需要 3 小时人工和 2个材料，总共有人工 100 小时，材料 120 个，A 产品一个能赚 5 元，B 产品一个能赚 8 元，那怎么生产能赚最多钱？单纯形法就会先找一个能生产的方案，比如说先生产 20 个 A 和 20 个 B。

然后看看，如果多生产一个 A 或者 B，会不会赚更多钱。

如果会，那就调整生产方案。

你说这像不像咱们平时找工作，先找一个能做的，然后看看怎么能做得更好，赚更多钱？单纯形法的厉害之处就在于，它能在复杂的情况里，快速地找到那个最优的答案。

而且啊，它还很可靠，只要条件给清楚了，它就能给出准确的结果。

朋友，你说要是咱们在生活中也能有这么个聪明的法子，帮咱们做各种选择，那得多好啊！比如说选房子，考虑价格、位置、面积，是不是也能用类似单纯形法的思路呢？所以说啊，单纯形法虽然听起来有点复杂，但是弄明白了，真的能帮咱们解决好多难题，让咱们的生活更有条理，更能达到咱们想要的那个“最好”！。

单纯形法原理单纯形法是一种用于求解线性规划问题的数学方法，它通过不断地移动可行解，逐步接近最优解。

单纯形法的基本思想是从一个基本可行解出发，通过有限次迭代，逐步向着最优解靠近。

这种方法的优点是能够有效地处理大规模的线性规划问题，并且在实际应用中取得了很好的效果。

单纯形法的原理可以通过以下步骤来进行解释：首先，我们需要将线性规划问题转化为标准形式，即将不等式约束转化为等式约束，并引入松弛变量。

这样，原始的线性规划问题就可以表示为一个矩阵形式Ax=b的形式，其中A是一个m×n的矩阵，x是一个n维向量，b是一个m维向量。

接下来，我们需要找到一个初始的基本可行解。

这个基本可行解对应于一个m×m的单位矩阵Im，以及一个n维的零向量。

我们可以通过将单位矩阵对应的列向量代入原始的线性规划问题中，来求解初始的基本可行解。

然后，我们需要计算出一个非基本变量的非负进入向量。

这个向量对应于目标函数的系数向量与A的转置矩阵的乘积。

通过计算这个进入向量，我们可以确定哪一个非基本变量可以进入基本变量集合，从而使得目标函数值增加。

接着，我们需要计算出一个基本变量的非正离开向量。

这个向量对应于基本变量对应的列向量与A的转置矩阵的乘积。

通过计算这个离开向量，我们可以确定哪一个基本变量可以离开基本变量集合，从而使得目标函数值继续增加。

最后，我们需要进行基本变量与非基本变量的交换，并更新基本可行解。

这个过程可以通过一系列的矩阵运算来实现，从而得到一个新的基本可行解。

然后，我们可以继续重复上述步骤，直到找到最优解为止。

通过上述步骤，我们可以看出单纯形法的原理是通过不断地移动可行解，逐步接近最优解。

这种方法的优点是能够有效地处理大规模的线性规划问题，并且在实际应用中取得了很好的效果。

总之，单纯形法是一种用于求解线性规划问题的有效方法，它的原理是通过不断地移动可行解，逐步接近最优解。

在实际应用中，单纯形法已经取得了很好的效果，能够有效地处理大规模的线性规划问题。

单纯形法的原理(一)单纯形法（Simplex Method）什么是单纯形法单纯形法是一种用于解决线性规划问题的方法。

它通过迭代的方式，逐步接近最优解。

在线性规划中，我们需要在一组线性约束条件下，最大化或最小化一个线性目标函数。

单纯形法是一种基于几何性质的方法，它通过在可行域内移动到较优区域，逐步逼近最优解。

线性规划问题的标准形式在介绍单纯形法之前，我们先来了解一下线性规划问题的标准形式。

线性规划问题可以写成如下形式：最大化目标函数：[Z = c_1x_1 + c_2x_2 + … + c_nx_n]满足约束条件：[a_{11}x_1 + a_{12}x_2 + … + a_{1n}x_n ≤ b_1][a_{21}x_1 + a_{22}x_2 + … + a_{2n}x_n ≤ b_2]…[a_{m1}x_1 + a_{m2}x_2 + … + a_{mn}x_n ≤ b_m]其中，(x_1, x_2, …, x_n) 是决策变量，(c_1, c_2, …, c_n) 是目标函数的系数，(a_{ij}) 是约束条件的系数，(b_i) 是约束条件的右侧常数。

单纯形法的基本思想单纯形法的基本思想是通过在可行域内移动，逐步逼近最优解。

其算法步骤如下：1.初始化阶段：将线性规划问题转化为标准形式，并构造初始的基可行解。

2.优化阶段：根据当前的基可行解，计算出相应的目标函数值。

3.检验最优解：如果当前的基可行解是最优解，则停止算法；否则，继续下一步。

4.确定进入和离开变量：根据当前基可行解，确定进入变量和离开变量。

5.计算新的基可行解：通过计算和替换，得到新的基可行解。

6.回到步骤2：不断迭代，直到获得最优解。

单纯形法的关键概念在单纯形法中，有几个关键概念需要了解：1.基变量（Basic Variables）：在线性规划问题中，基变量是指与基矩阵中的列相对应的决策变量。

基变量的值通过基可行解来确定。

2.非基变量（Nonbasic Variables）：非基变量是指未在基可行解中出现的决策变量。

单纯形法原理
单纯形法是一种用于求解线性规划问题的经典方法。

它基于一个重要的原理，即通过不断地改变可行解来寻找最优解。

首先，我们需要将线性规划问题转化为标准形式，即目标函数最小化的约束条件下的线性等式约束问题。

然后，我们引入一组基变量，用它们来表示约束条件中的不等式。

这样，我们就可以将问题表示为一个矩阵方程。

通过逐步迭代的过程，单纯形法从初始可行解开始，在每一步中选择合适的基变量进入基组合，同时选择一个离开基变量离开基组合。

这个选择过程基于目标函数的增益最大化。

在每一步中，我们计算一个指标称为换入变量的相对利润。

然后，我们选择具有最大相对利润的变量作为新的基变量。

接下来，我们计算每个基变量的换出变量，以确定哪个变量将离开基组合。

换出变量的选择基于非基变量进入基变量的限制条件。

通过不断地魔法步骤，我们可以逐渐靠近最优解。

当达到最优解时，指标函数的值为最小值，而最终的基变量和非基变量的值则保存了最优解的解。

需要注意的是，单纯形法并不总是在有限时间内结束。

在某些情况下，它可能会进入一个无穷循环，无法找到最优解。

为了解决这个问题，我们可以添加一些人工变量，并进行二阶段法来确保最优解的存在。

总之，单纯形法是一种有效的线性规划求解方法，它通过不断改变可行解来寻找最优解。

通过选择合适的基变量和换出变量，单纯形法能够逐步逼近最优解。

单纯形算法原理与计算步骤详解单纯形算法是一种常用于线性规划问题求解的优化算法，其基本思想是通过不断迭代改变可行解，使目标函数值逐渐趋近最优解。

本文将详细介绍单纯形算法的原理和计算步骤。

一、单纯形算法原理单纯形算法基于以下原理：假设存在一个线性规划问题，其中目标函数需要最小化，约束条件为一组线性等式和不等式。

算法通过在可行域内循环改变基变量，以求得最优解。

算法的基本思想是从初始可行解出发，不断迭代地转移到更优的解，直到找到最优解。

单纯形算法的迭代过程中，每一次迭代都会选择一个非基变量进行转移，使目标函数值逐步减小。

二、单纯形算法的计算步骤下面将详细介绍单纯形算法的计算步骤，以帮助读者更好地理解该算法。

1. 初始化阶段在初始化阶段，需要将线性规划问题转化为标准型，并找到初始可行解。

标准型的要求是：目标函数为最小化，约束条件为等式和非负约束。

2. 检验阶段在检验阶段，需要进行基变量的选择和检验是否达到最优解。

首先选择一个入基变量，该变量的选择通常基于某些准则，如最大增量准则、最小比率准则等。

3. 转换阶段在转换阶段，需要进行基变量的转换，使目标函数值不断减小。

通过将选定的入基变量与已有的基变量组成一个新的基，进而得到新的可行解。

在转换过程中，还需要进行非基变量的选择和计算。

选择一个出基变量，使得目标函数值减小的幅度最大。

然后，通过高斯消元法计算出相应的新基。

4. 终止判断阶段在每次迭代后，都需要判断是否已达到最优解或存在无界解。

如果目标函数不能减小或者无界，则算法终止。

否则，返回检验阶段继续迭代。

5. 结果输出阶段当算法终止时，需要输出最优解以及最优解对应的目标函数值。

三、单纯形算法的优化尽管单纯形算法是一种常用的线性规划求解方法，但在某些情况下，其迭代次数可能会非常大。

为了优化算法效率，可以采用以下方法：1. 人工变量法当初始可行解需要引入人工变量时，可以通过人工变量法来优化算法。

该方法通过对目标函数引入人工变量，并对目标函数进行最小化，从而减少迭代次数。