固体物理基础解答吴代鸣
- 格式:docx
- 大小:197.70 KB
- 文档页数:10


固体物理书籍推荐固体物理作为物理专业的一门基础课程,对以后从事物理科研有着重要的意义。
根据我的了解,给大家推荐一些书。
中文书籍:1、黄昆原著韩汝琦改编,《固体物理学》,高等教育出版社,1988.2、阎守胜著,《固体物理基础》(第二版),北京大学出版社,2003.3、陆栋、蒋平、徐至中著,《固体物理学》,上海科学技术出版社,2003.另外中文书籍还有:谢希德、方俊鑫著,《固体物理学》,上海科学技术出版社,1961方俊鑫、陆栋著,《固体物理学》(上下册),上海科学技术出版社,1980.蒋平、徐至中著,《固体物理简明教程》(第二版),复旦大学出版社,2007.顾秉林、王喜坤著,《固体物理学》,清华大学出版社,1989徐毓龙、阎西林著,《固体物理》,西安电子科技大学出版社,1990朱建国、郑文琛、郑家贵、孙小松、王洪涛著,《固体物理学》,高等教育出版社,2005陈长乐著,《固体物理学》(第二版),高等教育出版社,2007王矜奉著,《固体物理教程》(第三版),山东大学.2003.吴代鸣著,《固体物理习题详解》,吉林人民出版社,1983.黄波、聂承昌著《固体物理学问题和习题》,国防工业出版社,1988.徐至中著,《固体物理学习题解答》,上海科学技术文献出版社,1989.王矜奉著,《固体物理概念题和习题指导》,山东大学.2001.张永德主编,《固体物理及物理量测量》(物理学大题典⑦) ,科学出版社,2005. 英文书籍1、Charles Kittel ,《Introduction to Solid State Physics》(8th Ed),John Wiley and Sons, Inc., 2004.2、Neil W.Ashcroft and N David Mermin, 《Solid State Physics》,Holt Rinehart & Winston,1976.3、G. Grosso and G. P. Parravicini ,《Solid state physics 》,Academic Press ,2000.4、J. R. Hook and H. E. Hall,《Solid State Physics》(2nd,Ed), Wiley,1995.英文书籍还有:Philip Phillips,《Advanced Solid State Physics》,Westview Press,2002.S Doniach and EH Sondheimer,《Green's functions for solid state physicists》,Imperial College Press,1998.Max Wagner,《Unitary transformations in solid state physics》,Elsevier Science Ltd,1986Yuri M. Galperin,《Introduction to Modern Solid State Physics》,lecture note。

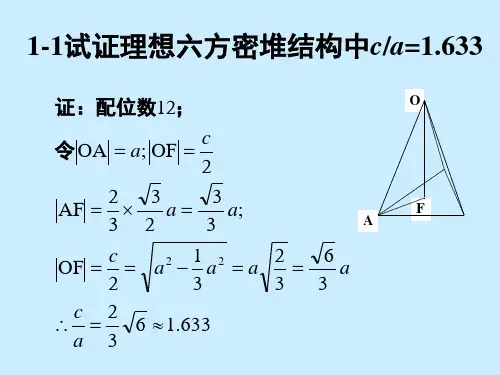
固体物理基础答案解析吴代鸣1.试证理想六方密堆结构中c/a=1.633.证明:如图所示,六方密堆结构的两个晶格常数为a 和c 。
右边为底面的俯视图。
而三个正三角形构成的立体结构,其高度为2.若晶胞基矢c b a,,互相垂直,试求晶面族(hkl )的面间距。
解:c b a ,,互相垂直,可令k c c j b b i a a===,,晶胞体积abc c b a v =⨯⋅=)(倒格子基矢: kcj b i a abc b a v b j b i a k c abc a c v b ia k c jb abc c b v b πππππππππ2)(2)(22)(2)(22)(2)(2321=⨯=⨯==⨯=⨯==⨯=⨯=而与 (hkl )晶面族垂直的倒格矢222321)()()(2)(2cl b k a h G k c l j b k i a h b l b k b h G ++=∴++=++=ππ故(hkl ) 晶面族的面间距222222)()()(1)()()(222cl b k a h cl b k a h G d ++=++==πππ3.若在体心立方晶胞的每个面中心处加一个同类原子,试说明这种晶体的原胞应如何选择?每个原胞含有几个原子? 答:通过分析我们知道,原胞可选为简单立方,每个原胞中含有5个原子。
体心,八个顶点中取一个,对面面心各取一个原子(即三个)作为基元。
布拉菲晶格是简单立方格子。
4.试求面心立方结构的(111)和(110)面的原子面密度。
解:(111)面平均每个(111)面有2213613=⨯+⨯个原子。
(111)面面积()222232322)22()2(221a a a a a a =⋅=-⋅ 所以原子面密度22)111(34232aa ==σ(110)面平均每个(110)面有2212414=⨯+⨯个原子。
(110)面面积222a a a =⋅所以(110)面原子面密度22)110(222aa==σ5.设二维矩形格子的基矢为j a a i a a2,21==,试画出第一、二、三、布里渊区。


1.试证理想六方密堆结构中c/a=1.633. 证明:如图所示,六方密堆结构的两个晶格常数为a 和c 。
右边为底面的俯视图。
而三个正三角形构成的立体结构,其高度为2.若晶胞基矢c b a,,互相垂直,试求晶面族(hkl )的面间距。
解:c b a ,,互相垂直,可令k c c j b b i a a===,,晶胞体积abc c b a v =⨯⋅=)(倒格子基矢:kcj b i a abc b a v b j b i a k c abc a c v b ia k c jb abc c b v bπππππππππ2)(2)(22)(2)(22)(2)(2321=⨯=⨯==⨯=⨯==⨯=⨯=而与 (hkl )晶面族垂直的倒格矢222321)()()(2)(2cl b k a h G k c l j b k i a h b l b k b h G ++=∴++=++=ππ 故(hkl ) 晶面族的面间距222222)()()(1)()()(222cl b k a h cl b k a h G d ++=++==πππ3.若在体心立方晶胞的每个面中心处加一个同类原子,试说明这种晶体的原胞应如何选择?每个原胞含有几个原子? 答:通过分析我们知道,原胞可选为简单立方,每个原胞中含有5个原子。
体心,八个顶点中取一个,对面面心各取一个原子(即三个)作为基元。
布拉菲晶格是简单立方格子。
4.试求面心立方结构的(111)和(110)面的原子面密度。
解:(111)面平均每个(111)面有2213613=⨯+⨯个原子。
(111)面面积()222232322)22()2(221a a a a a a =⋅=-⋅ 所以原子面密度22)111(34232aa ==σ(110)面平均每个(110)面有2212414=⨯+⨯个原子。
(110)面面积222a a a =⋅所以(110)面原子面密度22)110(222a a==σ5.设二维矩形格子的基矢为j a a i a a2,21==,试画出第一、二、三、布里渊区。


固体物理基础(吴代鸣之高教版)课后1到10题答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN一. 本章习题P272习题1.试证理想六方密堆结构中c/a=1.633.一. 说明:C 是上下底面距离,a 是六边形边长。
二. 分析:首先看是怎样密堆的。
如图(书图1.10(a),P8),六方密堆结构每个格点有12个近邻。
(同一面上有6个,上下各有3个)上下底面中间各有一个球,共有六个球与之相切,每个球直径为a 。
中间层的三个球相切,又分别与上下底面的各七个球相切。
球心之间距离为a 。
所以球心之间即格点之间距离均为a (不管是同层还是上下层之间)。
三.证明:如图OA=a ,OO ’=C/2(中间层是上下面层的一半),AB=a O ’是ΔABC 的三垂线交点33'aAB AO ==∴(由余弦定理)330cos 2,30cos 230cos 2222a a x x a ax x a x ===-+=633.1322384132)2()2()3()2(2222222222''≈===∴+=+=+=a c c a ac a ac OA AO OO2.若晶胞基矢c b a,,互相垂直,试求晶面族(hkl )的面间距。
一、分析:我们想到倒格矢与面间距的关系G d π2=。
倒格矢与晶面族 (hkl )的关系321b l b k b h G++=写出)(321b b b 与正格子基矢 )(c b a的关系。
即可得与晶面族(hkl ) 垂直的倒格矢G。
进而求得此面间距d 。
二、解:c b a ,,互相垂直,可令k c c j b b i a a===,,晶胞体积abc c b a v =⨯⋅=)(倒格子基矢: kcj b i a abc b a v b j b i a k c abc a c v b ia k c jb abc c b v b πππππππππ2)(2)(22)(2)(22)(2)(2321=⨯=⨯==⨯=⨯==⨯=⨯=而与 (hkl )晶面族垂直的倒格矢 222321)()()(2)(2cl b k a h G k cl j b k i a h b l b k b h G ++=∴++=++=ππ故(hkl ) 晶面族的面间距222222)()()(1)()()(222cl b k a h cl b k a h Gd ++=++==πππ3.若在体心立方晶胞的每个面中心处加一个同类原子,试说明这种晶体的原胞应如何选择每个原胞含有几个原子1.分析:考虑选取原胞的条件:(即布拉菲晶格的最小单元)(1)体积最小的重复结构单元(2)只包含一个格点(3)能反映晶格的周期性应将几个原子组合成一个格点,然后构成原胞。

本科及研究⽣物理专业书、讲义研究⽣nolting多体物理前两章+bernvig拓扑绝缘体第2章、第4章+kai sun ⾼等凝聚态物理讲义(此讲义中拓扑绝缘体讲得⾮常易懂,会讲清楚基础知识,学完会打下很好的基础,和nolting书⼀样,不跳步骤,⼀步⼀步推导,但⽐noting书讲得更多,⽐如讲义中的紧束缚模型,直接讲到能和科研衔接。
kai sun的主页还有他教的其他课程的讲义,⽐如⼆次量⼦化、重整化群、费⽶液体理论、⾼等量⼦⼒学这些。
)学⼀门课必须同时看两本书,⼀本中⽂书,⼀本英⽂书,才能学好——物理学家特别是读研时。
⽽且有看不懂的地⽅时,还应查其他书。
从量⼦⼒学开始就不能只看⼀本物理书,学⼀门课应同时看⼏本书固体物理:河北师范书+北⼤书(北⼤书虽然有的内容写得不好,但是有的内容写得⾮常好,经典,⽐如固体热容、近⾃由电⼦近似、紧束缚近似77、78页,北⼤书应该和别的书⼀起看)1.《固体物理基础(第⼆版)》吴代鸣:据说这本书很好懂,但是讲解⽐较基础,但不是很深⼊,因为它说尽量避免繁琐的数学推导。
不推荐这本书,因为不是很全⾯。
2.《固体物理基础》孙会元(这本书有些内容有错误):也是和阎守胜、《solid state physics》的编排⼀样,从⾦属⾃由电⼦论讲起。
这本书⽐阎守胜的写的好。
这本书第⼀章⾦属⾃由电⼦论讲得很好,这⼀章虽然有很少的缺点(没有解释清楚费⽶⾯附近的电⼦速度都是近似取和电场⽅向相反的费⽶速度。
第⼆章晶体结构也写得很好,条理很清楚,就像华中师⼤汪德新的《量⼦⼒学》⼀样。
但是第三章能带论开始就写的不是很好了,有些地⽅看不懂。
这本书有些部分写得很好,有些写得不是很好懂(但这种情况⽐较少),所以这书还是⼀本很值得读的固体物理书。
我发现这本固体物理书中德哈斯范阿尔芬效应部分的推导和⽅俊鑫的书中的推导和⽂字⼀样,也就是说孙会元抄袭了⽅俊鑫的书,感觉这样有⼀些不好。
3.胡安的固体物理中就倒格⼦那⼀节写得很好,倒格⼦的性质归纳得很好,特别是把傅⾥叶变换这个性质证明得⾮常好。

11.设有一维单原子晶格,在简谐近似下,考虑每一原子与其余所有原子的作用,试求格波的色散关系。
解:第n 个原子位移x n ,第n+p 个位移x n+p ,第n-p 个位移x n-p (P=1,2,3,……)。
设最近邻原子间力常数为β1,次近邻β2,再次近邻β3,……βp简谐近似下(由书P47,式3.1.6):∑≠+=ji ij ij x U U 2041β第n个原子的运动方程:)(22n i in n i n nx x x U dtx d M -=∂∂-=∑≠β第n+p 和第n-p 个原子对第n 个原子的作用力:)2()()(n p n p n p p n n p n p n p p x x x x x x x f -+=---=-+-+βββ第n 个原子总的受力:)2(n p n p n p pp px x x f -+=-+∑∑β运动方程:)2(22n p n p n p pnx x x dt x d M -+=-+∑β试探解:)(t naq i n Ae x ω-= 代入运动方程:)2cos 2(0)2(22-=-∴≠-+=-∑∑-paq M x x e x e x Mx p pn n ipaq n ipaq n p pn βωβω所以色散关系为:)cos 1(2)(2pqa Mq pp-=∑βω12. 设有一维双原子晶格,最近邻原子间的力常数交错地等于β和10β,假定两种原子的质量相等,最近邻原子间距为a/2,试求格波的色散关系。
解:同一维单原子类似,可写出两种原子的运动方程n n n n u v v dt u d M βββ21010122-+=- n n n nv u u dtv d M βββ102122⨯-+=+ 试探解为)(t naq i n Ae u ω-= )(t naq i n Be v ω-=代入运动方程有:n n iaq n n u v e v Mu βββω210102-+=-- n iaq n n n v e u u Mv βββω202-+=-将u n 、v n 代入消去公因子)(t naq i e ω-得BA e AB M A B B e A M iaqiaq βββωβββω202101022-+=--+=--整理,化为关于A 、B 的线性方程组{)20()1(0)1(10)2(22=-++-=+---B M A e B e A M iaqiaq ωβββωβA ,B 有非零解的条件是上式系数行列式等于零,即2220)1()1(102ωβββωβM e e M iaqiaq -+-+---0=有)cos 1(210202400)1)(1(10)20)(2(24222222=+⋅-+--∴=++⋅----aq M M M e e M M iaq iaq βωωβωββββωβωβ即0)cos 1(20222422=-++-qa M M βωωβ 解出:{}2122222)]cos 1(204)22[(2221)(qa M M M M q -⋅-±=βββω])cos 20101(11[21qa M+±=β13.求出一维单原子晶格的模密度,并导出在低温下晶格比热与温度关系。

一.本章习题P272习题1、试证理想六方密堆结构中c/a=1、633、一. 说明:C 就是上下底面距离,a 就是六边形边长。
二. 分析:首先瞧就是怎样密堆的。
如图(书图1、10(a),P8),六方密堆结构每个格点有12个近邻。
(同一面上有6个,上下各有3个)上下底面中间各有一个球,共有六个球与之相切,每个球直径为a 。
中间层的三个球相切,又分别与上下底面的各七个球相切。
球心之间距离为a 。
所以球心之间即格点之间距离均为a(不管就是同层还就是上下层之间)。
三. 证明:如图OA=a,OO ’=C/2(中间层就是上下面层的一半),AB=a O ’就是ΔABC 的三垂线交点33'a AB AO ==∴(由余弦定理)330cos 2,30cos 230cos 2222a a x x a ax x a x ===-+=633.1322384132)2()2()3()2(2222222222''≈===∴+=+=+=a c c a ac a ac OA AO OO2.若晶胞基矢c b a,,互相垂直,试求晶面族(hkl)的面间距。
一、分析:我们想到倒格矢与面间距的关系G d π2=。
倒格矢与晶面族 (hkl)的关系321b l b k b h G++=写出)(321b b b 与正格子基矢 )(c b a的关系。
即可得与晶面族(hkl) 垂直的倒格矢G 。
进而求得此面间距d 。
二、解:c b a ,,互相垂直,可令k c c j b b i a a===,,晶胞体积abc c b a v =⨯⋅=)(倒格子基矢:kcj b i a abc b a v b j b i a k c abc a c v b ia k c jb abc c b v b πππππππππ2)(2)(22)(2)(22)(2)(2321=⨯=⨯==⨯=⨯==⨯=⨯=而与 (hkl)晶面族垂直的倒格矢 222321)()()(2)(2cl b k a h G k cl j b k i a h b l b k b h G ++=∴++=++=ππ故(hkl) 晶面族的面间距222222)()()(1)()()(222cl b k a h cl b k a h G d ++=++==πππ3.若在体心立方晶胞的每个面中心处加一个同类原子,试说明这种晶体的原胞应如何选择?每个原胞含有几个原子?1.分析:考虑选取原胞的条件:(即布拉菲晶格的最小单元)(1)体积最小的重复结构单元(2)只包含一个格点(3)能反映晶格的周期性应将几个原子组合成一个格点,然后构成原胞。
8.证明一维NaCl 晶格的Madelung 常数2ln 2α=。
证明:任选一个离子为参考离子i ,左右两侧对称分布,令ij j r a a =(a 为晶格常数) 则有:111112......1234jj aα⎡⎤±=-+-+⎢⎥⎣⎦∑=同号为-,异号为+。
已知级数234l n (1)......234x x x x x +=-+-+令x=1 则得:111l n 21......234=-+-+ 故Madelung 常数2ln 2α=。
9.若离子间的排斥势用-r/eρλ来表示,只考虑最近邻离子间的排斥作用,试导出离子晶体结合能的表达式,并讨论参数λ和ρ应如何决定。
解:设最近邻离子间距离为r ,则ij j r a r =(以离子i 为原点)2/0204()4ij r ij ijij ij e e r r r u r e r ρλπεπε-⎧-=⎪⎪=⎨⎪±⎪⎩,(最近邻,),(最近邻以外)总的相互作用能为:2/()0124Nr j i j Ne U e ra ρλπε-≠⎡⎤=-±-⎢⎥⎢⎥⎣⎦∑∑最近邻 2/0..........................(1)24r Ne U Z e r ραλπε-⎡⎤∴=-+⎢⎥⎣⎦; 其中Z 为最近邻离子数 由平衡条件00r r U r =∂⎛⎫= ⎪∂⎝⎭得02/200.........................(2)4r e Z e r ρραλπε-= 得20001.......................(3)24N e U r r αρπε⎡⎤=-⎢⎥⎣⎦ 结合能0()c E U r =- 对于NaCl 等离子晶体:02201...................(4)9r rU K Nr r =⎛⎫∂= ⎪∂⎝⎭02/32000121............(5)184r e Z K e r r ραλπερ-⎡⎤-∴=+⎢⎥⎣⎦将(2)代入(5)得: 22320000121..................(6)1844e e K r r r ααπεπερ⎡⎤=-+⋅⎢⎥⎣⎦202400.........................(7)272e r e r K αραπε∴=+ 由(2)得:02/200......................(8)4r e e r Zρραλπε=则4220002003611243r K e e U r e πεααπεα⎛⎫⎛⎫-=-- ⎪⎪⎝⎭⎝⎭10.如果NaCl 晶体中离子的电荷增加一倍,假定排斥势不变,试估计晶体的结合能以及离子间的平衡距离将产生多大变化?解:总相互作用能20........(1)24n N e B U r r απε⎛⎫=--⎪⎝⎭ 02210000...........(2)24n r r U N e nB r r r απε+=⎛⎫∂⎛⎫=-= ⎪ ⎪∂⎝⎭⎝⎭得到:11'0024..............(2)n nB r e πεα-⎛⎫=⎪⎝⎭由(2)得到:2100...............(3)4n e B r nαπε-=将(3)代入(1)得: 20001()1........(4)8N e U r r n απε⎛⎫=-- ⎪⎝⎭当电荷由e 变为2e 时,由(2·)和(4)可得:1010(2)4()n r e r e -= 1(2)4()nn U e U e -= 11.在一维单原子晶格中,若考虑每一个原子与其余所有原子都有作用,在简谐近似下求格波的色散关系。
固体物理基础解答吴代鸣————————————————————————————————作者: ————————————————————————————————日期:1.试证理想六方密堆结构中c/a =1.633. 证明:如图所示,六方密堆结构的两个晶格常数为a 和c 。
右边为底面的俯视图。
而三个正三角形构成的立体结构,其高度为2.若晶胞基矢c b a,,互相垂直,试求晶面族(hkl )的面间距。
解:c b a ,,互相垂直,可令k c c j b b i a a===,,晶胞体积abc c b a v =⨯⋅=)(倒格子基矢:kcj b i a abc b a v b j b i a k c abc a c v b ia k c jb abc c b v bπππππππππ2)(2)(22)(2)(22)(2)(2321=⨯=⨯==⨯=⨯==⨯=⨯=而与 (h kl )晶面族垂直的倒格矢222321)()()(2)(2cl b k a h G k c l j b k i a h b l b k b h G ++=∴++=++=ππ 故(hkl ) 晶面族的面间距222222)()()(1)()()(222cl b k a h cl b k a h G d ++=++==πππ3.若在体心立方晶胞的每个面中心处加一个同类原子,试说明这种晶体的原胞应如何选择?每个原胞含有几个原子? 答:通过分析我们知道,原胞可选为简单立方,每个原胞中含有5个原子。
体心,八个顶点中取一个,对面面心各取一个原子(即三个)作为基元。
布拉菲晶格是简单立方格子。
4.试求面心立方结构的(111)和(110)面的原子面密度。
解:(111)面平均每个(111)面有2213613=⨯+⨯个原子。
(111)面面积()222232322)22()2(221a a a a a a =⋅=-⋅ 所以原子面密度22)111(34232aa ==σ(110)面平均每个(110)面有2212414=⨯+⨯个原子。
(110)面面积222a a a =⋅所以(110)面原子面密度22)110(222a a==σ 5.设二维矩形格子的基矢为j a a i a a2,21==,试画出第一、二、三、布里渊区。
解:倒格子基矢:jb j a j a j ax x a a a a v b k x a i ax i a x a a a a v b 11323321212212222)(2)(2222)(2===⋅⋅=⨯===⋅⋅=⨯=πππππππ所以倒格子也是二维矩形格子。
2b方向短一半。
最近邻;,22b b-次近邻;2,2,,2211b b b b--再次近邻;,,,12122121b b b b b b b b---+-再再次近邻;3,322b b-做所有这些点与原点间连线的垂直平分线,围成布里渊区。
再按各布里渊区的判断原则进行判断,得:第一布里渊区是一个扁长方形;第二布里渊区是2块梯形和2块三角形组成;第三布里渊区是2对对角三角和4个小三角以及2个等腰梯形组成。
6.六方密堆结构的原胞基矢为:k c a j a i a a ja i a a=+-=+=32123212321试求倒格子基矢并画出第一布里渊区。
解:原胞为简单六方结构。
原胞体积:c a j i j i c a i j ac j i a k c j i a j i a a a a v 2232123)3()3(41)]3(21[)3(21])3(21[)3(21)(=+⋅+=+⋅+=⨯+-⋅+=⨯⋅=倒格子基矢:kca a vb j i aj i a k c c a a a vb j i a kc j i a c a a a v b ππππππππ2)(2)3(2)]3(21[232)(2)3(32])3(21[232)(221321322321=⨯=+-=+⨯=⨯=+=⨯+-=⨯=由此看到,倒格子同原胞一样,只是长度不同,因此倒格子仍是简单六方结构。
(注意:倒格子是简单六方,而不是六方密堆)选六边形面心处格点为原点,则最近邻为六个角顶点,各自倒格矢的垂直平分面构成一个六面柱体。
次近邻为上下底面中心,其垂直平分面为上下平行平面。
再次近邻是上下面六个顶角,其垂直平分面不截上面由最近邻和次近邻垂直平分面构成的六角柱体。
所以第一布里渊区是一个六角柱体。
比倒格子六方要小。
7.略8、证明一维NaCl 晶体的马德隆常数为2ln 2=α证明:,,则左右两侧对称分布任选一参考离子i 最近距离)为晶格常数(正负离子;这里令a a a r j ij =.为其中,异号为+;同号; (4131211121)=那么,有:-⎥⎦⎤⎢⎣⎡+-+-=±∑j ja α (4)32)1ln(利用展开式:432+-+-=+x x x x x (4)1312112ln ,得:1令+-+-==x 2ln 2=∴α9、若离子间的排斥势用ρλre -来表示,只考虑最近邻离子间的排斥作用,试导出离子晶体结合能的表达式,并讨论参数λ和ρ应如何决定。
解:离子为原点)(以,则设最近邻离子间距离为i r a r r j ij =⎪⎪⎩⎪⎪⎨⎧±=-=-,(最近邻以外)4),(最近邻,4)(0202/ij ij ij r ij r e r r r e er u ij πεπελρ⎥⎦⎤⎢⎣⎡-±-=∑∑-≠最近邻/)(02142总相互作用能为:ρλπεr Nij jea re N U为最近邻离子数其中)1......(....................;42/02Z e Z r e NU r ⎥⎦⎤⎢⎣⎡+-=∴-ρλπεα)2.....(....................4;得:0由平衡条件:/20020ρλπεραr r r eZ r e r U -===⎪⎪⎭⎫ ⎝⎛∂∂)3...(....................142得:0002⎥⎦⎤⎢⎣⎡-=r r e NU ρπεα )(结合能0r U E c -=)4.........(. (91)等离子晶体:对于0220r r r U Nr K NaCl =⎪⎪⎭⎫⎝⎛∂∂= )5..(..........142181/2300200⎥⎦⎤⎢⎣⎡+-=∴-ρρλπεαr e Z r e r K )6........(..........1442181得:)5(代入)2(将200230020⎥⎦⎤⎢⎣⎡⋅+-=ρπεαπεαr e r e r K)7.....(.. (7224)00202Kr e r e πεααρ+=∴ )8..(....................4得:)2(由/20020ρπεραλreZr e =10、如果NaCl 结构晶体中离子的电荷增加一倍,假定排斥势不变,试估计晶体的结合能及离子间的平衡距离将产生多大变化。
解:)1........(42总相互作用能02⎪⎪⎭⎫ ⎝⎛--=n r B r e NU πεα )2.(..........0421020020=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛∂∂+=n r r r nB r e N r U πεα )2....(..........4得:'11200-⎪⎪⎭⎫⎝⎛=n e nB r απε)3.....(..........4得:)2(由1002-=n r ne B πεα)4........(118)(得:)1(代入)3(0020⎪⎪⎭⎫ ⎝⎛--=n r e N r U πεα 11100'4)()2(4)()2(可知:)4(和)2(时,由2变为当电荷由--==n nne U e U e r e r e e11、在一维单原子晶格中,若考虑每一院子于其余所有原子都有作用,在简谐近似下求格波的色散关系。
∑∑≠≠+=-=ji ijij j i ij ij u U u x U 20041)(21解:在简谐近似下:βφ)(41个原子的运动方程:第222∑≠∂∂-=∂∂-=j i ij ij n n n u u u U dtu d m n β)(41右边)(2)(2∑∑≠≠+∂∂-=n j nj nj n i in in n u u u ββ))()((41)(2)(2∑∑≠≠-+-∂∂-=n j n j nj n i i n in n u u u u u ββ))()((21)()(∑∑≠≠----=nj n j nj n i i n in u u u u ββ∑≠-=)()(ni n i in u u β∑-+=-+pn p n pn p u u u )2(β∑-+=-=---+------pn aq p n t i aq p n t i pnaq t i naq t i n u Ae Ae Ae m Ae u )2(代入上式得:设))(())(()(2)(ωωωωβω∑-=pppaq m)cos 1(2整理,得:2βω 12、设有一维双原子晶格,两种院子的质量相等,最近邻原子间的力常数交错地等于1β和2β,试求格波的色散关系。
nn n n n n n n u u u dtu d m )()()(解:2121121122ββυβυβυβυβ+-+=-+-=--nn n n n n n n u u u u dt d m υββββυβυβυ)()()(2111211222+-+=-+-=++)()(;试探解:t naq i n t naq i n Be Ae u ωωυ----==BA AeB m A B Be A m iaq iaq )()(代入方程,得:2121221212ββββωββββω+-+=-+-+=--0)()()(2121221221=+-++--+-ββωββββωββm e e m iaq iaqmaqcos 2经计算,得:212221212ββββββω++±+=13、已知一维单原子晶格的格波色散关系为)cos 1(2)(2qa Mq -=βω试求:(1)格波的模密度g(ω);(2)低温下晶格热容与温度的比例关系。
⎰-=))((2)(解:一维时,模密度q dq lg ωωδπωaqdqMad Maq sin 22;21cos 由色散关系,得:2βωωωβ=-=2/142224⎪⎪⎭⎫ ⎝⎛-=∴ωβωββωωM M M a d dq ⎰⎪⎪⎭⎫ ⎝⎛--⋅=m q M q M M a q q d q l g ωωβωββωωδωωπω02/14222)(4)())(()()(22)( 2/142224⎪⎪⎭⎫ ⎝⎛-=ωβωββωπM M Ma l⎰-∂∂=⎪⎪⎭⎫ ⎝⎛∂∂=mT k d g T T EC B ωυυωωωω01)/exp()(晶格热容:)1项,(因为低温,略去4<<ωω⎰-⋅∂∂=∴mB Tk e d M M a l TC ωωυωωωββωπ01 ⎰∞-∂∂=01ωωβπωd eTM alTk B)似为无穷大主要,所以上限可以近因为低温,频率低的占(⎰∞-=0222)1(dx e e x T k M al xxBβπ3经计算,上面积分=2πT Ma lk C B ⋅=∴βπυ3214、将De bye 模型用于一维晶格,求低温下晶格热容与温度的关系,并和上题的结果进行比较,讨论Debye 模型的合理性。