8第八讲(弯曲内力图)分析
- 格式:ppt
- 大小:571.00 KB
- 文档页数:15





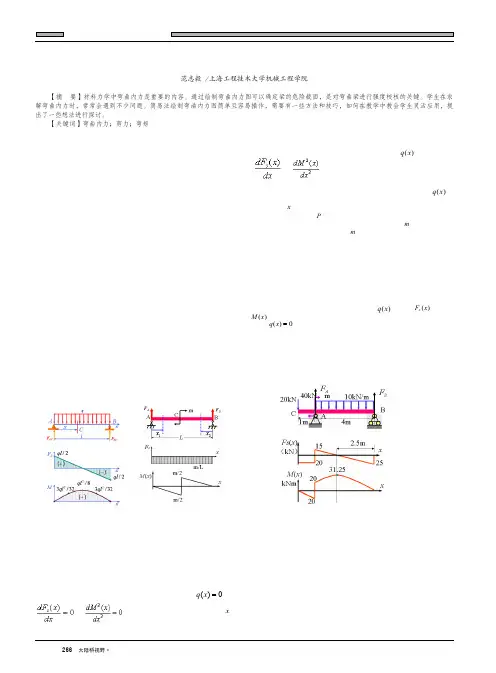
文化教育・Cultural Education 266 大陆桥视野·2016年第20期弯曲内力图教学方法探讨范志毅 / 上海工程技术大学机械工程学院【摘 要】材料力学中弯曲内力是重要的内容。
通过绘制弯曲内力图可以确定梁的危险截面,是对弯曲梁进行强度校核的关键。
学生在求解弯曲内力时,常常会遇到不少问题。
简易法绘制弯曲内力图简单且容易操作,需要有一些方法和技巧,如何在教学中教会学生灵活应用,提出了一些想法进行探讨。
【关键词】弯曲内力;剪力;弯矩一、引言材料力学中求杆件内力,是最基本的内容。
内力的求解主要包含三种:轴向拉压杆轴力、扭转轴的扭矩、弯曲梁的剪力和弯矩。
其中梁的剪力和弯矩的求解较复杂些。
绘制剪力图和弯矩图有两个方法,第一是根据剪力方程和弯矩方程来绘制剪力图和弯矩图;第二是只需求出关键截面的内力,根据总结的规律绘制内力图,也称为简易法。
由于简易法绘制内力图简单,基本上在教学过程中会用较多的课时教授简易法。
熟练掌握简易法,就能快速简便地绘制内力图,但教学的过程中不少学生还是不能很好地掌握。
通过教学中不断总结经验,对简易法的教学提出了一些想法。
二、如何在教学中引入简易法做截面列剪力方程和弯矩方程绘制内力图虽然比较繁琐,却是引入简易法的基础。
在教学过程中要首先要详细讲解该方法。
在该方法的基础上引入简易法,很自然,也容易接受。
讲解根据内力方程绘制内力图时,首先要强调步骤,使学生有明确的绘制内力图思路。
该方法首先要对梁进行分段,这一步骤和简易法一致。
分段点是:杆的端点、集中力作用点、分布力的起点和终点。
在讲解的过程中,由于反复使用,学生的脑中会有比较深的印象;分段后,在每一段内任做一截面,将杆件一分为二,任取一局部,假设截面上的内力,根据局部的受力图列平衡方程求解内力方程;最后根据内力方程,绘制内力图。
为了总结不同载荷作用下内力图的形状及特点,在讲解根据内力方程绘制内力图时,要选择合适的例题。

第八章弯曲内力【学时】6(其中习题课2)【基本要求】1.理解平面弯曲的概念[2]。
2.掌握剪力方程和弯矩方程[2]。
3.掌握剪力图和弯矩图弯矩的绘制[2]。
4.了解叠加法作弯矩图[3]。
【重点】梁在任一指定截面处的剪力和弯矩值的计算;剪力方程和弯矩方程;剪力图和弯矩图。
【难点】弯矩、剪力和荷载集度间的微分关系。
§8-1 平面弯曲的概念和实例一、弯曲的概念1. 弯曲: 杆受垂直于轴线的外力或外力偶矩矢的作用时,轴线变成了曲线,这种变形称为弯曲。
2. 梁:以弯曲变形为主的构件通常称为梁。
3. 工程实例4. 平面弯曲:杆发生弯曲变形后,轴线仍然和外力在同一平面内。
对称弯曲(如下图)——平面弯曲的特例。
二、梁的计算简图梁的支承条件与载荷情况一般都比较复杂,为了便于分析计算,应进行必要的简化,抽象出计算简图。
1. 构件本身的简化:通常取梁的轴线来代替梁。
2. 载荷简化:作用于梁上的载荷(包括支座反力)可简化为三种类型:集中力、集中力偶和分布载荷。
3. 支座简化①固定铰支座2个约束,1个自由度。
如:桥梁下的固定支座,止推滚珠轴承等。
②可动铰支座 1个约束,2个自由度。
如:桥梁下的辊轴支座,滚珠轴承等。
③固定端 3个约束,0个自由度。
如:游泳池的跳水板支座,木桩下端的支座等。
4.静定梁的三种基本形式③外伸梁§8-2 弯曲时的内力——剪力和弯矩一、弯曲内力[举例]已知:如图,P ,a ,l 。
求:距A 端x 处截面上内力。
解:①求外力la l P Y Y lPaR m X X A B A A )(, 0 ,00 , 0-=∑∴==∑∴==∑∴=②求内力——截面法X A Y AM Axx Y M m l a l P Y Q Y A C A ⋅=∑∴=-==∑∴=, 0)(, 0∴ 弯曲构件内力⎪⎩⎪⎨⎧弯矩剪力1. 弯矩:M构件受弯时,横截面上其作用面垂直于截面的内力偶矩。
2. 剪力:Q构件受弯时,横截面上其作用线平行于截面的内力。




第八章弯曲应力与弯曲变形前面曾讨论了弯曲内力计算、内力图的绘制和平面几何性质,本章将解决弯曲的强度和刚度问题。
【能力目标、知识目标与学习要求】本章学习目标,知识目标和学习要求:本章学习内容要求学生熟练掌握弯曲强度计算的方法以及强度条件的应用,熟悉简单荷载作用下,用叠加法计算弯曲变形。
第一节弯曲应力本节将在第七章的基础上,进一步研究梁的横截面上内力的分布情况,即研究横截面上各点的应力。
通过研究,找出应力的分布规律,推导出应力的计算公式,从而解决梁的强度计算问题。
本节将分别讨论正应力σ和剪应力τ在横截面上的分布规律及其计算。
一、弯曲应力的种类由轴向拉伸与压缩和圆轴扭转可知,应力是与内力的形式相联系的,它们的关系是:应力为横截面上分布内力的集度。
梁弯曲时,横截面上一般是产生两种内力——剪力FQ和弯矩M(图8-1),这些内力皆是该截面内力系合成的结果。
由于剪力FQ是和横截面相切的内力,所以它是与横截面相切的剪应力的合力;而弯矩M则是作用面与横截面垂直的力偶矩,故它是由与横截面垂直的正应力合成的结果。
总之,由于梁的横截面上一般同时存在弯矩M和剪力FQ,所以,梁的横截面上σ,又有剪应力τ。
一般既有正应力二、弯曲正应力计算1、纯弯曲时梁横截面上的正应力:如图8-2所示的梁AB,CD段内只有弯矩而无剪力,这种情况称为纯弯曲。
而AC和DB段内各横截面上既有剪力还有弯矩.这种情况称为横力弯曲(剪切弯曲)。
在推导梁的正应力公式时,为了便于研究,我们从“纯弯曲”的情况进行推导。
F F(a)(b)(c)M 图Fal图 8-2(1)实验观察与分析:为了便于观察,采用矩形截面的橡皮梁进行试验。
实验前,在梁的侧面画上一些水平的纵向线pp 、ss 等和与纵向线相垂直的横向线mm 、nn 等(图8-3a),然后在对称位置上加集中荷载F(图8-3b)。
梁受力后产生对称变形,且可看到下列现象:1)变形前互相平行的纵向直线(pp 、ss 等),变形后均变为互相平行的圆弧线('p 'p 、''s s 等),且靠上部的缩短,靠下部的伸长。