Origin8.0画频率分布直方图与曲线拟合方法

Origin8.0画频率分布直方图与曲线拟合实例本文基于Origin8.0Origin8.0下载地址：/tp1939526328（此下载地址从3月12日起31天内有效）本文只用于来不及学习origin而又要交实验报告的同学们。

首先打开origin8.0 默认的界面如下，这里的格式应当是Book类型的。

1.首先，你可以先输入数据，如果你嫌在origin中输入太麻烦，而且和你的记录格式（比如是10*20的列表），你可以考虑在Excel中输入，再通过origin中：File>>Import>>Excel(XLS,XLSX)在Excel中输入：再将数据形式转化为：导入（import）origin：如下，直接按OK：接下来就是如下画面（那个小窗口可以关掉）：2.然后就是数据处理了左键单击A(X)，选中所有你输入的数据在A(X)栏单击右键，在菜单选择"Frequency Count..."即频数统计弹出如下窗口各项设置如下：然后按OK 就行了然后你会看到：按住"Ctrl" 键同时选中Bin Center(X) 和Freqs(Y)单击左下方的画出直方图3.这时候你可能还需要拟合正态分布曲线在Graph 的视图下，也就是有图片的那个视图下在上方，依次单击Analysis>>Fitting>>Nonliner Curve Fit （曲线拟合）(>>Open Dialog 如果你不是第一次使用曲线拟合，就要在单击这个了）弹出如下窗口：function 栏已经是Gauss（高斯）函数，只是这里的Guass函数与我们平时看到的有点不一样，但如果仅仅是拟合曲线，系数什么的不是我们所关心的，当然，为了看到熟悉的系数，我还是选择了另一个更为接近的高斯函数单击Fit 进行拟合弹出如下窗口，随意选择即可，默认为yes然后你就得到拟合曲线了4.你可以对图像进行进一步的修饰了：在左侧的工具栏你可以选择T 工具进行文字的添加，在图像上拖动，在弹出窗口中输入文字。

origin曲线分段拟合
Origin曲线分段拟合可以采用以下步骤：
1. 在origin中打开需要拟合的数据。

2. 在菜单栏中依次选择“Analysis”-“Fitting”-“Nonlinear Curve Fit”-“Multi 峰值拟合”。

3. 在弹出的对话框中，选择合适的函数类型，例如“Gaussian peaks”高斯峰，然后单击“Fit”按钮进行拟合。

4. 拟合完成后，可以在origin中查看拟合曲线和数据点，并根据需要调整参数和拟合曲线。

5. 如果需要对多个数据进行分段拟合，可以使用“Fitting”菜单下的“Piecewise Linear Fit”逐段线性拟合。

在弹出的对话框中，根据需要设置分段点，并选择合适的拟合类型，例如“Linear”线性拟合或“Quadratic”二次拟合等。

6. 单击“Fit”按钮进行拟合，并在origin中查看拟合曲线和数据点。

7. 如果需要调整分段点的位置或拟合曲线的参数，可以在origin中进行手动调整或使用“Peak Fitting”菜单下的相关选项进行微调。

通过以上步骤，可以在origin中进行曲线分段拟合，并获得更好的拟合效果。

origin8.0拟合曲线的方程
拟合曲线的方程可以是多种形式，取决于所拟合的数据类型和所使用的拟合方法。

以下是几种常见的拟合曲线方程：
1. 线性拟合方程：y = mx + c
适用于线性关系，其中 m 是斜率，c 是截距。

2. 多项式拟合方程：y = a0 + a1*x + a2*x^2 + ... + an*x^n
适用于非线性关系，其中 a0, a1, ..., an 是多项式的系数，n
为拟合阶数。

3. 指数拟合方程：y = a * exp(b*x)
适用于呈指数增长或衰减的关系，其中 a 和 b 是拟合参数。

4. 对数拟合方程：y = a * ln(b*x)
适用于呈对数关系，其中 a 和 b 是拟合参数。

5. 幂函数拟合方程：y = a * x^b
适用于呈幂函数关系，其中 a 和 b 是拟合参数。

这些方程只是常见的拟合曲线方程示例，具体情况还需根据数据特征和所使用的拟合方法来确定最适合的方程形式。

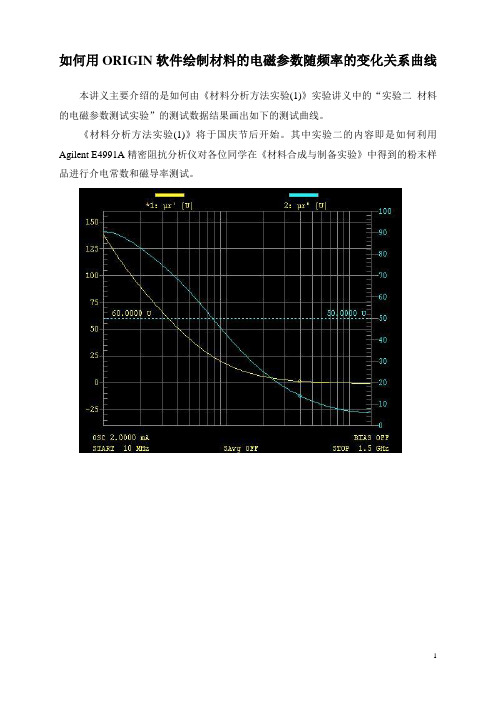
如何用ORIGIN软件绘制材料的电磁参数随频率的变化关系曲线本讲义主要介绍的是如何由《材料分析方法实验(1)》实验讲义中的“实验二材料的电磁参数测试实验”的测试数据结果画出如下的测试曲线。

《材料分析方法实验(1)》将于国庆节后开始。

其中实验二的内容即是如何利用Agilent E4991A精密阻抗分析仪对各位同学在《材料合成与制备实验》中得到的粉末样品进行介电常数和磁导率测试。

1．利用Agilent E4991A保存的文件为后缀为TXT的（**.TXT）数据文件，如图1所示。

图1将该文件打开后即为测试的数据结果。

第一列为频率值，第二列为测试的磁导率实部值。

2．将该数据导入ORIGIN软件：点击鼠标右键，在打开方式中选择“Origin”。

将该文件用ORIGIN 程序打开。

图23．在ORIGIN的打开界面中，会出现如图3所示的提示，一直点击“Next 〉〉”，直到最后一步“Finish”。

则测试数据就被导入到ORIGIN中来了，如图4所示。

图3图44．在“Column”下拉菜单中选择“Add New Columns”添加新的数据栏，以方便整理数据。

如图5所示。

我们在此添加3栏。

图55．本TXT文件中包含了材料磁导率的实部和虚部两个测试结果。

要把虚部的测试数据放到不同的数据栏内。

选择207行以后的数据，将其剪切到新添加的两栏内，如图6所示。

同时删除204和205行的无用数据。

图66．将C、D栏中第一行中的“Frequency”和“Data”删除，以保证C列和A列的频率是一一对应的。

如图7所示。

图77．图7的数据中，A列和C列表示的是测试频率，也就是最终绘图中的X坐标轴，将其设为X轴，选中C列数据，点击鼠标右键，在“Set As”中选择“X”，如图8所示。

图88．因为测试频率的单位为Hz，测试数值太大（1×107），我们在此将频率单位改为MHz，也就是将A列和C列的数值都除以1000000（106，即1E6）。

Origin 是一款常用于数据分析和绘图的软件。

其中一个功能就是曲线拟合，即找到曲线与一组数据点的最佳拟合。

该软件允许您使用多种模型来拟合数据，包括多项式、指数、对数和幂函数。

在Origin中，您可以通过选择要拟合的数据，然后从分析菜单中选择要使用的函数类型来执行曲线拟合。

软件将生成数据的图表，并在其中显示拟合曲线、拟合方程和系数。

您还可以使用该软件对拟合进行各种统计测试，如拟合优度测试或确定参数的置信区间。

拟合完成后，您还可以使用软件绘制残差（观测数据与拟合值之间的差异）和绘制拟合参数的置信区间。

总之，Origin 是一个功能强大的数据分析工具，可以帮助您轻松地将曲线拟合到数据中并从中提取有用信息。

origin拟合标准曲线在科学研究中，数据拟合是非常重要的一环。

而拟合标准曲线的过程中，比较常见的一种方法就是利用“origin”这一工具。

下面我们就来介绍一下如何利用“origin”进行标准曲线的拟合。

步骤一：准备数据首先，我们需要先准备好需要拟合的数据集。

这些数据应该以表格的形式存储，并且要求数据清晰、完整。

在具体的实验操作中，我们可以将数据直接以excel表的形式导入到“origin”软件中。

步骤二：导入数据打开“origin”软件后，我们首先需要将之前准备好的数据导入进去。

具体地，我们可以通过点击“File-->Import-->ASCII”，然后找到之前保存的excel表格并打开。

此时，“origin”就会自动将数据导入到一个新窗口，并且会显示出数据表格。

步骤三：绘制数据在“origin”中，我们可以通过绘图的方式来展示数据。

为了能够更好地分析数据并拟合标准曲线，我们需要将数据绘制成散点图。

具体地，我们可以在数据窗口中选择需要绘制的数据列，然后选择“Plot-->Scatter”即可绘制散点图。

步骤四：选择拟合函数接下来，我们需要选择一种合适的函数来拟合我们的数据。

在“origin”中，有许多拟合函数可供选择，包括线性、多项式、指数、对数等等。

在选择时，我们需要根据具体的数据特征和研究目的来进行判断。

例如，在某些情况下，我们可以选择“Logistic”函数来拟合生长曲线。

步骤五：拟合曲线选择好合适的函数后，我们就可以利用“origin”软件来进行曲线拟合了。

具体地，我们可以在散点图窗口中，选择“Analysis-->Fitting-->Nonlinear Curve Fit”来进入拟合曲线的设置界面。

在这里，我们需要选择之前选定好的函数，并设置一些拟合参数，例如起始值、上限值等等。

设置好后，我们点击“Fit”按钮，软件就会自动进行曲线拟合，并将拟合结果以曲线的形式展示出来。

origin数据拟合成曲线摘要：一、引言二、Origin数据拟合原理1.线性拟合2.非线性拟合三、拟合步骤1.数据准备2.添加拟合项3.设置拟合参数4.分析拟合结果四、优化拟合效果1.选择合适的拟合函数2.调整拟合参数3.增加或删除拟合项五、实例演示1.线性拟合实例2.非线性拟合实例六、总结与展望正文：一、引言作为一款强大的数据处理软件，Origin在科学计算、数据分析领域得到了广泛的应用。

其中，数据拟合功能可以帮助我们将实验或观测得到的数据转化为具有特定数学关系的曲线。

本文将详细介绍如何使用Origin进行数据拟合，以及如何优化拟合效果。

二、Origin数据拟合原理Origin数据拟合主要包括线性拟合和非线性拟合。

1.线性拟合：线性拟合是将数据点拟合成一条直线，其主要应用于数据呈线性关系的情况。

Origin软件会自动计算线性方程的斜率和截距，从而得到拟合方程。

2.非线性拟合：非线性拟合是将数据点拟合成一条非线性曲线，如二次曲线、指数曲线等。

Origin软件支持多种非线性拟合函数，用户可以根据实际情况选择合适的函数进行拟合。

三、拟合步骤1.数据准备：首先，在Origin软件中导入需要拟合的数据。

可以通过直接输入数据、导入文本文件或Excel文件等方式完成。

2.添加拟合项：在Origin中，选择需要拟合的数据集，右键点击，选择“拟合”菜单，添加拟合项。

用户可以根据需要选择线性拟合或非线性拟合。

3.设置拟合参数：在拟合项对话框中，可以设置拟合参数，如拟合函数、初始参数等。

根据实际需求，用户可以调整拟合参数以优化拟合效果。

4.分析拟合结果：完成拟合后，Origin软件会自动生成拟合报告，包括拟合方程、拟合参数、拟合精度等信息。

用户可以根据这些信息判断拟合效果是否满足要求。

四、优化拟合效果1.选择合适的拟合函数：根据数据特点，选择合适的拟合函数。

例如，当数据呈二次关系时，应选择二次拟合函数；当数据呈指数关系时，应选择指数拟合函数。

origin拟合的曲线
Origin软件是一款常用的科学数据处理和绘图软件，其拟合曲线主要基于以下两种方式：
1. 线性拟合（Linear Fit）：这种拟合方法通过输入的数据点进行线性拟合，可以拟合直线、二次项和三次项等线性关系。

具体步骤包括在软件中导入数据、选择拟合类型、设置拟合参数、进行拟合等。

2. 非线性拟合（Nonlinear Fit）：这种拟合方法适用于更复杂的非线性关系，如指数、对数、幂等。

在Origin中，可以通过选择合适的函数类型和参数进行非线性拟合。

以上是Origin软件中常见的两种拟合曲线方式，具体的操作步骤可能会因为软件的版本和功能而有所不同。

如有需要，可以参考软件的使用手册或在线教程。

origin曲线拟合方程「origin曲线拟合方程」是一种常见的数学工具，用于将散乱的数据点拟合成符合某种函数形式的连续曲线。

在科研、工程设计以及数据分析等领域中，这种工具可以帮助人们快速、准确地理解数据、发现规律、做出预测，从而更好地服务于人们的需求。

那么，「origin曲线拟合方程」究竟是什么？它具体包括哪些步骤？首先，我们需要明确一下拟合曲线的形式。

在「origin曲线拟合方程」中，最常见的曲线形式是多项式函数，即：y = a0 + a1*x + a2*x^2 + ... + an*x^n其中，y是因变量，x是自变量，a0~an是系数，n表示多项式的最高次数。

不同的数据集可能需要不同次数的多项式才能较好地拟合，因此，选择合适的多项式次数可以提高拟合效果。

其次，我们需要导入「origin曲线拟合方程」工具。

在使用origin软件创建新图像之后，我们可以进入“分析”菜单，找到“曲线拟合”选项。

在弹出的对话框中，我们可以选择想要拟合的数据集以及拟合的类型。

在此，我们选择“多项式”类型，并手动输入需要拟合的多项式次数。

然后，我们可以按照提示完成剩下的设置，例如设置系数精度、画图方式等。

接着，我们可以预览拟合的结果。

在完成前面的设置后，我们可以预览拟合曲线和数据点的对比。

如果发现拟合效果不佳，我们可以返回对话框，重新设置多项式次数或者其他参数，直到满意为止。

最后，我们可以导出拟合方程。

在完成对曲线拟合的调整后，我们可以导出拟合方程，即多项式的系数值。

这些系数可以用来进行数据预测、分析和优化。

通过这些步骤，我们可以使用「origin曲线拟合方程」工具有效地理解、处理和利用散乱的数据。

当然，在使用过程中，我们也需要注意一些问题，例如需选择合适的拟合函数、注意曲线拟合的误差限制等。

在熟练掌握这些技巧后，「origin曲线拟合方程」可以成为我们处理科研和数据分析中常见问题的有力工具。

Origin8.0画频率分布直方图与曲线拟合实例本文基于Origin8.0本文只用于来不及学习origin而又要交实验报告的同学们。

首先打开origin8.0 默认的界面如下，这里的格式应当是Book类型的。

1.首先，你可以先输入数据，如果你嫌在origin中输入太麻烦，而且和你的记录格式（比如是10*20的列表），你可以考虑在Excel中输入，再通过origin中：File>>Import>>Excel(XLS,XLSX)在Excel中输入：再将数据形式转化为：导入（import）origin：如下，直接按OK：接下来就是如下画面（那个小窗口可以关掉）：2.然后就是数据处理了左键单击A(X)，选中所有你输入的数据在A(X)栏单击右键，在菜单选择"Frequency Count..."即频数统计弹出如下窗口各项设置如下：然后按OK 就行了然后你会看到：按住"Ctrl" 键同时选中Bin Center(X) 和Freqs(Y)单击左下方的画出直方图3.这时候你可能还需要拟合正态分布曲线在Graph 的视图下，也就是有图片的那个视图下在上方，依次单击Analysis>>Fitting>>Nonliner Curve Fit （曲线拟合）(>>Open Dialog 如果你不是第一次使用曲线拟合，就要在单击这个了）弹出如下窗口：function 栏已经是Gauss（高斯）函数，只是这里的Guass函数与我们平时看到的有点不一样，但如果仅仅是拟合曲线，系数什么的不是我们所关心的，当然，为了看到熟悉的系数，我还是选择了另一个更为接近的高斯函数单击Fit 进行拟合弹出如下窗口，随意选择即可，默认为yes然后你就得到拟合曲线了4.你可以对图像进行进一步的修饰了：在左侧的工具栏你可以选择T 工具进行文字的添加，在图像上拖动，在弹出窗口中输入文字。

origin多项式拟合曲线
Origin软件是一款常用的绘图软件，在曲线拟合方面提供了多
项式拟合功能。

多项式拟合是一种基于最小二乘原理的曲线拟合方法，可以用来拟合各种非线性曲线。

下面介绍在Origin
中进行多项式拟合曲线的具体步骤：
1. 导入数据：在Origin中新建一个工作表，将需要拟合的数
据输入到该工作表中。

2. 选择数据：选中需要拟合的数据，右键单击弹出菜单，选择"Analysis"-"Fitting"-"Polynomial Fit"。

3. 多项式设置：在多项式拟合对话框中，选择要拟合的最高次数，并选择是否对截距进行约束。

点击"OK"开始拟合。

4. 拟合结果：拟合完成后，Origin将会生成一个多项式曲线拟
合图，并将拟合结果显示在图形中。

同时，在工作表中会添加一个新列，该列包含了拟合后的拟合值。

5. 优化拟合曲线：在拟合曲线图中，可以进一步调整拟合参数，如改变拟合次数、添加噪声、设置初始值等，以优化拟合结果。

6. 输出结果：完成拟合后，可以将拟合结果导出为各种格式，如图片、表格、文本等。

以上就是在Origin中进行多项式拟合曲线的基本步骤。

更加
详细的操作方法可以参考Origin软件自带的帮助文档。

origin曲线拟合Origin曲线拟合可以被称为数据分析的一种基础的技术。

它可以帮助研究者根据给定的实验数据来构建一个更为准确的模型。

从理论上讲，Origin曲线拟合有许多优点，可以有效地帮助研究者从海量数据中挖掘出实际有用的信息，并且可以弥补人类观察力的局限性。

Origin曲线拟合的基本原理是利用特定的曲线函数，如多项式、指数、对数等，拟合出与一组已知的实验黑点值最接近的一条曲线，从而实现对数据的准确描述。

因此，Origin曲线拟合的步骤为：第一步，根据实验数据，确定可能的拟合函数；第二步，调整拟合函数的参数，并用特定的优化算法求出使绝对值最小的参数；第三步，根据最优参数计算出拟合曲线；输出拟合曲线图；第四步，根据拟合曲线的表现，获取有用的结论。

Origin曲线拟合的应用可以说是极其广泛的，几乎涉及到各个领域。

通常，在物理、化学、生物等实验中，数据是比较多而杂乱的，往往难以找出其真正含义。

而Origin曲线拟合可以帮助研究者从数据中提取出实际有用的信息，甚至可以用拟合函数来描述一个实验过程，从而为实验结果提供有效的理论依据。

此外，Origin曲线拟合也可以用来对不可知曲线进行合理预测，因为它可以根据少量的实验数据，来构建一个正确的拟合曲线，从而获取大量的数据，用于预测仪器的行为。

例如，在工程设计中，Origin 曲线拟合可以根据实验数据来计算出一个正确的拟合曲线，模拟出整个工程设计过程，从而有助于建立正确的结论，提高工程设计的效率。

最后，需要指出的是，Origin曲线拟合有一定的局限性，它假设所有的数据满足一定拟合函数的要求，不能有效地处理原始数据的噪音；同时，它的精度也受到实验数据的质量的限制，只有当实验数据足够准确时，才能得出较为准确的拟合曲线图。

所以，在获取实验数据时，研究者和工程师都应该尽量采用较为可靠的实验方法，以保证Origin曲线拟合的准确性和精度。

综上所述，Origin曲线拟合可以被认为是数据分析的基础技术，其应用非常广泛，在实验数据的获取、分析、模拟等方面都有重要作用。

origin 峰值拟合曲线
Origin软件是一款常用的科学数据处理和图形绘制软件，可以用于峰值拟合和曲线绘制。

以下是使用Origin进行峰值拟合和曲线绘制的步骤：
1.数据导入：将需要拟合的数据导入Origin软件中，可以通过复制粘贴、导入数据文件等方式完成。

2.绘制曲线：在Origin中选择“绘图”菜单，选择适合的数据图表类型，例如散点图、线图等，然后将数据添加到图表中，即可绘制出相应的曲线。

3.峰值拟合：在Origin中选择“分析”菜单，选择“峰值分析”选项，并选择适合的峰值拟合函数类型，例如Lorentz函数、Gaussian函数等。

然后根据需要进行参数设置和调整，并点击“拟合”按钮，即可完成峰值拟合。

4.结果分析：Origin会给出拟合结果的详细信息，包括拟合函数参数、拟合优度等。

用户可以根据需要进行进一步的数据分析和处理。

需要注意的是，在进行峰值拟合时，应选择适合的拟合函数类型，并根据实际情况进行参数设置和调整。

同时，对于复杂的数据，可能需要采用多种方法进行拟合和分析，以获得更准确的结果。