泛珠三角物理竞赛1~11届大全

40届中学生物理竞赛预赛获奖名单第40届中学生物理竞赛预赛获奖名单一、团体奖本次竞赛的团体奖分为一等奖、二等奖和三等奖。

一等奖1. 天津市实验中学2. 上海交通大学附属中学3. 北京市第四中学4. 成都市第七中学5. 广州市实验中学6. 南京市金陵中学7. 武汉市第一中学8. 西安市第九中学9. 成都市七中10. 上海市徐汇中学二等奖11. 沈阳市第一中学12. 长沙市第四中学13. 南宁市第四中学14. 青岛市第二中学15. 大连市第八中学16. 重庆南开中学三等奖17. 哈尔滨市实验中学18. 石家庄市第一中学19. 深圳市高级中学20. 苏州市第一中学21. 杭州市第七中学22. 长春市第一中学二、个人奖个人奖分为最佳个人奖、一等奖、二等奖和三等奖。

最佳个人奖姓名：张小龙学校：上海交通大学附属中学一等奖1. 李明，天津市实验中学2. 王芳，北京市第四中学3. 张翔，成都市第七中学4. 王云，广州市实验中学5. 杨波，南京市金陵中学6. 刘明，武汉市第一中学7. 张全，西安市第九中学8. 陈阳，成都市七中9. 赵彬，上海市徐汇中学10. 杨帆，沈阳市第一中学二等奖11. 顾琪，长沙市第四中学12. 陈涛，南宁市第四中学13. 刘璇，青岛市第二中学14. 胡阳，大连市第八中学15. 李志远，重庆南开中学三等奖16. 刘亚，哈尔滨市实验中学17. 王东海，石家庄市第一中学18. 赵磊，深圳市高级中学19. 李洋，苏州市第一中学20. 许晨，杭州市第七中学21. 张明明，长春市第一中学三、颁奖典礼本次竞赛的颁奖典礼将于7月20日在北京市举行。

届时，获奖者和各中学的代表将齐聚一堂，共同庆祝他们的成果和努力。

当日的颁奖典礼将精彩纷呈，除了颁发团体奖和个人奖之外，还有精彩的表演节目和颁发荣誉证书。

此外，颁奖典礼还将举办座谈会，邀请教育专家和竞赛优胜者代表进行互动交流。

届时，获奖者们将有机会与教育界的权威人士进行面对面的交流，分享自己的学习心得和经验。

全国中学生物理竞赛分类汇编光学11第21届预赛一、（15分）填空1．d．一个可见光光子的能量的数量级为_________J。

2．已知某个平面镜反射的光能量为入射光能量的80％。

试判断下列说法是否正确，并简述理由。

a．反射光子数为入射光子数的80％；b．每个反射光子的能量是入射光子能量的80％。

心在顶点O下方玻璃中的C点，球面的半径R＝1.50cm，O到杯口平面的距离为8.0cm。

在杯脚底中心处P点紧贴一张画片，P点距O点6.3cm。

这种酒杯未斟酒时，若在杯口处向杯底方向观看，看不出画片上的景物，但如果斟了酒，再在杯口处向杯底方向观看，将看到画片上的景物。

已知玻璃的折射率n1＝1.56，酒的折射率n2＝1.34。

试通过分析计算与论证解释这一现象。

四、(20分)目前，大功率半导体激光器的主要结构形式是由许多发光区等距离地排列在一条直线上的长条状，通常称为激光二极管条．但这样的半导体激光器发出的是很多束发散光束，光能分布很不集中，不利于传输和应用．为了解决这个问题，需要根据具体应用的要求，对光束进行必需的变换（或称整形）．如果能把一个半导体激光二极管条发出的光变换成一束很细的平行光束，对半导体激光的传输和应用将是非常有意义的．为此，有人提出了先把多束发散光会聚到一点，再变换为平行光的方案，其基本原理可通过如下所述的简化了的情况来说明．如图，S 1、S 2、S 3 是等距离（h ）地排列在一直线上的三个点光源，各自向垂直于它们的连线的同一方向发出半顶角为 =arctan ()41的圆锥形光束．请使用三个完全相同的、焦距为f = 1.50h 、半径为r =0.75 h 的圆形薄凸透镜，经加工、组装成一个三者在同一平面内的组合透镜，使三束光都能全部投射到这个组合透镜上，且经透镜折射后的光线能全部会聚于z 轴（以S 2为起点，垂直于三个点光源连线，与光束中心线方向相同的射线）上距离S 2为 L = 12.0 h 处的P 点．（加工时可对透镜进行外形的改变，但不能改变透镜焦距．）1．求出组合透镜中每个透镜光心的位置．2．说明对三个透镜应如何加工和组装，并求出有关数据．图所示．已知L1的焦距f1=f , L2的焦距f2=—f，两透镜间距离也是f．小物体位于物面P上，物距u1＝3f．（1）小物体经这两个透镜所成的像在L2的__________边，到L2的距离为_________，是__________倍（虚或实）、____________像（正或倒），放大率为_________________。

Pan Pearl River Delta Physics Olympiad 20062006年泛珠江三角物理竞赛Part-1 卷-1(9:00 am -12:00 pm, 02-09-2006)Q1 (8 points)题1 (8 分)Electron 电子Meson介子芥子由两个夸克构成，而夸克之间的相互作用相当复杂。

研究介子可通过用高能电子与之作非弹性碰撞来进行。

由于碰撞过程难于分析，为掌握其主要内涵，人们发展了一种简化了的‘分粒子’模型。

其主要内容为：电子只和介子的某部分（比如其中一个夸克）作弹性碰撞。

碰撞后的夸克再经过介子内的相互作用把能量和动量传给整个介子。

模型的主要精神可用下面的简化模型来阐述：一电子质量为m1,动能为E，与介子的一个夸克（质量m2）作弹性碰撞。

介子里另一个夸克的质量为m3。

夸克间以一无质量弹簧相连。

碰撞前夸克处于静止状态，弹簧处于自然长度。

所有运动都是一维的。

忽略一切相对论效应。

求碰撞后以弹簧振动形式代表的介子内能，和介子作为一整体所具有的动能。

Q2 (8 points)题2 (8 分)一均匀铁滑轮质量为M1，半径为R，固定在地面上方。

滑轮可以轮心自由转动。

另有总重量为M2的许多小磁铁块可吸附在滑轮上。

一长细绳绕着滑轮边缘，终端挂一质量为M3的小重块，离地高度为H。

细绳与滑轮间无滑动。

（a）问小磁铁块应怎样圆对称地分布在滑轮上，才能使小重块被放开后到达地面时的速度为最小？（b）求该速度。

Q3 （10 points）题 3 （10 分）一圆柱容器半径为R，装有高度达H的水（密度为P）。

（a）求水对容器面上一宽度为d（<< R < H）的竖直面的压力。

（3分）（b）将容器放在以角速度3（< v gH/R）转动的转台上，转动轴与容器中心轴重合。

水的转动和转台一致。

求水面形状和水对竖直面因转动而带来的附加压力。

（g为重力加速度。

）（7分）Q4 (12 points)题 4 (12 分)Pan Pearl River Delta Physics Olympiad泛珠三角物理竞赛2006一固定体积为V 的汽室中间由一可左右无磨擦滑动的轻活塞分开。

泛珠⼒学基础试试题及答案-PanPhO2011_Mechanics⾹港物理奧林匹克委員會主辦中國教育學會物理教學專業委員會協辦第七屆泛珠三⾓物理奧林匹克暨中華名校邀請賽⼒學基礎試賽題(2011年2⽉10⽇9:00-12:00)**有需要时,如⽆说明,取g =10m/s 2; G =6.67×10?11Nm 2/kg 2. ***** 选择题1⾄16(48分,答案唯⼀)和简答题17⾄20(52分),做在答题纸上.***1. ⼀位观察者站在静⽌的列车第⼀节车厢的前端。

当列车以等加速度开动时，第⼀节车厢经过其旁需5s ，则第⼗节车厢经过其旁的时间⼤约是A. 1.18sB. 1.07sC. 0.98sD. 0.91sE. 0.86sF. 0.81s2. 如图所⽰，两个⽤轻线相连的位于光滑⽔平⾯上的物块，质量分别为m l 和m 2，拉⼒F 1和F 2⽅向相反，与刚度系数为k 的轻线沿同⼀⽔平直线运动，且F 1>F 2。

在两个物块运动过程中轻线的伸长x 为 A.212211m m k m F m F ?+ B.)(212211m m k m F m F ++ C.)(212211m m k m F m F +? D.)(211221m m k m F m F +? E.)(211221m m k m F m F ++ F.211221m m k m F m F ?+ 3. 如图所⽰，⼀质量为M 的三⾓形⽊块放在⽔平桌⾯上，它的顶⾓为900，两底⾓为α和β，两个质量均为m 的⼩⽊块位于両侧斜⾯上。

⼰知所有接触⾯都是光滑的。

现发现两⼩⽊块沿斜⾯下滑，⽽模形⽊块静⽌不动，这时三⾓形⽊块对⽔平桌⾯的压⼒等于A. MgB. 2mgC. Mg +2mgD. Mg +mgE. Mg +mg (βαsin sin +)F. Mg +mg (βαcos cos +) (题4-5) ⼀个倾⾓为α的固定斜⾯上，在斜⾯底部有⼀⼩物块。

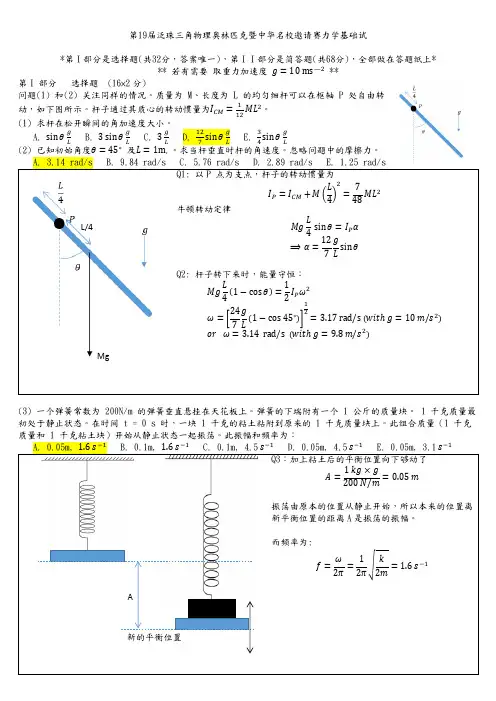
第19届泛珠三角物理奥林匹克暨中华名校邀请赛力学基础试*第Ｉ部分是选择题(共32分，答案唯一)，第ＩＩ部分是简答题(共68分)，全部做在答题纸上*** 若有需要 取重力加速度 g =10 ms —2 **第I 部分 选择题 (16×2分)问题(1) 和(2) 关注同样的情况。

质量为 M 、长度为 L 的均匀细杆可以在枢轴 P 处自由转动，如下图所示。

杆子通过其质心的转动惯量为I CM =112ML 2。

(1) 求杆在松开瞬间的角加速度大小。

A. sin θgL B. 3sin θgL C. 3gL D. 127sin θgL E. 34sin θgL∘A. 3.14 rad/s B. 9.84 rad/s C. 5.76 rad/s D. 2.89 rad/s E. 1.25 rad/sQ1: 以P 点为支点，杆子的转动惯量为I P =I CM +M (L 4)2=748ML 2牛顿转动定律Mg L4sin θ=I P α ⟹α=127gLsin θQ2: 杆子转下来时，能量守恒：Mg L 4(1−cos θ)=12I P ω2ω=[247gL(1−cos 45∘)]12=3.17 rad/s (witℎ g =10 m/s 2) or ω=3.14 rad/s (witℎ g =9.8 m/s 2)(3) 一个弹簧常数为 200N/m 的弹簧垂直悬挂在天花板上。

弹簧的下端附有一个 1 公斤的质量块。

1 千克质量最初处于静止状态。

在时间 t = 0 s 时，一块 1 千克的粘土粘附到原来的 1 千克质量块上。

此组合质量（1 千克A. 0.05m, 1.6 s B. 0.1m, 1.6 s C. 0.1m, 4.5 s D. 0.05m, 4.5 s E. 0.05m, 3.1 sQ3：加上粘土后的平衡位置向下够动了A =1 kg ×g 200 N/m=0.05 m振荡由原本的位置从静止开始，所以本来的位置离新平衡位置的距离A 是振荡的振幅。

2020年第16届泛珠三角物理奥林匹克竞赛力学基础试题一、单选题1．图标某人做不同类型运动的速度向量v 和加速度向量a 、哪种情况下此人放慢速度并向右转？（ ）A ．B ．C ．D ．E ．F ．一质量为m 的无动力飞船以初速度0v 从远处飞向一质量为()M m >>的行星。

如果行星周围不存在引力场，飞船会在离行星最近距离0d 处以直线航线飞过（如图中虚线所示）。

2．设20GMv γ=，飞船实际离行星最近的距离为（飞船的实际航线如实线所示）（ ） AγBCγDγEFγ3．设20GMv γ=，当飞船飞过并远离行星后的最终速率是（ ） A ．02v B ．053v C ．032v D ．43v E ．0v F ．034v一质量为m 的滑块，静止在轨道上距离地面高度为h 处，其下端是半径为R 的圆形轨道，问题中所有摩擦力忽略不计。

4．若滑块能够到达圆形轨道的最高点P ，则初始高度的最小值min h =（ ） A ．1.577R B ．1.866R C ．2.25R D ．2.5RE ．3.0RF ．3.5R5．当min h h <时，滑块会在轨道上某点Q 离开轨道做斜抛运动，并且击中圆心O 点。

设滑块在Q点做斜抛运动的速度θ，则k 和θ为（ ）A ．0.84和45.0︒B ．0.80和50.8︒C ．0.76和54.7︒D ．0.73和57.7︒E ．0.71和60.0︒F ．0.70和61.5︒6．若滑块最后击中O 点，其在轨道上初高度h =（ ） A ．1.577R B ．1.866R C ．2.25R D ．2.5R E ．3.0RF ．3.5R一质量为M 的光滑大圆环用细绳挂在天花板上。

两个质量同为m 的小圆圈从环顶由静止开始同时向两边下滑，已知质量比M K m=。

7．当细绳张力0T =时圆圈位置θ的余弦函数cos x θ=满足方程（ ） A ．2460x x K -+= B ．2460x x K +-= C ．2320x x K -+= D ．2320x x K +-= E ．2640x x K -+= F ．2640x x K +-=8．参量K 的取值范围为（ ） A ．031K <≤ B ．021K <≤ C ．032K ≤≤D ．01K <≤E ．023K <≤F ．02K <≤9．当小圆圈的质量m 是大圆环质量M 的2倍且细绳张力0T =时，圆圈位置θ=（ ） A ．48︒ B ．51.5︒ C ．55︒ D ．60︒ E ．70.5︒ F ．84.4︒10．刚度50N /m k =和质量2kg M =的弹簧振子在光滑水平面上往复运动。

第一届泛珠三角物理奥林匹克竞赛（2005年1月29日上午）题1（5分） 光滑平面上有两条长度均为2 l 、而质量为m 的均匀蠕虫A 和B 。

它们的起始位置如图所示，蠕虫A 的质心位于x -y 坐标（0, 0）。

蠕虫B 开始慢慢从A 身上爬过，爬时两虫的身体轴线始终保持夹角。

试用参量l , θ 表示：当蠕虫B 爬过A 后，两蠕虫各个质心位置的坐标。

题2（13分）一体积为 0.001m 3 的空气泡和一质量和体积与空气泡相同的钢瓶从水下2.0 km 深处放出。

不考虑磨擦。

气泡温度不变。

空气在水面的密度为1.21 kg/m 3，大气压为1.0 x 105N/m 2。

(提示: ⎪⎪⎭⎫ ⎝⎛++=+⎰a b x dx ba βαβαββαln 1 )(a) 求气泡到水面时体积。

（3分）(b)求在深度 h (h < 2.0 km)时气泡和钢瓶净得的能量的表达式。

（7分） (c) 用该表达式求气泡和钢瓶到达水面时的速度。

（3分）题3（12分）一质量为0.5M 的人站在一以角速度ω旋转的厚度质量均匀，质量为0.5M ，半径为R 的圆台上。

圆台与中心转轴间无磨擦。

该人离圆台中心距离为r （< R ） ，并带有10颗质量为0.01M 的石子。

(a) 求整个系统的总角动量。

（4分）为了减速该人准备向外扔石子。

石子扔出时相对于他的速度为v ，方向与径向成夹角ϑ.(b) 求当他扔了一石子后圆台的角速度， 并找出使角速度减少最多的夹角m ax ϑ。

（4分） (c) 求当他以m ax ϑ扔光石子后圆台的角速度。

(答案可用多项式表达) （4分）题4（8分）一均匀长竿长度为L ，质量为M ，在一半径为R (>0.5L )的光滑半球面内处于静止状态。

(a) 求竿在其平衡位置附近作小幅振荡的频率。

（4分） (b) 已知小幅振荡时长竿偏离水平线最大偏角为m ax θ。

长竿在最大偏角和水平时球面对竿端的力的强度的差可写成2max θαMg N =∆。

第十三届泛珠三角物理基础试全文共四篇示例，供读者参考第一篇示例：第十三届泛珠三角物理基础试2022年是第十三届泛珠三角物理基础试的举办年份，这一学术盛事将汇聚来自泛珠三角地区的顶尖物理科学家和优秀学生，共同探讨物理学的最新研究成果和发展趋势。

作为本次比赛的主办方之一，我们将为您介绍这一项重要的科学赛事。

泛珠三角地区是中国广东省、香港特别行政区、澳门特别行政区以及台湾省和海外华人华侨居住地区的总称，这一地区拥有丰富的物理学研究资源和人才储备，是中国乃至全球物理学研究的重要中心之一。

每年举办的泛珠三角物理基础试吸引了来自各个高校和研究机构的优秀学生和研究人员参与，展现了泛珠三角地区物理学研究的最新成果和前沿技术。

本次第十三届泛珠三角物理基础试将包括理论物理、实验物理和计算物理三个竞赛项目，涵盖了物理学的各个领域和方向。

参赛选手将通过论文撰写、实验操作和计算模拟等方式展示自己的物理学知识和能力，与其他优秀学生一较高下。

本次比赛还将邀请相关领域的著名专家和学者组成评审团，对参赛作品进行评定和点评，为优胜者颁发奖项和荣誉证书。

在本次比赛中，我们将设立一等奖、二等奖、三等奖和优秀奖等多个奖项，以鼓励各位参赛选手发挥自己的聪明才智和创造力。

优秀的参赛作品不仅可以展示参赛选手的物理学水平，还可以为泛珠三角地区的物理学研究和发展注入新的活力和动力。

除了竞赛项目外，本次比赛还将举办一系列与物理学相关的学术交流活动，包括专题讲座、研讨会和学术展示等，为参与者提供学习和交流的机会。

借此机会，参赛选手将有机会与各地物理学专家和学者交流意见、学习经验，拓展自己的学术视野，提升自己的科学素养。

值得一提的是，本次比赛还将举办“泛珠三角物理之星”的评选活动，邀请各位物理科研工作者和相关领域的专家评选出在物理学领域中具有突出贡献和影响力的学生和研究人员，并为其颁发荣誉证书和奖金。

这一活动旨在表彰和鼓励在泛珠三角地区物理学研究领域中取得显著成就的个人和团体，为推动物理学的发展和繁荣做出贡献。

中国参加的历届国际物理奥林匹克竞赛成绩(2012完整版)注一；理论或实验成绩为满分则一并注明，信息未明或不清楚则未注明注二；2003年第34届国际物理奥林匹克竞赛在中国台湾举行，我国组队但没有参加，此名单一并补充完整。

)第17届(1986年，英国)林晨（男）北京师大二附中银牌卫星（男）四川绵阳核工业部九院一所子弟学校铜牌张明（男）安徽省全椒县中学荣誉纪念奖第18届(1987年，原德意志民主共和国)陈恂（男）湖北武汉一中银牌黎锦晖（男）山东实验中学银牌吴爱华（男）湖北荆州中学铜牌张燕平（男）北京四中铜牌唐鹏飞（男）四川简阳中学铜牌第19届(1988年，奥地利)陈岩松（男）福建师范大学附中金牌徐剑波（男）浙江鄞县中学银牌陈丰（男）江苏南箐中学银牌丁爱东（男）北京清华大学附中铜牌陈建（男）北京人大附中荣誉纪念奖第20届(1989年，波兰)葛宁（男）陕西电讯工程学院附中银牌燕京（男）北京四中银牌毛甬（男）浙江杭州四中银牌邱东昱（男）湖南长沙一中银牌林晓帆（男）陕西西安交大附中铜牌第21届（1990年，荷兰）吴明扬（男）陕西西安交大附中金牌周纲（男）浙江慈溪县中学金牌林巍（男）甘肃西北师大附中银牌段志勇（男）湖北武汉六中铜牌陈伯友（男）湖南长沙一中铜牌第22届(1991年，古巴)王泰然（男）上海华东师大二附中金牌宣佩琦（男）浙扛绍兴一中金牌任宇翔（男）上海华东师大二附中金牌吕强（男）天津跃华中学金牌夏磊（男）北京四中金牌第23届(1992年，芬兰)陈涵（男）广东江门一中金牌“个人总成绩世界第一名”。

李翌（男）湖南师大附中金牌张霖涛（男）湖北江汉油田广华中学金牌石长春（男）河南开封高中金牌罗卫东（男）湖南沅扛一中金牌第24届（1993年，美国）张俊安（男）湖北沙市三中金牌“个人总成绩世界第一名”。

李林波（男）河南郑州一中金牌贾占峰（男）北京清华大学附中银牌韦韬（男）江苏南京师大附中银牌黄稚宁（男）湖南长沙一中铜牌第25届(1994年，中国)杨亮（男）上海华东师大二附中金牌“个人总成绩世界第一名”。