第八章组合变形构件的强度
- 格式:doc
- 大小:1.17 MB
- 文档页数:14


第八章 组合变形构件的强度8.1概 述到现在为止,我们所研究过的构件,只限于有一种基本变形的情况,例如拉伸(或压缩)、剪切、扭转和弯曲。
而在工程实际中的许多构件,往往存在两种或两种以上的基本变形。
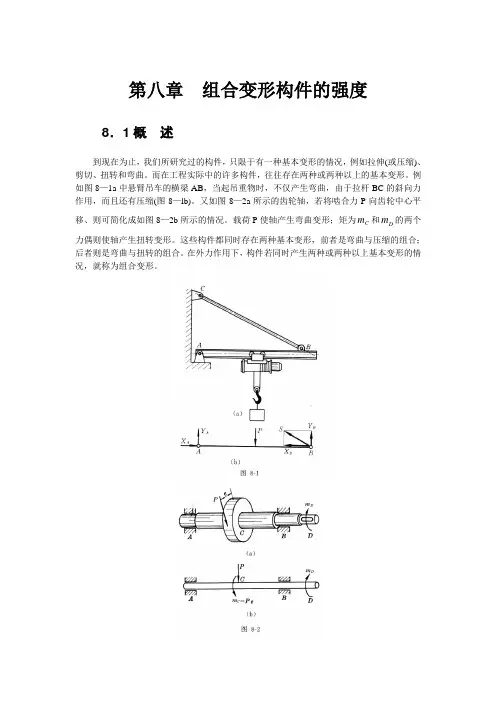
例如图8—1a 中悬臂吊车的横梁AB ,当起吊重物时,不仅产生弯曲,由于拉杆BC 的斜向力作用,而且还有压缩(图8—lb)。
又如图8—2a 所示的齿轮轴,若将啮合力P 向齿轮中心平移、则可简化成如图8—2b 所示的情况。
载荷P 使轴产生弯曲变形;矩为C m 和D m 的两个力偶则使轴产生扭转变形。
这些构件都同时存在两种基本变形,前者是弯曲与压缩的组合;后者则是弯曲与扭转的组合。
在外力作用下,构件若同时产生两种或两种以上基本变形的情况,就称为组合变形。
由于我们所研究的都是小变形构件,可以认为各载荷的作用彼此独立,互不影响,即任一载荷所引起的应力或变形不受其他载荷的影响。
因此,对组合变形构件进行强度计算,可以应用叠加原理,采取先分解而后综合的方法。
其基本步骤是:(1)将作用在构件上的载荷进行分解,得到与原载荷等效的几组载荷,使构件在每组载荷作用下,只产生一种基本变形;(2)分别计算构件在每种基本变形情况下的应力;(3)将各基本变形情况下的应力叠加,然后进行强度计算。
当构件危险点处于单向应力状态时,可将上述应力进行代数相加;若处于复杂应力状态,则需求出其主应力,按强度理论来进行强度计算。
本章将讨论弯曲与拉伸(或压缩)的组合以及弯曲与扭转的组合构件的强度问题。
8.2 弯曲与拉伸 (或压缩) 的组合在外力作用下,构件同时产生弯曲和拉伸(或压缩)变形的情况,称为弯曲与拉伸(或压缩)的组合变形。
图8—1所示悬臂吊的横梁同时受到横向载荷和纵向载荷的作用,这是弯曲与拉伸(或压缩)组合构件的一种受力情况。
在工程实际中,常常还遇到这样一种情况,即载荷与杆件的轴线平行,但不通过横截面的形心,此时,杆件的变形也是弯曲与拉伸(或压缩)的组合,这种情况通常称为偏心拉伸(或压缩)。


组合变形的强度计算 组合变形的概念拉伸与弯曲的组合一.组合变形的概念1.组合变形:在外力的作用下,构件若同时产生两种或两种以上基本变形的情况在小变形和线弹性的前提下,可以采用叠加原理研究组合变形问题所谓叠加原理是指若干个力作用下总的变形等于各个力单独作用下变形的总和(叠加)在复杂外载作用下,构件的变形会包含几种简单变形PRzxyPP2、组合变形的研究方法——叠加原理叠加原理应用的基本步骤:①外力分析:将载荷进行分解,得到与原载荷等效的几组载荷,使构件在每一组载荷的作用下,只产生一种基本变形.②内力分析:分析每种载荷的内力,确定危险截面.③应力分析:分别计算构件在每种基本变形情况下的危险将各基本变形情况下的应力叠加,确定最④强度计算:二.弯曲与拉伸(的组合杆件在外力作用下同时产生弯曲和拉伸(压缩)变形称为弯曲与拉伸(压缩)的组合偏心拉伸:弯曲与拉伸的组合变形链环受力立柱受力拉伸与弯曲组合的应力分析ϕϕsin p p cos p p y x ==A P x ='σy I M x l P M zy =''-=σ)(作用下:z T W M A N max max +=σzC W M A N max max -=σ危险截面处的弯矩抗弯截面模量y I M A N z +=''+'=σσσ根据叠加原理,可得x 横截面上的总应力为[]T z max max T W M A N σσ≤+=[]c zmax max C W M A N σσ≤-=强度条件为例:悬臂吊车,横梁由25 a 号工字钢制成,l =4m ,电葫芦重Q 1=4kN ,起重量Q2=20kN , α=30º, [σ]=100MPa,试校核强度。
取横梁AB为研究对象,受力如图b所示。
梁上载荷为P =Q1+Q2= 24kN,斜杆的拉力S 可分解为X B和Y B(1)外力计算横梁在横向力P和Y A、Y B作用下产生弯曲;同时在X A和X B作用下产生轴向压缩。



材料力学(土)笔记第八章 组合变形及连接部分的计算1.概 述工程实际中,构件在荷载作用下往往发生两种或两种以上的基本变形若几种变形所对应的应力(变形)属于同一数量级,则构件的变形成为组合变形对于组合变形下的构件,在线弹性、小变形条件下,可按构件的原始形状和尺寸进行计算 可先将荷载简化为符合基本变形外力作用条件的外力系分别计算构件在每一种基本变形下的内力、应力或变形利用叠加原理,综合考虑各基本变形的组合情况以确定构件的危险截面、危险点的位置及危险点的应力状态,并据此进行强度计算 若构件的组合变形超过了线弹性范围,或虽在线弹性范围内但变形较大则不能按其初始形状或尺寸进行计算,不能用叠加原理工程实际中,经常需要将构件相互连接铆钉、螺栓、键等起连接作用的部件,统称为连接件连接件(或构件连接处)的变形往往比较复杂,而其本身尺寸都比较小在工程设计中,通常按照连接的破坏可能性采用既能反映受力的基本特征,又能简化计算的假设,计算其名义应力然后根据直接试验的结果,确定其相应的许用应力,来进行强度计算这种简化计算的方法,称为工程实用计算法2.两相互垂直平面内的弯曲对于横截面具有对称轴的梁当横向外力或外力偶作用在梁的纵向对称面内时,梁发生对称弯曲 这是,梁变形后的轴线是一条位于外力所在平面内的平面曲线碰到双对称截面梁在水平和垂直两纵向对称平面内同时承受横向外力的作用情况这时梁分别在水平纵对称面(Oxz 平面)和铅垂纵对称面(Oxy 平面)内发生对称弯曲 在梁的任意横截面m-m 上,由1F 和2F 引起的弯矩值依次为1y M F x = 和 2()z M F x a =-梁的任一横截面m-m 上任一点(,)C y z 处与弯矩y M 和z M 相应的正应力分别为'yyM z I σ= 和 ''z z M y I σ=- 由叠加原理,在1F 和2F 同时作用下,截面m-m 上C 点处的正应力为 '''y z y z M M z y I I σσσ=+=-式中y I 和z I 分别为横截面对于两对称轴y 和z 的惯性矩y M 和z M 分别是截面上位于水平和铅垂对称平面内的弯矩且其力矩矢量分别与y 轴和z 轴的正向相一致在具体计算中,也可先不考虑弯矩和坐标的正负号,以其绝对值代入然后根据梁在荷载分别作用下的变形情况,判断由其引起该点处正应力的正负号为确定横截面上最大正应力点的位置,需求截面上中性轴的位置由于中性轴上各点处的正应力均为零,令0y 、0z 代表中性轴上任一点的坐标则由上式可得中性轴方程000yz yzM M z y I I -=由上式可见,中性轴是一条通过横截面形心的直线其与y 轴的夹角为θ,且tan tan y y z I I z M y M I I θϕ==⨯= 对于圆形、正方形等y z ,有由于梁各横截面上的合成弯矩M 所在平面的方位一般不相同所以,虽然每一截面的挠度都发生在该截面的合成弯矩所在平面内梁的挠曲线一般仍是一条空间曲线梁的挠曲线方程仍应分别按两垂直平面内的弯曲来计算,不能直接用合成弯矩计算 确定中性轴位置后,作平行于中性轴的两条直线,分别与横截面周边相切于两点该两点即分别为横截面上拉应力和压应力为最大的点对于工程中常用的矩形、工字型等截面梁其横截面都有都有两个互相垂直的对称轴,且截面的周边具有棱角故横截面上的最大正应力必发生在截面的棱角处于是,可根据梁的变形情况,直接确定截面上最大拉、压应力点的位置,无需定出中性轴 在确定了梁的危险截面和危险点的位置,并算出危险点处的最大正应力之后由于危险点处于单轴应力状态,可按正应力强度条件计算横截面上的切应力,对于一般实体截面梁,其数值较小,可不必考虑3.拉伸(压缩)与弯曲3.1 横向力与轴向力共同作用等直杆受横向力和轴向力共同作用时,杆将发生弯曲与拉伸(压缩)组合变形对于弯曲刚度EI 较大的杆,由于横向力引起的挠度与横截面的尺寸相比很小因此,由轴向力在相应挠度上引起的弯矩可略去不计可分别计算由横向力和轴向力引起的杆横截面上的正应力按叠加原理求其代数和,即得在组合变形下,杆横截面上的正应力max ,max N t t b F M A Wσσσ=+=+ 当材料的许用拉应力和许用压应力不相等时杆内的最大拉应力和最大压应力必须分别满足杆件的拉、压强度条件对于弯曲刚度EI 较小的杆件,在压缩和弯曲组合变形下轴向压力引起的附加弯矩较大,且其转向与横向力引起的弯矩相同因此不能按杆的原始形状来计算,叠加原理也不再适用3.2 偏心拉伸(压缩)作用在直杆上的外力,当其作用线与杆的轴线平行但不重合时,将引起偏心拉伸或偏心压缩 横截面具有两对称轴的等直杆承受矩截面形心为e (称为偏心距)的偏心拉力F 为例 先将作用在杆端截面上A 点处的拉力F 向截面形心1O 点简化得到轴向拉力F 和力偶矩Fe ,将力偶矩分解为ey M 和ez Msin ey F M Fe Fz α==cos ez F M Fe Fy α==式中,坐标轴y 、z 为截面的两个对称轴F y 、F z 为偏心拉力F 作用点(A 点)的坐标于是的得到一个包含轴向拉力和两个在纵对称面内的力偶的静力等效力系此力系将分别使杆发生轴向拉伸和在两相互垂直的纵对称面内的纯弯曲当杆的弯曲刚度较大时,同样可按叠加原理求解在上述力系作用下任一横截面n-n 上的任一点(,)C y z 处相应于轴力N F F =和两个弯矩的正应力,由叠加原理,的C 点处的正应力F F y zFz z Fy y F A I I σ⨯⨯=++ 利用惯性矩与惯性半径间的关系 2y yI A i =⨯,2z z I A i =⨯ 式子可改写为22(1)FF y zz z y y F A i i σ=++ 上式是一个平面方程,表明正应力在横截面上按线性规律变化应力平面与横截面相交的直线(沿该直线0σ=)就是中性轴令0y 、0z 代表中性轴上任一点的坐标,代入即得中性轴方程002210F F y z z y z y i i ++= 在偏心拉伸(压缩)情况下,中性轴是一条不通过截面形心的直线为定出中性轴的位置,可利用其在y 、z 两轴上的截距y a 和z a在上式中,令00z =,相应的0y 即为截距y a ,而令00y =,相应的0z 即为截距z a 由此求得2z y F i a y =-,2y z Fi a z =- A 在第一象限内,F y 、F z 都为正值,则y a 、z a 均为负值即中性轴与外力作用点分别处于截面形心的相对两侧对于周边无棱角的截面,可作两条与中性轴平行的直线与横截面的周边相切两切点即为横街面上最大拉应力和最大压应力所在的危险点将危险点的坐标代入公式即可求得最大拉应力和最大压应力对于周边具有棱角的截面,其危险点必定在截面的棱角处,并可根据杆件的变形来确定 最大拉应力,max t σ和最大压应力,max c σ,其值为,max ,max t F F c yz Fz Fy F A W W σσ⎫⎪=±±⎬⎪⎭ 式子对箱型、工字形等具有棱角的截面都适用当外力的偏心距(F y 、F z )较小时,中性轴可能不与横截面相交即横截面就可能不出现与轴力异号的应力由于危险点仍处于单轴应力状态,可按正应力的强度条件进行计算3.3 截面核心如前所述,当偏心轴向力F 的偏心距较小时,杆横截面上就可能不出现异号应力 因此当偏心压力F 的偏心距较小时,杆的横截面上可能不出现拉应力外力作用点离形心越近,中性轴距形心就越远当外力作用点位于截面形心附近的一个区域内时,就可以保证中性轴不与横截面相交,这个区域就称为截面核心当外力作用在截面核心的边界上时相对应的中性轴正好与截面的周边相切,利用这一关系就可确定截面核心的边界为确定任意形状截面的截面核心边界,可将与截面周边相切的任一直线视作中性轴 在y 和z 形心主惯性轴上的截距分别为1y a 和1z a可确定与该中性轴对应的外力作用点1按上述方法求得与其对应的截面核心边界上的点2、3、…的坐标连接这些点所得到的一条封闭曲线,即为所求截面核心的边界该边界曲线所包围的带阴影线的区域,即为截面核心圆截面对于圆心O 时极对称的,因此,截面核心的边界对于圆心也是极对称的为一圆心为O 的圆作一条与圆截面周边相切于A 点的直线,将其视为中性轴取OA 为y 轴,于是,该中性轴在y 和z 形心主惯性轴上的截距为1/2y a d =, 1z a =∞圆截面的222/16y z i i d ==,将其代入公式即得与其对应的截面核心边界上点1的坐标2211/16/28z y y i d d a d ρ=-=-=-,2110y z z i a ρ=-= 从而可知,截面核心边界是一个以O 为圆心,/8d 为半径的圆对于边长为b h ⨯的矩形截面,两对称轴y 和z 为截面的形心主惯性轴将与AB 向切的直线①视作中性轴,其在y 和z 轴上的截距分别为,矩形截面2212yb i =,2212z h i = 将上式代入,即得中性轴①对应的截面核心边界点上点1的坐标为2211/12/26z y y i h h a h ρ=-=-=-, 2110y z z i a ρ=-= 同理,分别将与矩形边界相切的直线②、③、④视作中性轴可得对应的截面核心边界上点2、3、4的坐标从而得到了截面核心边界上的4个点当中性轴从截面的一个侧边绕截面的顶点旋转到其相邻边时 将得到一系列通过边界点B 但斜率不同的中性轴而B 点的坐标(,)B B y z 是一系列中性轴共有的 将其代入中性轴方程,经改写后得2222110F F B B B B F F y z y z z y z y z y z y i i i i ++=++= 上式中,B y 、B z 为常数 因此该式就可看作时表示外力作用点坐标(,)F F y z 间关系的直线方程即当中性轴绕B 点旋转时,相应的外力作用点移动的轨迹是一条连接点1、2的直线将1、2、3、4四点中相邻的两点连以直线,即得矩形截面的截面核心边界截面核心为位于截面中央的菱形对于具有棱角的截面,均可按照上述方法确定其截面核心对于周边有凹进部分的截面(例如槽型或T 字型截面等)在确定截面核心边界时,应该注意不能取与凹进部分的周边相切的直线作为中性轴,因为这种直线显然约横截面相交4.扭转与弯曲一般的传动轴通常发生扭转与弯曲组合变形讨论杆件发生扭转与弯曲组合变形时的强度计算直径为d 的等直圆杆AB ,A 端固定,B 端具有与AB 成直角的刚臂,并受铅垂力F 作用,将F 简化为一作用于杆端截面形心的横向力F 和一作用于杆端的力偶矩e M Fa = 杆AB 将发生弯曲与扭转组合变形分别作杆的弯矩图和扭矩图,可见杆的危险截面为固定端截面,内力分量分别为M Fl =, e T M Fa ==由弯曲和扭转的应力变化规律可知危险截面上的最大弯曲正应力σ发生在铅垂直径的上、下两端点对于许用拉应力,压应力相等的塑性材料来说,该两点的危险程度相同 研究任一点,围绕该点分别用横截面、径向纵截面和切向纵截面截取单元体 该点应力状态如图所示,可见该点处于平面应力状态,其三个主应力为132σσσ⎫=⎬⎭ 20σ= 对于塑性材料制成的杆件,选用第三或第四强度理论来建立强度条件用第三、第四强度理论,将上述各应力代入向相应的应力表达式求得相当应力后,即可根据材料的许用应力[]σ来建立强度条件,对杆进行强度计算 其中弯曲正应力/M W σ=,扭转切应力/p T W τ=,对于圆截面杆2p W W =截面周边各点处弯曲正应力的数值和正负号都将随着轴的转动而交替变化这种应力称为交变应力,交变应力下工作的构件另有相应的计算准则5.连接件的实用计算法5.1 剪切的实用计算设两块钢板用螺栓连接后承受拉力F螺栓在两侧面上分别收到大小相等、反向相反、作用线相距很近的两组分布力系的作用 螺栓在这样的作用下,将沿两侧外力之间,并与外力作用线平行的截面m-m 发生相对错动称为剪切面应用截面法,可得剪切面上的内力,即剪力s F在剪切实用计算中,假设剪切面上各点处的切应力相等 于是剪切面上的名义切应力为S sF A τ=式中s A 为剪切面面积,s F 为剪切面上的剪力 通过试验得到剪切破坏时材料的极限切应力u τ,除以安全因数,得许用应力[]τ 剪切强度表示为[]S sF A ττ=≤ 名义切应力并不反映剪切面上切应力的精确理论值只是剪切平面上的平均切应力但对于低碳钢等塑性材料材料制成的连接件,变形较大而临近破坏时剪切面上的切应力将逐渐趋于均匀而且满足剪切强度条件式,不至于发生剪切破坏,从而满足工程需要对于大多数的连接件来说,剪切变形及剪切强度时主要的5.2 挤压的实用计算螺栓连接中,在螺栓与钢板相互接触的侧面上,将发生彼此间的局部承压现象,称为挤压 在接触面上的压力,称为挤压力,并记为bs F挤压力可根据被连接件所受的外力,由静力平衡条件求得当挤压力过大时,可能引起螺栓压扁或钢板在孔缘压皱,从而导致连接松动失效在挤压实用计算中,假设名义挤压应力的计算式为bs bs bsF A σ= 式中,bs F 为接触面上的挤压力;bs A 为计算挤压面面积当接触面为圆柱面时,计算挤压面面积bs A 取为实际接触面在直径平面上的投影面积 理论表明,这类圆柱状连接件与钢板孔壁间接触面上的理论挤压应力沿圆柱的变化情况如图 计算所得的名义挤压应力与接触面中点处的最大理论挤压应力值相近当连接件与被连接构件的接触面为平面时,计算挤压面面积即为实际接触面的面积 通过试验,按名义挤压应力公式得到的材料的极限挤压应力,除以安全因数确定许用挤压应力[]bs σ,则挤压强度条件可表达为[]bs bs bs bsF A σσ=≤ 注意,挤压应力是在连接件和被连接件之间相互作用的当两者材料不同时,应校核其中许用挤压应力较低的材料的挤压强度6.铆钉连接的计算铆钉连接在建筑结构中被广泛采用铆接的方式主要有搭接、单盖板对接和双盖板对接三种搭接和单盖板对接中的铆钉具有一个剪切面(称为单剪)双盖板对接中的铆钉具有两个剪切面(称为双剪)6.1 铆钉组承受横向荷载在搭接和单盖板对接中,由铆钉的受力可见铆钉(或钢板)显然将发生弯曲在铆钉组连接中,在弹性变形阶段两端铆钉的受力与中间铆钉的受力并不完全相同 为简化计算,并考虑到连接在破坏前将发生塑性变形,在铆钉计算中假设①不论铆接的方式如如何,均不考虑弯曲的影响②若外力的作用线通过铆钉组横截面的形心,且同一组内各铆钉的材料与直径均相同,则每个铆钉的受力相等 按照上述假设,即可得每个铆钉的受力1F 为1F F n= 式中,n 为铆钉组中的铆钉数求得每个铆钉的受力1F 后,即可分别校核其剪切强度和挤压强度被连接件由于铆钉孔的削弱,其拉伸强度应以最弱截面(轴力较大,截面积较小)为依据 不考虑集中应力的影响对于销钉或螺栓连接,其分析计算方法与铆钉连接相同6.2 铆钉组承受扭转荷载承受扭转荷载的铆钉组,由于被连接件(钢板)的转动趋势每一铆钉的受力将不再相同令铆钉组横截面形心为O 点 假设钢板的变形不计,可视为刚体于是,每一铆钉的平均切应变与该铆钉截面中心至O 点的距离成正比,其方向垂直于该点与O 点的连线由合力矩定理,每一铆钉上的力对O 点力矩的代数和等于钢板所受的扭转力偶矩e M ,即 e i i M Fe Fa ==∑式中,i F 为铆钉i 所受的力;i a 为该铆钉截面中心至铆钉组截面形心的距离对于承受偏心横向荷载的铆钉组可将偏心荷载F 向铆钉组截面形心O 简化得到一个通过O 点的荷载F 和一个绕O 点旋转的扭转力偶矩e M Fe =若同一铆钉组中每一铆钉的材料和直径均相同则可分别计算由力F 引起的力'i F 和由转矩e M 引起的力''i F铆钉i 的受力为'i F 和''i F 的矢量和求得铆钉i 的受力i F 后,可分别校核受力最大的铆钉的剪切强度和挤压强度。


第八章 组合变形判断 拉弯组合1、“斜弯曲时中性轴一定过截面的形心而且中性轴上的正应力为零。
”2、“当载荷不在梁的主惯性平面内,梁一定产生斜弯曲”3、“拉弯组合变形时,中性轴一定不过截面的形心”4、“杆件发生斜弯曲时,杆件变形的总挠度方向一定与中性轴相垂直。
”5、“只要杆件横截面上的轴力为零,则该横截面上的正应力各处为零”6、“承受偏心拉伸的杆件,其中性轴仍然通过截面的形心”7、“拉弯组合变形和偏心拉伸组合变形的中性轴位置都与载荷的大小无关。
”选择 拉弯组合1、应用叠加原理的前提条件是: 。
A :线弹性构件; B :小变形杆件;C :线弹性、小变形杆件;D :线弹性、小变形、直杆; 2、矩形截面偏心受压杆件发生 变形。
A :轴向压缩、平面弯曲B :轴向压缩、平面弯曲、扭转 C:轴向压缩、斜弯曲 D :轴向压缩、斜弯曲、扭转3、平板上边切h/5,在下边对应切去h/5,平板的强度。
A :降低一半;B :降低不到一半;C :不变;D :提高了;4、AB 杆的A 处靠在光滑的墙上,B 端铰支,在自重作用下发生变形, AB 杆发生 变形。
A :平面弯曲B :斜弯;C :拉弯组合;D :压弯组合;5、简支梁受力如图:梁上 。
A :AC 段发生弯曲变形、CB 段发生拉弯组合变形 B :AC 段发生压弯组合变形、CB 段发生弯曲变形C :两段只发生弯曲变形D :AC 段发生压弯组合、CB 段发生拉弯组合变形6、图示中铸铁制成的压力机立柱的截面中,最合理的是 。
7、矩形截面悬臂梁在自由端受到力P 的作用,如图。
OP 为载荷的作用线,已知I Z <I Y 。
则该梁横截面的 。
A :中性轴位于1、3象限,挠度方向可能为Of 1 B :中性轴位于1、3象限,挠度方向可能为Of 2C :中性轴位于2、4象限,挠度方向可能为Of 1D :中性轴位于2、4象限,挠度方向可能为Of 28、矩形截面拉弯组合变形时,对于横截面的中性轴有以下的结论。
第八章 组合变形构件的强度8.1概 述到现在为止,我们所研究过的构件,只限于有一种基本变形的情况,例如拉伸(或压缩)、剪切、扭转和弯曲。
而在工程实际中的许多构件,往往存在两种或两种以上的基本变形。
例如图8—1a 中悬臂吊车的横梁AB ,当起吊重物时,不仅产生弯曲,由于拉杆BC 的斜向力作用,而且还有压缩(图8—lb)。
又如图8—2a 所示的齿轮轴,若将啮合力P 向齿轮中心平移、则可简化成如图8—2b 所示的情况。
载荷P 使轴产生弯曲变形;矩为C m 和D m 的两个力偶则使轴产生扭转变形。
这些构件都同时存在两种基本变形,前者是弯曲与压缩的组合;后者则是弯曲与扭转的组合。
在外力作用下,构件若同时产生两种或两种以上基本变形的情况,就称为组合变形。
由于我们所研究的都是小变形构件,可以认为各载荷的作用彼此独立,互不影响,即任一载荷所引起的应力或变形不受其他载荷的影响。
因此,对组合变形构件进行强度计算,可以应用叠加原理,采取先分解而后综合的方法。
其基本步骤是:(1)将作用在构件上的载荷进行分解,得到与原载荷等效的几组载荷,使构件在每组载荷作用下,只产生一种基本变形;(2)分别计算构件在每种基本变形情况下的应力;(3)将各基本变形情况下的应力叠加,然后进行强度计算。
当构件危险点处于单向应力状态时,可将上述应力进行代数相加;若处于复杂应力状态,则需求出其主应力,按强度理论来进行强度计算。
本章将讨论弯曲与拉伸(或压缩)的组合以及弯曲与扭转的组合构件的强度问题。
8.2 弯曲与拉伸 (或压缩) 的组合在外力作用下,构件同时产生弯曲和拉伸(或压缩)变形的情况,称为弯曲与拉伸(或压缩)的组合变形。
图8—1所示悬臂吊的横梁同时受到横向载荷和纵向载荷的作用,这是弯曲与拉伸(或压缩)组合构件的一种受力情况。
在工程实际中,常常还遇到这样一种情况,即载荷与杆件的轴线平行,但不通过横截面的形心,此时,杆件的变形也是弯曲与拉伸(或压缩)的组合,这种情况通常称为偏心拉伸(或压缩)。
载荷的作用线至横截面形心的垂直距离称为偏心距。
例如图8—3a 中的开口链环和图8—4a 中的厂房柱子,如果将其上的载荷P 向杆件横截面的形心平移,则作用于杆件上的外力可视为两部分:一个轴向力P 和一个矩为Pe M =0 的力偶(图8—3b 、8—4b)。
轴向力P 将使杆件产生轴向拉伸(或压缩);力偶将使杆件产生弯曲。
由此可见,偏心拉伸(或压缩)实际上就是弯曲与拉伸(或压缩)的组合变形。
现在讨论弯曲与拉伸(或压缩)组合变形构件的应力和强度计算。
设一矩形截面杆,一端固定,一端自由(图8—5a),作用于自由端的集中力P 位于杆的纵对称面Oxy 内,并与杆的轴线x 成一夹角ϕ。
将外力P 沿x 轴和y 轴方向分解,得到两个分力(图8—5b):ϕcos P P x = ϕsin P P y =其中,分力x P 为轴向外力,在此力的单独作用下,杆将产生轴向拉伸,此时,任一横截面上的轴力x P N =。
因此,杆横截面上各点将产生数值相等的拉应力,其值为AN ='σ 正应力'σ在横截面上均匀分布,如图8—5c 所示。
分力y P 为垂直于杆轴线的横向外力,在此力的单独作用下,杆将在Oxy 平面内发生平面弯曲,任一横截面的弯矩为)(x l P M y -= 此时在横截面上任一点K 的弯曲应力为ZI My=''σ ''σ沿截面高度方向的变化规律,如图8—5d 所示。
由此可见,这是一个弯曲与拉伸组合变形的杆件。
设在外力作用下杆件的变形很小,这时可应用叠加原理,将拉伸正应力'σ与弯曲正应力''σ按代数值叠加后,得到横截面上的总应力为IMyA N +=+='''σσσ ( 8—1 ) 设横截面上、下边缘处的最大弯曲应力大于(或小于)拉伸正应力,则总应力σ沿截面高度方向的变化规律如图8—5e(或8—5f)所示。
由于在固定端处横截面上的弯矩最大,因此,该截面为危险截面。
从图8—5e 可知,构件的危险点位于危险截面的上边缘或下边缘处。
在下边缘处由于'σ和''σ均为拉应力,故总应力为两者之和,由此得最大拉应力为Zt W M A N maxmax +=σ ( 8—2 ) 在上边缘,由于'σ为拉应力,而''σ为压应力,.故总应力为两者之差,由此得最大压应力为Zc W M A N max max -=σ ( 8—3 ) 上两式中的m ax M 为危险截面处的弯矩;。
Z W 为抗弯截面系数。
得到了危险点处的总应力后,即可根据材料的许用应力建立强度条件: []t Z t W M A N σσ≤+=maxmax ( 8—4 ) []c Zc W M A N σσ≤-=maxmax ( 8—5 ) 式中[]t σ和[]c σ分别为材料拉伸和压缩时的许用应力。
一般情况下,对于抗拉与抗压能力不相等的材料,如铸铁和混凝土等,需用以上两式分别校核构件的强度;对于抗拉与抗压能力相等的材料,如低碳钢,则只需校核构件应力绝对值最大处的强度即可。
对于偏心拉伸的杆件,上述公式仍然成立,只须将式中的最大弯矩m ax M 改为因载荷偏心而产生的弯矩Pe M =即可。
若外力P 的轴向分力x P 为压力或偏心压缩时,上述公式中的第一项AN则应取负号。
还应指出,在上面的分析中,对于受横向力作用的杆件,横截面上除有正应力外,还有因剪力而产生的切应力,必要时还需考虑切应力的强度。
例8—1 悬臂吊车如图8—6a 所示,横梁用25a 号工字钢制成,梁长l =4m ,斜杆与横梁的夹角 30=α,电葫芦重1Q =4kN ,起重量2Q =20kN ,材料的许用应力[]σ=100MPa 。
试校核横梁的强度。
解:(1)外力计算 取横梁AB 为研究对象,其受力图如图8—6b 所示。
梁上载荷为KN Q Q P 2421=+=,右端斜杆的拉力S 可分解为B X 、B Y 两个分力。
横梁在横向力P 和A Y 、BY 作用下产生弯曲;同时在A X 和B X 作用下产生轴向压缩。
这是一个弯曲与压缩组合的构件。
当载荷移动到梁的中点时,可近似地认为梁处于危险状态。
此时,由平衡条件∑=0A M , 02=•-lP l Y B 得KN PY B 122==而KN Y X B B 8.20577.01230tan ===又由平衡条件∑=0Y 和∑=0X ,得:KN Y A 12=KN X A 8.20=(2)内力和应力计算 根据横梁的受力情形,和上面求得的数值,可以绘出横梁的弯矩图如图8—6c 所示。
在梁中点截面上的弯矩最大,其值为m N Pl M •=⨯==2400044240004max 从型钢表上查得25a 号工字钢的截面面积和抗弯截面系数分别为: 242105.485.48m cm A -⨯== 36210402402m cm W Z -⨯==所以最大弯曲应力为MPa Pa W M Z B 60107.59104022400066max max ≈⨯≈⨯==-σ 其分布如图8—6e 所示,梁危险截面的上边缘处受最大压应力、下边缘处受最大拉应力作用。
横梁所受的轴向压力为 B X N =则危险截面上的压应力为MPa Pa A X A N B c 29.41029.400485.0208006-=⨯-=-=-=-=σ 并均匀分布于横截面上,如图8—6d 所示。
故梁中点横截面上、下边缘处的总正应力分别为(图8—6f):MPa W M A N Z c 3.646029.4maxmax -≈--=--=σMPa W M A N Zt 7.556029.4max max ≈+-=+-=σ (3)强度校核 曲于工字钢的抗拉与抗压能力相同,故只校核正应力绝 对值最大处的强度即可,即[]σσ<=MPa c 64max由计算可知,此悬臂吊车的横梁是安全的、例-8-2 图8—7a 所示的钻床,钻孔时受到压力P=15kN 。
已知偏心矩e =40cm ,铸铁立柱,的许用拉应力[]t σ=35MPa ,许用压应力[]c σ=120MPa ,试计算铸铁立柱所需的直径。
解:(1)计算内力立柱在力P 作用下产生偏心拉伸-,将立柱假想地截开,取上段为研究对象(图8-7b),由平衡条件,不难求得立柱的轴力和弯矩分别为: N P N 15000==m N Pe M •=⨯==60004.015000(2)选择立柱直径 由于铸铁的许用拉应力[]t σ小手许用压应力[]c σ,因此,应根据最大拉应力m ax t σ来进行强度计算。
由公式(8—4),[]t Zt W Pe A N σσ≤+=max 得6321035326000415000⨯≤+d d ππ 解此方程就能得到立柱的直径d 。
但因这是一个三次方程,求解较繁。
因此,在设计计算中常采用一种简便的方法。
一般在偏心距较大的情况下,偏心拉伸(或压缩)杆件的弯曲正应力是主要的,所以可先按弯曲强度条件求出立柱的一个近似直径,然后将此直径的数值稍微增大,再代入偏心拉伸的强度 条件(式8—4)中进行校核,如数值相差较大,再作调整,如此逐步逼近,最后可求得满足此方程的直径。
在此题中,先考虑弯曲强度条件[]σ≤ZW M即63103532326000⨯≤d π 由此解得立柱的近似直径m d 12.0=将其稍加增大,现取m d 12.0=,再代入偏心拉伸的强度条件校核,得[]MPa MPa t 355.32105.3232125.014.360004125.014.315000622max =<=⨯=⨯+⨯=σσ 满足强度条件,最后选用立柱直径m d 125.0=。
例8—3 一带槽钢板受力如图8—8a 所示,已知钢板宽度b =8cm ,厚度δ=1cm ,边缘上半圆形槽 的半径r =lcm ,已知拉力P =80kN ,钢板许用应力[]σ=140MPa 。
试对此钢板进行强度校核。
解:由于钢板在截面I--I 处有一半圆槽,因而外力P 对此截面为偏心拉伸,其偏心距之值为cm r r b b e 5.021222===--=截面I--I 处的轴力和弯矩分别为: N KN P N 8000080===m N Pe M •=⨯==400005.080000轴力N 和弯矩M 在半圆槽底部的。
点处都引起拉应力(图8—8b),此处即为危险点。
由式(8—4)得最大拉应力为[]σδδσ>=⨯=-⨯⨯+-⨯=-+-=MPa Pa r b Pe r b P t 3.163103.163)01.008.0(01.04006)01.008.0(01.0800006)()(622max计算结果表明,钢板在截面I--I 处的强度不够。