平面简谐波的波函数(知识题课)

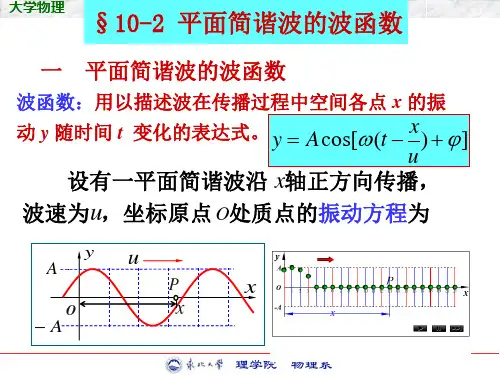
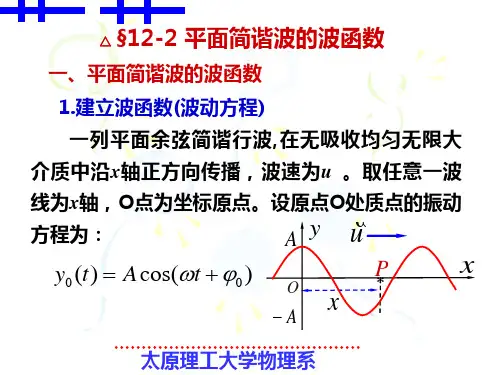
第二讲 平面简谐波的波函数例：横波波形y x uA A -O Px如图，向x 轴正向传播的一列平面简谐波某时刻的波形P 点振动落后于O 点振动，落后的时间为 P 点振动落后于O点振动，落后的位相为x P λπϕϕϕ2O =-=∆ux t t t P =-=∆O()ϕω+=t A y O cos y x uA A -O PxO 点作简谐振动，振动方程为 P 点也作简谐振动，振动方程为()[]⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=+-=-=φu x t ωA φt t ωA t t y y O P cos Δcos )Δ( 或者为[]⎤⎡-+=∆-+=x φωt A φωt A y P πϕ2cos cos由于P 为波传播方向上任一点，因此上述方程能描述波传播方向上任一点的振动，具有一般意义，即为沿 x 轴正方向传播的平面简谐波的波函数，又称波动方程。

利用 和 ，可以证明上述两个方程是完全一样的。

νT π2π2==ωuT =λ波函数⎥⎦⎤⎢⎣⎡-+=+-=x t A u x t A y λπϕωϕω2cos ])(cos[质元的振动速度，加速度])(sin[ϕωω+--=∂∂=ux t A t y v y ux t A t y a 2222-])(cos[ωϕωω=+--=∂∂=二 波函数的物理含义（波具有时间的周期),(),(T t x y t x y +=()ϕω'+=t A y cos 则ϕλϕ+-='x π2令⎪⎭⎫ ⎝⎛+-=ϕλωx t A y π2cos O y t1 一定， 变化x t 表示 点处质点的振动方程（ 的关系）ty —x波线上各点的简谐运动图C t =+=''ϕωϕ令（定值）⎥⎦⎤⎢⎣⎡''+-=ϕλx A y π2cos 则 y ⎪⎭⎫ ⎝⎛-+=λϕωx t A y π2cos 2 一定 变化x t 该方程表示 t 时刻波传播方向上各质点的位移, 即 t 时刻的波形（ y-x 的关系）方程表示在不同时刻各质点的位移，即不同时刻的波形，体现了波的传播.y xuO 3 、 都变x t()ϕω+=t A yOcos y xuAA -OPx如图，设O 点振动方程为u xt =Δ P 点振动比O 点超前了 ,4 沿 轴方向传播的波动方程 x-从形式上看：波动是波形的传播.从实质上看：波动是振动的传播. 故 P 点的振动方程（波动方程）为：])(cos[)(ϕω++=∆+=uxt A t t y y o 同样也可以表示为：⎥⎦⎤⎢⎣⎡++=x t A y λπϕω2cos例1 一平面简谐波沿 Ox 轴正方向传播， 已知振幅 A=1.0m ,T=2.0s, λ=2.0m. 在t=0 时坐标原点处的质点在平衡位置沿 Oy 轴正向运动. 求 ： (1)波动方程； (2) t=1.0s 时的波形图；（3）x=0.5m 处质点的振动规律并作图解 (1) 写出波动方程的标准式])(π2cos[ϕλ+-=xT t A y2π-=ϕ0,0>∂∂==t y y v 0==x t ])(π2cos[ϕλ+-=xT t A y yωAO]2π)0.20.2(π2cos[--=x t y (m)利用初始条件，(2)求 波形图s0.1=t ]π2πcos[0.1x y -=波形方程s0.1=t 0m/y m/x 2.01.0-1.0时刻波形图s0.1=t ]2π)0.20.2(π2cos[0.1--=x t y x πsin =(m)由(3) 处质点的振动规律并作图 m5.0=x ]2π)0.20.2(π2cos[)0.1(--=x t y 处质点的振动方程m 5.0=x ]πcos[π-=t y (m)0m/y 1.0-1.0s /t 2.0O yω******123412341.0由得例2 一平面简谐波以速度u=20m · s -1沿直线传播，波线上点 A 的简谐运动方 程是y=3 × 10-2cos(4πt), (y, t 的单位分别是m ，s ）求:(1)以 A 为坐标原点，写出波动方程；(2)以 B 为坐标原点，写出波动方程；(3)求传播方向上点C 、D 的简谐运动方程；(4)分别求出 BC ，CD 两点间的相位差.uAB CD5 m9 mxo 8 m(1) 以 A 为坐标原点，写出波动方程m10==uT λm1032-⨯=A s5.0=T 0=ϕ)105.0(π2cos 1032x t y -⨯=-])(π2cos[ϕλ+-=xT t A y uAB CD5 m9 mxo 8 m 利用得πλϕϕ==-BA AB x x -π2]ππ4cos[1032+⨯=-t y B ]π)105.0(π2cos[1032+-⨯=-xt y (2) 以 B 为坐标原点，写出波动方程uABCD5 m9 m xo 8 m B 点的振动比 A 点超前，所以，φB =π。

第一讲平面简谐波函数内容提要
1.波动的几个概念
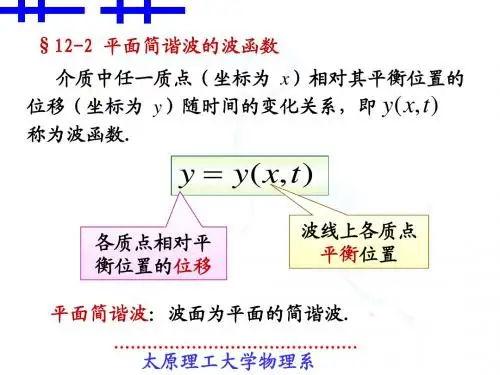
2.平面简谐波函数
3.波函数的物理意义
4.举例
波源
+弹性作用介质
质元的振动状态将在较晚时刻于“下游”某---波是振动状态的传播。

点----质元的振动状态相同。

1=ν
λu 速：波动过程中，某一振动状态（即）单位时间内所传播的距离（相速）.u
O 落后的相位O p ϕϕϕ−=∆λx
π
2−=
x
,0==ϕx 相位落后法
x
)
cos(),(ϕω+−=kx t A t x λ
π
2=
k 角波数速度，加速度
]
)(sin[ϕωω+−−=∂=x t A y
（波具有空间的周期性）
),(t x y λ+
般步骤
并明确波的传播方向。

点的位置，写出其振动方程。

x处的任一点和参考点（振源
−
−−t x t )2.50s [(π])cm 01.0()2.50s -1
1-1-1π
2])2=
x
cos[y A t ω=+
t
=
s0.1
)
(cos u
t −−ω为为正常数，求波长、波速、波传播方的两点间的相位差.
)cos(Cx Bt A y −=C B ,d λ
x
t )
π,(=ϕ向x 轴负向传播
t=T/4 t =0。