当前位置：文档之家 › 二自由度振动有阻尼及强迫振动响应

二自由度振动有阻尼及强迫振动响应

  • 格式：pdf
  • 大小：659.84 KB
  • 文档页数：16

下载文档原格式

  / 16

合集下载

简谐激励下强迫振动的响应特性-57页文档资料

简谐激励下强迫振动的响应特性-57页文档资料

k o Fk
Δ
x
c
F Fc
m
mg
Solution
The equation of motion: 5 x 2 0 0 0 x 1 0 s in 2 0 t
n
2000 20 rad/s 5
例 （1）
Particular solution:
x 2 t tc 1 c2 o t c 0 s 2 s2 itn 0
简谐激励下强迫振动的响应特性
强迫振动的几种形式
强迫振动的运动方程
单自由度运动微分方程的一般形式
取不同形式时，振动特点不同
其中简谐激励为最简单的激励形式
简谐激励下的响应
运动微分方程的解
x(t)xh(t)xp(t)
其中, x h (t) 为相应齐次方程的解
瞬态响应
（有阻尼系统中该项解将逐渐消失）
运动方程一般形式 假设稳态解形式并代入运动方程得
用三角函数公式展开 令两边同谐波项相等
幅频特性 相频特性
无量纲化
式中：
振幅放大系数（幅值比）
力函数和响应相位差
稳态响应的相位特性
Force Excitation
F(t) Restoring
kx
Damping
cx
Inertia
m x 2
Amplitude F0
F
c
m
mg
Substitute above equations in equation of motion to obtain
2 c 1 s 0 2 t i c 2 0 c n 0 2 t o 2 0 t c 1 s c 0 2 t o c 0 2 s 0 2 t s i 0 2 n 0 t c 1 c 0 2 t o c 0 2 s 0 2 t s i 0

阻尼振动与强迫振动的区别与联系

阻尼振动与强迫振动的区别与联系

阻尼振动与强迫振动的区别与联系引言：振动现象广泛存在于自然界和工程领域中。

阻尼振动和强迫振动作为振动现象的两种基本形式，它们在物理特性、引起原因和动力学特征等方面存在一定的区别和联系。

本文将着重讨论阻尼振动与强迫振动的区别与联系，以深入了解这两种振动形式的本质。

一、阻尼振动的定义与特点阻尼振动是指受到阻尼力作用下的振动现象。

在阻尼振动中，振动系统受到阻尼力的耗散作用，会导致振幅的逐渐减小，直至 eventually下降为零。

阻尼振动的物理特性主要包括振动频率的减小、振幅的衰减和振动系统能量的损失。

二、强迫振动的定义与特点强迫振动是指在外界作用下，振动系统受到周期性或非周期性的外力驱动，并由此产生的振动现象。

与阻尼振动不同，强迫振动在无外力驱动时不会自发发生。

强迫振动的物理特性主要包括受迫振动频率与外力频率的一致性、振幅的稳定性和外界驱动力对振动系统的影响。

三、阻尼振动与强迫振动的区别1. 物理特性：阻尼振动主要表现为能量的衰减和振幅的逐渐减小，而强迫振动的振幅较为稳定，受迫振动频率与外力频率一致。

2. 引起原因：阻尼振动产生的主要原因是振动系统与环境介质之间的相互作用，而强迫振动则是由外界施加的外力引起的。

3. 频率依赖性：阻尼振动的频率与外界没有直接的关系，而强迫振动的频率受外界驱动力的影响，与外力频率保持一定的一致性。

4. 能量耗散：阻尼振动会因阻尼力的作用逐渐损失能量，而强迫振动的振动系统能量主要来自外界驱动力。

四、阻尼振动与强迫振动的联系1. 泛化关系：强迫振动可以看作是阻尼振动的一种特殊情况，当外界驱动力的频率趋近于阻尼振动系统的固有频率时，强迫振动会逐渐趋近于稳定状态。

2. 共存关系：在实际物理系统中，阻尼振动与强迫振动可以同时存在。

外界施加的强迫力可能使阻尼振动系统产生共振现象，引起系统的不稳定性。

3. 相互影响：阻尼振动和强迫振动之间存在着相互影响关系。

阻尼振动的存在会导致强迫振动的振幅逐渐减小，而强迫振动的存在也会影响阻尼振动系统的能量耗散。

机械动力学第3章两自由度系统

机械动力学第3章两自由度系统

b.微分方程
m1&&1 + (k1 + kc ) x1 − kc x2 = F1 (t ) x （3.1-1） ） m2 &&2 + (k 2 + kc ) x2 − kc x1 = F2 (t ) x
5
写成矩阵形式： 写成矩阵形式：
m1 0
0 &&1 k1 + kc x && + −k m2 x2 c
（3.1-12） ）
讨论（ 讨论（3.1-11）的解，假定 ）的解，
f (t ) = Be
st
代入（ 代入（3.1-11）得 ）
10
3.1无阻尼自由振动 3.1无阻尼自由振动
3.1.1 固有模态振动
QQ1094860954
s +λ =0
2
（3.1-13） ）
− −λt
（3.1-11）的通解 ）
f (t ) = B1e
（3.1-22） ）
17
3.1无阻尼自由振动 3.1无阻尼自由振动
3.1.1 固有模态振动
叫做特征向量, 叫做特征向量 振型向量或模态向量 r 1 r 2 叫做振型比 固有频率和振型向量构成系统的固有模态的基 或简称模态参数),它们表明了系统自由振动 本参数(或简称模态参数 本参数 或简称模态参数 它们表明了系统自由振动 的特性。 的特性。 两自由度系数有两个固有模态,即 两自由度系数有两个固有模态 即系统的固有 模态等于系统的自由度数。 模态等于系统的自由度数。 对于给定的系统, 对于给定的系统 特征向量或振型向量的相对比值 是确定的唯一的,和固有频率一样取决于系统的物 是确定的唯一的 和固有频率一样取决于系统的物 理参数,是系统固有的 而振幅则不同。 是系统固有的,而振幅则不同 理参数 是系统固有的 而振幅则不同。

第11讲两自由度振动

第11讲两自由度振动

对实际的工程系统，由于阻尼的存在，自由振动解会很快 地衰减掉，因此往往只关心受迫振动，受迫振动可写成：
x1 (t ) B1 sin t x2 (t ) B2
(2)
思考：为何与外部激励没有相位差？
因为忽略阻尼
x1 (t ) B 2 1 sin t x2 (t ) B2
对质量块m1： 对质量块m2：
m1 x1 k2 x2 x1 k1x1
m2 x2 k2 x2 x1
m1 x1 k1 k2 x1 k2 x2 0 m2 x2 k2 x1 k2 x2 0 (1)
x K x 0 M
称为系统的主振型，也可叫系统的固有振型。
当系统以某一阶固有频率振动时，称为系统的主振动。
第一阶主振动：
x1(1) A1(1) sin n1t 1
(1) (1) x2 A2 sin n1t 1 1 A1(1) sin n1t 1
(9)
第二阶主振动：
2 x 10 x 20 2 x10 x20 n1 2 1
2 2
A1(1)
四、自由振动特性
1、运动规律 1）两个简谐运动的合成； 2）各阶主振动所占的比例由初始条件确定（即振幅的 大小），但由于低阶主振动更容易被激起，因此一般情 况下总是低阶主振动占优势。 2、频率和振型 3、结点和结面
x1(2) A1(2) sin n 2t 2
(2) x2 2 A1(2) sin n 2t 2
(10)
讨论： 1）由于 1 0 ，因此如果系统作第一主振动时，根据 （9）可知，各点的运动方向相同。

工程力学中的自由振动和强迫振动的特性

工程力学中的自由振动和强迫振动的特性

工程力学中的自由振动和强迫振动的特性在工程力学中，振动是一个重要的研究领域。

振动被广泛应用于各种工程中，包括建筑结构、机械系统以及电子设备等。

振动可以分为自由振动和强迫振动两种类型。

本文将讨论自由振动和强迫振动的特性以及它们在工程中的应用。

一、自由振动的特性自由振动是指在没有外界干扰的情况下，结构或系统在其固有频率下进行的振动。

自由振动的特性主要包括振幅、周期、频率和阻尼等。

1. 振幅振幅是指振动的最大偏离量。

在自由振动中，振幅受到初始条件的影响，振幅越大，振动的能量也就越大。

2. 周期周期是指振动完成一个完整循环所需的时间。

自由振动的周期与结构的固有频率有关，固有频率越高，周期越短。

3. 频率频率是指振动单位时间内完成的循环次数。

频率是周期的倒数，用赫兹（Hz）表示。

自由振动的频率与周期相反，固有频率越高，频率越大。

4. 阻尼阻尼是指振动过程中能量的消耗。

在自由振动中，存在三种类型的阻尼：无阻尼、过阻尼和欠阻尼。

无阻尼振动指没有能量损耗的理想振动；过阻尼振动是指能量损耗过大，振动停止得很慢；欠阻尼振动是指振动的能量损耗较小，但是在振动停止时存在振荡。

二、强迫振动的特性强迫振动是指受到外界周期性力作用下的振动。

外界力的频率通常不等于结构的固有频率，因此会引发结构的共振。

强迫振动的特性主要包括固有频率、共振和受迫振动等。

1. 固有频率固有频率指的是结构或系统在自由振动状态下的固有频率。

在强迫振动中，结构的固有频率决定了其对外界激励的响应。

2. 共振共振是指外界力的频率与结构的固有频率相等或接近，导致结构振幅迅速增大的现象。

共振现象对于某些结构来说是有害的，因为会导致结构破坏或崩溃。

3. 受迫振动受迫振动是指在强迫振动中，结构受到外界激励而发生的振动。

外界激励可以是周期性的力或者者是其他形式的周期性变量。

三、自由振动和强迫振动在工程中的应用自由振动和强迫振动在工程中有着广泛的应用。

1. 自由振动的应用自由振动的研究可以用于建立结构的固有频率，通过调节结构的初始条件和强度来影响振动的特性。

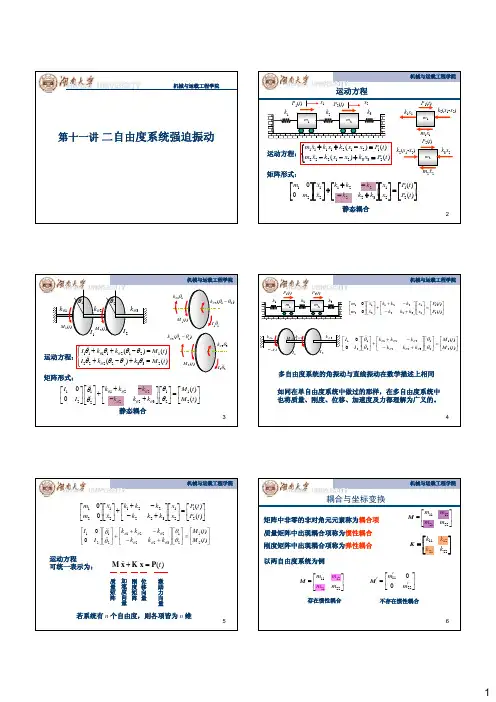
第十一讲—二自由度系统强迫振动

第十一讲—二自由度系统强迫振动

机械与运载工程学院第十一讲二自由度系统强迫振动2机械与运载工程学院运动方程m 1m 2k 3k 1k 2x 1x 2P 1(t )P 2(t )k 1x 1k 2(x 1-x 2)11x m m 1P 2(t )k 2(x 1-x 2)22xm m 2k 3x 2⎩⎨⎧=+−−=−++)()()()(2332122212121111t P x k x x k x m t P x x k x k x m 运动方程：矩阵形式：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+−−++⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡)()(0021213222212121t P t P x x k k k k k k x x m m3机械与运载工程学院1θk 1I 2θ2I 2θk 3θk )(1t M )(2t M 1θ11θθk 11θ I )(1t M )(212θθθ−k 22θ I )(2t M 33θθk )(122θθθ−k 1111121212222332()()()()I k k M t I k k M t θθθθθθθθθθθ⎧++−=⎪⎨+−+=⎪⎩运动方程：矩阵形式：122111122322220()0()k k k I M t k k k I M t θθθθθθθθθθ+−⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤+=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥−+⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦ 4机械与运载工程学院⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+−−++⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡)()(0021213222212121t P t Px x k k k k k k x x m m⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+−−++⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡)()(0021213222212121t M t M k k k k k k I I θθθθθθθθθθ 多自由度系统的角振动与直线振动在数学描述上相同如同在单自由度系统中做过的那样，在多自由度系统中也将质量、刚度、位移、加速度及力都理解为广义的。

第三章 两自由度系统的振动

第三章 两自由度系统的振动

设两质量块振动时按同频率和同相位作简谐振动，即：令
一组解x1 A1 sin( t )、x2 A2 sin( t )，代入方程后得： [(a 2 ) A1 bA2 ]sin( t ) 0 [cA1 (d 2 )A2 ]sin( t ) 0
(a 2 ) A1 bA2 0
cA1
(d
一阶主振型。
例
练习1 如图，推导系统的频率方程并 求主振型。设滑轮为均质圆盘， 其质量为m2，质量块质量为m1， 弹簧刚度分别为K1和K2，并假定 滑轮与绳索间无相对滑动。
解：选取广义坐标为（ ），
取静x,平 衡位置作为坐标原点，
进行受力分析，建立系统的运 动微分方程：
m1x K1(x r) I0 K1(x r)r K2r 2
1) 当作用于系统的主动力都是有势力时（系统没有能
量损失时），则系统具有势能U（q1,q2,···,qn)，广义力
为
Qj
U q j
( j 1, 2, , n)
代入方程得： d ( T ) T U 0 dt qj q j q j
( j 1, 2, , n)
或
d ( L ) L 0 ( j 1, 2, , n)
m1l 21 (m1gl Ka2 )1 Ka22 0 m2l 22 Ka21 (m2gl Ka2 )2 0
1 2
K2 (u2 u1)2
u1
u2
代入拉氏方程，得系统的微分方程
(m1
m2 2
)u1
m2 2
u2
(K1
K2 )u1
K2u2
0
m2 2
u1
3u2 2
u2
K 2u1
K2u2
0
m1

二自由度振动有阻尼及强迫振动响应

二自由度振动有阻尼及强迫振动响应
12224133442413111333031133sin333wwwwwwwwwwwwwwt?????????????????????????式39这样我们就将式31变成式39由于式39只有4个一阶微分方程所以代入到ode45函数并给出求解初值和区间便可以解出两个质量块在物理坐标系下的解
Harbin Institute of Technology
7
哈尔滨工业大学课程设计
理坐标系下： x(1)= 1.27*10^(-4)*cos(1.99*t)*(62.3*cos(1.01*t) - 2.65*cos(4.99*t) + 315.0*sin(1.01*t) - 66.1*sin(4.99*t)) - 0.0236*sin(3.0*t) - 0.00203*cos(3.0*t) + (0.502*cos(1.41*t))/exp(0.1*t) + (0.0859*sin(1.41*t))/exp(0.1*t) + (0.492*cos(1.99*t))/exp(0.2*t) + (0.00198*sin(1.99*t))/exp(0.2*t) + (0.236*sin(1.99*t)*(0.169*exp(0.2*t)*cos(1.01*t) + 0.0355*exp(0.2*t)*cos(4.99*t) - 0.0335*exp(0.2*t)*sin(1.01*t) 0.00142*exp(0.2*t)*sin(4.99*t)))/exp(0.2*t) x(2)= (1.51*cos(1.41*t))/exp(0.1*t) - 0.0709*sin(3.0*t) 3.8*10^(-4)*cos(1.99*t)*(62.3*cos(1.01*t) - 2.65*cos(4.99*t) + 315.0*sin(1.01*t) - 66.1*sin(4.99*t)) - 0.00608*cos(3.0*t) + (0.258*sin(1.41*t))/exp(0.1*t) - (1.48*cos(1.99*t))/exp(0.2*t) (0.00593*sin(1.99*t))/exp(0.2*t) (0.707*sin(1.99*t)*(0.169*exp(0.2*t)*cos(1.01*t) + 0.0355*exp(0.2*t)*cos(4.99*t) - 0.0335*exp(0.2*t)*sin(1.01*t) 0.00142*exp(0.2*t)*sin(4.99*t)))/exp(0.2*t) 利用 Matlab 作图可得图（3-2） ，图中实线为图（2-1）中的质量块 1 的运动，图中 虚线为图（2-1）中的质量块 2 的运动。

有阻尼强迫振动微分方程及其解

有阻尼强迫振动微分方程及其解
qn2q 0
解为：
q Asin(nt )
8
设 t = 0 时，q q0 , q q0 则可求得：
A
q02
q02
2 n
,
arctg
n q0
q0
或：
q C1cosn t C2 sinn t
C1，C2由初始条件决定为 C1 q0 , C2 q0 /n
q
q0
cos nt
q0
n
sin
nt
9
三、自由振动的特点：
令
n2
k m
,
n
c 2m
则 x2nxn2 x0
有阻尼自由振动微分方程的标准形式。
24
其通解分三种情况讨论：
1、小阻尼情形 (n n) c 2 mk
x Ae nt sin(d t )
d n2 n2 —有阻尼自由振动的圆频率
设 t 0 时, x x0 , x x0 , 则
A
x02
(
x0 nx0 )
的固有频率、激振力的频率及激振力的力幅有关。 31
(1) =0时
b0
h
2 n
H k
(2) n 时，振幅b随 增大而增大；当 n 时，b
(3) n 时，振动相位与激振力相位反相，相差 rad 。
b h
n2 2
b 随 增大而减小； 2n时 , bb0; 时b0
— 振幅比或称动力系数
20
Tm
ax
1 2
M
(
xm
ax)
2
1 2
M
2
(
x m a x R
)
2
1 2
m(
R R
r
xm

简谐激励下强迫振动的响应特性

简谐激励下强迫振动的响应特性

1 s 2 t 0 in 0
c1
100.05(m) 200
c2 0
例（1）
The solution: x t A c2 o t B 0 s s2 it n 0 . 0 0 tc 5 2 o t 0 s
A and B are determined using the initial conditions
mg
Substitute above equations in equation of motion to obtain
2 c 1 s 0 2 t i c 2 0 c n 0 2 t o 2 0 t c 1 s c 0 2 t o c 0 2 s 0 2 t s i 0 2 n 0 t c 1 c 0 2 t o c 0 2 s 0 2 t s i 0
x00 A0 x t 2 0 B c o s 2 0 t 0 . 0 5 c o s 2 0 t t s i n 2 0 t x00 B0.050.0025(m )
20
Hence, the complete response of the undamped system is
x t 0 .0 0 2 5 s i n 2 0 t 0 .0 5 tc o s 2 0 tm
1
12 2 22
X0 k
F0
12 222
稳态响应的高频特性
, 0 , , X 0 F k 0 n 2 2 m F 0 2
(Inertia domination)
（外力主要与惯性力平衡）
Φarctan122
1
12 2 22
X0 k
F0
12 222
稳态响应的共振特性
x 2 t tc 1 c2 o t c 0 s 2 s2 itn 0

第11讲 二自由度系统受迫振动及吸振

第11讲 二自由度系统受迫振动及吸振

2
多自由度系统强迫振动 \ 吸振
多自由度系统强迫振动 \ 吸振 故系统受迫振动响应为
例1 线。
图a所示的系统中，已知m1 m, m2 2m，k1 k2 k, k3 2k, Q2 0.
(1)试求系统的响应；（ 2）计算共振时的振幅比；（3）做振幅频率响应曲
解：（1）由已知
K11 2k , K12 K 21 k , K 22 3k
则微分方程式可写成
M 11 x1 K11 x1 K12 x2 Q1 sin t M 22 x2 K 21 x1 K 22 x2 Q2 sin t
（2）
多自由度系统强迫振动 \ 吸振
多自由度系统强迫振动 \ 吸振
M 11 x1 K11 x1 K12 x2 Q1 sin t （2） M 22 x2 K 21 x1 K 22 x2 Q2 sin t



k
k 2 F1
1
2 k 2 m1 2 k 2 m 2 2 k 2



22 m2 F 1 k11 m1 2 k22 m2 2
k


2 2 m2 F 1 2 k1 k2 m1 k2 m2 2
k




m1m2 4 m1k 2 m2 k1 k 2 2 k1k 2
• 方程（2）是二阶线性常系数非齐次微分方程组，它 的解应由齐次方程组的通解（自由振动）与非齐次方 程组的特解（受迫振动）叠加而成。其中非齐次方程 的特解为稳定阶段的等幅振动，系统按与激振力相同 的频率 ，作受迫振动。
对（3）式求二次导数，即得加速度
x1 B1 2 sin t

4二自由度系统振动

4二自由度系统振动

)
)
0
0
sin( t ) 0
( a 2 )A1 bA2 0
cA1
(
d
2
)A2
0
这是关于 A1 和 A2 的线性齐次代数方程组。显然，A1 A2 0 是它的解， 对应于系统处于静平衡的情况。若要使 A1 与 A2 具有非零解，此方程组
的系数行列式必须等于零，即：
2
F1(t ) F2 (t )
2.1 两自由度系统的振动微分方程
写为矩阵形式：
m1
0
0 m2
x1 x2
c1 c2
c2
其中定义：
c2 c2 c3
x1 x2
k1 k2
k2
k2 k2 k3
x1 x2
F1 F2
(t (t
) )
M
m1
0
0
m2
,
C
c1 c2
但是必须指出并非任何情况下系统都可能作主振动。
x1 ax1 bx2 0 x2 cx1 dx2 0
此方程组的通解是振系的两个主振动的叠加
x1 x2
x1(1) x2(1)
x1(2) x2(2)
x1 r (1) A2(1) sin(1t 1) r (2) A2(2) sin(2t 2 )
x1 x2
F1 F2
(t (t
) )
扭转振动系统
两者坐标形式相同
2.1 两自由度系统的振动微分方程
运动微分方程的矩阵形式
定义：x x1 x2 T x x1 x2 T
x x1 x2 T
F(t) F1(t) F2 (t)T
位移向量； 速度向量； 加速度向量； 激励向量；
矩阵形式的运动微分方程Mx Cx Kx F(t)

03二自由度系统的振动

03二自由度系统的振动

[u]T [M ][u]{&y&} + [u]T [K ][u]{y} = {0}
y 0 &&1 k1 + m 2 &&2 0 y 0 y1 0 = k 2 y 2 0
结果有 即是
m1 &&1 + k1 y1 = 0 y m 2 &&2 + k 2 y2 = 0 y
将方程组用矩阵表示如下: 将方程组用矩阵表示如下
m1 0
0 &&1 k1 + k 2 x + m 2 &&2 − k 2 x
− k 2 x1 0 = k 2 + k 3 x 2 0
一般可表示为: 一般可表示为
[M ]{&&} + [K ]{x} = {0} x
11/41
一般可表示为: 一ห้องสมุดไป่ตู้可表示为
m11 m 21
或:
m12 &&1 k11 x + m 22 &&2 k 21 x
k12 x1 0 = k 22 x 2 0
[u] =
u11 u21
u12 u22
而坐标变换为
12/41
{x} = [u]{y}
{&&} = [u]{&&} x y
一般化分析与推导如下： 一般化分析与推导如下：
m11 m 21
设变换矩阵为
m12 &&1 k11 x + m 22 &&2 k 21 x

第三章 两自由度系统振动

第三章 两自由度系统振动
解：m取 1、m2偏离平衡位置x1的 及x位 2为移 广义坐标。阻尼 拉系 氏统 方的 程可表示为
d d( tq L j) q L jQ j - q D j (j 1 ,2 , ,n )
式D 中 1 2 C 1 x 1 2 1 2 C 2 (x 1-x 2)2 1 2 C 3 x 2 2
例题： 置于光滑平面的小车质量m1，车上质量为m2的圆柱体可作 无滑动的纯滚动。试建立该系统的运动微分方程。
两自由度与单自由度系统振动特性与分析方法的不同：
①两自由度振动系统具有两阶固有频率； ②两自由度振动系统引入主振型的概念，与系统的固
有频率一样，是系统本身的物理特性与固有特性， 与其初始条件无关。 ③一般情况下系统的振动是两种主振动的叠加，是一 种复杂的非周期运动。当满足一定条件时，系统才 作主振动。
(j1,2, ,n)
或
dd(tqLj)qLj 0 (j1,2, ,n)
(1)
其中，L=T-U称为拉格朗日函数。
2)当作用在系统上的主动力中，部分为有势力，部分 是非有势力，广义力Qj可分为两部分：
Qj Qj Q (j1,2,,n) 其中 Q是对应于非有 义势 力力 Q， j是 的对 广应于有势 广义力。 拉氏方程可写成
1
第三节 两自由度系统振动模型的建立
动力学系统振动模型的建立方法： 牛顿运动定律 定轴转动微分方程 能量法
一、拉氏方程的原理
在理想、完整约束条件下的n个自由度系统，选取广义坐 标为qj（j=1,2, ···,n)，其运动可由如下拉格朗日方程来描述：
dT T d( tq j)qj Q j
取静x,平衡位置作为坐标原点，
进行受力分析，建立系统的运 动微分方程：
m1x K1(x r) I0 K1(xr)r K2r2

二自由度系统的振动

二自由度系统的振动

6.3.1 频域分析
首先分析受谐波激励的情况： 系统运动微分方程组是 Mu(t) Ku(t) F sin t
F
f1
f
2
方程特解为：
u(t) U sin t
代入到方程中得到： (K 2M )U F
U
u1
u2
定义：
def
Z() K 2M
为系统的动刚度矩阵。
其元素zij反映了系统第j个自由度具有单位位移响应 sinωt，而其余坐标不动时，应施加在第i个自由度 上的正弦广义力的幅值。
12
0 0
线性方程组
k11 m12
k12
k21
k22
m22
特征矩阵
r r2
特征值（特征根）
12rr
（r
=1,2）
与特征值对应的特征向量
6.2 无阻尼多自由度系统自由振动
将固有频率ω代入系统线性方程，得到系统作第一、二阶
固有振动时两质量块振幅之比，分别为：
s1
def
11 21
k11
由于在N自由度无阻尼系统总有N个线性无关的固有 振型φr，因此可以把它作为基底来张成系统运动空 间。
6.2 无阻尼多自由度系统自由振动
引入坐标变换： u q
代入到：Mu(t) Ku(t) 0
其中：u为物理坐标，q为模态坐标，Φ为固有振型矩阵。
得到：
Mq(t) Kq(t) 0
两边左乘 T
T Mq(t) T Kq(t) 0
二自由度微分方程组特点：
k2 u1
k2
k3
u2
f1 f2
1、形式上与单自由度系统受迫振动微分方程相同。但M，K，C 不是常数，而是矩阵。

3两自由度系统振动2

3两自由度系统振动2
2
解方程，进一步可得如下的两个根：
ac ac c a b n 21,2 2 2
ac ac bc 2 2
2
n2
上式是决定系统频率的方程，并称为振动系统的特征 方程。
结论：两个自由度振动系统具有两个固有频率 ，这两个固有频率只与振动系统的质量和刚度 等参数有关，而与振动的初始条件无关。 n1 n2 将所求得的 和 代入（3.7）式中可得： 2 1 a n A 2 c 1 1 1 c n 21 b A1
上式就是机械振动系统在上述初始条件下的响应。
1x 10x 20 2 1 (2x10x20) ( 2 A(1) 1 2 1 n1 )
利用主坐标解耦的方法求解系统响应
的基本步骤为： （1）求出原振动方程的固有频率和振幅 比，得到振型矩阵；
（2）求出主坐标下的响应；
（3）利用反变换式得出原广义坐标下的 响应； （4）利用初始条件确定常系数。
上式为两自由度系统振动的微分方程。
图3.2，双质量－弹簧机械振动系统中，第一个方程中 包含 bx 2 项，第二个方程中则包含 cx 1 项，统称为 “耦合项”。
以上表明，质量 m1同不仅受到弹簧 k1的恢复力的作用，而 且受到弹簧k2 的恢复力的作用； m2只受一个弹簧 k2恢复力 的作用，还受到第一质点m1 位移的影响。位移之间有耦合 称为弹性耦合；加速度之间有耦合称为惯性耦合。
,
2

2
故机械振动系统的响应为：
x1 0.4cos x 0.4cos 2
（1）运动规律
k t 0.8cos1.581 m k t 0.4cos1.581 m
k t m k t m

常微分四类振动方程

常微分四类振动方程
d 2 dt 2 g 0 l
特征方程：
g 0 l
2
i,
g l
通解： (t ) c1 cost c 2 sint , c1 , c1为任意常数.
（4.41） A，θ为任意常数
(t ) A sin( t )
周期T与初始 状态无关，只 与摆长l相关
d 2
比较系数法： 非齐次特解：
随时间增大 振幅将无限大ห้องสมุดไป่ตู้从而破坏系统结构
非齐次通解： 自由周期振动
+
外力强迫振动
=非周期振动
共振现象：当外力频率p（达到）无限接近于系统 固有频率ω（即使外力振幅H很小），系统振幅将 （无限）充分大，从而破坏系统自身结构的现象！
4. 阻尼强迫振动

g , 2n l m
~ t k [ M cos t N sin t ]e t , 非齐次特解： 0, p, k为 i重数
分两种情况：
~ M cos pt N sin pt, (i ) p ( pi非特征根)： ~ t ( M cos pt N sin pt (ii) p ( pi特征根)：
特解
d 2 dt 2
2n
d 2 H s in p t dt
特解
振幅什么条件下最大？
利用外力 （圆）频率 可实现振幅 最大化！
非齐次通解：
自由阻尼衰减振动 （时间充分大可忽略）
+
外力强迫周期振动 =非周期振动 （主项）
振动主项中，但如果外力园频率p达到（或接近于）某固定频率， 即使施加的外力不大，随时间增长，质点振动运动的振幅将达到 最大。 共振现象 该频率称共振频率

机械振动知识总结

机械振动知识总结

一、单自由度系统的振动2()()0()(nmx t kx t x t w x t +=⇔+120)cos sin cos n n A w t A w t x =+=2()()()0()2()()0n n mx t cx t kx t x t w x t w x t ξ++=++= 211)(nn w t w t e X e ξξ--=+自然频率 阻尼率 22n c c mw mkξ==w 2()2()(()cos(n n nw td x t w x t w x t t C ew t ξξψ-++=-：尼激0 ()cos(n x t C w t =-幅频曲线及其特性 ()H w 1：此时力与位移相位相反sin nwt c =/2/22T T T -=⎰周期函数将失去周期性，而离散频谱将转化为连续谱，此时傅里()()(mx t cx t kx t ++21)[1(/)n n c k w w ∞==-∑00sin n dx x ξωω+0sin n n x t ωω +自由振动是强迫振动的基础，任一时刻的强迫振动响应其实只是该时刻前被激起的一系列自由振动的叠加。

2()2()()n nx t w x t w x t ξ++=1()()()2iwtt H w F w e dw π+∞-∞=⎰()()()mx t cx t kx t ++=拉普拉斯变换：()(0)(()()()F s mx ms X s D s D s ++=+拉氏反变换：11()[()]2jw jwx t L X s j γγπ+--==⎰牛顿第二定律、定轴转动方程、能量原理、拉格朗日方程一般情况采用解析法求解，对于非线性方程，常采用数值方法求解振动系统反作用力近似为位移和速度的函数：)x 泰勒展开并取cx 结论：弹簧刚度与阻尼系数实际上是泰勒展开式中定义：单位位移所需要的力。

弹簧串联、并联，关键在于共力还是共位移用积分计算结构运动时的动能，得到某结构的等效质量/d m ；经变形法；能量法：max V不变，响应振幅与激振力振幅正比，为滞后激励多少，Ψ初相位微小的阻尼就可以限制振幅的无限扩大共振需要一个较长的建立过程，机器需有足够的加速功率顺利通过共振区。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

理论上已经证明， 只要函数 f(t,y(t)) , y(tn ) 。
适当光滑，可以确认式（2-7）初值问题的解存在并且唯一的。 在本题中将采用 MATLAB 的 ode45 （） 函数对已经解耦的方程进行数值积分求解。 ode45 （）函数使用的是显式 Runge-Kutta(4,5)法则与 Dormand prince 组合解法的中阶解法， 所以特别适用于仿真线性化程度高的系统。由于 ode45（）函数计算快，一般来说，在解 题的第一次仿真时，采用 ode45（）函数是最佳选择。
2
哈尔滨工业大学课程设计
一 引言
机械动力学是机械原理的主要组成部分。它研究机械在运转过程中的受力、机械中 各构件的质量与机械运动之间的相互关系，是现代机械设计的理论基础。研究机械运转 过程中能量的平衡和分配关系。主要研究的是：在已知外力作用下，求具有确定惯性参 量的机械系统的真实运动规律、分析机械运动过程中各构件之间的相互作用力、研究回 转构件和机构平衡的理论和方法、机械振动的分析、以及机构的分析和综合等等。 由于本次作业主要研究的是“二自由度振动有阻尼及强迫振动响应”问题，所以本 文将先对该问题的两种解法进行相关的介绍，这两种方法分别是：解耦法和数值法。然 后根据课上给出的具体实例，应用这两种方法给出最终的结果。通过比较这两种结果， 加深我们对“二自由度振动有阻尼及强迫振动响应”问题的理解，并且在解决问题的过 程中，提高我们运用 MATLAB 的能力。
三 实例
3.1 问题描述
6
哈尔滨工业大学课程设计
3.2 解耦法求解
系统的图示为图（2程的矩阵表示：
9 0 2.7 0.3 27 3 0 0 1 x 0.3 0.3 x 3 3 x 1 sin 3t
式（3-3）
由式（3-3）可以看到，通过解耦法我们将原本耦合的二自由度有阻尼受迫振动系统 分解成了两个互不耦合的单自由度系统。利用坐标变换求出模态坐标下的初始条件后利 用 Matlab 里的 dsolve（）函数对微分方程进行求解，并用 simplify（）函数对求出的 解进行化简，我们可以得到模态坐标下的振动响应： r(1)= 0.0086*cos(3.0*t) + 0.1*sin(3.0*t) - (2.13*cos(1.41*t))/exp(0.1*t) (0.364*sin(1.41*t))/exp(0.1*t) r(2)= - 5.38*10^(-4)*cos(1.99*t)*(62.3*cos(1.01*t) - 2.65*cos(4.99*t) + 315.0*sin(1.01*t) - 66.1*sin(4.99*t)) - (2.09*cos(1.99*t))/exp(0.2*t) (0.00839*sin(1.99*t))/exp(0.2*t) - (sin(1.99*t)*(0.169*exp(0.2*t)*cos(1.01*t) + 0.0355*exp(0.2*t)*cos(4.99*t) - 0.0335*exp(0.2*t)*sin(1.01*t) 0.00142*exp(0.2*t)*sin(4.99*t)))/exp(0.2*t) 在得到模态坐标下的振动响应后，通过坐标变换将模态坐标下的振动响应变换到物
4．
化为：
P M 2 CM 2 P M 2 KM 2 P M

1

1

1

1

1 2
1 0 F1 0 1 F 2
式（2-5）
在方程式（2-5）两端同时左乘 PT ，方程化为：
PT M 2 CM 2 P PT M 2 KM 2 P PT M
式（2-1）
式（2-2）
将式（2-1）和式（2-2）写成矩阵形式，可以得到其振动的微分方程，用式（2-2） 表示。
1 0 F1 Mx Cx Kx BF (t ) 0 1 F2
式（2-3）
式中 M 为质量矩阵，C 为阻尼矩阵，K 为弹簧刚度矩阵。 解耦法的实质就是将微分方程式（2-3）的左侧矩阵都化成对角阵，这样就将两个耦 合的微分方程式（2-1）和式（2-2）化成两个互相不耦合的微分方程，大大简化了问题 的求解难度。在得出解耦的解后，还要利用坐标变换将解耦的解转换到物理坐标系下。 具体求解可分为八个步骤：
二 解法介绍
2.1 解耦法
图 2-1 二自由度振动有阻尼及强迫振动响应系统 如图 2-1 所示是一个典型的二自由度振动有阻尼及强迫振动响应系统， 其中 k1 、k 2 是 弹簧刚度系数， c1 、 c2 是阻尼系数， F1 、 F2 是两个质量块所受的外力， x1 、 x2 是两个质 量块的位移。 m1 、 m2 两个质量块在外力作用下做受迫振动，分别对两个质量块进行受力 分析，如图 2-2 所示。
2 做变量替换，令 x M q ，并在方程两侧同左乘 M 2 将微分方程的第一项系

1
1
1．
数 M 消掉。此时方程变为：
q M CM q M KM q M

1 2

1 2

1 2

1 2

1 2
1 0 F1 0 1 F 2
式（2-4）
4
哈尔滨工业大学课程设计
式（3-1）
在 Matlab 中使用函数 chol（）对质量矩阵 M 进行乔里斯基分解，从而求出 M 用关系式 x M q 对 x 进行变量替换，并且在方程两端同乘以 M 为：
1 2
1 2

1 2
。利
，则式（3-1）可以化
0.3 0.1 3 1 0 q q q sin 3t 0.1 0.3 1 3 1
2.2 数值积分法
dy (t ) f (t , y (t )) a t b y dt y (a) y0
式（2-7）
所谓数值积分解法就是通过数值积分的算法逐个求出区间[a,b]内若干个离散点
a t0 t1 tn b 处的近似值 y(t1 ), y(t2 ),
式（3-2）
为了继续对角化系数矩阵，我们可以先求出 q 的系数矩阵的特征向量 P，令 q Pr 做
变量替换。 然后方程两端同时左乘该特征向量的转置， 并同时右乘该特征向量， 则式 （3-2）
可以化为：
0
0.2
0 2 0 0.7071 sin 3t 0.4 0 4 0.7071
5． 6．
计算 S M P 和 S 的逆矩阵。 计算模态坐标下的初始条件 r (0) S 1 X 0 ， r (0) S 1 X 0 。

1 2
7．
在模态坐标下求解解耦后的振动响应 r (t ) 。
5
哈尔滨工业大学课程设计
8．
求解物理坐标下的振动相应 x(t ) Sr (t ) 。
7
哈尔滨工业大学课程设计
理坐标系下： x(1)= 1.27*10^(-4)*cos(1.99*t)*(62.3*cos(1.01*t) - 2.65*cos(4.99*t) + 315.0*sin(1.01*t) - 66.1*sin(4.99*t)) - 0.0236*sin(3.0*t) - 0.00203*cos(3.0*t) + (0.502*cos(1.41*t))/exp(0.1*t) + (0.0859*sin(1.41*t))/exp(0.1*t) + (0.492*cos(1.99*t))/exp(0.2*t) + (0.00198*sin(1.99*t))/exp(0.2*t) + (0.236*sin(1.99*t)*(0.169*exp(0.2*t)*cos(1.01*t) + 0.0355*exp(0.2*t)*cos(4.99*t) - 0.0335*exp(0.2*t)*sin(1.01*t) 0.00142*exp(0.2*t)*sin(4.99*t)))/exp(0.2*t) x(2)= (1.51*cos(1.41*t))/exp(0.1*t) - 0.0709*sin(3.0*t) 3.8*10^(-4)*cos(1.99*t)*(62.3*cos(1.01*t) - 2.65*cos(4.99*t) + 315.0*sin(1.01*t) - 66.1*sin(4.99*t)) - 0.00608*cos(3.0*t) + (0.258*sin(1.41*t))/exp(0.1*t) - (1.48*cos(1.99*t))/exp(0.2*t) (0.00593*sin(1.99*t))/exp(0.2*t) (0.707*sin(1.99*t)*(0.169*exp(0.2*t)*cos(1.01*t) + 0.0355*exp(0.2*t)*cos(4.99*t) - 0.0335*exp(0.2*t)*sin(1.01*t) 0.00142*exp(0.2*t)*sin(4.99*t)))/exp(0.2*t) 利用 Matlab 作图可得图（3-2） ，图中实线为图（2-1）中的质量块 1 的运动，图中 虚线为图（2-1）中的质量块 2 的运动。
3
哈尔滨工业大学课程设计
图 2-2 两个质量块受力分析 通过对两个质量块的受力分析，我们可以分别写出两个质量块振动的微分方程：
m1 x1 c1 x1 c2 ( x2 x1 ) k1 x1 k2 ( x2 x1 ) m2 x2 c2 ( x2 x1 ) k2 ( x2 x1 )
从式（2-4）可以看出微分方程的第一项系数已经被消掉。
2．
令 Kw M 2 KM

1

1 2
、 Cw M 2 CM

1