初中数学弧长及扇形的面积课件

格式：ppt
大小：634.50 KB
文档页数：17

下载文档原格式

初中数学《弧长及扇形的面积》公开课课件

（1）要求扇子外围的弧长，需要知道哪些量？
（2）怎样求这把扇子一面用纸的面积？
圆心角度数，半径长度
大扇形面积—小扇形面积
弧长和扇形的面积公式
如果扇形的半径为r，圆心角为n°，那么

=

扇形 =

1
扇形 =
2
探求新知3——求弓形的面积
A
S阴影= S扇形-S△
B
S阴影=
2.观察该公式，它与我们学过的哪一个公式很类似？
弧长和扇形的面积公式
如果扇形的半径为r，圆心角为n°，那么

=

扇形 =

1
扇形 =
2
练习2
1. 已知扇形的圆心角为120°，半径为20，则该扇形的面积____.

2.已知扇形面积为
3
，圆心角为60°，则这个扇形的半径R=___.
探索新知1——弧长公式
例1：制造弯形管道时，要先按中心线计算“展直长度”，再下料，
试计算图中所示管道的展直长度 l (结果保留，单位：mm)
思考：
展直长度指的是谁的长？
探求新知1——弧长公式
练习1
1.一个扇形半径是3，圆心角是240°，这个扇形的弧长是( C )
A. 2π
B. π
C. 4π
D. 12π
：
（2）说一说你是如何计算每一个弧长的。
圆心角的度数n°
360°
180°90°ຫໍສະໝຸດ 60°1°n°
计算过程
扇形的弧长 l
探索新知1——弧长公式
活动（1）已知扇形半径为r，请计算不同圆心角度数所对的弧长，并填表。
：
（2）说一说你是如何计算每一个弧长的。

弧长年级扇形的面积课件共ppt

弧长级扇形的面积课件共份ppt（PPT 优秀课件）
知识点 2 扇形面积公式
知2－导
同学们已经学习了扇形：由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形．你能否类比刚才我们研究弧长公式的方法推导出扇形面积的计算公式？
弧长级扇形的面积课件共份ppt（PPT 优秀课件）
弧长级扇形的面积课件共份ppt（PPT 优秀课件）
S扇形
1 2
lR
其中l为扇形的弧长，R为半径.
弧长级扇形的面积课件共份ppt（PPT 优秀课件）
弧长级扇形的面积课件共份ppt（PPT 优秀课件）
例2 如图1，水平放置的圆柱形排水管道的截
面半径是0.6 m，其中水面高 0.3 m，
求截面上有水部分的面积（结果保留小
数点后两位）．
解：如图2，连接OA，OB，作弦AB的垂直平分线，垂足为D，交A⌒B于点C，连接AC.
（3）1°圆心角所对的弧长是多少？
（4）n°圆心角所对的弧长是1°圆心角所对的弧长的多少倍？（5）n°圆心角所对的弧长是多少？（1）C=2πR
（2）360°
（3）2πR πR 360 180
n°
（4）n 倍
o
（5）l nπR 180
也可以用A⌒Bl表示A⌒B的长.
知1－讲
例1 制造弯形管道时，经常要先按中心线计算“展直长度”，再下料，试计算如图所示的管道的展直长度L（结果取整数）.
n 1
8
R 0
,
并运用公式进行计算.
2.扇形的面积公式S＝
nR 2 360
,并运用公式进行计算.
3.弧长l及扇形的面积S之间的关系，S 扇形
=
1 2

初中数学《弧长及扇形的面积(1)》优课PPT课件

180
辨一辨：
下列各命题是真命题还是假命题.
× 1、度数相等的弧是等弧; × 2、长度相等的弧是等弧;
√ 3、在同圆或等圆中,度数相等的弧是等弧;
√ 4、在同圆或等圆中,长度相等的弧是等弧;
应用公式：
1.半径为1㎝的圆弧所对的圆心角的度数是60° 求这条弧长。
2.直径为100㎝的圆弧的度数是20°，
A′
C
A
B C′
l
.一块等边三角形的木板,边长为1,现将木板沿水平线翻滚(如图),那么B点从开始至 B2结束所走过的路径长度________.
(湖北) B1
B●
B
B2
B1
F'
U
A
BC
DE
FB2
1.弧长与哪些因素有关？
（1）与圆心角的大小有关
（2）与半径的长短有关
2. 弧长公式：
l nR
180
l弧＝
n 360
C圆
3. 弧长单位：
弧长带长度单位
如图，某田径场的周长为400m，其中两个半圆弯道的内圈共长200m，每条直道长100m，且每条跑道宽1m（共 6条跑道）（1）内圈弯道半径为多少m（精确到0.1m）？
（2）内圈弯道与外圈弯道的长相差多少米（精确到0.1m）？（3）相邻两圈的长度之间有什么规律？
求这条弧长（结果保留）。
3、已知圆的半径为 17 cm，圆心角为1500。求这个圆心角所对的2弧长。
公式变形
1.已知半径为5㎝的圆弧长5㎝，求这条弧所对圆心
角的度数
l n R
180
n 180l
R
2.已知弧长为40 ㎝，弧的半径为20㎝，

《弧长及扇形面积的计算》数学教学PPT课件(3篇)

弧长和扇形面积的计算
知识回顾
o rp
圆的周长公式 C=2πr
圆的面积公式 S=πr2
问题情景：
如图是圆弧形状的铁轨示意图，其中铁轨的半径为100米，圆心角为90°．你能求出这段铁轨的长度吗?
解:∵圆心角900
∴铁轨长度是圆周长的
图 23.3.1
则铁轨长是 1 2 100 50米
4
上面求的是的圆心角900所对的弧长，若圆心角为n0，如何计算它所对的弧长呢？
1个圆面积 1 个圆面积
4
1 个圆面积
2
3 个圆面积
4
圆心角是10的扇形面积是多少？
圆心角是10的扇形面积是圆面积的3160
圆心角为n0的扇形面积是多少?
圆心角是n0的扇形面积是圆面积的3n60
如果用字母 S 表示扇形的面积，n表示圆心角的度数，r 表示圆半径，那么扇形面积的计算公式是：
S扇形＝
1 2 rl
弧长与圆的周长有关，扇形的面积与圆的面
积有关。因此，计算弧长是形的面积时是 n S圆。
n
360 C圆
；而计算扇
360
小试牛刀：
1、如果扇形的圆心角是2３0°，那么这个扇形的
面积等于这个扇形所在圆的面积的_____；
2、扇形的面积是它所在圆的面积的
2 3
，这个扇
形的圆心角的度数是_______。
思考：
请同学们计算半径为 r，圆心角分别为1800、900、 450、n0所对的弧长。
图 23.3.2
圆心角占整个周角的
1800
180
360
所对弧长是
180 2r
360
900
90
90 2r

弧长和扇形的面积课件PPT(1)

∴ =
90π·4
=2π,
180
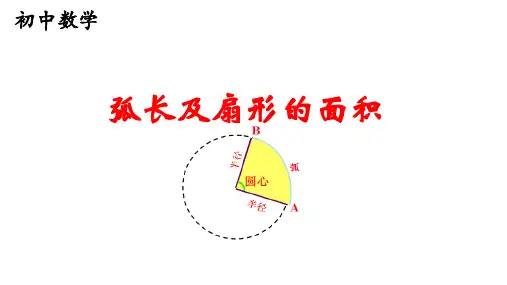
扇形 OAB
90π×42
的面积= 360 =4π,
∴2π·DC=2π,∴DC=1.在 Rt△SDC 中,SC=4,SD= 2 - 2 =
42 -12 = 15,
∴用这个扇形卷成的圆锥的高为 15厘米,圆锥的侧面积为 4π
厘米 2.
16
教材新知精讲
拓展点一
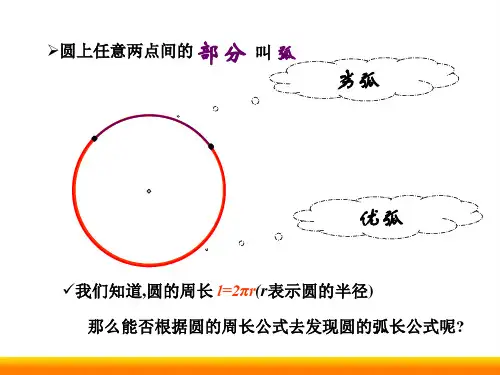
名师解读:(1)在弧长公式中,n 表示 1°的圆心角的倍数,在计算
时,n 和 180 都可以不写单位;
(2)若圆心角的单位不全是度,还有别的单位,例如分和秒,一定
要把分和秒全部转化为度,再进行计算;
π
(3)在弧长公式 l=180中,已知 l,n,r 中的任意两个量可以求出第三
180
180
个量,即 n= π ,r= π ;
180 ,解得r=12.
答案:B
3
教材新知精讲
知识点一
知识点二
综合知识拓展
知识点三
解答这类问题时,一般根据弧长公式直接求解或根据公
式变形求解.
4
教材新知精讲
知识点一
知识点二
综合知识拓展
知识点三
知识点二扇形的面积公式
半径为r的圆中,圆心角为n°的扇形的面积为
π2
S= 360
=
π
×
180 2
分析:先利用弧长公式和扇形的面积公式计算 =
90π·4
=2π,
180
90π×42
扇形 OAB 的面积= 360 =4π,利用扇形的弧长等于圆锥的底面圆的
周长得到 2π·DC=2π,则 DC=1,由扇形的半径等于圆锥的母线长得到
SC=4,然后利用勾股定理可计算出高 SD.

弧长和扇形面积ppt

利用弧度制计算弧长
总结词
利用弧度制计算弧长是一种基于角度的另一种计算方式，通过将角度转换为弧度，并利用弧长公式进行计算。
详细描述
在弧度制下，角度和弧长之间的关系可以用公式L=rθ表示，其中θ是以弧度为单位的角度。通过将角度转换为弧度，我们可以利用这个公式计算出弧长。
利用微积分计算弧长
总结词
利用微积分计算弧长是一种基于微元法的计算方式，通过将圆分割成无数个小的弧段，并求和得到整个圆的周长。
详细描述
利用微积分计算弧长的基本思想是将圆分割成无数个小的弧段，每个弧段的长度可以近似为弦长。然后，将这些弦长相加得到整个圆的周长。这个方法可以用来计算任意曲线的长度，包括圆的周长。
03 扇形面积的计算方法
利用圆的性质计算扇形面积
总结词
通过圆的性质，我们可以将扇形面积转化为圆的一部分，从而计算出其面积。
05 弧长和扇形面积的扩展知识
弧长的变种：曲线的长度
弧长的概念
弧长是曲线的基本属性之一，表示曲线上两点之间的长度。在几何学中，弧长通常用于描述曲线段的长度。
曲线的长度
除了弧长，曲线的长度也是重要的概念。一条曲线由无数个小的直线段组成，这些直线段的长度之和就是曲线的总长度。
计算方法
计算曲线的长度通常需要使用微积分的方法，通过求和公式将无数个小的直线段长度相加，得到曲线的总长度。
04 弧长和扇形面积的应用
在几何学中的应用
弧长公式
弧长公式是计算圆弧或曲线的长度的重要工具，广泛应用于几何学中。通过弧长公式，可以确定圆弧的长度，进而用于解决与圆、椭圆、抛物线等形状相关的几何问题。
扇形面积公式
扇形面积公式是计算扇形面积的基础，对于解决与圆、椭圆、抛物线等形状相关的几何问题具有重要意义。通过扇形面积公式，可以确定扇形的面积，进而用于解决与角度、弧长等相关的几何问题。

弧长和扇形面积第二课时初中数学原创课件

24.4 弧长和扇形面积(2)
复习回顾
1. 半径为 3 的圆中，圆心角为 120 的弧长是 2 ，扇形面积是 3 .
l nR 120 3 2 180 180
S扇形 =
nR2 360
120 32 360
3
复习回顾
2. 半径为 6 的圆中，扇形面积为 9π，则它的弧长为 3 .
S扇形 =
h2 r2 l2.
B
O r A 圆锥的母线长都相等.
圆锥的侧面积和全面积
做一做：沿一条母线将圆锥侧面剪开并展平，观察圆锥的侧面展开图.
圆锥的侧面展开图是扇形.
圆锥的侧面积和全面积
想一想：圆锥的侧面展开图是扇形，那扇形的半径与圆锥中哪一条线段相等，扇形的弧长与谁相等？
圆锥的侧面积和全面积
A 多少 cm？
过圆锥轴（高）的截面，即△ABC
B
C
分析：
曲面平面. 圆锥侧面扇形.
垂线段最短 BD.
BAC 1 BAB '. 2
A
B A
B
D
C
C B'
例题
解：设圆锥侧面展开图的圆心角为 n ，
nl 2r , n r 360 10 360 120.
180
l
30
BAC 60 .
根据垂线段最短，
A
当 BD AC 时 BD 最短.
BD 15 3(cm).
B
B'
D
∴它爬行的最短路线长是15 3 cm. C
练习
3. 已知圆锥底面半径为 10 cm，母线长为 40 cm. 若一甲虫从圆锥底面圆上一点 A 出发，沿着圆锥侧面绕行到母线 PA 的中点 B ，它所走的最短路程长是多少 cm？

弧长及扇形的面积PPT教学课件

O
O
H—HN—CH—C—OH＋ H—HN—CH—C—OH＋
R
R
O
O
H—HN—CH—C—OH＋ H—HN—CH—C—OH ＋
R O
H—HN—CH—C—OH
R 2020/10/4
R
酶
O
—HN—CH—C— ＋ n
nH2O
R
（5）人体必需氨基酸
必需氨基酸:不能在人体内合成，必须由食物供给的氨基酸。
八种成人必需氨基酸：缬氨酸、亮氨酸、异亮氨基酸、赖氨基酸、蛋氨酸、色氨酸、苏氨酸、苯丙氨基酸。
CH2—O—C—R
2020/10/4
动物脂肪与植物油
2020/10/4
不同的油脂性质不同（R不同）
多数动物脂肪因饱和脂肪酸甘油酯含量高在常温下呈固态
植物油因不饱和脂肪酸甘油酯含量高而在常温下呈液态
油脂的生理功能
2020/10/4
油脂为什么能产生热量？
O CH2—O—C—C17H33
O CH —O—CO—C17H33 CH2—O—C—C17H33
2)如果这只够只能绕柱子转过n°角,那么它的最大活动区域有多大?
探索弧长与扇形面积的关系
比较扇形面积(S)公式和弧长(l)公式,你能用弧长来表示扇形的面积吗?
S 1 Rl 2
R
S
n° O
l
例4:扇形AOB的半径12cm,∠AOB=120°,
求弧AB的长(结果精确到0.1cm)和扇形AOB 的面积(结果精确到0.1cm2)
2C17H33COOH + 51O2 氧化酶 34H2O + 36CO2 CH2—OH CH2—OH + 7O2 氧化酶 8H2O + 6CO2 CH2—OH

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

长为__7__. A A1 A2
B
C
圆心角是n0的扇形面积是圆面积的3n60
如果用字母 S 表示扇形的面积， n表示圆心角的度数，r 表示圆半径，那么扇形面积的计算公式是：
S扇形＝
n 360
S圆
＝n
360
πr2
问题：
比较扇形面积计算公式与弧长计算公式，你能用弧长和半径来计算扇形的面积吗？
弧长公式：l nR
S扇形
＝n
360
180 πr2
分别以AB、BC、AC为直
径作3个半圆，求图中阴
影部分的面积
A
F
4．如图，在矩形ABCD中，
BC=2AB，以B为圆心，BC为半
径的圆交AD于E，交BA的延长 A
线于F，设AB=a，求阴影部分
的面积.
B
C
B
E D
C
5.如图，一台机器的大轮⊙O和小轮⊙P外切于点C，且两轮都和板面相切于A、B，若 ⊙O的半径为3cm，⊙P的半径为1cm，求阴影部分的面积.
O D
A
C
B
1. 如图：在△AOC中，∠AOC=900，∠C=150，以O为圆心，AO为半径的圆交AC与B点，若OA=6，求
2.如图，已知P、Q分别是半径为1的半圆圆周上的两个三等分点，AB是直径，求阴影部分的面积 .
P
Q
A
O
B
3．如图，在Rt△ABC中，
AC=4，BC=3，∠C=90°,
弧长及扇形的面积
复习：
1、圆周长为C，半径为R，则C与R的关系是__C____2___r__.
探究一:
1 • 2r
（1）1°的圆心角所对的弧长是____3_6__0___________.
所以：在半径为R的圆中，n°的圆心角所对的弧长
n • 2r
l =__3__6__0________ 1的圆心角 O n的圆心角
为__2_0__,扇形的周长为___32____.
练一练：
5.如图，⊙A、 ⊙B、
⊙C两两不相交，
且半径都是2cm，
图中阴影部分
的面积_____.
B
A C
A
D
B
C
6.如图，线段AB与⊙O相切于点C，连接OA、
OB，OB交⊙O于点D，已知OA=OB=4，
AB= 4 3 ,求(1)⊙O的半径，
(2)图中阴影部分的面积.
C D
1的弧
弧长公式：l nR A
B
180
如下图，由组成圆心角的两条半径和圆心角
所对的弧围成的图形是扇形。
B
弧圆心角 O
A
B
扇形
O A
复习：圆面积S与半径R之间的关系是___S_____r__2___,
圆心角是10的扇形面积是多少？圆心角是10的扇形面积是圆面积的3160
圆心角为n0的扇形面积是多少?
A1
C
B2
A
B C2
A2
2.矩形ABCD的边AB=8，AD=6，现将矩形 ABCD放在直线l上且沿着l向右作无滑动地翻滚，当它翻滚至类似开始的位置时（如图所示），则
顶点A所经过的路线长是1_2________．
3.如图，有一长为8cm，宽为6cm的长方形木板在桌面上做无滑动的翻滚（顺时针方向），木板上顶点A的位置变化为A－A1－A2,其中第二次翻滚被桌面上一小木块挡住，使木板边沿A2C与桌面成30°角，则点A翻滚到A2的位置，经过的路径
S扇形=
1 lR 2
练习： 1.圆弧的半径为4，弧所对的圆心角为60°，
2.则扇弧形长的为弧_长_34_为_,扇5 形面，积圆为心_角_83_为_.90°，则扇形的半径为_1_0__.
3.扇形的面积为 10 ，半径为6，则其
圆心角为__1_0_0__度. 4.扇形半径为6，面积为60，则扇形的弧长
OC
P
AB
小结
1 .弧长、扇形面积公式. 2 .不规则图形的面积的求法：用规则的图形的面积来表示. .
3 .数学思想的应用： ①转化思想. ②整体思想.
• 以下三张暂时不用，时间不够。
典型例题：
1.如图，把直角三角形ABC的斜边AB放在直线上，按顺时针方向在上转动两次，使它转到△A2B2C2的位置上，设BC＝1，AC＝ 3 ，则顶点A运动到A2的位置时，点A经过的路线有多长？点A经过的路线与直线所围成的图形的面积有多大？