180 6
6
α2=750× π = 25π =4π+ π ,
180 6
6
所以α1 在第二象限,α2 在第一象限.
(2)将β 1,β 2用角度制表示,并在-720°~0°范围内找出与它们有相同 终边的所有角.
解:(2)β1= 3π ×( 180 )°=108°,与β1 终边相同的角θ1=k·360°+108°,k∈Z.
(3)在[0°,720°]中找出与 2π 终边相同的角. 5
(3)解:因为 2 π= 2 π×( 180 )°=72°,
55
π
所以与 2π 终边相同的角为θ=72°+k·360°(k∈Z). 5
当 k=0 时,θ=72°; 当 k=1 时,θ=432°, 所以在[0°,720°]中与 2π 终边相同的角为 72°,432°.
5
π
由-720°≤θ1<0°,得-720°≤k·360°+108°<0°,所以 k=-2 或 k=-1. 所以在-720°~0°范围内与β1 有相同终边的角是-612°和-252°.
β2=- 7π ×( 180 )°=-420°,与β2 终边相同的角θ2=k·360°-420°,k∈Z.
3
π
由-720°≤θ2< 0°,
1.1.2 弧度制
课标要求:1.了解弧度制.2.能进行角度与弧度的互化.3.掌握弧度制下 的弧长公式和扇形面积公式.
自主学习
知识探究
1.弧度制
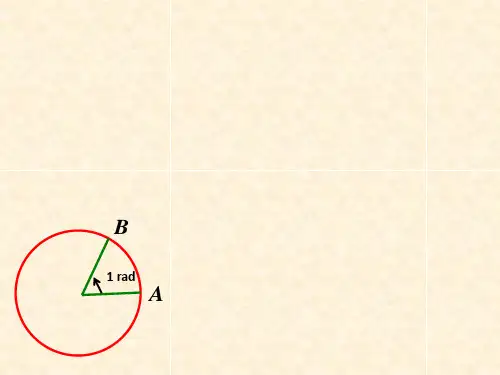
(1)长度等于 半径长 的弧所对的 圆心角 叫做1弧度的角,用符号
rad表示,读作弧度.以弧度作为单位来度量角的单位制叫做弧度制.
(2)任意角的弧度数与实数的对应关系
360