第4讲：怎样用函数描述简谐运动

简谐运动的公式
简谐运动是一种按固定时间周期运行的运动，也是物理
学中经常用到的一种运动形式。

它是由三个物理量共同组成，分别是位置（位置为物体相对于起始点）、速度和加速度，它们之间会有一定的关系。

简谐运动的公式也比较容易推导，可以用x、v、a三个
物理量来表示，其中x表示位置，v表示速度，a表示加速度。

它们之间的关系可以用如下方程式表示：
$$ x(t) = x_0 + v_0 t + \frac{1}{2}a_0 t^2 $$
公式中的参数表示什么？x_0表示的是物体的初始位置，
v_0表示的是物体初始的速度，a_0表示的是物体的初始加速度，t表示的是在运动中衡量出来的时间。

用简谐运动的公式可以很容易推导出物体在一个定义域
内的运动规律，并且可以用它模拟各种变化的运动轨迹，例如物体从速度为v_0加速度为a_0的开始状态，可以模拟出物体在各种不同时间段后的位置，总结起来也比较简单：
在简谐运动中，物体的位置x随时间的变化满足一定的
公式：
x(t) = x_0 + v_0 t + \frac{1}{2}a_0 t^2
其中x_0、v_0、a_0都是物体在起始状态的物理量，t表示物体在定义域内所衡量出来的时间，通过该公式可以可以很容易推导出物体在定义域内的运动。

简谐运动的描述知识集结知识元简谐运动的振幅、周期和频率知识讲解2．相关物理量：①振幅A：振动物体离开平衡位置的最大距离。

②周期T：做简谐运动的物体完成一次全振动所需要的时间。

③频率f：单位时间内完成全振动的次数。

④相位：描述周期性运动在各个时刻所处的不同状态。

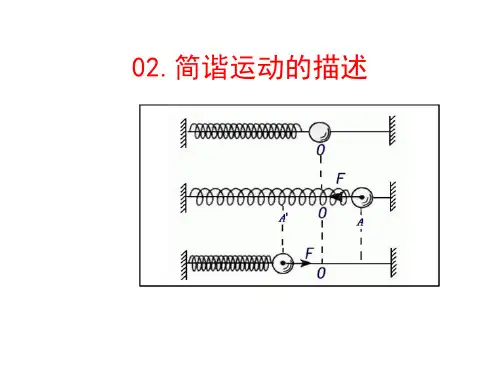
3．受力特征：①做简谐运动的质点受到的力与它偏离平衡位置位移的大小成正比，并且总是指向平衡位置，通常将这种力称为回复力。

②回复力：F=-kx③若质点受到的回复力为F=-kx，则质点的运动为简谐运动。

4．运动特征位移x：方向始终背离平衡位置，每经过平衡位置位移方向发生改变；远离平衡位置时位移增大，靠近平衡位置时位移减小。

速度v：每经过最大距离处速度方向发生改变，远离平衡位置时速度方向和位移方向相同，靠近平衡位置时速度方向和位移方向相反。

加速度，方向与位移方向相反，总指向平衡位置．简谐运动是一种变加速运动．在平衡位置时，速度最大，加速度为零；在最大位移处，速度为零，加速度最大。

5．振动能量简谐运动过程中动能和势能相互转化，机械能守恒．振动能量与振幅有关，振幅越大，能量越大。

6．周期性：简谐运动是一种复杂的非匀变速运动，要结合牛顿运动定律、动量定理、动能定理、机械能守恒定律来分析解决简谐运动的问题。

（1）简谐运动的对称性：振动物体在振动的过程中，在关于平衡位置对称的位置上，描述物体振动状态的物理量（位移、速度、加速度、动量、动能、势能等）大小相等。

（2）简谐运动的周期性：振动物体完成一次全振动（或振动经过一个周期），描述物体振动状态的物理量（位移、速度、加速度、动量、动能、势能等）又恢复到和原来一样。

简谐运动的周期是由振动系统的特性决定的，与振幅无关。

弹簧振子的周期只决定于弹簧的劲度系数和振子的质量，与其放置的环境和方式无关。

例题精讲简谐运动的振幅、周期和频率例1.如图所示，一质点在x轴上以O为平衡位置做简谐运动，其振幅为8cm，周期为4s。

t=0时物体在x=4cm处，向x轴负方向运动，则（）A．质点在t=1.0s时所处的位置为x=+4cmB．质点在t=1.0s时所处的位置为x=-4cmC．由起始位置运动到x=-4cm处所需的最短时间为sD．由起始位罝运动到x=-4cm处所需的最短时间为s例2.如图所示，一质点在平衡位置O点附近做简谐运动，若从质点通过O点时开始计时，经过0.9s质点第一次通过M点，再继续运动，又经过0.6s质点第二次通过M点，该质点第三次通过M点需再经过的时间可能是（）A．1s B．1.2s C．2.4s D．4.2s例3.如图1所示，弹簧振子以O点为平衡位置，在A、B两点之间做简谐运动。

简谐运动表达式
简谐运动是一种重要的物理现象，它描述了在恢复力作用下，质点沿着直线或曲线作谐振运动的过程。

简谐运动的数学表达式可以使用正弦或余弦函数来表示，通过以下公式进行描述：
$ x(t) = A \times \cos(\omega t + \phi) $
其中，$ x(t) $ 是质点在时间 $ t $ 时的位移，$ A $ 是振幅，$ \omega $ 是角频率，$ \phi $ 是初相位。

在这个表达式中，振幅 $ A $ 表示了简谐运动的最大位移，角频率 $ \omega $ 则代表了单位时间内变化的相位角度。

初相位 $ \phi $ 反映了质点在 $ t=0 $ 时刻的初始位置。

简谐运动的表达式还可以通过正弦函数表示，具体形式如下：
$ x(t) = A \times \sin(\omega t + \phi) $
与余弦函数表示法相比，正弦函数表示法在初始位移上有所不同，但本质是相同的。

简谐运动的表达式不仅适用于描述单摆、弹簧振子等机械振动系统，也能有效描绘声波、光波等波动现象。

通过这一简洁的数学表达式，我们能够更深入地理解和分析复杂的振动运动规律。

总的来说，简谐运动表达式是物理学中重要的数学工具，它通过简单的公式形式，展现了自然界中许多周期性运动现象的共性特征，为我们解释和预测自然现象提供了重要参考。

简谐运动的公式和定义一、简谐运动的公式和定义1、公式：$x=A\sin(ωt+φ)$2、公式中的参数：（1）式中$x$表示振动质点相对于平衡位置的位移，t表示振动的时间。

（2）A表示振动质点偏离平衡位置的最大距离，即振幅。

（3）ω称为简谐运动的圆频率，它也表示简谐运动物体振动的快慢。

3、定义：如果质点所受的力与它偏离平衡位置位移的大小成正比，并且总是指向平衡位置，质点的运动就是简谐运动。

4、特点：（1）简谐运动是最基本、最简单的振动。

（2）简谐运动的位移随时间按正弦规律变化，所以它不是匀变速运动，应为变力作用下的变加速运动。

5、特征：（1）受力特征：回复力$F=-kx$，$F$（或$a$）的大小与$x$的大小成正比，方向相反。

（2）运动特征：靠近平衡位置时，$a、F、x$都减小，$v$增大；远离平衡位置时，$a、F、x$都增大，$v$减小。

（3）能量特征：振幅越大，能量越大。

在运动过程中，动能和势能相互转化，系统的机械能守恒。

（4）周期性特征：质点的位移、回复力、加速度和速度均随时间做周期性变化，变化周期就是简谐运动的周期$T$；动能和势能也随时间做周期性变化，其变化周期为$\frac{T}{2}$。

（5）对称性特征：关于平衡位置$O$对称的两点，加速度的大小、速度的大小、动能、势能相等，相对平衡位置的位移大小相等。

6、平衡位置：物体在振动过程中回复力为零的位置。

7、回复力的定义：使物体返回到平衡位置的力。

8、回复力的方向：总是指向平衡位置。

9、回复力的来源：属于效果力，可以是某一个力，也可以是几个力的合力或某个力的分力。

二、简谐运动的相关例题（多选）关于简谐运动以及做简谐运动的物体完成一次全振动的意义，以下说法正确的是____A．位移减小时，加速度减小，速度增大B．位移的方向总跟加速度的方向相反，跟速度的方向相同C．动能或势能第一次恢复为原来的大小所经历的过程D．速度和加速度第一次同时恢复为原来的大小和方向所经历的过程E．物体运动方向指向平衡位置时，速度的方向与位移的方向相反；背离平衡位置时，速度方向与位移方向相同答案：ADE解析：当位移减小时，回复力减小，则加速度减小，物体向平衡位置运动，速度增大，故A正确；回复力与位移方向相反，故加速度和位移方向相反，但速度与位移方向可以相同，也可以相反；物体运动方向指向平衡位置时，速度的方向与位移的方向相反；背离平衡位置时，速度方向与位移方向相同，故B错误，E正确；一次全振动，动能和势能可以多次恢复为原来的大小，故C错误；速度和加速度第一次同时恢复为原来的大小和方向所经历的过程为一次全振动，故D正确。

第4讲简谐运动、简谐运动的表达式及其图象【基本概念与基本规律】一、简谐运动定义1．机械振动物体在平衡位置附近所做的往复运动叫机械振动。

机械振动的条件是：（1）物体受到回复力的作用；（2）阻力足够小。

2．回复力使振动物体返回平衡位置的力叫回复力。

回复力时刻指向平衡位置。

回复力是以效果命名的力，它是振动物体在振动方向上的合外力，可能是几个力的合力，也可能是某个力或某个力的分力，可能是重力、弹力、摩擦力、电场力、磁场力等。

3．简谐运动物体在跟偏离平衡位置的位移大小成正比，并且总指向平衡位置的回复力作用下的振动，叫简谐运动。

表达式为：F＝－kx。

4．描述简谐运动的物理量（1）位移x：由平衡位置指向振子所在处的有向线段，最大值等于振幅；（2）振幅A：是描述振动强弱的物理量。

（一定要将振幅跟位移相区别，在简谐运动的振动过程中，振幅是不变的，而位移是时刻在改变的）（3）周期T：是描述振动快慢的物理量。

频率f＝T 1。

【例1】下列属于机械振动选择完整的是（）①乒乓球在地面上的来回上下运动；②弹簧振子在竖直方向的上下运动；③秋千在空中来回的运动；④竖于水面上的圆柱形玻璃瓶上下振动A．①②B．②③C．③④D．②③④。

【例2】关于简谐运动回复力的说法正确的是（）A．回复力F=−kx中的x是指振子相对于平衡位置的位移。

B．回复力F=−kx中的x是指振子从初位置指向末位置的位移 C．振子的回复力一定就是它所受的合力 D．振子的回复力一定是恒力【例3】关于简谐运动的位移、速度、加速度的关系，下列说法中正确的是（）A．位移减小时，加速度增大，速度增大 B．位移方向总跟加速度方向相反，跟速度方向相同 C．物体运动方向指向平衡位置时，速度方向跟位移方向相反。

D．物体向平衡位置运动时，做加速运动，背离平衡位置时，做减速运动。

~ 第 1 页 ~【例4】如图所示，一个弹簧振子沿x轴在B、C间做简谐运动，O为平衡位置，当振子从B点向O 点运动经过P点时振子的位移为，振子的回复力为，振子速度为，振子的加速度为（填“正”“负”或“零”）图 1二、理解简谐运动重难点1．平衡位置的理解平衡位置是做机械振动物体最终停止振动后振子所在的位置，也是振动过程中回复力为零的位置。

简谐运动表达式
简谐运动是物理学里面一种重要的运动模型，它可以用来描述某些运动物体受到力的作用下所产生的特定移动变化。

它数学上的表达式是F=ma，其中F表示运动物体的受力大小，m表示物体的质量，而a则表示物体在这个力的作用下所受的加速度。

由此可见，简谐运动就是当某个物体受到一定大小的力时，它就会产生一定规律的移动变化，这种规律性的变化就是简谐运动。

简谐运动在物理学中有着非常重要的意义，它可以用来描述不同的运动系统。

比如它可以用来解释传统的摆动运动模型，这是由受力而产生的特定移动轨迹，可以用来描述卫星在太空中的运动轨迹，以及可以用来描述一枚弹簧的振动等等，这些移动物体都可以通过简谐运动模型来描述。

简谐运动不仅可以用来描述不同的物理运动系统，而且还能广泛地应用到生活当中去。

比如当我们在街边看到一个小朋友挥舞着滑板板在滑行时，他运动的过程能够被拟合出正弦曲线，看得出来这也是一种简谐运动，另外当我们玩滑翔伞时，其实也是在进行简谐运动，当你在钢丝索上滑行时，也会受到不同的外力，而这力的作用下你的运动轨迹也会符合简谐运动模型。

简谐运动在人们的生活中涉及面非常广泛，它不仅可以帮助我们理解环境中的运动性质，而且还可以帮助人们形成对物理支配的重要认知，以及对日常生活中种种运动行为和背后机制的深入理解。

总之，简谐运动是物理学里面一种重要、基本的运动模型，它可以用来描述某些物体受力而移动时的特定规律，这种规律性的变化及其涉及到的内容，在物理学中具有重要的理论意义，也在实际生活中有着广泛的应用。