如何描述简谐运动呢

《简谐运动》知识清单一、什么是简谐运动简谐运动是一种理想化的机械运动模型。

它的定义是：如果一个物体所受到的力跟它偏离平衡位置的位移大小成正比，并且力的方向总是指向平衡位置，那么这个物体的运动就叫做简谐运动。

比如常见的弹簧振子，就是一种典型的简谐运动。

当弹簧一端固定，另一端连接一个物体，将物体拉离平衡位置后释放，它就会在平衡位置附近做往复运动，这种运动就是简谐运动。

二、简谐运动的特点1、受力特点物体所受的回复力F 与位移x 大小成正比，方向相反，即F ＝kx，其中 k 是比例系数，叫做回复力系数。

回复力是使物体回到平衡位置的力。

在弹簧振子中，回复力就是弹簧的弹力；在单摆中，回复力是重力沿圆弧切线方向的分力。

2、运动特点简谐运动是一种周期性运动，具有重复性和对称性。

（1）重复性：物体在相同的时间间隔内，重复相同的运动状态。

（2）对称性：关于平衡位置对称的两点，速度大小相等、方向相反；加速度大小相等、方向相反；位移大小相等、方向相反。

3、能量特点在简谐运动中，系统的机械能守恒。

当物体远离平衡位置时，动能减小，势能增大；当物体靠近平衡位置时，动能增大，势能减小。

但总的机械能保持不变。

三、简谐运动的表达式简谐运动的位移时间关系可以用正弦函数或余弦函数来表示：x ＝A sin(ωt ＋φ) 或 x ＝A cos(ωt ＋φ)其中，A 表示振幅，是物体离开平衡位置的最大距离；ω 是角频率，ω ＝2π/T，T 是周期；φ 是初相位，决定了运动的初始状态。

四、简谐运动的周期和频率1、周期完成一次全振动所需要的时间叫做周期，用 T 表示。

周期的大小由振动系统本身的性质决定，与振幅无关。

对于弹簧振子，T ＝2π√（m/k)，其中 m 是振子的质量，k 是弹簧的劲度系数。

对于单摆，T ＝2π√（L/g)，其中 L 是摆长，g 是重力加速度。

2、频率单位时间内完成全振动的次数叫做频率，用 f 表示。

频率与周期互为倒数，即 f ＝ 1/T。

简谐运动的描述引言简谐运动是物理学中一种重要的运动形式，它在自然界和工程领域中都有广泛的应用。

本文将对简谐运动进行详细描述，并深入探讨其特征、数学表达以及应用。

定义简谐运动是一种周期性运动，其特点是运动体沿着某个轴线上往复振动，并且振动的加速度与位移成正比，且恒定。

在简谐运动中，运动体会围绕平衡位置作周期性的振动，如弹簧振子、摆锤等。

特征简谐运动有以下几个主要特征：1.振幅（Amplitude）：振幅是指运动体离开平衡位置的最大位移。

它决定了简谐运动的最大振幅。

2.周期（Period）：周期是指运动体完成一次完整振动所需的时间。

它与频率的倒数成正比，可以用公式T = 1/f来表示，其中T代表周期，f代表频率。

3.频率（Frequency）：频率是指运动体单位时间内振动的次数。

它与周期的倒数成正比，可以用公式f = 1/T来表示，其中f代表频率，T代表周期。

4.相位（Phase）：相位是指简谐运动的偏移值，用角度来度量。

在简谐运动中，相位角随时间而变化，可以用公式θ = ωt来表示，其中θ代表相位角，ω代表角频率，t代表时间。

5.动能和势能：在简谐运动中，运动体会交替转化为动能和势能。

当运动体离开平衡位置时，具有最大位移和最大动能；当运动体接近平衡位置时，具有最小位移和最小动能，但具有最大势能。

数学表达简谐运动的数学表达可以通过以下公式得到：1.位移（Displacement）：\[x(t) = A \cos(\omega t + \phi)\] 其中，x代表位移，A代表振幅，ω代表角频率（ω = 2πf），t代表时间，φ代表相位角。

2.速度（Velocity）：\[v(t) = -A \omega \sin(\omega t + \phi)\] 其中，v代表速度，A代表振幅，ω代表角频率（ω = 2πf），t代表时间，φ代表相位角。

3.加速度（Acceleration）：\[a(t) = -A \omega^2 \cos(\omega t + \phi)\] 其中，a代表加速度，A代表振幅，ω代表角频率（ω = 2πf），t代表时间，φ代表相位角。

简谐运动运动方程
简谐运动是指物体在受到一定形式的外力作用下，做周期性的振动，其运动状态可以用简谐运动方程来描述。

简谐运动方程的一般形式为：
x = A sin(ωt + φ)
其中，x表示物体的位移，A表示振幅，ω表示角频率，t表示时间，φ表示初始相位。

这个方程描述了物体在一条直线上以振幅为A、角频率为ω的周期性振动。

简谐运动方程的特点是周期性、有固定的振幅和角频率，并且它们之间有一定的数学关系，如振幅和角频率之间的关系为：ω = 2πf = 2π/T
其中f表示频率，T表示周期。

简谐运动的周期是一个固定值，与振幅和角频率无关。

简谐运动具有周期性、可叠加性和共振现象等特点，是物理学中的基础概念之一，被广泛应用于各个领域中。

- 1 -。

简谐运动的描述一、简谐运动的概念和特征简谐运动是一种重要的周期性运动，它可以在自然界和人-made系统中观察到。

简谐运动的特征包括：1.周期性：简谐运动是一个重复的过程，物体会在规律的时间间隔内重复相同的运动。

2.能量守恒：简谐运动中物体的总能量保持不变，由动能和势能相互转化，但总能量始终保持恒定。

3.线性回复：简谐运动中，物体的回复力与它的偏离程度成正比，且方向相反，符合胡克定律。

4.最大回复力和最大速度的时刻不一致：简谐运动中，最大回复力与最大速度不会同时发生，它们的时刻相差1/4个周期。

二、简谐运动的数学描述简谐运动可以使用如下的数学描述：一维简谐运动的位移-时间关系：x=Acos(ωt+ϕ)其中， - A为振幅，表示物体偏离平衡位置的最大距离。

- ω为角频率，表示单位时间内的相位变化量。

- t为时间。

- φ为初相位，表示在t=0时刻的位相。

一维简谐运动的速度-时间关系：v=−ωAsin(ωt+ϕ)一维简谐运动的加速度-时间关系：a=−ω2Acos(ωt+ϕ)三、简谐运动的力学模型简谐运动可以通过一维弹簧振子来进行力学建模。

弹簧振子由一个弹簧和一个质量块组成。

当质量块受到外力扰动后，它会围绕平衡位置做简谐振动。

1.弹簧的自由长度为L，当质量块偏离平衡位置时，弹簧受到回复力，使得质量块回到平衡位置。

2.弹簧回复力与质量块的偏离程度成正比，符合胡克定律：F=−kx其中， - F为回复力的大小。

- k为弹簧的劲度系数，描述了弹簧的刚度和回复力的大小。

- x为质量块偏离平衡位置的距离。

四、简谐运动的频率和周期简谐运动的频率和周期和与力学模型中的角频率相关。

频率：简谐运动的频率表示单位时间内完成一个完整周期的次数，用hertz（Hz）作为单位，频率等于角频率除以2π。

周期：简谐运动的周期表示完成一个完整周期所需要的时间，用秒（s）作为单位，周期等于角频率的倒数。

五、简谐运动的实际应用简谐运动是自然界和人-made系统中普遍存在的一种运动形式，其应用十分广泛。

简谐运动的描述简谐运动的描述简谐运动是指一个物体在一个恒定的力场中做周期性的振动。

它是一种特殊的振动，具有周期性、稳定性和可预测性等特点。

简谐运动在自然界和工业生产中都有广泛应用，如弹簧振子、钟摆、电磁波等。

一、简谐运动的基本概念1.1 振幅振幅是指简谐运动中物体从平衡位置最大偏离距离。

通常用字母A表示，单位为米（m）。

1.2 周期周期是指简谐运动中物体完成一次完整振动所需要的时间。

通常用字母T表示，单位为秒（s）。

1.3 频率频率是指单位时间内完成的振动次数。

通常用字母f表示，单位为赫兹（Hz）。

1.4 相位相位是指在同一时刻内处于不同状态的两个物体之间的时间差。

相位差可以用角度来表示，通常用字母Φ表示。

二、简谐运动的数学描述2.1 速度与加速度公式对于简谐运动而言，速度和加速度分别可以用以下公式来计算：v = Aωcos(ωt + Φ)a = -Aω^2sin(ωt + Φ)其中，ω为角速度，可以用以下公式计算：ω = 2πf2.2 位移公式对于简谐运动而言，物体的位移可以用以下公式来计算：x = Acos(ωt + Φ)其中，A为振幅，Φ为相位差。

三、简谐运动的特点3.1 周期性简谐运动具有周期性，即物体在恒定的力场中做周期性的振动。

物体完成一次完整振动所需要的时间是固定的。

3.2 稳定性简谐运动具有稳定性，即物体在恒定的力场中做周期性的振动时，其运动状态是稳定并可预测的。

3.3 可预测性由于简谐运动具有稳定性和周期性，因此可以精确地预测物体在未来某一时刻所处的位置、速度和加速度等状态。

四、简谐运动的应用4.1 弹簧振子弹簧振子是一种常见的简谐振动系统。

它由一个质量和一个弹簧组成，在重力作用下进行周期性振动。

弹簧振子广泛应用于工业生产中的测量和控制系统中。

4.2 钟摆钟摆是一种通过重力驱动的简谐振动系统。

它由一个重物和一个支架组成，在重力作用下进行周期性振动。

钟摆广泛应用于时间测量、科学研究和导航等领域。

简谐运动的特点或规律
1. 简谐运动那可是有周期性的呀！就像钟摆一样，来回摆动，总在重复着相同的模式，这难道不神奇吗？钟摆就是很好的例子呀，滴答滴答，有规律地摆动着。

2. 它的位移和回复力之间有着紧密的联系呢！你想想弹簧，拉伸或压缩后，它总会努力回到原来的位置，这多么有趣呀！就如同我们努力追求最初的状态一样。

3. 简谐运动还有一个特点，就是它的能量会在动能和势能之间转换哦！如同跷跷板一样，这边高了那边就低了，是不是很有意思呀？想想看，动能势能来回变，多奇妙呀！
4. 其振动的幅度也是相对稳定的哟！好比跳绳时，绳子摆动的幅度大致是固定的，不会突然变得超大或超小呢，这就是简谐运动的特点呀。

5. 而且简谐运动的频率也是很关键的呢！如同心跳，有自己稳定的频率，不快也不慢。

要是心跳乱了频率，那可就糟糕啦，简谐运动也是这样有规律呢！
6. 简谐运动的平衡位置至关重要呀！这就好像是我们的家一样，是个中心，来来去去都围绕着它，是不是很特别呢？
7. 它的振动过程是那么的有规律，让人惊叹！就像四季更替一样，春去秋来，年年如此，简谐运动也是有着自己独特的“节奏”呢！
8. 哇塞，简谐运动真的太有意思啦！它的这些特点和规律，让我们看到了自然界中这么多美妙又神奇的现象呀！
我的观点结论就是：简谐运动有着许多独特又神奇的特点和规律，深入了解它真的非常有趣和有意义！。

第三节简谐运动的公式描述简谐运动是一种特殊的周期性运动，它的公式描述可以使用正弦函数或者余弦函数来表示。

在简谐运动中，物体围绕平衡位置以固定的频率振动，振动的幅度保持不变，且运动轨迹为周期性的。

简谐运动的公式描述有以下几种形式：1. 位移公式：x(t) = A * cos(ωt + φ)其中，x(t)代表物体在时间t时刻的位移，A为振幅，ω为角频率，t为时间，φ为初相位。

2. 速度公式：v(t) = -A * ω * sin(ωt + φ)其中，v(t)代表物体在时间t时刻的速度。

3. 加速度公式：a(t) = -A * ω^2 * cos(ωt + φ)其中，a(t)代表物体在时间t时刻的加速度。

在上述的公式中，振幅A代表物体的最大位移，角频率ω代表单位时间内振动的周期数，初相位φ则决定了物体振动的起始位置。

通过这些公式，我们可以描述简谐运动的各种特性。

首先，振幅A决定了物体在简谐运动中的最大位移。

振幅越大，表示物体振动的幅度越大；振幅越小，表示物体振动的幅度越小。

其次，角频率ω决定了振动的频率，即单位时间内振动的周期数。

角频率越大，表示物体振动的频率越高；角频率越小，表示物体振动的频率越低。

初相位φ则决定了物体振动的起始位置。

当φ为零时，物体在平衡位置开始振动；当φ不为零时，物体将在偏离平衡位置的位置开始振动。

速度公式和加速度公式则描述了物体在简谐运动中的速度和加速度变化情况。

速度公式表明，在简谐运动中，物体的速度是按照正弦函数的形式进行变化的；加速度公式则表明，在简谐运动中，物体的加速度是按照余弦函数的形式进行变化的。

简谐运动的公式描述可以通过实验观察数据和理论推导得到。

在实验中，我们可以测量物体的运动轨迹、位移、速度和加速度，并通过这些数据来计算振幅、角频率和初相位等参数。

而在理论推导中，我们可以通过运动方程以及牛顿第二定律等原理，推导出简谐运动的公式描述。

总之，简谐运动的公式描述为x(t) = A * cos(ωt + φ)，其中x(t)为位移，A为振幅，ω为角频率，t为时间，φ为初相位。

简谐运动的公式和定义一、简谐运动的公式和定义1、公式：$x=A\sin(ωt+φ)$2、公式中的参数：（1）式中$x$表示振动质点相对于平衡位置的位移，t表示振动的时间。

（2）A表示振动质点偏离平衡位置的最大距离，即振幅。

（3）ω称为简谐运动的圆频率，它也表示简谐运动物体振动的快慢。

3、定义：如果质点所受的力与它偏离平衡位置位移的大小成正比，并且总是指向平衡位置，质点的运动就是简谐运动。

4、特点：（1）简谐运动是最基本、最简单的振动。

（2）简谐运动的位移随时间按正弦规律变化，所以它不是匀变速运动，应为变力作用下的变加速运动。

5、特征：（1）受力特征：回复力$F=-kx$，$F$（或$a$）的大小与$x$的大小成正比，方向相反。

（2）运动特征：靠近平衡位置时，$a、F、x$都减小，$v$增大；远离平衡位置时，$a、F、x$都增大，$v$减小。

（3）能量特征：振幅越大，能量越大。

在运动过程中，动能和势能相互转化，系统的机械能守恒。

（4）周期性特征：质点的位移、回复力、加速度和速度均随时间做周期性变化，变化周期就是简谐运动的周期$T$；动能和势能也随时间做周期性变化，其变化周期为$\frac{T}{2}$。

（5）对称性特征：关于平衡位置$O$对称的两点，加速度的大小、速度的大小、动能、势能相等，相对平衡位置的位移大小相等。

6、平衡位置：物体在振动过程中回复力为零的位置。

7、回复力的定义：使物体返回到平衡位置的力。

8、回复力的方向：总是指向平衡位置。

9、回复力的来源：属于效果力，可以是某一个力，也可以是几个力的合力或某个力的分力。

二、简谐运动的相关例题（多选）关于简谐运动以及做简谐运动的物体完成一次全振动的意义，以下说法正确的是____A．位移减小时，加速度减小，速度增大B．位移的方向总跟加速度的方向相反，跟速度的方向相同C．动能或势能第一次恢复为原来的大小所经历的过程D．速度和加速度第一次同时恢复为原来的大小和方向所经历的过程E．物体运动方向指向平衡位置时，速度的方向与位移的方向相反；背离平衡位置时，速度方向与位移方向相同答案：ADE解析：当位移减小时，回复力减小，则加速度减小，物体向平衡位置运动，速度增大，故A正确；回复力与位移方向相反，故加速度和位移方向相反，但速度与位移方向可以相同，也可以相反；物体运动方向指向平衡位置时，速度的方向与位移的方向相反；背离平衡位置时，速度方向与位移方向相同，故B错误，E正确；一次全振动，动能和势能可以多次恢复为原来的大小，故C错误；速度和加速度第一次同时恢复为原来的大小和方向所经历的过程为一次全振动，故D正确。

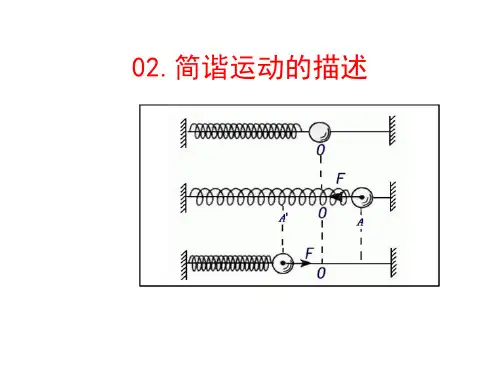
2 简谐运动的描述一、描述简谐运动的物理量1.振幅：振动物体离开平衡位置的最大距离.2.全振动(如图1所示)图1类似于O →B →O →C →O 的一个完整的振动过程. 3.周期和频率 (1)周期①定义：做简谐运动的物体完成一次全振动所需要的时间. ②单位：国际单位是秒(s). (2)频率①定义：单位时间内完成全振动的次数. ②单位：赫兹(Hz). (3)T 和f 的关系：T ＝1f .4.相位描述周期性运动在各个时刻所处的不同状态. 二、简谐运动的表达式简谐运动的一般表达式为x ＝A sin(ωt ＋φ).1.x 表示振动物体相对于平衡位置的位移；t 表示时间.2.A 表示简谐运动的振幅.3.ω叫做简谐运动的“圆频率”，表示简谐运动的快慢，ω＝2πT＝2πf (与周期T 和频率f 的关系). 4.ωt ＋φ代表简谐运动的相位，φ表示t ＝0时的相位，叫做初相位(或初相). 5.相位差若两个简谐运动的表达式为x 1＝A 1sin(ωt ＋φ1)，x 2＝A 2sin(ωt ＋φ2)，则相位差为 Δφ＝(ωt ＋φ2)－(ωt ＋φ1)＝φ2－φ1.一、描述简谐运动的物理量 1.对全振动的理解(1)全振动的定义：振动物体以相同的速度相继通过同一位置所经历的过程，称为一次全振动. (2)全振动的四个特征：①物理量特征：位移(x )、加速度(a )、速度(v )三者第一次同时与初始状态相同. ②时间特征：历时一个周期. ③路程特征：振幅的4倍. ④相位特征：增加2π. 2.对周期和频率的理解(1)周期(T )和频率(f )都是标量，反映了振动的快慢，T ＝1f ，即周期越大，频率越小，振动越慢.(2)一个振动系统的周期、频率由振动系统决定，与振幅无关. 3.对振幅的理解(1)振动物体离开平衡位置的最大距离. (2)振幅与位移的区别 ①振幅等于最大位移的数值.②对于一个给定的振动，振动物体的位移是时刻变化的，但振幅是不变的. ③位移是矢量，振幅是标量. (3)路程与振幅的关系①振动物体在一个周期内的路程为四个振幅. ②振动物体在半个周期内的路程为两个振幅. ③振动物体在14个周期内的路程不一定等于一个振幅.例1 如图2所示，将弹簧振子从平衡位置下拉一段距离Δx ，释放后振子在A 、B 间振动，且AB ＝20 cm ，振子由A 首次到B 的时间为0.1 s ，求：图2 (1)振子振动的振幅、周期和频率； (2)振子由A 到O 的时间；(3)振子在5 s 内通过的路程及偏离平衡位置的位移大小.例2 (多选)(2018·嘉兴市高二第一学期期末)如图3所示为一质点的振动图象，曲线满足正弦变化规律，则下列说法中正确的是( )图3 A.该振动为简谐振动 B.该振动的振幅为10 cmC.质点在前0.12 s 内通过的路程为20 cmD.0.04 s 末，质点的振动方向沿x 轴负方向二、简谐运动表达式的理解2.从表达式x ＝A sin (ωt ＋φ)体会简谐运动的周期性.当Δφ＝(ωt 2＋φ)－(ωt 1＋φ)＝2n π时，Δt ＝2n πω＝nT ，振子位移相同，每经过周期T 完成一次全振动.3.从表达式x ＝A sin (ωt ＋φ)体会特殊点的值.当(ωt ＋φ)等于2n π＋π2时，sin (ωt ＋φ)＝1，即x ＝A ；当(ωt ＋φ)等于2n π＋3π2时，sin (ωt ＋φ)＝－1，即x ＝－A ；当(ωt ＋φ)等于n π时，sin (ωt ＋φ)＝0，即x ＝0.例3 (多选)一弹簧振子A 的位移x 随时间t 变化的关系式为x ＝0.1sin 2.5πt ，位移x 的单位为m ，时间t 的单位为s.则( )A.弹簧振子的振幅为0.2 mB.弹簧振子的周期为1.25 sC.在t ＝0.2 s 时，振子的运动速度为零D.若另一弹簧振子B 的位移x 随时间t 变化的关系式为x ＝0.2sin (2.5πt ＋π4)，则A 滞后B π4三、简谐运动的周期性和对称性 如图4所示图4(1)时间的对称①物体来回通过相同两点间的时间相等，即t DB ＝t BD .②物体经过关于平衡位置对称的等长的两线段的时间相等，图中t OB ＝t BO ＝t OA ＝t AO ，t OD ＝t DO ＝t OC ＝t CO . (2)速度的对称①物体连续两次经过同一点(如D 点)的速度大小相等，方向相反.②物体经过关于O 点对称的两点(如C 与D )时，速度大小相等，方向可能相同，也可能相反. (3)位移的对称①物体经过同一点(如C 点)时，位移相同.②物体经过关于O 点对称的两点(如C 与D )时，位移大小相等、方向相反.利用简谐运动图像理解简谐运动的对称性(1)相隔Δt ＝⎝ ⎛⎭⎪⎫n ＋12T (n ＝0,1,2，…)的两个时刻，弹簧振子的位置关于平衡位置对称，位移等大反向，速度也等大反向。