北师大版六年级下册比和比例复习

六年级下册数学教案总复习比与比例复习课｜北师大版教学目标1. 知识与技能：使学生理解和掌握比与比例的概念，能熟练运用比与比例的知识解决实际问题。

2. 过程与方法：通过问题解决，培养学生的逻辑思维能力和解决实际问题的能力。

3. 情感态度与价值观：激发学生对数学学习的兴趣，培养学生合作交流、自主探究的学习习惯。

教学内容1. 比与比例的概念：复习比与比例的定义，理解比与比例之间的关系。

2. 比与比例的性质：掌握比与比例的基本性质，能运用性质解决实际问题。

3. 比与比例的应用：运用比与比例的知识解决生活中的实际问题。

教学重点与难点重点：比与比例的概念及其性质，比与比例的应用。

难点：比与比例的性质的理解和应用，解决实际问题。

教具与学具准备1. 教具：PPT、教学视频、黑板2. 学具：练习本、笔教学过程1. 导入：通过PPT展示生活中的比与比例实例，引发学生对比与比例的思考。

2. 探究：让学生分组讨论，探究比与比例的性质和应用。

3. 讲解：根据学生的讨论结果，讲解比与比例的概念、性质和应用。

4. 练习：通过课堂练习，让学生巩固比与比例的知识。

板书设计1. 比与比例复习课2. 提纲：比与比例的概念、性质、应用3. 重点内容：比与比例的性质和应用实例作业设计1. 书面作业：完成练习册中的比与比例相关题目。

2. 实践作业：观察生活中的比与比例实例，记录下来并进行分析。

课后反思本节课通过生动的实例导入，激发了学生的学习兴趣。

通过分组讨论和探究，培养了学生的合作精神和解决问题的能力。

通过讲解和练习，使学生对比与比例有了更深入的理解。

总体来说，教学效果良好，但还需在课后通过作业和实践进一步巩固学生的学习成果。

重点关注的细节：教学过程1. 导入阶段：情境创设：利用PPT展示生活中常见的比例关系，如烹饪中食材的比例、家庭成员年龄的比例等，让学生直观感受到比例在生活中的应用，从而引起学生的兴趣。

问题引导：提出引导性问题，如“你们在生活中遇到过比例吗？能举个例子吗？”这样的问题可以促使学生主动思考，将生活实际与数学知识联系起来。

六年级下册数学教案-总复习比与比例复习课|北师大版一、教学目标1.知识目标：通过本节课的学习，学生应该达到以下目标：–能够掌握比和比例的概念并熟练运用；–能够解决实际问题时运用比和比例相应的计算方法；–能够准确地理解和使用比例的性质和定理。

2.技能目标：通过本节课的学习，学生应该能够：–运用比和比例的概念、计算方法和性质解决实际问题；–整理并整体把握比和比例相关知识点和技能。

3.情感目标：通过本节课的学习，学生应该能够：–培养学生的数学思维和分析问题的能力；–提高学生对数学知识的兴趣和探究乐趣。

二、教学重难点分析1.教学重点：比和比例的掌握和运用、比例的性质和定理的理解和应用。

2.教学难点：比例的难点是对比例性质和定理的深入理解和应用。

三、教学过程1.导入环节通过提问引入本节课的主题，让学生概念比和比例的相关知识点，以便将学生的思路引导到正确的方向上。

2.知识讲解•比和比例的概念；•比和比例的运用；•比例的性质和定理。

3.练习环节1.单项选择题；2.填空题；3.计算题；4.应用题；5.综合题。

4.小结与反思本节课须进行小结与反思，梳理学生已掌握的知识和技能，以及未掌握的知识点和技能，并为下节课的知识准备工作打下基础。

四、教学资源1.教材：北师大版六年级下册数学教材；2.小黑板或白板、彩色粉笔或笔、教学PPT等。

五、教学评价本节课程采用形式多样的教学方式，注重理论和实际联系，充分发挥学生的主动性，培养学生的数学思维和方法，同时注意培养学生的创新意识，并确保学生能够正确、熟练地掌握本节课的知识和技能。

《比和比例整理与复习》教案设计楚江中心小学黄利飞教学目标：1、情感目标：在复习活动中让学生体验数学与生活实际的密切联系，培养学生的数学应用意识，激发学生成功学习数学和自信心和创新意识，渗透事物间是相互联系的辩证唯物主义观点。

2、能力目标：通过整理知识框架，提高学习的系统性，培养学生归纳、总结等自我复习能力，加强自主学习能力和综合运用数学知识解决实际生活问题的能力。

3、知识目标：使学生进一步掌握比和比例的意义、性质，能正确迅速地解比例、化简比和求比值。

教学重点：理解比和比例的意义、性质，掌握关于比和比例的一些实际运用和计算。

教学难点：能理清知识间的联系，建构起知识网络。

教学过程：一、创设情景，导入复习以名侦探柯南的情景，导入新课。

引出比与比例的复习。

（板书标题——比与比例的复习）二、展开活动，进入复习1、（1）教师提问：什么是比？学生举例，教师在黑板板书比的意义。

（2）教师提问：什么是比值？学生齐声回答。

（课件展示 比值 ）课件展示习题。

2、复习比和除法和分数的关系（1）由3：5=3÷5=53，引出a ：b=a ÷b=ba (强调b ≠0和比的后项不能为“0”)（2）填表比和除法﹑分数的联系课件展示表格3、复习比的基本性质（1）点名学生作答比的基本性质课件展示，黑板板书比的基本性质。

（2）比的基本性质的应用教师引导——化简比（3）习题讲解，加深学生理解①火眼金睛用比的基本性质判断下面各题。

4：15=（4x3）:（15÷3）=12 : 5 21 ：31 =（ 21x6）:（ 31 x6）= 3 :2 15米:10分米=（15÷5）:（10÷5）=3 : 2②化简下面各比35 : 15 4 : 0.8 1.5吨 : 300千克4、进入比值的复习①课件展示同一幅画面的放大与缩小图教师提问：你能分别写出这两幅图长于宽的比吗？学生回答，教师黑板板书两个比 20：15 40：30 继续提问：这两个比之间有什么关系？学生齐答：相等。

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

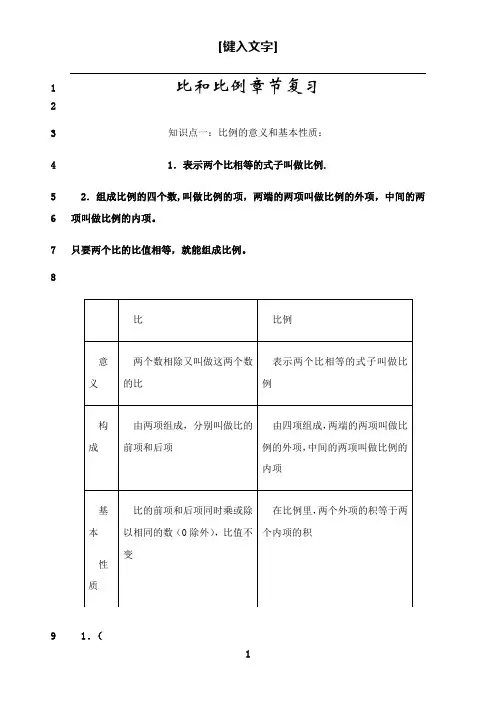
比和比例章节复习123知识点一：比例的意义和基本性质：41．表示两个比相等的式子叫做比例.52．组成比例的四个数,叫做比例的项，两端的两项叫做比例的外项，中间的两6项叫做比例的内项。

7只要两个比的比值相等，就能组成比例。

89）叫做比例。

102．（ 11）这叫做比例的12基本性质。

133．（ 14）叫做解比例。

154．两个比的（ ）相等，这两个比就相等。

16知识点二：正反比例的比较和应用 17正比例：两种相关联的量，一种量变化，另一种量也随着变化，且这两种量中18相对应的两个数的比值（或商）一定，这两种量就叫做成正比例的量，它们的关19系就叫正比例关系。

正比例关系用字母表示为：x y = k （一定）。

20反比例：两种相关联的量，一种量变化，另一种量也随着变化，且这两种量中21相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系就叫反比22例关系。

反比例关系用字母表示为：x ×y = k （一定）。

23正比例的图像是直线，反比例的图像是曲线。

24例题讲解： 25一、判断下列量是否是正反比例关系 261.如果工作时间一定，那么工作总量与工作效率成（ ）比例关系。

272.如果工作总量一定，那么工作时间与工作效率成（ ）比例关系。

283.汽车的耗油量一定，油箱中汽油的数量与行驶的路程成（ ）比例关系。

294.出售小麦的单价一定，出售小麦总量与总钱数成（ ）比例关系。

305.体操比赛的总人数一定，每排人数与排数成（ ）比例关系。

31例2、实际应用 321、一根电线，长70米，重15.4千克，现有这种电线940米，重多少千克？ 333435362、100千克小麦可磨出面粉85千克，照这样计算，6吨小麦可以磨出面粉多少37千克？ 383、同学们做操，每行站15人，正好站12行。

如果每行站9人，可以站多少行？ 39404142434、给一间房子铺地，如果用边长6分米的方砖，需要80块。

比和比例章节复习知识点一：比例的意义和基本性质： 1．表示两个比相等的式子叫做比例.2．组成比例的四个数,叫做比例的项，两端的两项叫做比例的外项，中间的两项叫做比例的内项。

只要两个比的比值相等，就能组成比例。

1．（ ）叫做比例。

2．（ ）这叫做比例的基本性质。

3．（ ）叫做解比例。

4．两个比的（ ）相等，这两个比就相等。

知识点二：正反比例的比较和应用正比例：两种相关联的量，一种量变化，另一种量也随着变化，且这两种量中相对应的两个数的比值（或商）一定，这两种量就叫做成正比例的量，它们的关系就叫正比例关系。

正比例关系用字母表示为：xy= k （一定）。

反比例：两种相关联的量，一种量变化，另一种量也随着变化，且这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系就叫反比例关系。

反比例关系用字母表示为：x ×y = k （一定）。

正比例的图像是直线，反比例的图像是曲线。

例题讲解：一、判断下列量是否是正反比例关系1.如果工作时间一定，那么工作总量与工作效率成（ ）比例关系。

2.如果工作总量一定，那么工作时间与工作效率成（ ）比例关系。

3.汽车的耗油量一定，油箱中汽油的数量与行驶的路程成（ ）比例关系。

4.出售小麦的单价一定，出售小麦总量与总钱数成（ ）比例关系。

5.体操比赛的总人数一定，每排人数与排数成（ ）比例关系。

例2、实际应用1、一根电线，长70米，重15.4千克，现有这种电线940米，重多少千克？2、100千克小麦可磨出面粉85千克，照这样计算，6吨小麦可以磨出面粉多少千克？3、同学们做操，每行站15人，正好站12行。

如果每行站9人，可以站多少行？4、给一间房子铺地，如果用边长6分米的方砖，需要80块。

如果改用边长8分米的方砖，需要多少块？知识点三、比例尺图上距离与实际距离的比，叫这幅图的比例尺。

实际距离图上距离比例尺1. 数字比例尺 如：1：3000 000 图上1厘米表示实际3000 000厘米。

[键入文字]比和比例章节复习知识点一：比例的意义和根本性质：1．表示两个比相等的式子叫做比例 .2．组成比例的四个数,叫做比例的项，两端的两项叫做比例的外项，中间的两项叫做比例的内项。

只要两个比的比值相等，就能组成比例。

比比例意义两个数相除又叫做这两个数的比表示两个比相等的式子叫做比例构成由两项组成，分别叫做比的前项和由四项组成，两端的两项叫做比例的外后项项，中间的两项叫做比例的内项根本比的前项和后项同时乘或除以相在比例里，两个外项的积等于两个内项性质同的数〔0除外〕，比值不变的积．〔〕叫做比例。

2．〔〕这叫做比例的基本性质。

3．〔4．两个比的〔〕叫做解比例。

〕相等，这两个比就相等。

知识点二：正反比例的比较和应用正比例：两种相关联的量，一种量变化，另一种量也随着变化，且这两种量中相对应的两个数的比值〔或商〕一定，这两种量就叫做成正比例的量，它们的关系就叫正比例关系。

正比例关系用字母表示为：=k〔一定〕。

x反比例：两种相关联的量，一种量变化，另一种量也随着变化，且这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系就叫反比例关系。

反比例关系用字母表示为：x×y=k〔一定〕。

正比例的图像是直线，反比例的图像是曲线。

例题讲解：一、判断以下量是否是正反比例关系1.如果工作时间一定，那么工作总量与工作效率成〔〕比例关系。

2.如果工作总量一定，那么工作时间与工作效率成〔〕比例关系。

3.汽车的耗油量一定，油箱中汽油的数量与行驶的路程成〔〕比例关系。

4.出售小麦的单价一定，出售小麦总量与总钱数成〔〕比例关系。

5.体操比赛的总人数一定，每排人数与排数成〔〕比例关系。

例2、实际应用[键入文字]1、一根电线，长70米，重千克，现有这种电线940米，重多少千克？2、100千克小麦可磨出面粉85千克，照这样计算，6吨小麦可以磨出面粉多少千克？3、同学们做操，每行站15人，正好站12行。

如果每行站9人，可以站多少行？4、给一间房子铺地，如果用边长6分米的方砖，需要80块。