第四节 轴向拉伸与压缩时的变形

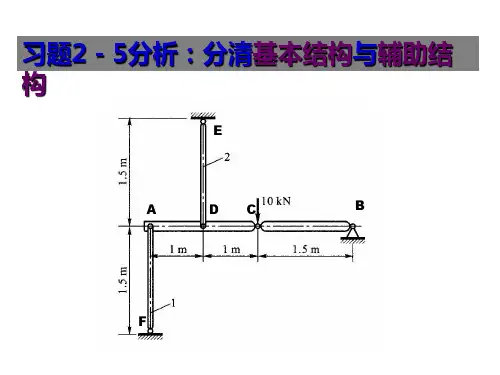
第五章 轴向拉伸与压缩一、轴向拉伸与压缩承受拉伸或压缩杆件的外力（或外力的合力）作用线与杆轴线重合，杆件沿杆轴线方向伸长或缩短，这种变形形式称为轴向拉伸或轴向压缩。

这种杆件称为拉压杆。

二、轴力及轴力图杆件在外力作用下将发生变形，同时杆件内部各部分之间产生相互作用力，此相互作用力称为内力。

对于轴向拉压杆，其内力作用线与轴线重合，此内力称为轴力。

轴力拉为正，压为负。

为了表现轴向拉压杆各横截面上轴力的变化情况，工程上常以轴力图表示杆件轴力沿杆长的变化。

三、横截面上的应力根据圣文南原理，在离杆端一定距离之外，横截面上各点的变形是均匀的，各点的应力也应是均匀的，并垂直于横截面，此即为正应力。

设杆的横截面面积为Ａ，则有AF N =σ 工程计算中设定拉应力为正，压应力为负。

四、强度条件工程中为各种材料规定了设计构件时工作应力的最高限度，称为许用应力，用［σ］表示。

轴向拉伸（压缩）强度条件为[]σσ≤=AF N用强度条件可解决工程中三个方面的强度计算问题，即：（1）强度校核；（2）设计截面；（3）确定许可载荷。

五、斜截面上的应力与横截面成θ角的任一斜截面上，通常有正应力和切应力存在，它们与横截面正应力σ的关系为：⎪⎪⎩⎪⎪⎨⎧=+=θστθσσθθ2sin 2)2cos 1(2 由上式可知，当θ＝０°时，正应力最大，即横截面上的正应力是所有截面上正应力中的最大值。

当θ＝±４５°时，切应力达到极值。

六、拉压变形与胡克定律等值杆受轴向拉力Ｆ作用，杆的原长为l ，横截面积为Ａ，变形后杆长由l 变为l ＋△l ，则杆的轴向伸长为EAFl l =∆ 用内力表示为EAl F l N =∆ 上式为杆件拉伸（压缩）时的胡克定律。

式中的Ｅ称为材料的拉伸（压缩）弹性摸量，ＥＡ称为抗拉（压）刚度。

用应力与应变表示的胡克定律为σ＝Ｅε在弹性范围内，杆件的横向应变ε‘和轴向应变ε有如下的关系：μεε-='式中的μ称为泊松比。

第四章杆件的变形计算杆件在载荷作用下都将发生变形，过大的变形将影响杆件的正常使用，必须加以限制，而有时又希望杆件能有较大的变形，以起缓冲作用，如弹簧等，因此必须计算杆件的变形。

本章具体讨论了拉伸（压缩）、扭转、弯曲三种情况的杆件变形计算。

第一节拉（压）杆的轴向变形直杆在沿其轴线的外力作用下，纵向发生伸长或缩短变形，而其横向相应变细或变粗，如图4-1所示。

设杆原长l，宽b，在力F作用下产生变形，变形后长l1，宽b1。

则杆件在轴线方向的伸长为纵向应变为根据虎克定律和拉（压）杆横截面正应力公式，可以得到（4-1）上式表明，杆的轴向变形值与轴力F N及杆长l成正比，与材料的杨氏模量及杆的横截面面积成反比。

因此EA称为拉（压）杆的抗拉（压）刚度，EA值越大，杆件刚度越大，在一定外力作用下单位长度变形量就越小。

另一方面，横向变形,横向应变。

通过试验发现，当材料在弹性范围内时，拉（压）杆的纵向应变与横向应变之间存在如下比例关系：(4-2a)或=-（4-2b）式中比例常数称为泊松比。

弹性模量E、泊松比及切变模量G均是材料的弹性常数，可由实验测得。

对于各向同性材料，可以证明这三个弹性常数之间存在下列关系：（4-3）材料的值小于0.5，表4-1列出几种常见金属材料的E和的值。

例4-1 阶梯形直杆受轴力如图4-2，已知该杆AB段横截面面积A1=800mm2 , 段横截面面积A2=240mm2，杆件材料的弹性模量为E=200GPa。

试求该杆总伸长量。

解（1）求AB、BC段轴力F NAB=40kN（拉），F NBC=-20kN（压）（2）求AB、BC段伸长量AB段BC段由以上计算可以看出，AB段是伸长，而BC段是缩短。

（3）AC杆总伸长AC杆计算结果为负，说明AC杆是缩短而不是伸长。

例4-2 图示桁架，钢杆AC横截面面积A1=960mm ，弹性模量E1=200GPa。

木杆BC横截面，杨氏模量E2=10GPa 。

求铰节点C的位移。

轴向拉伸和压缩时的变形公式概述及解释说明1. 引言1.1 概述本文主要介绍轴向拉伸和压缩下物体的变形公式及其解释说明。

在工程领域中，了解材料在不同应力条件下的变形规律对设计和使用具有重要意义。

轴向拉伸和压缩是常见的应力状态，通过研究这两种情况下的变形公式，可以帮助工程师更好地理解和预测物体的变形行为。

1.2 文章结构本文共分为四个部分进行阐述。

引言部分主要对文章进行总览和概述。

接下来,“2. 轴向拉伸时的变形公式”将详细介绍轴向拉伸过程中物体的变形规律，并包括弹性阶段和塑性阶段的应变公式以及变形模量的定义与计算方法。

“3. 轴向压缩时的变形公式”将探讨轴向压缩情况下物体的应变规律，并包括弹性阶段和塑性阶段的应变公式，以及计算压缩强度和稳定塑性流动区域大小的方法。

“4 结论”将总结轴向拉伸和压缩时的变形规律与公式，并展望其在工程实践中的意义和应用前景。

1.3 目的本文的目的是系统地介绍轴向拉伸和压缩时物体变形的公式及其解释说明。

通过深入探讨材料在不同应力状态下的变形规律，旨在增强读者对工程材料性能的理解，并提供有关设计和应用方面的参考。

此外，文章还将揭示轴向拉伸和压缩时变形公式的工程实践意义，为相关领域的研究者和从业人员提供参考。

2. 轴向拉伸时的变形公式2.1 弹性阶段的应变公式：在轴向拉伸时，当物体处于弹性阶段时，变形可以通过应变来描述。

应变是指物体在受力作用下产生的长度或形状改变与初始长度或形状之比。

弹性阶段的应变公式可以用胡克定律表示，即应力和应变成正比。

应变公式可以表示为：ε= σ/ E其中，ε表示轴向拉伸时的应变，σ表示受试样所受到的轴向拉伸力，E表示材料的弹性模量。

2.2 塑性阶段的应变公式：当材料超过其弹性极限，进入塑性阶段时，其应变特性就会发生改变。

塑性阶段的应变公式可以通过流动理论进行描述。

在塑性阶段中，通常采用等效塑性应变概念。

等效塑性应变是根据材料的真实应力-真实塑性曲线（即压缩-延展曲线）求得，在一定条件下模拟材料的本构关系。

第4章轴向拉伸与压缩4.1 轴向拉伸与压缩的概念在建筑物和机械等工程结构中，经常使用受拉伸或压缩的构件。

例如图4.1所示液压传动中的活塞杆，工作时以拉伸和压缩变形为主。

图4.2所示拧紧的螺栓，螺栓杆以拉伸变形为主。

图4.1 图4.2图4.3所示拔桩机在工作时，油缸顶起吊臂将桩从地下拔起，油缸杆受压缩变形，桩在拔起时受拉伸变形，钢丝绳受拉伸变形。

图4.4所示桥墩承受桥面传来的载荷，以压缩变形为主。

图4.3 图4.4图4.5所示钢木组合桁架中的钢拉杆，以拉伸变形为主。

图4.6所示厂房用的混凝土立柱以压缩变形为主。

图4.5 图4.6 在工程中以拉伸或压缩为主要变形的构件，称为拉、压杆，若杆件所承受的外力或外力合力作用线与杆轴线重合，称为轴向拉伸或轴向压缩。

4.2 轴向拉(压)杆的内力与轴力图4.2.1 拉压杆的内力在轴向外力F 作用下的等直杆，如图4.7（a ）所示，利用截面法，可以确定n m -横截面上的唯一内力分量为轴力N F ，其作用线垂直于横截面并通过形心，如图4.7（b ）所示。

图4.7利用平衡方程 0=∑x F得 F F =N通常规定：轴力N F 使杆件受拉为正，受压为负。

4.2.2 轴力图为了表明轴力沿杆轴线变化的情况，用平行于轴线的坐标表示横截面的位置，垂直于杆轴线的坐标表示横截面上轴力的数值，以此表示轴力与横截面位置关系的几何图形，称为轴力图。

作轴力图时应注意以下几点：1、轴力图的位置应和杆件的位置相对应。

轴力的大小，按比例画在坐标上，并在图上标出代表点数值。

2、习惯上将正值（拉力）的轴力图画在坐标的正向；负值（压力）的轴力图画在坐标的负向。

例题4.1 一等直杆及受力情况如图（a ）所示，试作杆的轴力图。

如何调整外力，使杆上轴力分布得比较合理。

例题4.1图解：（1）、求AB 段轴力用假设截面在1–1处截开，设轴力F N 为拉力，其指向背离横截面，由平衡方程得kN 5N1 F （图b ）（2）、同理，求BC 段轴力kN 15kN 10kN 5N2=+=F （图c ）（3）、求CD 段轴力，为简化计算，取右段为分离体kN 30N3=F （图d ）（4）、按作轴力图的规则，作出轴力图，如图（e ）所示。

轴向拉伸与压缩的名词解释引言：轴向拉伸与压缩是物理学领域中常见的概念，用于描述物体在力的作用下的变形情况。

本文将对轴向拉伸与压缩进行详细的解释与探讨。

一、轴向拉伸轴向拉伸是指物体在受到拉力作用下沿着其长度方向发生的变形现象。

当外力作用于物体的两端，并朝外拉伸时，物体会在轴向上发生拉伸。

拉伸的大小可以通过物体的伸长率来衡量，伸长率定义为单位长度的伸长与初始长度之比。

轴向拉伸现象广泛应用于工程领域，例如建筑中的钢筋，拉伸试验中的拉力传感器等。

钢筋在混凝土中起到增强材料的作用，能够抵抗建筑物的拉力。

而拉力传感器则是一种能够测量外力大小的传感器，利用了材料的拉伸特性。

二、轴向压缩轴向压缩是指物体在受到压力作用下沿着其长度方向发生的变形现象。

当外力作用于物体的两端，并朝内压缩时，物体会在轴向上发生压缩。

压缩的大小可以通过物体的压缩率来衡量，压缩率定义为单位长度的压缩与初始长度之比。

轴向压缩现象同样广泛应用于工程领域。

例如，桥梁中的墩柱、压缩试验中的压力传感器等。

墩柱是承受桥梁重力和交通荷载的重要结构部件，压缩试验中的压力传感器则是能够测量外力大小的传感器，利用了材料的压缩特性。

三、轴向拉伸与压缩的应用轴向拉伸与压缩的应用十分丰富，不仅在工程领域中有广泛应用，在其他领域中也有其独特的应用价值。

1. 材料科学：轴向拉伸与压缩是材料性能研究的重要手段。

通过对材料在拉伸和压缩条件下的变形进行测试，可以获得材料的各种力学性能参数，例如抗拉强度、抗压强度等。

这对材料的设计和应用具有重要的指导意义。

2. 生物医学：轴向拉伸与压缩在生物医学研究中具有重要的作用。

例如，在骨骼生物力学研究中，可以通过对骨骼的拉伸和压缩测试，了解骨骼力学特性并分析疾病的发生机制。

3. 电子工程：轴向拉伸与压缩的特性也可以应用于电子工程领域。

例如，电子产品中常使用弹性材料来保护内部电路。

这些材料可以在外力作用下发生轴向拉伸或压缩，起到减缓冲击力的作用。