第十二章 试验设计

⽣物统计考试计算题（第五,六,七,⼗⼆章复习重点）第五章假设检验（t 检验）1.某品种鸡4周龄标准体重是0.625kg,现饲养该品种⼀批，4周龄随机抽取50只，测得平均体重0.584kg,标准差0.135kg , 试分析这批鸡体重与标准体重有⽆显著差异。

各处理差=0.625-0.584=0.041引起原因可能是处理效应或试验误差 t=2.147 , P(H0)=0.037表⽰：u=0.625的概率是0.037，相反u ≠0.625的概率是0.963。

2.1）、什么条件下可能犯Ⅰ型错误，其与显著⽔平⼜有何关系。

2）、什么条件下可能犯Ⅱ型错误。

3）、统计推断的结论是否绝对正确，为什么。

3.某品种鸡的平均蛋重30克，现随机抽取10枚蛋重量如下：（单位：克） 30 、 32 、 31 、 30、 31 31、 31 、 31 、 30 、32试分析样本所在总体均数与蛋重30克有⽆显著差异。

解：1、提出⽆效假设与备择假设 H0： = 30 ； HA ： ≠ 302、计算 t 值经计算得： x =30.90，S =0.7423.0S =x 所以xS ux t -==(30.9-30)0.23= 3.91df=n-1=10-1=93、查临界t 值，作出统计推断因为 t0.05(9)= 2.262，t0.01(9)=3.25 ，否定H0 ： =30，接受HA ： ≠30，表⽰这批蛋重与30克有极显著差异。

4.按规定⾁鸡平均体重≥3kg ⽅可出售，现从鸡群中随机抽取16只，平均体重为2.8公⽄，标准差为0.2公⽄，问该批鸡可否出售。

解：1、提出⽆效假设与备择假设 H0： = 3，HA ：＜32、计算 t 值经计算得：x =2.8，S =0.205.0S =xxS ux t -== (3-2.8)/0.05 = 4 df=n-1=16-1=153.查临界t 值，作出统计推断因为 t0.05*2(15)= 1.753，t0.01*2(15)=2.49 ，否定H0 ：u =3，接受HA ：u ＜3，表⽰这批鸡还不能出售。

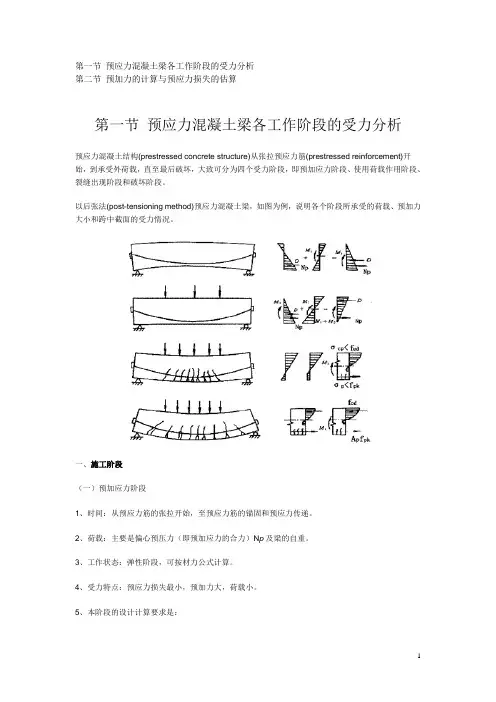
第一节预应力混凝土梁各工作阶段的受力分析第二节预加力的计算与预应力损失的估算第一节预应力混凝土梁各工作阶段的受力分析预应力混凝土结构(prestressed concrete structure)从张拉预应力筋(prestressed reinforcement)开始，到承受外荷载，直至最后破坏，大致可分为四个受力阶段，即预加应力阶段、使用荷载作用阶段、裂缝出现阶段和破坏阶段。

以后张法(post-tensioning method)预应力混凝土梁，如图为例，说明各个阶段所承受的荷载、预加力大小和跨中截面的受力情况。

一、施工阶段（一）预加应力阶段1、时间：从预应力筋的张拉开始，至预应力筋的锚固和预应力传递。

2、荷载：主要是偏心预压力（即预加应力的合力）N p及梁的自重。

3、工作状态：弹性阶段，可按材力公式计算。

4、受力特点：预应力损失最小，预加力大，荷载小。

5、本阶段的设计计算要求是：①控制梁的上、下缘混凝土的最大拉应力和压应力，及梁腹的主应力，不应超出《公桥规》的规定；②控制钢筋的最大张拉应力；③保证锚具下混凝土局部承压的容许承载能力，使其大于实际承载的压力，并有足够的安全度，以保证梁体不出现水平纵向裂缝。

6、有效预应力的概念：通常把扣除应力损失后钢筋中实际存余的应力称为有效预应力（effective Prestress）。

（二）运输、安装阶段此阶段混凝土梁所承受的荷载，仍是预加力和梁的自身恒载。

但由于引起预应力损失的因素相继增加，使要比预加应力阶段小；同时梁的自身恒载应根据《公桥规》的规定计入1.20或0.85的动力系数。

构件在运输中的支点或安装时的吊点位置常与正常支承点不同，故应按梁起吊时自身恒载作用下的计算图式进行验算，特别需注意验算构件支点或吊点处上缘混凝土的拉应力。

二、使用阶段1、时间：该阶段是指桥梁建成通车后整个使用阶段。

2、荷载：梁自重（称为Ⅰ期恒载），偏心预加力N p，车辆及人群等活载，和桥面铺装、人行道板、栏杆等后加桥梁恒载（称为Ⅱ期恒载）。

第二节熔化与凝固【教学目标】一、知识与技能1。

理解气态、固态和液态是物质存在的三种形态.2.知道物质的固态和液态之间是可以相互转化的。

3.理解熔化的含义，了解晶体和非晶体的区别。

4.理解凝固的含义．5．知道熔化曲线和凝固曲线的物理含义。

二、过程与方法１。

通过探究固体熔化时温度变化的规律,感知发生物态变化的条件.2．了解有无固定的熔化温度是区别晶体和非晶体的一种方法。

3。

通过探究活动,使学生了解图像是一种比较直观的表示物理量变化的方法.三、情感、态度与价值观通过教学活动,激发学生对自然现象的关心,产生乐于探索自然现象的情感。

【教学重点】通过实验探究熔化、凝固的规律。

【教学难点】1.对熔化的理解.2．对凝固的理解及晶体与非晶体概念和性质的理解。

3。

晶体、非晶体熔化与凝固图像的区别.【教具准备】学生实验，六人一组。

每组配备熔化实验仪器：酒精灯、铁架台、石棉网、温度计两支、试管两支、石蜡、冰、火柴、坐标纸、多媒体课件等。

【教学课时】2课时【巩固复习】教师引导学生复习上一节所学内容,并讲解学生所做的课后作业（教师可针对性地挑选部分难题讲解),加强学生对知识的巩固。

【新课引入】师教师演示蜡烛“流泪"小实验,引导学生观察思考这里发生的物态变化是什么。

生:熔化。

师教师播放炼钢厂炼钢的相关视频,引导学生观察思考这里发生的物态变化是什么.生：熔化、凝固.师同学们真棒！下面，我们就来学习第二节“熔化与凝固”.【预习指导】阅读课本P9—14文字内容和插图，把基本概念、规定、规律,以及晶体、非晶体的不同点等用红色笔做上记号，并完成对应练习册中“课前预习”部分,然后，各小组内部交流讨论,提出预习疑问,组长做好记录，准备展示.【交流展示】１.各小组代表举手发言,报告“课前预习”答案，教师评价订正。

２。

学生质疑,教师指导释疑。

【拓展探究】熔化一、学生小组内部讨论交流，回答下列问题。

师举例说明什么是熔化?什么是凝固？生:冰冻的黄河解冻；固态的铁、锡等金属丝在高温下变成了液态等是熔化,我们把物质从固态变为液态的过程,称为熔化。

第十二章实验设计12.1一项关于在干旱地区生长的一种杨树（Populus euphratica），在土壤中的水分逐渐丧失后，其基因表达、蛋白谱、生态生理学及生长性能等方面产生可逆性改变的研究。

作者在本实验的5个时间点上（H5为对照），用qPCR方法度量了该杨树叶子中的三个基因的转录丰度比[83]，表中给出的为阵列数据：GenBank ID 基因H1H2H3H4H5AJ 780 423 半胱氨酸蛋白酶0.7 1.0 2.3 13.1 1.9AJ 780 698 环核苷酸和钙调节的离子通道 1.5 1.2 3.0 4.3 1.5AJ 777 362 核糖体蛋白 1.1 1.1 1.0 0.9 1.2借用上述数据，以三个基因作为三个区组，计算在5个时间点上转录丰度比差异是否显著？答：随机化完全区组实验设计方差分析的程序，类似于两因素交叉分组实验设计。

以下是本题的程序和结果：options linesize=76 nodate;data poplar;do block=1 to 3;do time=1 to 5;input trans @@;output;end;end;cards;0.7 1.0 2.3 13.1 1.91.5 1.2 3.0 4.3 1.51.1 1.1 1.0 0.9 1.2;proc anova;class block time;model trans=block time;run;The SAS SystemThe ANOVA ProcedureClass Level InformationClass Levels Valuesblock 3 1 2 3time 5 1 2 3 4 5Number of observations 15The SAS SystemThe ANOVA ProcedureDependent Variable: transSum ofSource DF Squares Mean Square F Value Pr > F Model 6 72.5560000 12.0926667 1.53 0.2809Error 8 63.1013333 7.8876667Corrected Total 14 135.6573333R-Square Coeff Var Root MSE trans Mean0.534848 117.6745 2.808499 2.386667Source DF Anova SS Mean Square F Value Pr > F block 2 18.82533333 9.41266667 1.19 0.3519 time 4 53.73066667 13.43266667 1.70 0.2416从上表中的结果可以看出，如果按随机化完全区组设计进行分析，不同时间点之间的差异不显著。

第十二章全等三角形1.理解和掌握全等三角形的概念,明确对应边、对应角、对应顶点等相关概念.2.掌握两个三角形全等,对应边相等、对应角相等的性质.3.探索并掌握两个三角形全等的条件,并能根据“SSS”“SAS”“ASA”“AAS”“HL”判定两个三角形全等.4.能够画已知角的平分线并掌握角平分线的性质定理和判定定理.1.通过观察、试验、归纳、类比、推理获得数学猜想,体验数学活动充满着探索性和创造性,感受证明的必要性、证明过程的严谨性以及结论的确定性.2.在教学中,注重所学内容与现实生活的联系;注重学生经历观察、操作、推理、想象等探索过程.1.让学生通过动手操作,感受知识的形成过程,树立认真学习的态度,激发学生的学习热情.2.利用小组合作的学习方法,让学生多进行交流,多种感官参与教学,使学生主动探索、发现规律、归纳概括、形成能力,养成学数学、爱数学的情感.中学阶段重点研究的两个平面图形间的关系是全等和相似,本章将以三角形为例研究全等.全等三角形研究的问题和研究方法将为后面学习相似提供思路,而且全等是一种特殊的相似,全等三角形的内容是学生学习相似三角形的重要基础.本章还将借助全等三角形进一步培养学生的推理论证能力,主要包括用分析法分析条件与结论的关系,用综合法书写证明格式,以及掌握证明几何命题的一般过程.由于利用全等三角形可以证明线段、角等基本几何元素相等,所以本章的内容也是学习等腰三角形、四边形、圆等内容的基础.本章分为三节,主要介绍了全等三角形的概念、性质、判定方法,以及如何利用三角形全等进行证明.第12.1节首先介绍了现实世界中的全等现象,然后从“重合”的角度引入了全等形的概念,在此基础上给出了全等三角形的概念,接着由全等三角形的概念导出了全等三角形的性质.第12.2节由图形的性质与判定在命题陈述上的互逆关系出发,引出判定两个三角形全等的方法.第12.3节首先由平分角的仪器的工作原理引出了作一个角的平分线的尺规作图,然后探究并证明了角的平分线的性质,同时总结了证明一个几何命题的一般步骤,最后给出了角的平分线的性质定理的逆定理.本章将重点研究三角形全等的判定方法,并在其中渗透了研究几何图形的基本方法.本章既有直接利用三角形全等的判定方法证明两个三角形全等的问题,又有通过证明两个三角形全等推出线段相等或角相等的问题,在问题的设计中还融入了平行线的性质与判定、三角形中边和角的等量关系、折纸情境等内容,推理论证的难度比《三角形》一章增大了.【重点】1.全等三角形的性质及各种判定三角形全等的方法.2.角平分线的性质及判定.3.证明的基本过程.【难点】1.根据不同条件合理选用三角形全等的判定方法,特别是对“SSA”不能判定三角形全等的认识.2.角平分线的性质和判定的正确运用.3.用综合法证明的格式.1.用研究几何图形的基本思想和方法贯穿本章的教学.学生在前面的几何学习中研究了相交线与平行线、三角形等几何图形,对于研究几何图形的基本问题、思路和方法形成了一定的认识,本章在教学中要充分利用学生已有的研究几何图形的思想方法,用几何思想贯穿全章的教学.2.让学生充分经历探究过程.本章在编排判定三角形全等的内容时构建了一个完整的探究活动,包括探究的目标、探究的思路和分阶段的探究活动.教学中可以让学生充分经历这个探究过程,在明确探究目标、形成探究思路的前提下,按计划逐步探索两个三角形全等的条件.本章在编排中将画图与探究三角形全等的条件结合起来, 既有用尺规画一个三角形与已知三角形全等,又有用技术手段根据已知数据画三角形.教学中要充分利用探索画图方法的过程对形成结论的价值,让学生自主探索画图的步骤、创设多种画法、解释作图依据等,在活动中发现结论.3.重视对学生推理论证能力的培养.本章是初中阶段培养逻辑推理能力的重要章节,主要包括证明两个三角形全等,通过证明三角形全等,进而证得两条线段或两个角相等.教学中要在学生已有推理论证经验的基础上,利用三角形全等的证明,进一步培养学生推理论证的能力.按照整套教科书对推理能力培养的循序渐进的目标,本章的教学重点是引导学生分析条件与结论的关系,书写严谨的证明格式,从具体问题的证明中总结出证明的一般步骤.12.1全等三角形1课时12.2三角形全等的判定4课时12.3角的平分线的性质1课时单元复习1课时12.1全等三角形1.掌握好全等形及全等三角形的定义.2.理解对应顶点、对应边、对应角的含义.3.掌握全等三角形的性质.1.教学时结合实际图片或学生自己动手制作的图片,使学生更加容易接受本节的知识,也能从中体会到数学的乐趣及数学与生活实际的联系.2.通过对一个图形的平移、翻折、旋转等动态变换,使学生的思维更具动态,形成空间观念,对以后的图形观察与总结具有更好的指引作用.1.在全等形的引入中,通过一些实际生活的图片,让学生感受到数学来源于生活实际,又反作用于生活实际.2.在学习中,同学之间以及小组之间相互研讨,可促进学生的团队意识,以及认识合作的价值.【重点】掌握好全等三角形的定义及利用全等三角形的性质解决问题.【难点】全等三角形性质的应用.【教师准备】全等的三角形纸板.【学生准备】剪刀、三角形纸板.导入一:(老师手拿两个全等的三角形纸板,可先分开操作,然后把两个三角形进行重合操作,目的是让学生看出这两个三角形是能够完全重合在一起的) 【师】同学们,你能发现这两个三角形有什么关系吗?【生】这两个三角形是完全重合的.【师】这就是我们今天要学习的全等形中的一种,全等三角形.(同时教师手写板书)[设计意图]本节的内容,对于学生来说还是比较容易接受的,所以此设计比较简捷,单刀直入,可以节省时间,直入主题.导入二:【师】同学们,这节课我们先做个游戏,把你们准备好的剪刀与三角形纸板拿出来,先取一张纸,将准备好的三角形纸板按在纸上,画下图形,照图形裁下来,观察一下,有什么特点?同桌之间互相配合完成,再一起讨论得到的三角形与原三角形之间的关系.[设计意图]同桌之间通过互相帮助,动手探索,既能增强他们的合作意识、团队精神,又能在动手操作中感受到数学的乐趣,增强对全等三角形的认知与理解.导入三:(老师拿出一块硬纸板)同学们请看,每组的两个图形有什么特点?它们的形状、大小一样吗?它们能互相重合吗?[设计意图]这两个问题和实际生活的联系比较密切,引起了学生认知的需要,激发了学生的求知欲,使之在思维情境中进入最佳的学习状态.这就为学生认识和探索全等三角形的性质做了铺垫.一、全等三角形的相关概念1.全等形的概念思路一【师生活动一】多找一些学生举例子.(此过程中,有些学生举的例子是不正确的,如有的学生可能会说“双胞胎”,可先让学生说说此例子是否正确,让学生们一起讨论,然后老师给出正确的指引及错误的原因,对学生的不同回答,只要合理,就给予认可)[设计意图]帮助学生准确地理解定义,以及感受数学知识的严谨性.【师生活动二】(1)上面同学们举的这些例子,有什么共同的特征?(2)有人用“全等形”一词描述上面的图形,你认为这个词是什么含义?同学们畅所欲言,最后老师给出全等形及全等三角形的定义,为了加深理解,可通过列举反例强调定义的条件.全等形的定义:能够完全重合的两个图形叫做全等形.全等三角形的定义:能够完全重合的两个三角形叫做全等三角形.思路二【学生活动一】把一块三角形样板按在纸板上,画下图形,照图形裁下来.【问题思考】裁下来的纸板和样板的形状、大小完全一样吗?把样板和裁得的纸板放在一起能够完全重合吗?用同一张底片冲洗出来的两张照片上的图形,放在一起也能够完全重合吗?【学生回答后总结】能够完全重合的两个图形叫做全等形.[设计意图]从学生熟悉的图形和例子引出全等形的概念,可以排除学生对几何的畏惧心理,增强他们的自信心,在教学过程中要强调“重合”的重要性,使全等形的概念的引入显得更加自然.【学生活动二】观察黑板上的两个三角形ΔDEF和ΔABC.【思考】如果把ΔDEF放到ΔABC上,两个三角形可以重合吗?可以重合的三角形称为什么?【生答】全等三角形.[设计意图]通过这个活动及时巩固全等形的概念,同时也为后面的内容做铺垫,起承上启下的作用.[拓展延伸]两个三角形全等指的是两个三角形的形状和大小完全相同,和位置无关.2.全等三角形的相关定义【师生活动一】老师演示以下三种情况:(1)将ΔABC沿直线BC平移得到ΔDEF;(2)将ΔABC沿BC翻折180°得到ΔDBC;(3)将ΔABC绕点A旋转180°得到ΔAED.【议一议】各图中的两个三角形全等吗?它们能完全重合,我们就说它们是全等三角形,其中能重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.如上图中的甲,ΔABC与ΔDEF全等,我们就记作ΔABC≌ΔDEF,符号“≌”读作“全等于”,当两个三角形全等时,我们就用它来表示.其中点A与点D,点B与点E,点C与点F是对应顶点;AB与DE,BC与EF,AC与DF是对应边;∠A和∠D,∠B和∠E,∠C和∠F是对应角.同学们,能不能对上述的图乙,图丙,分别说出它们的记法、读法,以及其中的对应顶点、对应边、对应角.当学生回答两个三角形全等的书写时,教师注意强调书写时对应顶点字母写在对应的位置上.【师生活动二】【师】由上述的演示可以看出,一个图形经过平移、翻折、旋转后,位置变化了,但形状、大小都没有改变,所以平移、翻折、旋转前后的图形全等,这也是我们通过运动的方法寻求全等的一种策略.在上述三种变换中,怎么能快速地找到对应顶点、对应边、对应角呢?请同学们讨论.[设计意图]学生进行讨论,各抒己见,此过程中学生说的不一定对,在互相的讨论、交流中,学生慢慢地纠正自己的错误,接受别人的好的方法,这样能更加深入地了解与掌握找全等三角形的对应点、对应边、对应角的方法.【师最后总结】在全等三角形中,找出对应角和对应边,关键是先找出对应顶点,然后按对应顶点的字母顺序记两个三角形全等,再按顺序写出对应边和对应角.全等三角形的面积一定相等,但是面积相等的两个三角形不一定是全等三角形.[知识拓展]找对应元素的常用方法有两种:(一)从运动角度看1.翻转法:找到中心线,沿中心线翻折后能相互重合,从而发现对应元素.2.旋转法:三角形绕某一点旋转一定角度后能与另一三角形重合,从而发现对应元素.3.平移法:沿某一方向平移使两三角形重合来找对应元素.(二)根据元素位置来推理1.全等三角形对应角所对的边是对应边;两个对应角所夹的边是对应边.2.全等三角形对应边所对的角是对应角;两条对应边所夹的角是对应角.3.公共边一定是对应边,公共角一定是对应角,对顶角一定是对应角.4.全等三角形中一对最短的边(或最小的角)是对应边(或对应角).二、全等三角形的性质学生们纷纷发言,在此过程中,老师引导学生从全等三角形可以完全重合出发找等量关系,得到全等三角形的性质:全等三角形的对应边相等;全等三角形的对应角相等.[知识拓展](1)全等三角形的对应边上的高、中线以及对应角的平分线相等;(2)全等三角形的周长相等,面积相等;(3)平移、翻折、旋转前后的图形全等.三、例题讲解如图所示,ΔOCA≌ΔOBD,C和B,A和D是对应顶点.(1)ΔOCA≌ΔOBD说明这两个三角形可以重合,那么通过怎样的变换可以使这两个三角形重合?(2)说出这两个三角形中相等的边和角.解:(1)将ΔOCA翻折可以使ΔOCA与ΔOBD重合.(2)∠C=∠B,∠A=∠D,∠AOC=∠DOB;AC=DB,OA=OD,OC=OB.如图所示,已知ΔABE≌ΔACD,∠ADE=∠AED,∠B=∠C,指出其他的对应边和对应角.〔解析〕对应边和对应角只能从两个三角形中找,所以需将ΔABE和ΔACD从复杂的图形中分离出来.根据元素位置来找,有相等元素,它们就是对应元素,再依据已知的对应元素找出其余的对应元素.解:对应角为∠BAE和∠CAD.对应边为AB与AC,AE与AD,BE与CD.1.能够完全重合的图形叫做全等形.能够完全重合的三角形叫做全等三角形.重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.全等三角形的对应边相等,对应角相等.2.找全等三角形对应元素的方法,注意挖掘图形中隐含的条件,如公共元素、对顶角等.3.在运用全等三角形的定义和性质时应注意规范书写格式.1.如图所示,ΔABC≌ΔDEF,则此图中相等的线段有()A.1对B.2对C.3对D.4对解析:因为ΔABC≌ΔDEF,所以AB=DE,AC=DF,BC=EF,因为BC=EF,即BE+EC=CF+EC,所以BE=CF,即有4对相等的线段.故选D.2.如图所示,ΔACB≌ΔA'CB',∠A'CB=30°,∠ACB'=110°,则∠ACA'的度数是()A.20°B.30°C.35°D.40°解析:∵ΔACB≌ΔA'CB',∴∠ACB=∠A'CB',∴∠ACB-∠A'CB=∠A'CB'-∠A'CB,即∠ACA'=∠BCB',∵∠A'CB=30°,∠ACB'=110°,∴∠ACA'=1(110°-30°)=40°.故选D.23.如图所示,找出由七巧板拼成的图案中的全等三角形.解:三角形1和三角形2,三角形6和三角形7.4.如图所示,已知ΔABC≌ΔADE,试找出对应边、对应角.解析:方法1:可以发现∠A是公共角,在两个三角形中∠A的对边分别是BC和DE,所以BC和DE是一组对应边.而AB与AE显然不重合,所以AB与AD是一组对应边,剩下的AC与AE自然是一组对应边了.再根据对应边所对的角是对应角可得∠B与∠D是对应角,∠ACB与∠AED是对应角.所以对应边为AB与AD,AC与AE,BC与DE.对应角为∠A与∠A,∠B与∠D,∠ACB与∠AED.方法2:沿A与BC和DE的交点O的连线将ΔABC翻折180°后,它正好和ΔADE重合,这时就可以找到对应边为AB与AD,AC与AE,BC与DE.对应角为∠A与∠A,∠B与∠D,∠ACB与∠AED.解:对应边为AB与AD,AC与AE,BC与DE.对应角为∠A与∠A,∠B与∠D,∠ACB与∠AED.12.1全等三角形一、全等三角形的相关概念二、全等三角形的性质例1例2一、教材作业【必做题】教材第32页练习第1,2题.【选做题】教材第33页习题12.1第3,4,5题.二、课后作业【基础巩固】1.下列各组图形中是全等图形的是()2.下列各组图形中,是全等形的是()A.对应钝角相等的两个等腰三角形B.两个含60°角的直角三角形C.边长为3和5的两个等腰三角形D.腰对应相等的两个直角三角形3.如图所示,ΔABC≌ΔBAD,点A和点B,点C和点D是对应顶点,如果AB=6cm,BD=5 cm,AD=4 cm,那么AC的长是()A.6 cmB.5 cmC.4 cmD.无法确定4.如图所示,RtΔABC≌RtΔDEF,则∠D的度数为()A.30°B.45°C.60°D.90°【能力提升】5.如图所示,四边形ABCD的对角线AC,BD相交于点O,ΔABC≌ΔBAD.求证:(1)OA=OB;(2)∠OCD=∠ODC.6.如图所示,ΔABC≌ΔAEC,B和E是对应顶点,∠B=30°,∠ACB=85°,求ΔAEC各内角的度数.【拓展探究】7.如图所示,已知ΔABD≌ΔACE,且点E在BD上,CE交AB于点F,若∠CAB=20°,求∠DEF的度数.【答案与解析】1.B(解析:根据全等图形的定义可得.)2.D3.B(解析:∵ΔABC≌ΔBAD,点A与点B,点C与点D是对应顶点,∴AC=BD,又∵BD=5 cm(已知),∴AC=5 cm.故选B.)4.A(解析:∵RtΔABC≌RtΔDEF,∴∠D=∠A.∵在RtΔABC中,∠A+∠B=90°,且∠B=60°,∴∠A=30°,∴∠D=30°.故选A.)5.证明:(1)∵ΔABC≌ΔBAD,∴∠CAB=∠DBA,∴OA=OB. (2)∵ΔABC≌ΔBAD,∴AC=BD,又∵OA=OB,∴AC-OA=BD-OB,即OC=OD,∴∠OCD=∠ODC.6.解:∵ΔABC≌ΔAEC,∴∠ACE=∠ACB,∠EAC=∠BAC,∠E=∠B,又∵∠B=30°,∠ACB=85°,∴∠E=30°,∠ACE=85°,∴∠EAC=65°.7.解析:根据全等三角形的性质求出∠C=∠B,再根据三角形内角和定理和对顶角相等求出∠BEF=∠CAB=20°,代入∠DEF=180°-∠BEF即可求出∠DEF.解:∵ΔABD≌ΔACE,∴∠C=∠B,∵∠BFE=∠CFA,∠CAF=180°-∠C-∠CFA,∠BEF=180°-∠B-∠BFE,∠CAB=20°,∴∠BEF=∠CAB=20°,∴∠DEF=180°-∠BEF=180°-20°=160°.本节内容与图形是紧密相连的,图形也是学生非常喜欢的,所以本节课的引入,重点以图形为主,既让学生感受到学数学的乐趣,又引发了学生学习本节课的信心,并且对学生更加热爱生活、找到数学与生活实际的联系起到了非常重要的作用.本节课的另外一个特点是图形的平移、翻折与旋转,要求学生具有空间想象能力,这既是数学的美,也是一些学生感到吃力的地方,为了突破难点,在教学设计上,引入了几何画板,进行动态演示,让学生能在非常生动、精彩的课件中找到自信,另外,也为他们日后的学习起到了重要的铺垫作用.本节课中,全等形、全等三角形的定义都是比较浅显的,学生们非常容易接受,本节的难点是全等三角形的书写及找出对应边、对应角,在突破难点上,讲解没有达到非常生动.让学生在非常欢乐的气氛中达到难点突破是我们的教学目标.为了能突破难点,在设计上可先让学生拿着自己制作好的两个全等三角形进行平移、翻折与旋转,观察前后的变化,同时写出每次变换后的对应边、对应角,可同桌之间互相考察,也可一名学生指派另一名学生答题,然后老师再用几何画板进行动态演示,把实际操作逐步变为头脑中的印象,最后达到不用任何辅助手段就能在头脑中达到上述目的.练习(教材第32页)1.解:图(2)中,AB和DB,BC和BC,AC和DC是对应边;∠A和∠D,∠ABC和∠DBC,∠ACB和∠DCB是对应角.图(3)中,AB和AD,BC和DE,AC和AE是对应边;∠BAC和∠DAE,∠B和∠D,∠C和∠E是对应角.2.解:相等的边:AC=DB,OA=OD,OC=OB;相等的角:∠A=∠D,∠C=∠B,∠AOC=∠DOB.习题12.1(教材第33页)1.解:AC和CA是对应边;∠B和∠D,∠BAC和∠DCA,∠BCA和∠DAC是对应角.2.解:其他对应边:AN和AM,BN和CM,其他对应角:∠ANB和∠AMC,∠BAN 和∠CAM.3.解:∵三角形内角和为180°,∴a所对的角为180°-60°-54°=66°,又∵两个三角形全等,∴∠1=66°.4.解:(1)其他对应边:EF和NM,FG和MH,EG和NH;其他对应角:∠E和∠N,∠FGE和∠MHN. (2)因为ΔEFG≌ΔNMH,所以NM=EF=2.1cm,EG=NH=3.3 cm,所以HG=EG-EH=3.3-1.1=2.2(cm),所以线段NM的长度是2.1 cm,线段HG的长度是2.2 cm.5.解:∠ACD和∠BCE相等.因为ΔABC≌ΔDEC,所以∠ACB=∠DCE.又因为∠ACB=∠ACE+∠BCE,∠DCE=∠ACD+∠ACE,所以∠ACD=∠BCE.6.解:(1)对应边:AE和AD,AC和AB,EC和DB;对应角:∠A和∠A,∠AEC和∠ADB,∠ACE和∠ABD. (2)因为ΔAEC≌ΔADB,所以∠ACE=∠ABD.又因为∠×(180°-1=∠2,所以∠ACE+∠2=∠ABD+∠1,即∠ACB=∠ABC,所以∠ABC=12∠A)=65°,所以∠1=∠ABC-∠ABD=65°-39°=26°.如图所示,ΔEFG≌ΔNHM,在ΔEFG中,FG是最长的边,在ΔNHM 中,MH是最长的边,∠F和∠NHM是对应角,且EF=2.4 cm,FH=1.9cm,HM=3.5 cm.(1)写出对应相等的边及对应相等的角;(2)求线段GN及线段HG的长度.〔解析〕(1)由于ΔEFG≌ΔNHM,根据两个三角形的最长边是对应边可知FG与MH对应相等,又∠F和∠NHM是对应角,所以∠FGE和∠HMN对应相等,剩下的一对角∠E和∠N也就对应相等了;进而根据对应顶点的关系可得到EF与HN对应相等,EG与MN对应相等;(2)由HM=3.5 cm可得它的对应边FG=3.5 cm,根据FH=1.9 cm可求得HG=FG-FH=1.6 cm;又由EF=2.4 cm可得它的对应边HN的长也是2.4 cm,则GN=2.4-1.6=0.8(cm).解:(1)对应相等的边有:FG=MH,EF=HN,EG=NM;对应相等的角有:∠F=∠NHM,∠E=∠N,∠EGF=∠M.(2)根据全等三角形的性质,得HN=EF=2.4cm,HG=FG-FH=HM-FH=3.5-1.9=1.6(cm),GN=HN-HG=2.4-1.6=0.8(c m).如图所示,A,D,E三点在同一直线上,且ΔBAD≌ΔACE.(1)试说明BD=DE+CE;(2)ΔABD满足什么条件时,BD∥CE?〔解析〕(1)要说明BD=DE+CE,由于ΔBAD≌ΔACE,所以BD和AE相等,因此我们只需说明AE=DE+CE即可,又AE=AD+DE,所以本题只需说明AD=CE即可,而这对线段恰好是全等三角形的对应边.(2)要使BD∥CE,则必须有∠BDE=∠E,根据全等三角形的对应角相等可知∠ADB=∠E,所以需要条件∠ADB=90°.解:(1)∵ΔBAD≌ΔACE,∴BD=AE,AD=CE,∵AE=AD+DE,∴BD=DE+CE.(2)当ΔABD满足∠ADB=90°时,BD∥CE.〔解题策略〕证明形如“BD=DE+CE”的问题有两种思路:思路一是将BD拆成两段,证明这两段分别等于DE和CE;思路二是找一条等于DE+CE 的线段,然后证明该线段等于BD.12.2三角形全等的判定1.熟练掌握“边边边”定理、“边角边”定理、“角边角”定理、“角角边”定理、“斜边直角边”定理.2.会用这些判定方法判定两个三角形全等.1.让学生通过分类讨论和作图的方法探索三角形全等的判定定理,并让学生用运动变换的方法证实.2.在探索全等三角形的判定方法的过程中,渗透分类讨论的思想.3.培养学生观察、概括、归纳的能力.1.让学生体验分类的思想,培养学生的合作精神.2.培养学生学习数学的兴趣,体会研究问题的思想和方法.【重点】全等三角形的判定方法.【难点】能用全等三角形的判定方法判定两个三角形全等.第课时1.掌握“边边边”定理的内容.2.能初步应用“边边边”定理判定两个三角形全等.3.会作一个角等于已知角.让学生探索三角形全等的条件,体验用操作、归纳得出数学结论的过程.通过探究三角形全等的条件的活动,培养学生合作交流的意识和大胆猜想、乐于探索的良好品质,以及发现问题的能力.【重点】“边边边”定理.【难点】探索三角形全等的条件.【教师准备】多媒体课件.【学生准备】复习全等三角形的性质,准备直尺和圆规.导入一:【提出问题】(1)全等三角形相等,相等.(2)已知ΔAOC≌ΔBOD,则∠A=∠B,∠C=,AC=,=OB,=OD.[设计意图]通过复习让学生进一步掌握全等三角形的性质,为下一步学习全等三角形的判定打下基础.导入二:通过前面的学习我们知道,如果两个三角形具备三条边和三个角分别对应相等,那么这两个三角形一定全等.但是要想画一个三角形与已知的三角形全等一定需要六个条件吗?条件能否尽可能地少呢?一个条件行吗?两个条件呢?一、探究三角形全等的条件【学生活动一】(1)只给一个条件(一条边或一个角)画三角形时,画出的三角形一定全等吗?(2)如果给出两个条件呢?给出两个条件画三角形时,有几种可能的情况,每种情况下作出的三角形一定全等吗?学生讨论有几种可能的情况,然后按照下面条件画一画:①三角形一个内角是30°,一条边是3 cm;②三角形两个内角分别是30°和50°;③三角形的两条边分别是4 cm和6 cm.学生分组讨论、画图、探索、归纳,最后以组为单位出示结果.【结果展示】(1)只给定一条边时.只给定一个角时.(2)给出的两个条件可能是:一边一内角、两内角、两边.可以发现按这些条件画出的三角形都不能保证一定全等.【议一议】如果给出三个条件画三角形时,你能说出有几种情况吗?(三条边,两条边一个角,一条边两个角,三个角)在刚才的探索过程中,我们已经发现已知三内角不能保证两个三角形全等.下面我们就来逐一探索其余的三种情况.(这节课只讨论第一种情况)【学生活动二】拼一拼.用你们准备的4 cm,5 cm,7 cm长的三根细木棒拼一个三角形,与其他同学拼成的三角形比较,它们一定全等吗?你又发现了什么?以小组为单位,把拼好的三角形画在纸上并剪下来,再把剪下的三角形重叠在一起,发现都能够重合,这说明这些三角形都是全等的.二、探究运用“SSS”判定两个三角形全等思路一【出示问题】先任意画一个ΔABC,再画一个ΔA'B'C',使得A'B'=AB,B'C'=BC,A'C'=AC,把画出的ΔA'B'C'剪下来,放在ΔABC上,看它们能完全重合吗?(即全等吗?)【学生活动】拿出直尺和圆规,按上面的要求作图并验证.画法:(1)画B'C'=BC;(2)分别以点B',C'为圆心,线段AB,AC的长为半径画弧,两弧相交于点A';(3)连接A'B',A'C'.【教师活动】巡视、指导、引入课题,这个作图的结果反映了什么规律?【学生活动】在思考、实践的基础上,归纳出判定三角形全等的方法.【教师板演】三边分别相等的两个三角形全等(可以简写成“边边边”或“SSS”).[设计意图]通过学生画图、观察、比较、思考等活动,一步一步地探索出结论,感悟基本事实的正确性,在概括基本事实的过程中,引导学生透过现象看本质,锻炼学生用数学语言概括结论的能力,同时也增加了学生的数学体验,让他们充分感受到成功的喜悦.思路二。

第十二章催眠治疗法第一节催眠疗法概述一、什么是催眠（一）催眠的涵义催眠（hypnosis）是一种类似睡眠而实非睡眠的意识恍惚状态。

此种恍惚的意识状态，是在一种特殊情境之下，经由催眠师的诱导而形成的，它与正常睡眠是有区别的。

催眠状态是由催眠师用暗示的方法引出来的。

人在催眠状态下，生理与心理都发生着特殊的变化，人的意识高度集中，只与催眠师保持单线联系，对其他事物没有反应，完全放心地接受催眠师的引导。

（二）催眠的功能（或效应）1、生理效应：（1）影响植物神经功能（2）可定向调整机体功能（3）催眠僵体效应。

2、心理效应：（1）思维自主性减低（2）暗示性上升（3）注意范围狭窄（4）记忆变化（增强或遗忘）（5）催眠性幻觉（6）催眠逻辑（7）时间曲解（8）返童与速老（9）回忆“前生”（10）催眠后行为（11）催眠性痛觉丧失（12）隐蔽的观察者（意识分离状态）（三）催眠状态的层次分析1、轻度催眠状态。

轻度催眠状态，即是一种浅程度的催眠状态。

这一状态的实验结果是“观念运动”学说的基础。

“观念引起运动，运动加强观念”。

通过暗示适当地加以诱导，观念运动就会加强，同时，也越来越容易施加暗示、出现所谓的“被暗示性的亢进”现象。

这个层次的催眠状态对患者的选择性不高，一般的人都能在长则数分钟，短则—分钟内进入这一状态。

轻度的催眠现象我们在平时生活中就可以见到，例如人们称之为“发呆”“出神”的现象即是如此，少年儿童最多见，所以说对少年易施加催眠术，这与他们的思想单纯、情感体验肤浅有关。

2、中度催眠状态。

轻度催眠状态以后，如果进一步引向深入，就会出现一些特定的生理反常现象，我们就说他已经进入中度催眠状态。

中度催眠状态的特征：（1）感觉迟钝或感觉过敏。

通过暗示能明显地支配感觉。

只不过，若不施加任何暗示，在催眠中感觉一般是迟钝的，任何感觉器官都会变得迟钝起来。

例如，此时针刺他的手背皮肤，几乎看不到他有痛苦的表情，手也没有回避性的条件反射。

第一章绪论一、名词解释总体个体样本样本含量随机样本参数统计量准确性精确性二、简答题1、什么是生物统计？它在畜牧、水产科学研究中有何作用？2、统计分析的两个特点是什么？3、如何提高试验的准确性与精确性？4、如何控制、降低随机误差，避免系统误差？第二章资料的整理一、名词解释数量性状资料质量性状资料半定量（等级）资料计数资料计量资料二、简答题1、资料可以分为哪几类？它们有何区别与联系？2、为什么要对资料进行整理？对于计量资料，整理的基本步骤怎样？3、在对计量资料进行整理时，为什么第一组的组中值以接近或等于资料中的最小值为好？4、统计表与统计图有何用途？常用统计图、统计表有哪些？第三章平均数、标准差与变异系数一、名词解释算术平均数几何平均数中位数众数调和平均数标准差方差离均差的平方和（平方和）变异系数二、简答题1、生物统计中常用的平均数有几种？各在什么情况下应用？2、算术平均数有哪些基本性质？3、标准差有哪些特性？4、为什么变异系数要与平均数、标准差配合使用？三、计算题1、10头母猪第一胎的产仔数分别为：9、8、7、10、12、10、11、14、8、9头。

试计算这10头母猪第一胎产仔数的平均数、标准差和变异系数。

2、随机测量了某品种120头6月龄母猪的体长，经整理得到如下次数分布表。

试利用加权法计算其平均数、标准差与变异系数。

组别组中值（x）次数（f）80— 84 288— 92 1096— 100 29104— 108 28112— 116 20120— 124 15128— 132 13136— 140 33、某年某猪场发生猪瘟病，测得10头猪的潜伏期分别为2、2、3、3、4、4、4、5、9、12(天)。

试求潜伏期的中位数。

4、某良种羊群1995—2000年六个年度分别为240、320、360、400、420、450只，试求该良种羊群的年平均增长率。

5、某保种牛场，由于各方面原因使得保种牛群世代规模发生波动，连续5个世代的规模分别为：120、130、140、120、110头。