一阶线性电路的三要素法

WORD 格式.分享方法一阶电路的三要素法一阶电路是指含有一个储能元件的电路。

一阶电路的瞬态过程是电路变量有初始值按指数规律趋向新的稳态值，趋向新稳态值的速度与时间常数有关。

其瞬态过程的通式为f (t ) = f (∞) + [ f (0+) – f (∞)]τt-e式中：f (0+) —— 瞬态变量的初始值； f (∞) —— 瞬态变量的稳态值； τ —— 电路的时间常数。

可见，只要求出f (0+)、f (∞)和 τ 就可写出瞬态过程的表达式。

把f (0+)、f (∞)和 τ 称为三要素，这种方法称三要素法。

如RC 串联电路的电容充电过程，u C (0+) = 0， u C (∞) = E ， τ = RC ，则u C (t)= u C (∞)+[ u C (0+) − u C (∞)]τt-e结果与理论推导的完全相同，关键是三要素的计算。

f (0+)由换路定律求得，f (∞)是电容相当于开路，电感相当于短路时求得的新稳态值。

τ = RC 或RL=τ，R 为换路后从储能元件两端看进去的电阻。

三个要素的意义：(1) 稳态值f (∞)：换路后，电路达到新稳态时的电压或电流值。

当直流电路处于稳态时,电路的处理方法是：电容开路，电感短路，用求稳态电路的方法求出所求量的新稳态值。

(2) 初始值f (0+)：f (0+)是指任意元件上的电压或电流的初始值。

(3) 时间常数τ：用来表征暂态过程进行快慢的参数，单位为秒。

它的意义在于，a. τ越大，暂态过程的速度越慢，τ越小，暂态过程的速度则越快，b.理论上，当t 为无穷大时，暂态过程结束；实际中，当t =(3～5)τ时，即可认为暂态过程结束。

时间常数的求法是：对于RC 电路τ=RC ，对于RL 电路τ=L/R 。

这里R 、L 、C 都是等效值，其中R 是把换路后的电路变成无源电路，从电容（或电感）两端看进去的等效电阻（同戴维宁定理求R 0的方法）。

c.同一电路中，各个电压、电流量的τ相同，充、放电的速度是相同的。

一阶微分电路
一阶微分电路，又称为一阶线性常微分方程的电路，是指描述电路的微分方程为一阶线性常微分方程的电路。

在这样的电路中，Laplace等效方程中是一个一阶的方程。

在分析一阶微分电路时，通常采用三要素法，即先求出微分方程的通解，然后根据初始条件确定通解的系数。

一阶微分电路中的动态元件可以用一阶微分方程来表示，求解该微分方程即可得到电路的响应。

在实际应用中，一阶微分电路可以用于描述RC电路、RL电路和RCL电路等。

这些电路的特点和应用场景各不相同，但都可以使用一阶微分方程来描述其动态行为。

以上内容仅供参考，如需更全面准确的信息，可以查阅电路相关书籍或咨询专业的电气工程师。

一阶动态电路的三要素法一阶动态电路是指电路中只有一个电感或一个电容元件的电路，在分析这种电路时可以使用三要素法。

三要素法是一种基本的电路分析方法，它利用电路中三个基本元件（电源、电感、电容）的电压或电流关系来描述电路中的动态行为。

在使用三要素法时，需要使用线性微分方程来描述电路中的电压和电流关系。

在使用三要素法时，需要按照以下步骤进行分析：1.画出电路图，并确定电路中的电压和电流的参考方向。

2.根据电路图和电压和电流的参考方向，写出电路中的基尔霍夫电流定律和基尔霍夫电压定律等式。

3.根据电路元件的特性方程，写出电感或电容元件的电流和电压之间的关系。

4.将基尔霍夫定律和元件特性方程联立，并进行求解，得到电路中的电流和电压随时间变化的函数关系。

5.根据所求得的电流和电压随时间变化的函数关系，来分析电路的动态行为。

在使用三要素法进行电路分析时，首先需要根据电路图和电压、电流的参考方向写出基尔霍夫定律方程，例如，在一个带有电感元件和电源的串联电路中，可以根据基尔霍夫电压定律写出方程：\[V_L-V_s=0\]其中\(V_L\)是电感元件的电压，\(V_s\)是电源的电压。

接下来，根据电感元件的特性方程写出电感元件的电流和电压之间的关系，例如：\[V_L = L \frac{di_L}{dt}\]其中\(L\)是电感元件的感值，\(di_L\)是电感元件的电流微分，\(dt\)是时间微分。

将基尔霍夫定律方程和元件特性方程联立，并进行求解，可以得到电路中的电流和电压随时间变化的函数关系。

例如，可以得到电感元件的电流随时间变化的函数关系：\[i_L(t) = \frac{V_s}{L} \cdot t + i_L(0)\]其中，\(i_L(0)\)是初始时刻电感元件的电流。

最后，根据所求得的电流和电压随时间变化的函数关系，来分析电路的动态行为。

例如，在一个带有电感元件和电源的串联电路中，可以根据电压随时间变化的函数关系来分析电路中电压的变化情况。

试谈电路教学中“一阶线性电路三要素法公式的表示方法”
一阶线性电路三要素法公式的表示方法是指利用电路中的三要素R、L和C，采用特定的电路结构，将电路中所有电流及电压之间的关系以数学形式表示出来。

此公式的研究历史十分悠久，可以追溯到1745年威廉·马歇尔的“差分方程”，他是第一个研究了线性电路的人，他把电路中各部分之间的关系用极端简化的形式表示出来，这样就可以很方便的用数学推导的方法得出各部分之间的关系，这也是一阶线性电路三要素法公式的基础。

一般而言，用一阶线性电路三要素法公式表示电路中所有电流及电压之间的关系时，我们首先要确定电路结构、有几个极点，然后把电路中每一个极点都建模为一个电压源，并根据电路的结构分析，写出电路中电压源之间的关系。

然后我们要把电路中的三大要素R、L和C抽象为一个个电路元件，这样我们就可以将电路中电流及电压之间的关系表示出来，也就是一阶线性电路三要素法公式了。

在实际应用中，一阶线性电路三要素法公式有着广泛的应用，可以用来分析电路中各部分之间的电压及电流关系，从而更加清楚的了解电路的工作原理，从而对电路的设计有更深入的认识。

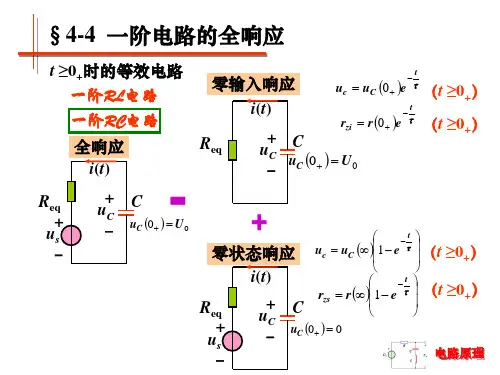
§5.4 一阶电路的全响应与三要素在上两节中分别研究了一阶电路的零输入响应和零状态响应，电路要么只有外激励源的作用，要么只存在非零的初始状态，分析过程相对简单。

本节将讨论既有非零初始状态，又有外激励源共同作用的一阶电路的响应，称为一阶电路的全响应。

5.4.1 RC 电路的全响应电路如图5-9所示，将开关S 闭合前，电容已经充电且电容电压0)0(U u c =-，在t=0时将开关S 闭合，直流电压源S U 作用于一阶RC 电路。

根据KVL ，此时电路方程可表示为：C u图 5-19 一阶RC 电路的全响应S C CU u tu RC=+d d （5-19） 根据换路原则，可知方程（5-19）的初始条件为 0)0()0(U u u C C ==-+令方程（5-9）的通解为 C CC u u u ''+'= 与一阶RC 电路的零状态响应类似，取换路后的稳定状态为方程的特解，则S CU u =' 同样令方程（5-9）对应的齐次微分方程的通解为τtCAe u -=''。

其中RC =τ为电路的时间常数，所以有τtS C AeU u -+=将初始条件与通解代入原方程，得到积分常数为 S U U A +=0所以电容电压最终可表示为τtS S c e U U U u --+=)(0 （5-20）电容充电电流为etS C R U U t u C i τ--==0d d这就是一阶RC 电路的全响应。

图5-20分别描述了s U ，0U 均大于零时，在0U U s >、0=s U 、0U U s <三种情况下c u 与i 的波形。

(a) (b)图5-20C u ，i 的波形图将式（5-20）重新调整后，得)1(0ττtS tC e U eU u ---+=从上式可以看出，右端第一项正是电路的零输入响应，第二项则是电路的零状态响应。

显然，RC 电路的全响应是零输入响应与零状态响应的叠加，即 全响应 = 零输入响应 + 零状态响应研究表明，线性电路的叠加定理不仅适用于RC 电路，在RC 电路的分析过程中同样适用，同时，对于n 阶电路也可应用叠加定理进行分析。

电工学━
知识点
1一阶暂态电路三要素法分析
1、三要素法分析
一阶暂态电路三要素，是指在求得f (∞)、f (0+)和τ（“三要素”）的基础上，可直接写出电路的响应（电压或电流），即
τ
t e
f f f t f -∞-++∞=)]()0([)()(2、注意事项（1）f （∞）的确定，求换路后电路中的电压或电流，其中电感视为短路，电容视为开路，即求解直流线性电路中电压或电流；（2）f （0+）的确定，与前面所属初始值的确定方法相同；（3）τ的确定，对于RC 和RL 电路，时间常数分别为τ=R 0C 和τ=L /R 0，其中R 0为电路换路后从储能元件两端求得的戴维南等效电阻；（4）三要素方法仅适应在阶跃激励下的一阶线性电路。

三元素法分析一阶电路的全响应电路论文学院：电子信息工程学院班级：电气091502班姓名：***学号：************三元素法分析一阶电路的全响应摘要：本文主要介绍用三元素法分析解决一阶电路问题。

用三元素法求一阶电路问题首先要求出三元素：初始值，稳态值，时间常数，用三元素法可以直接代入公式求解，求解过程简单。

关键词：一阶电路 三元素法一、 全响应定义当一个非零初始状态的一阶电路受到激励时，电路的响应称为一阶电路全响应。

全响应总是由初始值、特解和时间常数三个要素决定的。

二、 三元素法的基本原理一阶电路的数学模型是一阶线性微分方程： 其解答一般形式为：令 t = 0+ 全响应f （t ）的三要素求解公式为f （t ）=f （∞）＋[f （0+）－f （∞）]e －t/τ其中，f （0+）为t=0+时刻的初始值，f （∞）为t →∞时的特解稳态值，τ为t ≥0时的时间常数。

f （0+）、f （∞）和τ称为三要素。

只要知道f （0+）、f （∞）和τ这三个要素，就可以根据上述公式直接写出直流激励下一阶电路的全响应，这种方法称为三要素法。

三、 三元素法的解题步骤⒈ 求初始值 ⑴ 初始值定义t=0+时电路中电压与电流的值称为初始值。

⑵ 初始值的求解① 由换路前电路（稳定状态）求u C (0－)和i L (0－)； ② 由换路定律得 u C (0+) 和 i L (0+)。

③ 画0+等效电路。

c bf tfa=+d d τteA t f t f -+'=)()(a.换路后的电路b.电容（电感）用电压源（电流源）替代。

（取0+时刻值，方向与原假定的电容电压、电感电流方向相同）。

④由0+电路求所需各变量的0+值。

⒉求稳态值⑴稳态值的定义t=∞时电路中电压与电流的值称为稳态值。

⑵稳态值的求解稳态时，电容C视为开路，电感L视为短路，稳态值即求直流电阻性电路中的电压和电源。

⒊求时间常数τ⑴时间常数τ的定义当电阻的单位为Ω，电容的单位为F时，乘积RC的单位为s，称为RC电路的时间常数，用τ表示。

三要素法在一阶交流线性电路中的应用第l0卷第3期广东石油化工高等专科学校JOURNALOFGUANGD0GO0LLeGE20oO年8月OFTE(=}OLDGYV ol10No.3Aug20OO三要素法在一阶交流线性电路中的应用/刘利民,谢廖伟盛广东石油化工高等专科学幢自动化系.茂名525000嘉应大学钎理系,梅州514014f/,摘要该文分析三要素法在一阶直流线性电路暂态中的应用,从直流激励表达式推导交漉激励表达式关麓词倒加以证明.三要素法可以简化一阶交漉线性电路暂态分析.;坠;;竺塑钎嚼在一阶直流线性电路的经典分析中,对电路暂态过程各元件的响应(u,i),可以根据KCL,KVL和支路方程列出微分方程求解;也可以简单地利用三要素法求解[".但一般的电路书中,对于一阶交流线性电路,则采用解微分方程,或是利用相量法求解那么,三要素法是否同样适用于一阶交流线性电路.表达式又有些什么变化,下面对此加以分析.1一阶直流线性电路中的三要素电阻,电容,电感都是组成电路模型的理想元件,其中电阻是耗能元件,电容和电感本身不消耗能量,只与电源问进行能量的交换,是储能元件.仅含有一个储能元件或能等效为一个储能元件的电路称为一阶线性电路J.当一阶线性电路的结构或元件的参数发生变化时,可能使电路改变原来的工作状态,丽转变到另一工作状态,这种转变往往需要经历一个过程,在工程上称为过渡过程.在过渡过程的分析中特别要注意独立初始条件U(0+),IL(0+)(因为换路瞬问,电容两端电压不能突变,电感两端电流不能突变).根据换路时储能元件中是否储有能量又可分为零输入响应,零状态响应和全响应【3].如果输入激励为直流,如图1所示.图1直接激励下的RI奎响应当开关K由1扳到2时,可直接根据公式一求L的全响应收刚:2000—05一呻第一忭者:男.助教妾Il\48广东石油化工高等专科学校20oO年f(t):f(0o)+[f(0+)一f(o.)]e一其中:f(0o)是换路后的稳态值;f(o一)是换路后的初始值;r是时间常数此即为三要素2一阶交流线性电路的三要素.(1)一阶交流线性电路与一阶直流线性电路的唯一区别在于换路后的输人激励一个是交流,一个是直流,可分析方法一样,由此可推测交流也能采用公式(1),但由于是交流,在取值时应有所改变,下面分两种情况来具体讨论(1)RL串联电路,将图l中的u换成u=U=,sin(~t+)如图2:田2交流激励下的RlJ仝响应当K由l扳到2时电感L的响应iL,换路前:iL(0+)=U0/R换路后:iL(0+)=iL(0一)=/R根据KVL:UR+uL=u,由U=Ldd~ti则上式为:i【_R+L害=uSin(t)这是一个以iL为变量的一阶线性常系数非齐次方程.先求齐次方程iLR+Ldi=0通解iL=Ae一式中:A为待定系数,r=L/R用常数变易法求iL,即令iL=A(t)e代人(2)化简得LA(t)e=usin(~t+)故A(t)=兰et+B代人(3)得i.:磐+Be一一R+(∞L)'(2)(3)当t=0时_1I(0+)=LLl/R,即B=訾一令arcIan=【【.I/R化簖得i=垦+[+]e—t4+∞L)!~/+(c1.I)()=iL(t)+[iL(0+)一(0+)]evt/T式中_】lli(r)为换路后的稳态值;iT(0+)为换路后的初始疽;iI.(0)为换路后il(t)的初始值;r=L/R为时间常数(2)RC并联电路,如图3所示.is=lo,Nn(~t+.』,)第3期刘利民等:三要素在一阶交流线性电路中的应用49交流教尉下的RC奎响应分析当K由1扳到2时电容C的响应U比较图2和图3,可得,电压源U与电流源i互换,电容C与电感L互换,响应U与响应i【互换,电阻R与电导G的互换,电路由串联转换成并联.由此可根据电路中的对偶原理L4J,由上面分析的③式直接写出U的响应u-一+Uo—l.,州sin(tb-~z)』e_]式中:导纳角唾～=arctan~C/G导纳的摸JYI=√+(L)所以-二u(t)+[U(0+)一Uc(0+)】e一,r式中:U(t)为换路后的稳态值;U(0+)为换路后的初始值;U(0+)为换路后U(t)的初始值;r=C/G为时间常数由上分析.可以得出三要素法在一阶交流线性电路中同样适用,并可给出一阶交流线性电路的全响应一般表达式为下面式(5)f(t)=f(t)+[f(0+)一f(0+)]e(5)式中:f(t)为换路后的稳态值;f(0+)为换路后的韧始值;f(0+)为换路后f(t)的初始值;r 为时间常数其三要素为(1)稳态分量f(t).(2)初始值f(0+)和f(0+),(3)时间常数r.3下面以例题来说明上面推导公式的应用例l:电路如图2所示,已知外加电压Us=√2×220sln(314t十30.)V.Uo=60V.R=30CZ.L=0.2H.求开关K由J扳到2时电感L上的电流II_.解:利用上面的推导公式:iL=II_(t)+[iL(0+)一|1.(0+)】e其中:_l(0一)=it.(0+)=UJ/R:2A;时间常数t=L/R=6.67x10s;阻抗角arCtan:"】I./R=645.Jzf=√R+(叫L)=6960;.f"一尘=2一兰Q煎(!±:=鲢::),一69.6i『(O+)-=447sin(一34.5.)=一235A所以:__=447sin(3l434.5.)一035eA例2:电路如图3所示,已知~lqJn电-=2sin(3l4t+)A,Uo:3V,G:0IS,(::200,uF,求开关K由l扳到2时电容(上的电压U.解:利用上面的推导公式:U=u(t)+(u(0+)一u(0)]eI1其中:U(0一=U(0+)=3V;时间常数r:C/G:2×100s;导纳角中v=arctant,~IG=32.r广东石油化工高等专科学校2O00年IY}=~/G2+(c)=0.27SUc(t=芋型=74sin(314t+129.)VU'(O+)=74Nn(129.)=17V所以:U=74sin(314t+129.)一13e一rv综上所述,交流激励过渡过程的响应表达式与直流激励的过渡过程的响应表达式相似,但与直流激励的过渡过程不同的是,交流激励的过渡过程的响应不仅与储能元件的初始值有关,与交流激励的接人角有关,同时也与电路参数所确定的~o(RC并联电路中的导纳角,RL串联电路中的阻抗角)有关J.只要注意以上问题,采用公式(5)就可以大大简化一阶交流线性电路暂态过程的分析计算.邱美嚣.电路.北京:高等教育出敝社,1992184-185秦曾煌电工学北京:高等教育出簸祉,1998.242--245孙骆生电工学基车戟程北京:高等教育出颇社,1992.203蒋趋川屯工学北京:高等教育出敝杜.1988261--264谭j鼠鼎电工基础.北京:高等教育出版社,1992.IN--85参考文献Three——factormethodisusedinfirst——orderalternatingcurrentlinearcircuitLiuLimin,XieMan,LiaoWeishengAbstractThispaperanMyz~theusage0fthree—factormethodintransientstateoffirst—orderalternatingcurrentcircuit.gettingthealternating~iiTent—expre~ionfromdirectcurrentexpression,andprov~itbyex.amples.Thethree—factormethodcansimplifytheanalysisofthetransientstate0ffirst—orderalternatingcurrent1ineardrcuitKeywordsthree—factormethod;first—ordercircuit;transientstate;alternatingcurrentenergize;completeresponse。