RC电路响应和三要素法解读

一阶暂态电路三要素法和一阶暂态电路是指由电阻、电感和电容组成的电路，在初始状态下有一个初始电压或电流，当电路发生突变时，电压或电流会发生暂态响应。

为了研究电路的暂态响应，我们可以使用一阶暂态电路三要素法。

一阶暂态电路三要素法是一种用于分析一阶暂态电路响应的方法，它通过确定电路的三个要素：时间常数、初始条件和输入信号来推导电路的暂态响应。

时间常数是一阶暂态电路的一个重要参数，它描述了电路响应的速度。

对于由电阻R和电容C组成的一阶电路，时间常数τ可以通过以下公式计算：τ = RC。

时间常数越小，电路的响应速度越快。

初始条件是指在初始状态下电路的电压或电流值。

在分析一阶暂态电路时，我们需要知道电路在初始时间点的电压或电流值，这些值可以通过测量或已知条件来确定。

输入信号是指施加在电路上的信号。

输入信号可以是电压或电流的变化，它会引起电路的响应。

在分析一阶暂态电路时，我们需要知道输入信号的形式和参数，例如输入信号的幅值、频率和相位。

通过确定时间常数、初始条件和输入信号，我们可以使用一阶暂态电路三要素法来推导电路的暂态响应。

首先，我们可以根据时间常数来判断电路的响应速度。

如果时间常数很小，电路的响应会很快；如果时间常数很大，电路的响应会比较慢。

我们可以根据初始条件来确定电路的初始状态。

初始条件可以是电路的初始电压或电流值。

通过测量或已知条件，我们可以确定电路在初始时间点的初始条件。

我们可以根据输入信号的形式和参数来计算电路的暂态响应。

根据输入信号的幅值、频率和相位，我们可以计算出电路在不同时间点的电压或电流值。

总结一下，一阶暂态电路三要素法是一种用于分析一阶暂态电路响应的方法。

通过确定时间常数、初始条件和输入信号，我们可以推导出电路的暂态响应。

这种方法可以帮助我们更好地理解和分析一阶暂态电路的行为，对于工程实践中的电路设计和故障排除非常有用。

一阶RC电路的暂态过程 - 电子技术分析一阶RC电路的暂态过程的方法有很多种，这里只介绍经典法和三要素法，下面以图3-6所示的电路为例，对这两种方法分别进行介绍。

1、经典法图3-6所示电路，t=0时开关S闭合，电源对电容充电，从而产生过渡过程。

根据KVL，得回路电压方程为而：从而得微分方程：此微分方程的通解为两个部分：一个是特解，一个是齐次方程式的解，即:特解可以是满足方程式的任何一个解，假定换路后，t→时电路已达稳定，电容C的电压为稳态分量，那么它是满足方程式的一个解。

对于图3－6所示的RC串联电路：=＝US。

微分方程的齐次方程式为：令其通解为，代入齐次微分方程式可得特征方程式是：所以，特征方程式的根为：式中，其量纲为（秒），称为电路暂态过程的时间常数。

因此微分方程的通解=+积分常数A需用初始条件来确定。

在t=0时=+=+A由此可得：A=-因此+上述利用微分方程进行求解分析一阶RC电路的暂态过程的方法称为经典法，经典分析法步骤较多，为便于掌握，现归纳如下：（1）用基尔霍夫定律列出换路后电路的微分方程式。

（2）解微分方程。

解微分方程通常比较麻烦，对于一阶RC电路有一种更方便、更常用的分析方法——三要素法。

2、三要素法通过经典分析法我们得到图3-6所示电路暂态过程中电容电压为： +上述结果可归纳为一种简单的解题方法，称为“三要素法”，式中只要知道稳态值，初始值和时间常数，这“三要素”，则便被唯一确定。

这种利用“三要素”来实现电路暂态分析的方法，称“三要素法”。

虽然上述式子由图3-6所示的电路提出，但它适合于任何含一个储能元件的一阶电路在阶跃（或直流）信号激励下的过程分析。

而经典法则适用于任何线性电路的暂态分析。

在“三要素”中，特别要注意时间常数，前面已定义，一阶RC电路仅有一个电容元件，C即为电容器的电容量，而R为换路后的电路中除去电容后所得无源二端口网络等值电阻。

下面以直流(激励源为常数)一阶电路为例应用“三要素法”分析电路的响应。

3.3 RC电路的响应经典法分析电路的暂态过程，就是根据激励通过求解电路的微分方程以得出电路的响应。

激励和响应都是时间的函数所以这种分析又叫时域分析。

3.3.1 RC电路的零输入响应零输入响应------无电源激励，输入信号为零。

在此条件下，由电容元件的初始状态u C（0+）所产生的电路的响应。

分析RC电路的零输入响应，实际上就是分析它的放电过程。

如图 3.3.1(RC串联电路，电源电压U0)。

换路前，开关S合在位置2上，电源对电容充电。

t=0时将开关从位置2合到位置1，使电路脱离电源，输入信号为零。

此时，电容已储有能量，其上电压的初始值u C（0+）=U0；于是电容经过电阻R开始放电。

根据基尔霍夫电压定律，列出t≥0时的电路微分方程RCdu C/dt+u C=0 3.3.1式中 i=Cdu C/dt令式 3.3.1的通解为 u C=Ae pt代入3.3.1并消去公因子Ae pt得微分方程的特征方程 RCp+1=0 其根为p=-1/RC于是式3.3.1的通解为 u C=Ae-1t/RC定积分常数A。

根据换路定则，在t=0+时，u C（0+）=U0，则A=U0。

所以 u C= U0e-1t/RC= U0 e-1/τ ------ 3.3.3 C图3.3.1RC放电电路-+-U+u C-t=0+u CSiR其随时间变化的曲线如图3.3.2所示。

它的初始值为U 0，按指数规律衰减而趋于零。

式3.3.3中，τ=RC 它具有时间的量纲，所以称电路时间常数。

决定u C 衰减的快慢。

当t=τ时， u C = U 0e -1=U 0/2.718=36.8%U 0 可见τ等于电压u C 衰减到初始值U 0的36.8%所需的时间。

可以用数学证明，指数曲线上任意点的次切距的长度都等于τ。

以初始点为例〖图3.3.2（a ）〗du C /dt=-U 0/τ 即过初始点的切线与横轴相交于τ。

从理论上讲，电路只有经过t=∞的时间才能达到稳定。

电路分析基础实验三：RC电路三要素法
实验报告
实验目的：
- 了解RC电路的基本原理和特性
- 研究如何使用三要素法对RC电路进行分析
- 进行实验验证和数据记录
实验材料：
- 电源（直流电源或函数信号发生器）
- 电阻（R）
- 电容（C）
- 测量仪器（示波器、万用表等）
实验步骤：
1. 搭建RC电路，将电阻和电容连接起来。

2. 连接电源，并调节合适的电压或频率。

3. 使用示波器观察电压波形，记录数据。

4. 使用万用表测量电阻和电容的值。

5. 根据实验数据分析RC电路的响应和特性。

实验结果：
根据实验数据，可以得出RC电路的响应曲线随时间变化的规律。

具体结果如下：
- 电压随时间指数衰减，呈指数函数的形式。

- 在RC电路中，电容充电和放电的时间常数与电阻和电容的
数值相关。

- 当电阻或电容的数值增加时，充电/放电时间常数增加，电路
响应的时间变慢。

结论：
通过RC电路三要素法实验，我们了解了RC电路的基本特性
和响应规律。

电阻和电容的数值对电路的响应时间有直接影响，加
深了对RC电路的认识和分析能力。

注意事项：
- 在实验过程中，要注意电路搭建的正确性和安全操作。

- 记录数据时要准确并详细，以便后续分析和实验结果的验证。

- 实验结束后，及时整理实验数据和结果，做好实验报告。

参考文献：
[1] xxx
[2] xxx。

rc电路的三要素法RC电路是由电阻（R）和电容（C）组成的电路。

在RC电路中，电容器充电和放电的过程受到电阻的影响。

为了分析RC电路的特性和行为，我们可以借助三要素法。

三要素法是一种用于分析电路的方法，它将电路分解为三个要素：电源、电容和电阻。

通过研究这三个要素之间的相互作用，可以更好地理解RC电路的行为。

我们来看电源。

电源是RC电路中的能量来源，它提供电流。

在RC 电路中，电源的电压可以是直流或交流。

直流电压是恒定的，而交流电压则是周期性变化的。

电源的电压决定了电容器充电和放电的速度。

接下来，我们来看电容。

电容是RC电路中的一个关键元件，它可以存储电荷并产生电场。

电容器由两个导体板和介质组成，当电源施加电压时，电荷会在导体板之间积累。

电容器的容量越大，它存储和释放电荷的能力就越强。

电容器的充电和放电过程取决于电源的电压和电阻。

我们来看电阻。

电阻是RC电路中的另一个关键元件，它限制电流的流动。

电阻的大小决定了电容器充电和放电的速度。

当电容器充电时，电阻限制了电流的流动，使得电荷积累在电容器上。

当电容器放电时，电阻同样限制了电流的流动，使得电荷从电容器中释放出来。

通过三要素法，我们可以更好地理解RC电路的行为。

当电源施加电压时，电容器开始充电。

充电过程中，电容器的电压逐渐增加，直到达到电源电压。

充电的速度取决于电源的电压和电阻的大小。

一旦电容器充满电荷，电容器将无法再吸收更多的电荷。

当电源停止施加电压时，电容器开始放电。

放电过程中，电容器的电压逐渐下降，直到与电源电压相等。

放电的速度同样取决于电源的电压和电阻的大小。

一旦电容器释放完所有电荷，电容器将不再具有电压。

通过三要素法，我们可以分析RC电路的特性和行为。

通过调整电源的电压、电容器的容量和电阻的大小，我们可以控制电容器充电和放电的速度。

这对于设计和优化RC电路非常重要。

总结一下，RC电路是由电阻和电容组成的电路。

通过三要素法，我们可以更好地理解RC电路的特性和行为。

rc电路的全响应RC电路是由电阻（R）和电容（C）组成的一种电路，其全响应是指电路中电压或电流随时间变化的总和。

全响应的求解对于理解RC电路的行为具有重要意义，尤其是在电子工程学和通信工程学中。

当一个RC电路被连接到一个电源上时，电路中的电压或电流将随时间的推移而发生变化。

理解RC电路的响应方式非常有用，可以帮助我们设计与操控该电路，也可以了解其如何与其他元件相互作用。

一个RC电路的全响应由两个部分组成：自由响应和强制响应。

自由响应是当电路断开电源时电容器内储存电荷以及在电容器与电阻中储存的能量导致的电压或电流的变化。

强制响应是由于输入的电磁场而引起的电压或电流的变化。

在一个RC电路中，电压或电流的变化速度取决于电容的大小以及电阻的阻值。

当电容越大时，电路的响应速度就越慢，因为电流在电容器中充电和放电所需要的时间更长。

相反，当电阻的阻值越大时，电路的响应速度就越快，因为电容器在电阻中放电所需要的时间更短。

此外，对于一个RC电路来说，其全响应将受到外部信号的影响。

这些外部信号可以是干扰，也可以是电源信号。

因此，RC电路可以通过选择不同的电容和电阻值来实现不同的响应速度，并且可以通过改变输入电压或电流来控制其响应。

最后，值得注意的是，一个RC电路的全响应也可以通过数学模型计算得出，这对于电子工程师和通信工程师来说非常重要。

通过数学模型，我们可以精确地计算出电路的响应，并对其进行优化和设计。

总之，RC电路的全响应是不可或缺的，它可以帮助我们更好地理解电路的行为，从而更好地利用该电路。

因此，对于任何对电子工程或通信工程感兴趣的人来说，了解RC电路的全响应是非常重要的。

9 RC 一阶电路（动态特性 频率响应）一个电阻和一个电容串联起来的RC 电路看起来是很简单的电路。

实际上其中的现象已经相当复杂，这些现象涉及到的概念和分析方法，是电子电路中随处要用到的，务必仔细领悟。

9.1 零输入响应1.电容上电压的过渡过程先从数学上最简单的情形来看RC 电路的特性。

在图9.1 中，描述了问题的物理模型。

假定RC 电路接在一个电压值为V 的直流电源上很长的时间了，电容上的电压已与电源相等（关于充电的过程在后面讲解），在某时刻t 0突然将电阻左端S 接地，此后电容上的电压会怎么变化呢？应该是进入了图中表示的放电状态。

理论分析时，将时刻t 0取作时间的零点。

数学上要解一个满足初值条件的微分方程。

看放电的电路图，设电容上的电压为v C ,则电路中电流dt dv C i C =， 依据KVL 定律，建立电路方程：0=+dt dv RCv C C初值条件是 ()V v C =0 像上面电路方程这样右边等于零的微分方程称为齐次方程。

设其解是一个指数函数： ()t C e t v S K =K 和S 是待定常数。

代入齐次方程得 0=KS +K S S t t eRC e约去相同部分得 0=S +1RC 于是 RC 1-=S齐次方程通解 ()RC tC e t v -K =还有一个待定常数K 要由初值条件来定： ()V K Ke v C ===00最后得到： ()τt RCt C Ve Vet v --== 在上式中，引入记号RC =τ，这是一个由电路元件参数决定的参数，称为时间常数。

它有什么物理意义呢？在时间t = τ 处， ()V V Ve v 0.368=e ==-1-C τττ 时间常数 τ是电容上电压下降到初始值的1/e ＝36.8% 经历的时间。

当t = 4 τ 时，()V v 0183.0=4C τ，已经很小，一般认为电路进入稳态。

数学上描述上述物理过程可用分段描述的方式，如图9.1 中表示的由V 到0的“阶跃波”的输入信号，取开始突变的时间作为时间的0点，可以描述为：()()0=S ≤t V t v 对 ；()()00=S ≥t t v 对。

电路分析基础实验三RC电路三要素法实验报告一、实验目的1.了解RC电路三要素法的基本原理；2.学习使用瞬态响应测量电路的方法；3.掌握实验仪器的使用方法。

二、实验器材和测量设备1.函数信号发生器2.直流电源3.示波器4.万用表5.电阻（10kΩ）6.电容（1μF）7.电感（可选）三、实验原理RC电路是由电阻（R）和电容（C）组成的，是一种常见的电子元件。

根据电路中的电压和电流的变化规律，可以把RC电路分为充电、放电、稳态三个阶段。

1.充电阶段：当RC电路接通电源时，电容开始充电，电流逐渐变小。

2.放电阶段：当电压达到峰值后，电容开始放电，电流逐渐变大。

3.稳态阶段：经过一段时间后，电路达到稳态，电容的电压和电流保持不变。

通过测量充电曲线和放电曲线，可以了解RC电路的特性。

四、实验内容1.搭建RC电路：按照实验方案搭建RC电路。

2.设置函数信号发生器：选择合适的频率和幅值，使电压波形适合测量。

3.设置示波器：将示波器接入电路，调节示波器参数，观察电压和电流波形。

4.测量曲线：分别测量充电曲线和放电曲线，并记录数据。

5.计算：根据测量数据，计算RC电路的电阻和电容值。

五、实验步骤1.搭建RC电路：将电阻和电容按照实验方案连接起来。

2.设置函数信号发生器：选择合适的频率和幅值，并输入到电路中。

3.设置示波器：将示波器接入电路中，调节示波器参数，使得波形清晰可见。

4.测量曲线：观察充电曲线和放电曲线，并用示波器测量电压和电流数据。

5.计算：根据测量数据，计算RC电路的电阻和电容值。

六、实验结果根据实验测量得到的数据，绘制RC电路的充电曲线和放电曲线。

根据曲线拟合的结果，计算出RC电路的电阻和电容值。

七、实验讨论2.如何减小误差，提高实验精度？八、实验总结通过本次实验，我了解了RC电路三要素法的基本原理，学会了使用瞬态响应测量电路的方法，掌握了实验仪器的使用方法。

通过实际操作和数据分析，我对RC电路的特性有了更深入的认识，并且提高了实验技能。

3.4一阶线性电路暂态分析的三要素法只含有一个储能元件或可等效为一个储能元件的线性电路，不论是简单的或复杂的，它的微分方程都是一阶常系数线性微分方程这种电路称为一阶线性电路。

上述的RC 电路是一阶线性电路，电路的响应是由稳态分量（包括零值）和暂态分量两部分相加而得，如写成一般式子，则为f （t ）= f ′（t ）+ f ″（t ）= f （∞）+A e -t/τ式中 f （t ）是电流或电压，f （∞）是稳态分量，A e -t/τ是暂态分量。

若初始值为 f （0+）， 则得 A=f （0+）-f （∞） 于是f （t ）= f （∞）+［f （0+）-f （∞）］e -t/τ 这就是分析一阶线性电路的暂态过程中任意变量的一般公式［式（3.3.11）中变量是u C ］。

只要求得f （0+）、f （∞）和τ这三个 “要素”，就能直接写出电路的响应。

至于电路响应的变化曲线，如图3.4.1所示，都是按指数规律变化的（增长或衰减）。

下面举例说明三要素法的应用。

例3.4.1应用三要素法求例3.3.3中的u C 。

例3.4.2求图3.4.2（a ）所示电路在t ≥0时的u 0和u C 。

设u C （0-）=0。

例3.4.3在图3.4.3中，U=20v ，C=4uF, R=50k Ω。

在t=0时闭合S 1，在f(∞)f(∞)图3.4.1f(t)的变化曲线(c)f(∞)=0τOOt(c)f(∞)≠0t τ（b ）f(0+)≠0（a ）f(0+)=0f(0+)f(∞)f(0+)f（t ）f（t ）τOOtf(0+)τt f（t ）f（t ）t=0.1s时闭合S2，求闭合后的电压u R。

设u C（0-）=0。

例3.4.4在图3.4.4（a）的电容分压电路中，设u C1（0-）= u C2（0-）=0，试求t≥0时的u C1或u C2。

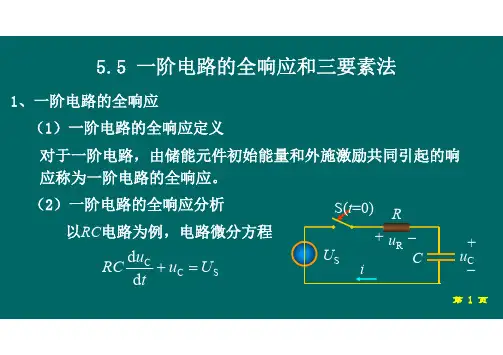
RC电路的全响应
RC电路同时具有初始储能和电源激励条件下的响应称作电路全响应。

计算电路全响应与计算零状态响应一样，都可通过求解电路的微分方程得出，也可以用“三要素法”进行分析，不同的只是电路有初始储能。

用“三要素法”通常更加方便，下面的例子用“三要素法”进行分析。

例1电路如图3-13所示，
时已处于稳态。

时开关闭合，试求电容元件两端
电压（t）和电流。

解：时已处于稳态，
即电容的初始电压为换路前电容的开路电压
uC(0-)=
根据换路定律，电容电压的初始值uC(0+)=uC(0-)=6V
t=时，稳态值为换路后电容的开路电压，因此
时间常数，其中R为换路后的电路从电容端看无源二端网络的等值电阻。

+
=
uC及iC的波形图如图3-14所示。

例2电路如图3-15所示，
换路前已处于稳态，时开关闭合，试求换路后（）的。

解：换路前（）时
换路后
达稳定时
时间常数
于是。