3-7 一阶电路的三要素法

一阶暂态电路三要素法和一阶暂态电路是指由电阻、电感和电容组成的电路，在初始状态下有一个初始电压或电流，当电路发生突变时，电压或电流会发生暂态响应。

为了研究电路的暂态响应，我们可以使用一阶暂态电路三要素法。

一阶暂态电路三要素法是一种用于分析一阶暂态电路响应的方法，它通过确定电路的三个要素：时间常数、初始条件和输入信号来推导电路的暂态响应。

时间常数是一阶暂态电路的一个重要参数，它描述了电路响应的速度。

对于由电阻R和电容C组成的一阶电路，时间常数τ可以通过以下公式计算：τ = RC。

时间常数越小，电路的响应速度越快。

初始条件是指在初始状态下电路的电压或电流值。

在分析一阶暂态电路时，我们需要知道电路在初始时间点的电压或电流值，这些值可以通过测量或已知条件来确定。

输入信号是指施加在电路上的信号。

输入信号可以是电压或电流的变化，它会引起电路的响应。

在分析一阶暂态电路时，我们需要知道输入信号的形式和参数，例如输入信号的幅值、频率和相位。

通过确定时间常数、初始条件和输入信号，我们可以使用一阶暂态电路三要素法来推导电路的暂态响应。

首先，我们可以根据时间常数来判断电路的响应速度。

如果时间常数很小，电路的响应会很快；如果时间常数很大，电路的响应会比较慢。

我们可以根据初始条件来确定电路的初始状态。

初始条件可以是电路的初始电压或电流值。

通过测量或已知条件，我们可以确定电路在初始时间点的初始条件。

我们可以根据输入信号的形式和参数来计算电路的暂态响应。

根据输入信号的幅值、频率和相位，我们可以计算出电路在不同时间点的电压或电流值。

总结一下，一阶暂态电路三要素法是一种用于分析一阶暂态电路响应的方法。

通过确定时间常数、初始条件和输入信号，我们可以推导出电路的暂态响应。

这种方法可以帮助我们更好地理解和分析一阶暂态电路的行为，对于工程实践中的电路设计和故障排除非常有用。

一阶电路三要素法的公式
一阶电路三要素法是一种对一阶电路进行分析的方法，它可以将一阶电路分解为三个简单元件：电阻、电感和电容。

其中，电阻是一种能够吸收运动电流，产生热量和电势差的元件；电感是一种在电路中存在的磁场，并能够存储能量的元件；而电容则可以在电路中存储电荷，具有调节电路的功能。

一阶电路三要素法的公式主要分为以下几个部分：
第一，电阻R：R=V/I，其中V为电压，I为电流。

第二，电感L：L=U/I，其中U为电势差，I为电流。

第三，电容C：C=Q/V，Q为电荷，V为电压。

第四，电路总模型：V=RI+L(dI/dt)+Q/C，其中V为电压，R为电阻，I为电流，L为电感，Q为电荷，C为电容。

第五，电路增益：A=Vout/Vin，Vout为输出电压，Vin为输入电压。

第六，电路阻抗：Z=V/I，V为电压，I为电流。

第七，电路时间常数：τ=L/R，L为电感，R为电阻。

以上就是一阶电路三要素法的公式，它可以用来分析一阶电路的不同特性，如电阻、电感、电容、增益、阻抗以及时间常数等。

要使用一阶电路三要素法，首先应该确定电路中所有组成元件的电压、电流和电荷。

然后，根据上述公式，依次计算电阻、电感、电容、增益、阻抗和时间常数，最终形成一个完整的一阶电路模型。

通过一阶电路三要素法，我们可以更好地理解电路，并给出有效的解决方案，可以大大提高工作的效率。

一阶电路分析的三要素法采用“三要素法”分析一阶电路，可以省去建立和求解微分方程的复杂过程，使电路分析更为方便和高效。

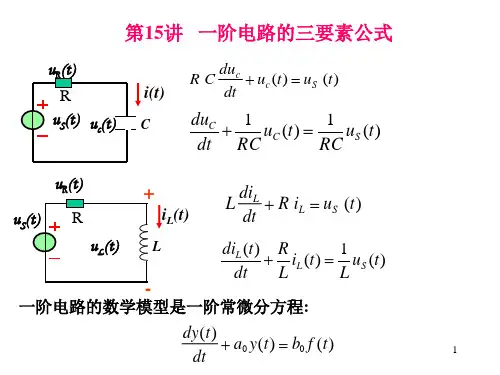
适用于直流激励一阶电路的三要素法我们仍以简单一阶RC 电路为出发点。

图1 所示RC 电路的全响应结果如下：图1 一阶RC电路图( 1 )( 2 )由图1 容易知道，电容电压的初值为，电容电压的终值为；而电流的初值为，电流的终值为。

观察式( 1 ) 、式(2) 可见，一阶电路中任意电路变量的全响应具有如下的统一形式：( 3 )可见，为求解一阶电路中任一电路变量的全响应，我们仅须知道三个要素：电路变量的初值、电路变量的终值以及一阶电路的时间常数。

我们称式( 6-5-3 ) 为一阶电路分析的三要素法。

三要素法同样适用于一阶RL 电路，但是二阶以上动态电路不可采用此法。

推广的三要素法在前面分析一阶电路时，我们采用的独立源具有共同的特点，即所有独立源均为直流（直流电压源或直流电流源）。

对于直流激励电路，换路前电路变量为稳定的直流量，换路后经历一个动态过程，电路变量过渡到另外一个稳定的直流量。

我们容易根据电路的原始状态和电路结构确定电路变量的初值f(0+)、电路变量的终值f(∞)以及一阶电路的时间常数。

如果电路中激励源不是直流，而是符合一定变化规律的交流量（如正弦交流信号），则换路后电路经历一个动态过程再次进入稳态，此时的稳态响应不再是直流形式，而依赖于激励源的信号形式（如正弦交流信号）。

此时，我们无法确定电路变量的终值f(∞),故无法采用式( 3 ) “三要素法”确定一阶电路全响应。

对于这类一阶电路，我们可以采用推广的三要素法：〔4 )式中，为全响应的初值、为电路的稳态响应、τ为电路的时间常数，称为一阶线性电路全响应的三要素，为全响应稳态解的初始值。

“三要素”的计算与应用利用三要素法分析一阶电路的全响应时，必须首先计算出电路变量的初值、电路变量的终值以及一阶电路的时间常数。

假设激励源为直流电压源或电流源。

三元素法分析一阶电路的全响应电路论文学院：电子信息工程学院班级：电气091502班姓名：***学号：************三元素法分析一阶电路的全响应摘要：本文主要介绍用三元素法分析解决一阶电路问题。

用三元素法求一阶电路问题首先要求出三元素：初始值，稳态值，时间常数，用三元素法可以直接代入公式求解，求解过程简单。

关键词：一阶电路 三元素法一、 全响应定义当一个非零初始状态的一阶电路受到激励时，电路的响应称为一阶电路全响应。

全响应总是由初始值、特解和时间常数三个要素决定的。

二、 三元素法的基本原理一阶电路的数学模型是一阶线性微分方程： 其解答一般形式为：令 t = 0+ 全响应f （t ）的三要素求解公式为f （t ）=f （∞）＋[f （0+）－f （∞）]e －t/τ其中，f （0+）为t=0+时刻的初始值，f （∞）为t →∞时的特解稳态值，τ为t ≥0时的时间常数。

f （0+）、f （∞）和τ称为三要素。

只要知道f （0+）、f （∞）和τ这三个要素，就可以根据上述公式直接写出直流激励下一阶电路的全响应，这种方法称为三要素法。

三、 三元素法的解题步骤⒈ 求初始值 ⑴ 初始值定义t=0+时电路中电压与电流的值称为初始值。

⑵ 初始值的求解① 由换路前电路（稳定状态）求u C (0－)和i L (0－)； ② 由换路定律得 u C (0+) 和 i L (0+)。

③ 画0+等效电路。

c bf tfa=+d d τteA t f t f -+'=)()(a.换路后的电路b.电容（电感）用电压源（电流源）替代。

（取0+时刻值，方向与原假定的电容电压、电感电流方向相同）。

④由0+电路求所需各变量的0+值。

⒉求稳态值⑴稳态值的定义t=∞时电路中电压与电流的值称为稳态值。

⑵稳态值的求解稳态时，电容C视为开路，电感L视为短路，稳态值即求直流电阻性电路中的电压和电源。

⒊求时间常数τ⑴时间常数τ的定义当电阻的单位为Ω，电容的单位为F时，乘积RC的单位为s，称为RC电路的时间常数，用τ表示。

实验三：一阶电路三要素法
一.实验内容及要求
1.使用Multisim仿真电路的全响应过程。

2.利用Multisim的虚拟仪器分析电路的全响应过程。

二.实验要求
1.掌握一阶电路的三要素法。

2.掌握Multisim仿真电路的全响应过程的方法。

三.实验设备
PC 机、Multisim 软件
四.实验步骤
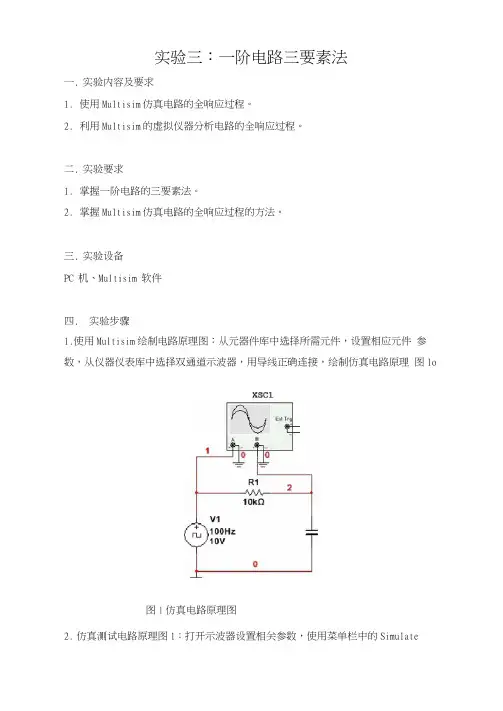
1.使用Multisim绘制电路原理图：从元器件库中选择所需元件，设置相应元件参数，从仪器仪表库中选择双通道示波器，用导线正确连接，绘制仿真电路原理图lo
图1仿真电路原理图
2.仿真测试电路原理图1：打开示波器设置相关参数，使用菜单栏中的Simulate
f Run命令进行仿真，使用菜单栏中的Simulate-Stop命令停止仿真，观察并记录示波器显示的波形。

波器显示的波形如下图：
3.改变仿真电路原理图1中电阻和电容的参数，使R1=1KQ,C1=1OMF,按照步骤2的方法，重新仿真测试电路，观察并记录示波器显示的波形。

仿真电路原理图2 波器显示的波形如下图:。

一阶电路的三要素法公式
其中：
- f(t)为电路中所求的响应（电压或电流）。

- f(0_+)为响应的初始值，即换路后瞬间t = 0_+时的值。

- f(∞)为响应的稳态值，即t→∞时的值。

- τ为一阶电路的时间常数，对于RC电路τ = RC，对于RL电路τ=(L)/(R)（这里R为从储能元件（电容C或电感L）两端看进去的戴维南等效电阻）。

在使用三要素法求解一阶电路时，一般按照以下步骤：
1. 求初始值f(0_+)：
- 首先根据换路前的电路（t = 0_-时的电路）求出储能元件（电容电压
u_C(0_-)或电感电流i_L(0_-)）的初始值。

- 然后根据换路定律（u_C(0_+) = u_C(0_-)，i_L(0_+)=i_L(0_-)）确定换路后瞬间电容电压和电感电流的值。

- 再根据换路后瞬间的电路（t = 0_+时的电路），利用电路的基本定律（如欧姆定律、基尔霍夫定律等）求出所求响应的初始值f(0_+)。

2. 求稳态值f(∞)：
- 画出换路后t→∞时的电路，此时电容相当于开路（i_C(∞)=0），电感相当于短路（u_L(∞)=0）。

- 利用电路的基本分析方法（如电阻的串并联化简、欧姆定律、基尔霍夫定律等）求出所求响应的稳态值f(∞)。

3. 求时间常数τ：
- 对于RC电路，τ = RC，其中R为从电容两端看进去的戴维南等效电阻。

- 对于RL电路，τ=(L)/(R)，其中R为从电感两端看进去的戴维南等效电阻。

最后将f(0_+)、f(∞)和τ代入三要素法公式f(t)=f(∞)+[f(0_+) - f(∞)]e^-(t)/(τ)中，即可求出一阶电路的响应f(t)。

一阶电路的三要素法
上式可写成：
在直流激励下，电路的任意一个全响应可用f(t)表示，则：
一阶电路暂态分析的三要素法
式中f(t)分代表一阶电路中任一电压、电流函数。

结论
依据三要素，可直接写出一阶电路在直流激励下的全响应，这种方法称为三要素法。

适用范围：激励为直流和正弦沟通。

三要素法求解暂态过程要点：
（1）分别求初始值、稳态值、时间常数；
（2）将以上结果代入暂态过程通用表达式；
（3）画出暂态过程曲线（由初始值→稳态值）。

（电压、电流随时间变化的关系）
1.初始值的计算
步骤: （1）求换路前的
（2）依据换路定则得出：
（3）依据换路后的等效电路，求其它的或
2.稳态值的计算
步骤:（1）画出换路后的等效电路（留意：在直流激励的状况下，稳态时令C开路，L短路）；
（2）依据电路的解题规律，求换路后所求未知数的稳态值。

注: 在沟通电源激励的状况下，要用相量法来求解。

求稳态值举例
3.时间常数的计算
原则:要由换路后的电路结构和参数计算。

(同一电路中各物理量的是一样的)
步骤:（1）对于只含一个R和C的简洁电路，对于较简单的一阶RC电路，将C以外的电路，视为有源二端网络，然后求其等效内阻R'。

则:
（2）对于只含一个L 的电路，将L 以外的电路，视为有源二端网络,然后求其等效内阻R'。

则:
RC 电路τ的计算举例
例9.
RL 电路τ 的计算举例
例10.
例11.
已知t = 0时合开关S，求换路后的uC(t)。

解：。

一阶电路三要素法公式
一阶电路三要素法公式是由美国物理学家威尔逊在1925年提出的，是用来计算一阶电路中电流、电压和功率的最基本的工程原理。

这个公式可以用来解决一般的一阶电路的基本问题，常用于生成各种信号的模拟电路。

一阶电路三要素法公式是：I=V/R，其中I代表电流，V代表电压，R代表电阻。

这个公式的意思是，在一个电路中，如果电压V和电阻R都是已知的，那么电流I就可以根据这个公式来计算出来。

而且，根据电路三要素法，电流I也可以用来计算电压V。

由于在电路中，当电流增加时，电阻会降低，这样电压V就会增加。

所以，根据三要素法，可以将电流I和电阻R代入公式，来计算出相应的电压V，即V=IR。

此外，还可以用三要素法来计算功率P。

在电路中，功率P是电流I和电压V之间的乘积，即P=IV。

所以，根据三要素法，将电流I和电压V代入公式，可以计算出相应的功率P，即P=IRV。

总之，电路三要素法公式是一种非常重要的工程原理，它可以用来计算一阶电路中的电流I、电压V和功率P。

它的公式是：I=V/R，V=IR，P=IRV，这些公式都是根据电路中电流、电压和功率之间的关系来推导出来的。