- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
令 直 线 y AB1 kx b ,则
y
解
4k
2
k
b b
1得 3
k
2,b
7
o
● B1 P●
x
y AB1
2x 7,令 y
0得 x
7 2
则 P ( 7 , 0 ), p 7
2
2
●B ●A
.
任务演练
变式二:(10年天津中考 25 )
在平面直角坐标系中,矩形 OACB的顶点O在坐标原点,
顶点A、B分别在x轴、y轴的正半轴上,OA 3,OB 4 ,
A●
P
m
B●
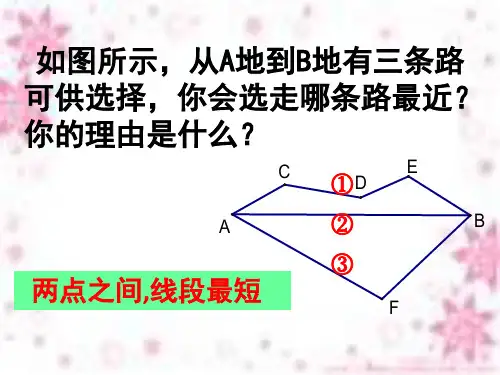
原理. :两点之间线段最短
学习任务一
如图,已知平面直角坐标系中,A、B 两
点的坐标分别为A (2,—3)B (4, 1),若点P
是x 轴上的一个动点,
则当P点坐标为
时,
y
AP+解B:P的B 点值关 最于 x小轴 的 对 称 点 B (1 4,1)
令 直 线 y AB1 kx b ,则
y
D为边OB的中点.
B
C
(1)若E为边OA上的一个动点,
当△CDE的周长最小时,
D
求点E的坐标;
O
Ax
E
.
任务演练 y
如图,作点D关于x轴的对称点 D , B
连接 C D 与x轴交于点E,即为所求。
由题意得C(3,4) D(0,2)
所以 D (0,-2) 设直线CD 为y=kx+b 则
(0,2)
2、直线y=kx+b过点A(2,-3)和点
任务要求: B(4,1),则这条直线解析7 式为:y=2x-7 .
它与x轴交点坐标为 ( 2 ,0)
,与y轴
交点坐标自为主(0,独-7) 立完成
3、直线y=x和直线y=
的交点
坐标为 (2,2)
.
学习任务一
小明家住在B地,小明带着牛在A地吃完草后 到小溪m中饮水,然后再回家,请问小明带 着牛到小溪m的什么地方喝水能使所走的路 径最短?
别为A (2,—3)B (4,—1),若点P是x 轴上的一个动点,
则当P点坐标为
时,AP+BP的值最小
解 : BA点 关 于 x 轴 的 对 称 点 BA(11(4,12),3)
令 直 线 y AAB1B1 k x b , 则
● A1 y
解
42kk+ bb=3 24kk+bb=-1
1
3
得
kk=-22 ,,bb=7
7
o
P● x
y A AB11B
2-2x x+77 , 令 y
0得 x
7 2
则 P ( 7 , 0 ), p 7
2
2
●B ●A
.
最短路径问题
如图,已知平Байду номын сангаас直角坐标系中,A、B 两点的坐标分
别为A (2,—3)B (4,—1),若点P是x 轴上的一个动点,
则当P点坐标为
时,AP+BP的值最小
解 : B 点 关 于 x 轴 的 对 称 点 B (1 4,1)
B●
A●
B
A
P●
l
l
●A′
AP+BP最短
原理. :两点之间线段最短
学习任务二
变式一:如图,已知平面直角坐标系中,A、 B 两点的坐标分别为A (2,—3)
B (4,—1),若点P是x 轴
y
任务要求: 上的一个动点,则当P点坐
标为
时,
自主独立完成 AP+BP的值最小
x
●
B
●
A
.
最短路径问题
如图,已知平面直角坐标系中,A、B 两点的坐标分
D
3k+b=4 解得 k=2
b=-2
b=-2
所以直线CD 解析式为y=2x-2
O E
当y=0时 x=1 所以E(1,0)
D
(0,-2)
.
C (3,4)
Ax
任务演练
变式三:如图,平面直角坐标系中有正方形
OABC,B(6,6), D为OC中点,在直线OB:y=x 上有一动点P,当P点坐标
为
时,
△CDP周长最小。
.
任务演练
因为四边形OABC为正方形,OB为对角线,连接AC, AC与OB互相垂直平分,所以C点关于直线OB的对称
点为A点。连接AD交OB于点P,即为所求。
由题意得A(6,0) D(0,3)
设直线AD为y=kx+b 则 6k+b=0 解得 k=
1 2
b=3
b=3
所以直线AD解析式为y=
1
2 x+3
P
Q
B/
A
M
B
l
三条线段AP+PQ+QB的和. 最小
学习任务三
变式四:如图,已知平面直角坐标系中,A、 B两点的坐标分别为A(2,—3)B(4,—1),
设点P、Q分别为x轴和y轴上的动点,
P(p,0),Q(0,q),四边形
APQB周长最小时
p=
,q=
.
.
学习任务三
作点A(2,-3)关于y轴对称点A'(-2,-3),点B(4,-1)关于 x轴对称点B'(4,1),连接A'B',分别交x轴y轴于点P和 点Q,即为所求。
y=
1 2
x+3
解得
x=2
P
y=x
y=2
所以P(2,2)
.
任务演练
变式三:如图,平面直角坐标系中有正方形
OABC,B(6,6), D为OC中点,在直线OB:y=x上
有一动点P,当P点坐标
为由设题直最6b意线k=小+得A3bD周A=为(0时6y长,0解=,)k为得xD△+(b0多C,3则bkD=)=少P3 周12?长最小。
所以直线AD解析式为y= 1 x+3
CD3
y=
1 2
x+3 解得
x=22
P
ADy=xAO2OD2 6y2=232 3 5
最 所小 以周 P(长 2,2为) : 3+3 5
.
学习任务三
小明带着牛在A处,打算带着牛先去吃草,然 后到河边喝水,再回家,请问这次小明带着牛
怎样走能使所走路径最短?
N
A/
一次函数之 最短路径问题
.
任务目标
• 1、能用一次函数的知识解决最短 路径问题,体会数形结合思想。
• 2、能够从复杂问题中抽象出“最 短路径”的基本数学模型。
• 3、提高数学建模能力,感受数学 学习乐趣。
.
一次函数之 最短路径问题
.
知识储备任务
1、点M (4,-1)关于x轴对称点的坐标
为 (4,1) ,关于y轴对称点的坐标为(-4,-1.)
设直线A'B'解析式为y=kx+b 则
-2k+b=-3 解得 k 2
4k+b=1
3
b 5
3
直线A'B'解析式为:y 2 x 5
33
P
当 x0 时 , y5,所 以 q5
Q
3
3
当 y0 时 , x5 2,所 以 p . 5 2(-2A,' -3)
B' (4,1)
任务小结
A 这节课除了又巩固
1、 了P 这些最e 短路3、 径的
解
4k
2
k
b b
1得 3
k
2,b
7
(4,1)
●
B
P
x
y AB1
2x
7,令 y
0得 x
7 2
●
A(2,-3)
则 P ( 7 , 0 ), p 7
2
2
.
学习任务二
小明家搬到了小溪对面的B处,他带着牛在A 处吃完草后先到小溪喝水,再回家,请问这 次小明带着牛到小溪l的什么地方喝水能使所 走路径最短?