(苏教版)数学六上《长方体与正方体》练习

第一单元长方体和正方体注意事项：1.答题前填写好自己的姓名、班级、考号等信息。

2.请将答案正确填写在答题卡上。

3.答完试卷后。

务必再次检查哦！一、选择题（18分）A．4B．5C．6D．78．用3个棱长为2分米的正方体拼成一个大长方体，这个长方体的表面积是（）平方分米。

A．72B．64C．56D．60二、填空题（12分）13．把两块长4三、判断题（12分）四、计算题（12分）24．直接写得数．0.25＋2.7＝0.8×1.25＝0.33＝0.23＝8.1÷0.09＝0.13＝25．解方程．6.4x－x＝32.48×2.5－3x＝10.4五、图形计算（12分）26．求下图的表面积（单位：cm）。

27．计算长方体、正方体涂色面的面积．28．如图分别是一个长方体的前面和右面（单位：分米），那么这个长方体的底面积是多少？六、解答题（36分）29．如图所示用绳子捆扎一种礼品盒，如果结头处的绳长为12厘米，一根10米长的绳子最多可以捆几盒？还剩多少厘米？30．仓库里有以下4种规格的长方形、正方形铁皮若干张．(单位:分米)从中选出5张铁皮,焊接成一个无盖的长方体或正方体水箱,要使水箱的容积最大,可以怎样选?焊接成的水箱的容积是多少?(铁皮厚度忽略不计)31．(思维训练题)用一根绳子捆扎礼盒(如图),如果接头处的绳子长30 cm,求这根绳子的长度．32．下面是一个长方体包装盒的展开图，请你计算出它的底面积和体积。

（单位：厘米）33．一个游泳池长50米，宽30米，深2米。

（1）这个游泳池的占地面积是多少？（2）要在游泳池的各个面上抹一层水泥，抹水泥的面积是多少平方米？（3）如果每平方米要抹水泥12千克，那么22吨水泥够用吗？34．如图把一个长20厘米，宽15厘米，高18厘米的礼品盒包扎起来，问，至少需要包扎带多少厘米？（打节处每处长8厘米）参考答案：1．B2．C【分析】石块占据的是原来溢出的水的空间，二者体积相等。

长方体和正方体测试卷一、选择题（题型注释）米，宽和厚都是2分米，把它锯成4段，表面积增加( )平方分米。

A. 8B. 16C. 24D. 322.把一个长方体分成几个小长方体后,体积( ),表面积( )。

A. 不变 B. 比原来大了 C. 比原来小了3.用一根长（ ）铁丝正好可以做一个长6厘米、宽5厘米、高3厘米的长方体框架。

A. 28厘米B. 126平方厘米C. 56厘米D. 90立方厘米4.一个正方体的棱长总和是60厘米，它的表面积是（ ）。

A. 21600平方厘米B. 150平方厘米C. 125立方厘米5.将下图沿虚线折起来，可折成一个正方体。

这时正方体的5号面所对的面是( )号面。

A. 2B. 3C. 4D.6二、填空题（题型注释）长方体（或正方体）有 个顶点，有 条棱，有 个面．7.一个正方体的棱长是8分米，它的棱长总和是（_____）分米，表面积是（_____）平方厘米，体积是（_____）立方分米。

长方体的长为7cm ，宽为5cm ，高为3cm ，它的棱长总和是（_____）厘米；表面积是（_____）平方厘米；体积是（_____）立方厘米8.一个长方体的底面积是80平方厘米，高是7厘米，它的体积是 立方厘米．9.一个长方体的金鱼缸，长是8分米，宽是5分米，高是6分米，不小心前面的玻璃被打坏了，修理时配上的玻璃的面积是 平方分米．10.500cm 3 = （_____）dm 3= （_____）L 750000cm 3= （_____）dm 3= （_____）m 311.一根长方体的方木，横截面的面积为25平方厘米，长5分米，它的体积是（_____）平方厘米。

12.把30L 水装入容积是250ml 的水瓶里，能装 瓶．13.至少要 个小正方体才能拼成一个大正方体，如果一个小正方体的棱长是5厘米，那么大正方体的表面积是 平方厘米，体积是 立方厘米．14.物体所占 的大小叫做物体的体积；容器所能容纳物体的体积，叫做容器的 ．15.长方体的面中不可能有正方形． ．16.一个正方体的棱长总和是72 cm ，它的表面积是（____），体积是（_____）。

长方体和正方体第1课时一、填空题。

1．长方体有个顶点，有条棱，有个面，一般情况下面的面积相等。

正方体是的长方体。

2．一个正方体的棱长是8分米，它的棱长总和是分米。

3. 我们在画长方体时一般只画出三个面，这是因为长方体最多看到个面。

4. 用一根长铁丝正好做一个长6厘米、宽5厘米、高3厘米的长方体框架。

5. 一个长方体长6厘米、宽2厘米、高1.5厘米，它的棱长总和是。

6.用36厘米的铁丝折一个正方体框架，这个正方体棱长是。

7. 一个长方体的棱长总和是48厘米，长是5厘米，宽是4厘米，它的高是。

8.一个正方体的棱长是4米，它的棱长总和是，每个面的面积是。

9.一根80分米长的铁条，剪断后刚好可焊接成一个长8分米，宽5.5分米的长方体框架。

这个长方体的高是分米。

二、判断题（对的打“√”，错的打“×”）。

1．所有的长方体都有六个面。

………………………………（）2．长方体中对面的面积是相等的。

…………………………（）3．长方体的表面中不可能有正方形。

………………………（）4．正方体的表面中有可能有长方形。

………………………（）5．长方体的六个面中有可能有四个面的面积相等。

………（）三、解决实际问题。

1.用三个棱长2分米的正方体拼成一个长方体，这个长方体的棱长总和是多少分米？2.一根铁丝长84厘米，围成长方体相交于一个顶点的两条棱长为15厘米、4厘米，那么这个顶点的第三条棱长为多少厘米？这个长方体的前面面积是多少平方厘米？3.一个长方体长、宽、高为三个连续的自然数，且他们的和是24，这个长方体的棱长总和是多少？4.王师傅有2根一样长的铁丝，一根围成了长8分米、宽6分米、高为4分米的长方体框架，另一根围成另一个正方体框架。

这个正方体框架的棱长是多少？30 10 6 长方体和正方体第2课时1.下面哪些图形折叠后能围成正方体？ （能围成正方体的画“√”，不能围成正方体的画“×”）（ ） （ ） （ ） （ ） （ ） （ ）2.下面哪些图形沿虚线折叠后能围成一个长方体？（能围成长方体的画“√”，不能围成长方体的画“×”）（ ） （ ） （ ） （ ） （ ） （ ）3.如图，是一个正方体的展开图，其中与1号面相对的是（ ）号面，与2与2号面相对的是（ ）号面，与3号面相对的是（ ）号面。

六上《长方体和正方体》专项练习（一）题型一：长方体展开图求面积解法点拨：步骤1.确定“前面”，2.描出长、宽、高（三条交于一点），3.找出已知长度再求其余长度。

例1：一个长方体的平面展开图如右图所示（长度：dm），求它的表面积和体积。

【反馈练习】1.一个长方体的平面展开图如右图所示（长度：c m），求它的表面积。

2. 一个长方体的平面展开图如右图所示（长度：c m），求它的表面积。

★3.右图是一个无盖长方体纸盒的展开图，请算出这个长方体纸盒的表面积和体积。

题型二：长方体和正方体展开图的判断解法点拨：1.正方体：“141”“231”“222”“33”四种模型共11种。

2.长方体：符合正方体的基础模型，同时根据对应面相等（一个隔一个）判断。

例2：下面图形中，能沿虚线折成正方体的是（）。

例3：下面的图形沿虚线折叠，哪些能折成一个长方体？在括号里画“√”，不能的画“×”。

【反馈练习】1. 下面的图形沿虚线折叠，哪些能折成一个长方体？在括号里画“√”，不能的画“×”。

2.下面是一个正方体的展开图，将它折叠成正方体后，与数字6相对的数字是（）。

A. 1B. 2C. 3D. 4★3.下面这个正方体的展开图可能是（）。

★4.下面是同一个正方形从三个不同角度拍到的照片，这个正方体的展开图是（）。

六上《长方体和正方体》专项练习（二）题型一：表面积和体积扩大倍数问题解法点拨：看“单位即可”，棱长（单位：m）扩大a倍，则棱长和（单位：m）扩大a倍,表面积（单位：m2）扩大a2倍，体积（单位：m3）扩大a3倍。

例1：一个正方体的棱长扩大为原来的2倍，则棱长和扩大为原来的（）倍，底面积扩大为原来的（）倍，表面积扩大为原来的（）倍，体积扩大为原来的（）倍。

A . 2 B. 4 C. 12 D. 8【反馈练习】1.一个正方体的棱长扩大为原来的3倍，则棱长和扩大为原来的（）倍，底面积扩大为原来的（）倍，表面积扩大为原来的（）倍，体积扩大为原来的（）倍。

苏教版小学数学六年级上册单元测试题姓名 -------- 班级 --------- 分数 ---------一、填空1、有一个长方体长、宽、高分别是7 厘米、 5 厘米、 3 厘米，它的棱长之和是（）2、做一个长方体框架，长8 厘米，宽 5 厘米，高 4 厘米，要用（）厘米的铁丝，这是求长方体的（）；假如在框架表面上贴上塑料板，要用（）平方厘米的塑料板，这是求长方体的（），这个长方体占空间（）立方厘米，这是求长方体的（）。

3、 0.7 立方米 =（）立方米（）立方分米4、一个长方体的体积是96 立方分米，底面积是16 立方分米，它的高是（）分米。

5、有一长方体木材长 3 厘米，宽 3 厘米，高 2 厘米。

把他切成 1 立方厘米的小方块能够切成（）块。

6、用一根 12 分米长的铁丝围成一个最大的正方体形状的框架，这个正方体得体积是（）立方分米。

7、一个正方体的棱长总和是108 分米，这个正方体的表面积是（）平方分米，体积是（）立方分米。

8、一个正方体的表面积是72 平方分米，占地面积是（）平方分米。

9、有一个正方体，棱长 3 厘米。

若将每条棱长扩大 2 倍，这个正方体的体积应是（），表面积应是（）。

10、用3个棱长4分米的正方体粘合成一个长方体，长方体的表面积比3 个正方体的表面积少（）平方分米。

二、判断题。

1、只有 6 个面都是长方体的物体才叫长方体。

2、长方体中的三条棱长分别叫做长、宽、高。

3、求一个容器的容积，就是求这个容器的体积。

4、一个正方体的棱长之和是12 厘米，体积是 1 立方厘米。

5、一个正方体的棱长是a，因此这个正方体的体积是3a.6、长方体的体积都比正方体的体积大。

7、把 2 块棱长都为 2 厘米的正方体拼成一个长方体，表面积增添了8 平方厘米。

8、由于用 2 个相同大小的正方体拼成的长方体的体积扩大 2 倍，因此表面积也扩大到本来的 2 倍。

9、假如两个长方体的体积相等，它们的长、宽和高的长度一定相等。

（苏教版）六年级数学上册《长方体与正方体》练习（一）班级_______姓名_______分数_______一、填空1.长方体或者正方体（）叫做它的表面积。

2.一个正方体的棱长是10厘米，它的表面积是（）平方厘米。

3.一个长方体长4分米，宽3分米，高2分米，它的表面积是（）平方分米。

4.正方体的棱长之和是60分米，它的表面积是（）平方分米。

5.用两个长6厘米，宽3厘米，高1厘米的长方体拼成一个表面积尽可能小的正方体，这个拼成的长方体的表面积是（）平方厘米。

二、选择题。

1.用两个棱长是1分米的正方体小木块拼成一个长方体，拼成的长方体的表面积是（）。

A.增加了B.减少了C.没有变2.如果把一个棱长是10厘米的正方体切成两个完全相同的长方体，这两个长方体的表面积之和比原来的正方体表面积（）。

A.增加了B.减少了C.没有变化3.正方体的棱长扩大2倍，它的表面积就（）。

A.扩大2倍B.扩大4倍C.扩大6倍4.大正方体的表面积是小正方体的4倍，那么大正方体的棱长之和是小正方体的（）A.2倍B.4倍C.6倍D.8倍5.把一个正方体切成大小相等的8个小正方体，8个小正方体的表面积之和（）。

A.等于大正方体的表面积B.等于大正方体表面积的2倍C.等于大正方体表面积的3倍三、一个房间长5米，宽3米，高2.8米，现需油漆四壁和天花板，扣除门窗的面积4.5平方米，求油漆的总面积有多大？四、要做一种管口周长40厘米的通气管子10根，管子长2米，至少需要铁皮多少平方米？五、一个正方体的表面积是54平方分米，这个正方体所有棱长之和是多少？六、有一个长方体木箱，长0.7米，宽0.5米，高0.3米。

怎样放，这个木箱占地面积最小？最小是多少平方米？薄雾浓云愁永昼，瑞脑消金兽。

佳节又重阳，玉枕纱厨，半夜凉初透。

东篱把酒黄昏后，有暗香盈袖。

莫道不消魂，帘卷西风，人比黄花瘦。

苏教版小学数学六年级上册《长方体与正方体》专项练习试题（10套）（1）（长方体和正方体的认识）一、填空：（38%）1、长方体和正方体都有( ) 个面，( ) 条棱，( ) 个顶点。

2、长方体的每个面都是( )形或有一组对面是( )。

它有( )条棱，平行的( )条棱都相等。

3、相交于长方体一个顶点的三条棱的长度分别叫做它的（）、（）和（）。

4、长方体有（）个面，从不同的角度观察一个长方体，最多能看到（）个面。

5、一个长方体的长是5分米，宽是4分米，高是3分米，6个面中最小的一个面的面积是（），最大的一个面的面积是（）。

6、一个长方体，长4米，宽3米，高2米，它的占地面积最大是（）平方米。

7、一个长方体模型，从前面看是从上面看是长方体右面的面积是（）平方厘米。

8、长方体的右侧面面积是12平方厘米，前面面积是8平方厘米，上面面积是6平方厘米，这个长方体的长、宽、高分别是（）、（）、（）。

二、选择（8%）：1、一个长方体水池，长20米，宽10米，深2米，这个水池占地（）平方米。

A、200B、400C、5202、下面的图形中，能按虚线折成正方体的是（）。

3、从一个体积是30立方厘米的长方体木块中，挖掉一小块后(如下图) ，它的表面积( ) 。

A．和原来同样大 B．比原来小 C．比原来大 D．无法判断4、用一根52厘米长的铅丝，正好可以焊成长6厘米，宽4厘米，高（）厘米的长方体教具。

A、2B、3C、4D、5三、计算下面每个形体的棱长和（6%）。

四、下面各题，列式计算，不写答。

（40%）1、一个长方体，长5分米，宽3分米，高4分米，求它的所有棱长的和。

2、用钢筋做一个长和宽都是3.5分米，高是10厘米的长方体，需多少分米的钢筋？3、棱长是4分米的正方体，棱长总和是多少分米？4、一个长方体的棱长和是36厘米，从一个顶点出发的三条棱的长度总和是多少厘米？5、同一根长96厘米的铁丝折成一个最大的正方体框架，求正方体框架的棱长。

小学数学苏教版六年级上册第一单元《长方体和正方体》测试卷一．选择题1．观察如图，与字母B和字母F相对的面分别是（ ）A．C．D B．A．E C．D．E D．A．E2．一个长方体的体积是100立方厘米，已知它的长是10厘米，宽是2厘米，则高是（ ）厘米．A．3B．4C．5D．63．一个长26厘米，宽19厘米，高7毫米的长方体物体，最有可能是（ ）A．橡皮B．冰箱C．数学书D．普通手机4．一个长方体挖掉一个小正方体（如图），下面说法正确的是（ ）A．体积减少，表面积减少B．体积减少，表面积增加C．体积减少，表面积不变D．体积不变，表面积不变5．如图中，甲的表面积（ ）乙的表面积．A．大于B．小于C．等于D．不能确定二．填空题1．如图是一个长方体的展开图．原来这个长方体的底面积是 平方厘米，体积是 立方厘米．2．如图是一个未做完的长方体框架．①做一个完整的长方体框架，至少需要铁丝 厘米；②如果在完整的框架外面糊上一层纸板，至少需要 平方厘米纸板．3．棱长2米的正方体里面可以装 个棱长2分米的正方体．4．有9根a厘米长和6根b厘米长的小棒，用其中的12根搭成长方体框架，长方体框架的棱长总和为 厘米．5．把2个棱长是1cm的正方体拼成一个长方体，这个长方体的表面积是 ，体积是 ．6．长方体和正方体都有 个面， 个顶点， 条棱．7．一个长方体的体积是150立方分米，宽和高都是5分米，这个长方体的长是 分米，表面积是 平方分米．8．一个正方体棱长5dm，这个正方体棱长之和是 dm，它的表面积是 dm2，它的体积是 dm3．9．一根3米长的方钢，把它横截成3段时，表面积增加80平方厘米，原来方钢的体积是 ．三．计算题1．求下列长方体的体积和表面积（1）棱长6厘米的正方体（2）长4厘米，宽2厘米，高3厘米2．求这个物体的表面积（单位：厘米）3．计算下面长方体的表面积和体积．四．应用题1．用一根4.8m长的铁丝正好围成一个正方体，这个正方体的体积是多少立方分米？2．一个玻璃鱼缸的形状是正方体，棱长5分米．（1）制作这个鱼缸时至少需要玻璃多少平方分米？（上面没有盖．）（2）爸爸在这个鱼缸里放了一个假山石，水面上升了4厘米．这个假山石的体积有多大？3．一种长方体铁皮通风管长3m，管口是边长2dm的正方形．王师傅做一节这样的通风管，至少需要多少平方米的铁皮？（接口忽略不计）4．从里面量一种汽车油箱长8dm，宽3dm，高2.5dm．（1）这个油箱最多能装多少升汽油？（2）如果一辆汽车每千米的耗油量是0.08L，这箱油最多可以供汽车行驶多少千米？5．做一个长方体形状的金鱼缸（无盖），长8分米、宽4分米、高6分米，至少需要多少平方分米的玻璃？如果每平方分米的玻璃需要4元，那么至少需要多少元买玻璃？6.一个正方体包装盒，棱长4.5分米，底面是木板，四周和上面用的是硬纸板。

第一单元长方体和正方体测试卷附答案姓名：成绩：一、填空题（每空1分，共20分）1、230cm3=（）ml0.6dm3=（）L=（）ml6800ml=（）L0.45m3=（）dm32500cm2=（）m215m26dm2=（）m2240立方厘米=（）立方分米34.8立方米=（）立方分米2.08立方分米=（）升（）毫升2、一个长方体长5cm，宽4cm，高2cm，这个长方体上面的面积是（）cm2，前面的面积是（）cm2，右面的面积是（）cm2，它的表面积是（）cm2，体积是（）cm3。

3、挖一个容积为48m3的长方体土坑，占地面积为24m2，这个土坑深（）m。

4、40升水倒入长0.4米，宽0.2米的玻璃缸中，水深（）分米。

5、正方体的棱长扩大3倍，棱长和扩大（）倍，表面积扩大（）倍，体积扩大（）倍。

二、选择题（每题2分，共10分）6、边长是6分米的正方体，它的表面积与体积比较（）。

A．一样大B．表面积大C．不好比较大小D．体积大7、下面能折成正方体的是（）。

A. B. C. D.8、一个长6dm，宽4dm，高5dm的长方体盒子，最多能放（）个棱长为2dm的正方体木块。

A.12B.13C.14D.159、靠着墙边摆放着一个由小正方块堆成的正方体，露在外面的可能面有（）个。

A．13B．27C．17D．1910、把一个棱长3分米的正方体切成两个相等的长方体，表面积增加了（）平方分米。

A．18B．9C．36D．以上答案都不对三、判断题（对的打“√”，错的打“×”。

每题2分，共10分）11、表面积相等的两个长方体，它们的体积一定相等。

……………………………………（）12、一个冰箱的体积大于它的容积。

…………………………………………………………（）13、把表面积6cm2的两个正方体拼成一个长方体，长方体的表面积是12cm2。

………（）14、长方体的六个面中有可能有四个面的面积相等。

……………………………………（）15、体积相等的两个正方体，它们的表面积一定相等。

（1）表面积的求解（要点察看需要几个面）长方体水槽，无盖的鱼缸，火柴盒的外壳，通风管，名著的书套，楼梯，广告周围包装，涂周围墙壁（加顶部）谈谈上边的面数状况？课外增补：叙述底面积，横截面，侧面积的意思？思虑与体积的关系？例题（1）有一个长方体纸盒，量得它的长、宽、高分别是16 厘米、 8 厘米、 12 厘米。

问题 1：做这个纸盒起码用了多少平方厘米纸板？第一察看有几个面，有哪些面？问题 2：假如盒子不带盖，如何计算它的纸板用料。

问题 3：假如在它的周围贴上一层商标纸，如何计算商标纸的面积？讲堂训练1.一间教室的长是 8 米, 宽是 6 米, 高是 4 米, 要粉刷教室的四壁和顶面 , 除掉门窗和黑板面积 24 平方米 , 粉刷的面积是多少平方米 ?2.学校活动中心要油漆 5 根柱子，柱子横截面是边长 3 分米的正方形，每根柱子高 4 米，每平方米油漆 5 元，买油漆共要多少元？（ 2）表面积的增添与减少问题（‘切一刀’‘抱一同’）例题 1 一个棱长是 8 厘米的正方体，将它切成两个完整同样的长方体，请问它们的表面积的变化？变化多少？（‘切一刀’）变式题 1：假如此刻换成一个长是 14 厘米，宽是 5 厘米，高是 7 厘米的长方体，假如我给他一刀，你会如何切，分别求出一刀后，增添（或减小）的表面积？思虑：假如我们切两刀或更多呢？会有什么发现？变式题 2: 请问假如要使增添表面积最大，怎么切？要使增添的表面积最小，怎么切？例题2有3个棱长是 3 厘米的小正方体拼成一个长方体，表面积减少（）平方厘米。

（‘抱一同’）在我们练习中间也会碰到这两种种类以外的题，以下所示：课外增补：一个长方体的底面是一个边长为30cm 的正方形，高为40cm，假如把它的高增添 5cm，它的表面积会增添（）。

（还有表面涂色问题，用容器算体积的问题，我们下一节课持续讲！感谢）（ 3）容器体积的计算公式：放入（取出）物体的体积=上涨（降落）的高度×容器的底面积1. 把一个棱长 10 厘米的正方体铁块放入一个长 50 厘米、宽 40 厘米、高 30 厘米的玻璃缸中 , 本来缸中水深 20 厘米 , 此刻水面高升几厘米 ?变试题：（1）一个不规则的铁块，放入一个长 50 厘米、宽 40 厘米、高 30 厘米的玻璃缸中，水面上涨了 2 厘米，请问铁块的体积是多少？（2) 一个规则的铁块和一个不规则的铁块，放入一个装满水的容器中，规则的铁块放入，水面上涨 4 厘米，而不规则的则上涨了 12 厘米，请问不规则的铁块体积是规则的多少倍？典型训练1.在一个长为 25 厘米、宽为 20 厘米的玻璃缸中，有一块棱长为 20 厘米的正方体铁块，这时水深 22 厘米，假如把这块铁块从缸中取出来，那么缸中的水深多少厘米？一个不规则的铁块是正方体铁块的 5 倍，请问放进去水面会上涨多少厘米？。

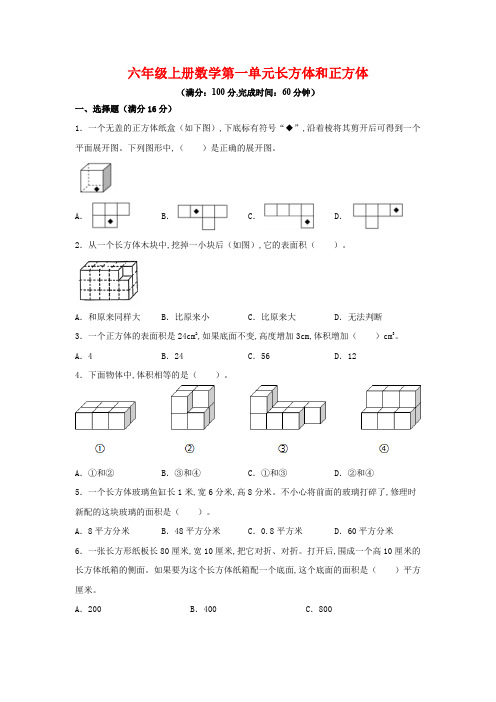
六年级上册数学第一单元长方体和正方体（满分：100分,完成时间：60分钟）一、选择题（满分16分）1．一个无盖的正方体纸盒（如下图）,下底标有符号“◆”,沿着棱将其剪开后可得到一个平面展开图。

下列图形中,（）是正确的展开图。

A．B．C．D．2．从一个长方体木块中,挖掉一小块后（如图）,它的表面积（）。

A．和原来同样大B．比原来小C．比原来大D．无法判断3．一个正方体的表面积是24cm2,如果底面不变,高度增加3cm,体积增加（）cm3。

A．4 B．24 C．56 D．124．下面物体中,体积相等的是（）。

A．①和②B．③和④C．①和③D．②和④5．一个长方体玻璃鱼缸长1米,宽6分米,高8分米。

不小心将前面的玻璃打碎了,修理时新配的这块玻璃的面积是（）。

A．8平方分米B．48平方分米C．0.8平方米D．60平方分米6．一张长方形纸板长80厘米,宽10厘米,把它对折、对折。

打开后,围成一个高10厘米的长方体纸箱的侧面。

如果要为这个长方体纸箱配一个底面,这个底面的面积是（）平方厘米。

A．200 B．400 C．8007．如果有5根8厘米、10根10厘米的小棒,用其中的12根搭一个长方体,那么长方体的棱长总和为（）厘米。

A．110 B．112 C．140 D．928．大厅里有4根4米高的长方体柱子,底面均为边长为4分米的正方形。

浇筑这些柱子需要（）立方米的混凝土,若给柱子的表面贴上瓷砖,则每根柱子贴瓷砖的面积是（）平方米。

A．0.64,0.64 B．2.56,6.4 C．0.64,2.56 D．0.64,25.6二、填空题（满分16分）9．用60厘米长的铁丝正好做成一个正方体框架（接头处忽略不计）,这个正方体的棱长是( )厘米,如果在它的表面糊上一层纸,至少需要( )平方厘米的纸,这个正方体的体积是( )立方厘米。

10．焊接一个正方体框架,一共用去铁丝60厘米,这个正方体框架的棱长是( )厘米（接头处忽略不计）,如果用彩纸贴满正方体的各个面。

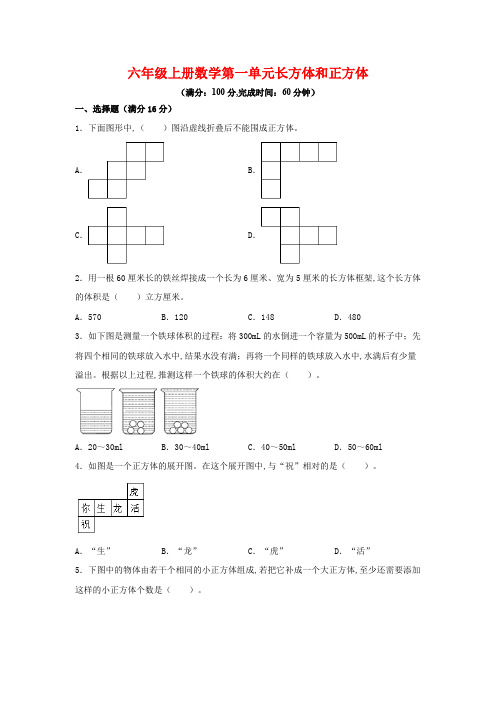
六年级上册数学第一单元长方体和正方体（满分：100分,完成时间：60分钟）一、选择题（满分16分）1．下面图形中,（）图沿虚线折叠后不能围成正方体。

A．B．C．D．2．用一根60厘米长的铁丝焊接成一个长为6厘米、宽为5厘米的长方体框架,这个长方体的体积是（）立方厘米。

A．570 B．120 C．148 D．4803．如下图是测量一个铁球体积的过程：将300mL的水倒进一个容量为500mL的杯子中；先将四个相同的铁球放入水中,结果水没有满；再将一个同样的铁球放入水中,水满后有少量溢出。

根据以上过程,推测这样一个铁球的体积大约在（）。

A．20～30ml B．30～40ml C．40～50ml D．50～60ml4．如图是一个正方体的展开图。

在这个展开图中,与“祝”相对的是（）。

A．“生”B．“龙”C．“虎”D．“活”5．下图中的物体由若干个相同的小正方体组成,若把它补成一个大正方体,至少还需要添加这样的小正方体个数是（）。

A．9 B．14 C．166．一个长方体的游泳池,长20米,宽6米,深2米,现在绕池口走一圈要走（）米。

A．44 B．344 C．52 D．2407．一盒有净含量为600毫升的长方体盒装酸奶,量得外包装长8厘米,宽5厘米,高15厘米,根据以上数据,你认为净含量的标准是（）。

A．真实B．虚假C．无法确定8．12个棱长1厘米的小正方体拼成长方体,一共（）种拼法。

A．3 B．4 C．5 D．6二、填空题（满分16分）9．0.3m2＝( )dm24060毫升＝( )升2时40分＝( )时10．在括号里填上合适的数。

32吨＝( )吨( )千克3时45分＝( )时5250公顷＝( )平方千米180毫升＝( )立方分米11．一个正方体,棱长总和是6分米,这个正方体的体积是( )立方分米。

12．一个长方体的长、宽、高分别是6分米、5分米、4分米,那么它的棱长总和是( )分米,体积是( )立方分米。

苏教版小学数学六年级上册《长方体与正方体》)练习题(1）（长方体和正方体的认识）一、填空：1、长方体和正方体都有( ) 个面，（）条棱，（ ) 个顶点。

2、长方体的每个面都是（ )形或有一组对面是（ ). 它有（）条棱,平行的（ )条棱都相等。

3、相交于长方体一个顶点的三条棱的长度分别叫做它的（）、（）和（）。

4、长方体有( ）个面,从不同的角度观察一个长方体，最多能看到（）个面.5、一个长方体的长是5分米，宽是4分米，高是3分米，6个面中最小的一个面的面积是（）,最大的一个面的面积是（）。

6、一个长方体，长4米，宽3米,高2米，它的占地面积最大是（ )平方米.7，长方体的右侧面面积是12平方厘米，前面面积是8平方厘米,上面面积是6平方厘米，这个长方体的长、宽、高分别是（）、( ）、（ )。

二、选择：1、一个长方体水池，长20米，宽10米，深2米，这个水池占地（）平方米。

A、200B、400C、5202、下面的图形中，能按虚线折成正方体的是（）.3、从一个体积是30立方厘米的长方体木块中，挖掉一小块后(如下图) ，它的表面积( ) .A．和原来同样大 B．比原来小 C．比原来大D．无法判断4、用一根52厘米长的铅丝，正好可以焊成长6厘米，宽4厘米，高（ )厘米的长方体教具。

A、2B、3C、4D、5三、计算下面每个图形的棱长和。

1、一个长方体,长5分米,宽3分米，高4分米，求它的所有棱长的和.2、用钢筋做一个长和宽都是3。

5分米,高是10厘米的长方体，需多少分米的钢筋？3、棱长是4分米的正方体，棱长和是多少分米?4、一个长方体的棱长和是36厘米，从一个顶点出发的三条棱的和是多少厘米?5、同一根长96厘米的铁丝折成一个最大的正方体框架，求正方体框架的棱长。

6、一个长方体的长是15厘米,宽是12厘米,棱长总和是148厘米，求它的高。

7、两根同样长的铁丝焊一个长方体和正方体，长方体长7厘米,宽5厘米，高3厘米,求正方体的棱长.8、一根铁丝，如果做成一个正方体框架模型，棱长8厘米；如果改做成一个长10厘米，宽9厘米的长方体框架模型，求高.9、把110厘米长的铁丝焊成一个长方体框架,长是宽的2倍，宽是高的1.5倍，求长方体的长、宽、高。

最新苏教版小学六年级数学上册第一章《长方体和正方体》测试卷及答案班级：_______姓名：_________等级：__________一．选择题1．一个长方体的油桶，底面积是215dm，高是40cm．如果每升油重0.8千克，这个油桶可装油()千克．A．480 B．4.8 C．4800 D．48【解答】解：40厘米4=分米⨯=（立方分米）1546060立方分米60=升⨯=（千克）0.86048答：这个油桶可装油48千克．故选：D．2．折叠后，()图形能围成如图的正方体．A．B．C．D．【解答】解：折叠后，图形能围成正方体．故选：A．3．小刚要做一个无盖的玻璃鱼缸，已经准备了2块长方形玻璃，其中1块长5dm、宽3dm，1块长4dm、宽3dm，还需再配3块玻璃．下列合适的是()A．2块长5dm、宽4dm，一块长4dm、宽3dmB．2块长5dm、宽4dm，一块长5dm、宽3dmC．1块长4dm、宽3dm，1块长5dm、宽4dm，1块长5dm、宽3dmD．1块长5dm、宽4dm，2块长5dm、宽3dm【解答】解：2块长5分米，宽3分米做鱼缸的前后面，2块长4分米，宽3分米做鱼缸的左右面，因此还需要配一块做鱼缸的底面，即底面的长是5分米，宽是4分米；所以还需配1块长4dm、宽3dm，1块长5dm、宽4dm，1块长5dm、宽3dm的长方形玻璃才刚合适．故选：C．4．下面的说法，正确的是()A．盛了沙子的沙坑，沙子的体积就是沙坑的容积B．甲数比乙数多14，乙数就比甲数少14C．假分数的倒数小于或等于它本身D．把一根绳子分成两段，第一段占全长的37，第二段长27米，若比较这两段绳子的长度，则第一段绳子比第二段长【解答】解：A．应该是盛满沙子的沙坑，沙子的体积才是沙坑的容积，因此，盛了沙子的沙坑，沙子的体积就是沙坑的容积．此说法错误．B．甲数比乙数多14，是把乙数看作“1”，甲相对于乙数的54；求乙数就比甲数少几分之几，是把甲数看作单位“1”，乙数比甲数少15．因此，甲数比乙数多14，乙数就比甲数少14．此说法错误．C．因为假分数等于或大于1，所以假分数的倒数等于或小于1．因此，假分数的倒数小于或等于它本身．此说法正确．D．把这根绳子的长度看作单位“1”，分成两段，第一段占全长的37，那么第二段占全长的47，第二段长2米，若比较这两段绳子的长度，则第一段绳子比第二段短．因此，若比较这两段绳7子的长度，则第一段绳子比第二段长．此说法错误．故选：C．5．一个长方体纸箱长8分米，宽5分米，高4分米，最多能装下()个棱长2分米的正方体．A．15 B．16 C．20【解答】解：长：824÷=（个），宽：522÷=（个）…1分米，高：422÷=（个），⨯⨯=（个）；42216答：最多能放16个．故选：B．6．如图所示的立方体，如果把它展开，可以是下列图形中的()A．B．C．D．【解答】解：由分析可知，如图所示的立方体，如果把它展开，是D；故选：D．二．填空题7．将一个长是4厘米、宽是3厘米、高是2厘米的铁块，放入到一个装满水的圆柱型的量杯中，溢出的水有毫升．⨯⨯=（立方厘米）【解答】解：43224=毫升24立方厘米24答：溢出的水有24毫升．故答案为：24．8．把一根长3m的长方体木料锯成四段，表面积增加2dm．96dm，这根木料原来的体积是480 3【解答】解：3米30=分米÷⨯96630=⨯1630=（立方分米）480答：这根木料原来的体积是480立方分米．故答案为：480．9．将一个大正方体切成大小相同的8个小正方体（如图），每个小正方体的表面积是18平方厘米，原正方体的表面积是平方厘米．【解答】解：小正方体每个面的面积是：1863÷=（平方厘米）大正方体每个面的面积是：3412⨯=（平方厘米）大正方体的表面积是：12672⨯=（平方厘米）答：原来正方体的表面积是72平方厘米．故答案为：72．10．用一根28分米长的铁丝做一个长方体的灯笼框架（取整分米数）．用这个框架做出的灯笼体积最大是立方分米．【解答】解：2847÷=（分米），所以长是3分米、宽和高多少2分米时体积最大，⨯⨯=（立方分米），32212答：用这个框架做出的灯笼体积最大是12立方分米．故答案为：12．11．工人师傅要把170L的油装进一些长2dm，宽1dm，高2dm的长方体小油桶里，至少需要个这样的小油桶．【解答】解：170升170=立方分米÷⨯⨯170(212)=÷1704=42.5≈（个）43答：至少需要43个这样的小油桶．故答案为：43．三．判断题12．一个无盖的长方体玻璃鱼缸，长50厘米，宽40厘米，高30厘米．做这个鱼缸至少需要玻璃74平方分米．√（判断对错）【解答】解：5040(50304030)2⨯+⨯+⨯⨯=+20005400=（平方厘米）74007400平方厘米74=平方分米答：做这个鱼缸至少需要玻璃74平方分米．题干的说法是正确的．故答案为：√．13．一根方木的体积是60立方分米，长20分米，这根方木的横截面积是3分米．⨯（判断对错）【解答】解：60203÷=（平方分米）答：这根方木的横截面积是3平方分米．故题干的说法是错误的．故答案为：⨯．14．当正方体的棱长是6厘米时，它的表面积和体积就相同．⨯．（判断对错）【解答】解：由分析得：因为体积和表面积不是同类量，所以无法进行比较，因此，当正方体的棱长是6厘米时，它的表面积和体积就相同．这种说法是错误的．故答案为：⨯．15．（2019春•长春月考）正方体的棱长是1厘米，它的表面积就是6厘米．⨯．（判断对错）【解答】解：1166⨯⨯=（平方厘米），所以正方体的棱长是1厘米，它的表面积就是6平方厘米．所以“表面积是6厘米”弄错了面积单位，这个说法是错误的．故答案为：⨯．16．如果长方体的长、宽、高都扩大3倍，则它的体积扩大3倍．⨯（判断对错）【解答】解：长方体的体积=长⨯宽⨯高，长、宽、高都扩大3倍，它的体积就扩大：33327⨯⨯=倍；所以“如果长方体的长、宽、高都扩大3倍，则它的体积扩大3倍”的说法是错误的．故答案为：⨯．17．正方体的棱长扩大3倍，它的表面积就扩大6倍，体积就扩大9倍．错误．（判断对错）【解答】解：设原来的正方体的棱长为a，则后来的正方体的棱长为3a，表面积扩大：2⨯⨯÷⨯，a a a[(33)6](6)22a a=÷，(54)(6)=；9体积扩大：33÷，[(3)]()a a33=÷，a a[27]()=；27故答案为：错误．四．应用题18．依依所在的城市将一批口罩捐赠给意大利，这是口罩包装箱的展开图，为了消毒卫生，国际快递公司要求将纸盒的每一条棱都用胶带密封，请你算一算至少需要多长的胶带？【解答】解：(12127)4++⨯314=⨯=（分米）124答：至少需要124分米长的胶带．19．吉祥食杂店要做一个长2.1m，宽40cm，高80cm的玻璃柜台，现要在柜台边都安上角铁，这个柜台需要多少米角铁？【解答】解：(2.10.40.8)4++⨯=⨯3.34=（米）13.2答：这个柜台需要13.2米角铁．20．在一个长方体上截去一个高为3厘米的长方体，表面积减少了48平方厘米，剩下一个正方体，求这个长方体的体积是多少？【解答】解：原来长方体的长和宽都是：÷÷4843123=÷=（厘米）4原来长方体的高是：+=（厘米）437原来长方体的体积是：⨯⨯=（立方厘米）447112答：这个长方体的体积是112立方厘米．21．一个长方体形状的玻璃鱼缸（无盖），量得它的长8分米，宽5分米，高6分米，水深5.4分米．（玻璃厚度忽略不计）．（1）做这个长方体玻璃鱼缸至少需要玻璃多少平方分米？（2）如果在这个鱼缸里投入一个棱长是3分米的正方体铁块．缸里的水会不会溢出？请你通过计算说明．（3）如果溢出，鱼缸里溢出多少升？如果不溢出，现在水深多少分米？【解答】解：（1）85862562⨯+⨯⨯+⨯⨯=++409660=（平方分米）196答：做这个长方体玻璃鱼缸至少需要玻璃196平方分米．（2）333(85)⨯⨯÷⨯=÷27400.675=（分米）-=（分米）6 5.40.60.675分米0.6>分米答：缸里的水会溢出．（3）33385(6 5.4)⨯⨯-⨯⨯-=-⨯27400.6=-2724=（立方分米）33立方分米3=升答：水会溢出，溢出3升．22．用一张长90cm、宽80cm的长方形铁皮，在它的四个角各剪去一个边长10cm的小正方形（如图），焊接成一个无盖的铁皮箱，这个铁皮箱的表面积是多少平方厘米？它的容积是多少升？如果每升装机油0.8千克，可以装机油多少千克？【解答】解：908010104⨯-⨯⨯=-7200400=（平方厘米）；6800-⨯--⨯⨯(90102)(80102)10=⨯⨯706010=（立方厘米）；4200042000立方厘米42=升，⨯=（千克）；420.833.6答：这个铁皮箱的表面积是6800平方厘米，它的容积是42升，可以装机油33.6千克．五．解答题23．把长24厘米、宽16厘米的长方形纸，从四个角各剪去一个边长3厘米的正方形，再折成一个无盖的长方体纸盒．求这个纸盒的容积．【解答】解：(2432)(1632)3-⨯⨯-⨯⨯=⨯⨯18103=⨯1803=（立方厘米）540答：这个纸盒的容积是540立方厘米．24．有一个完全封闭的容器，从里面量长20厘米，宽15厘米，高10厘米．平放时里面装了6厘米深的水．如果把这个容器竖起来放（如图），水的高度是多少厘米？【解答】解：201561800⨯⨯=（立方厘米），÷⨯1800(2010)1800200=÷=（厘米），9答：水的高度是9厘米．25．为迎接“五一”国际劳动节，工人叔叔要在工人俱乐部的四周装上彩灯（地面的四边不装）．已知工人俱乐部长90cm，宽55cm，高22cm，工人叔叔至少需要多长的彩灯线？【解答】解：(9055)2224+⨯+⨯=⨯+145288=+29088=378()cm答：工人叔叔至少需要378厘米的彩灯线．26．一个正方体的水箱，从里面量长是40厘米，宽是35厘米，水箱中浸没一个钢球，水深是15厘米，当取出钢球后，水深是12厘米．请问钢球的体积是多少立方厘米？【解答】解：4035(1512)⨯⨯-14003=⨯=（立方厘米），4200答：钢球的体积是4200立方厘米．27．如图，有一个长6分米、宽4分米、高2分米的长方体硬纸箱，用绳子将箱子捆扎起来，打结处共用2分米．一共要用绳子多少分米？【解答】解：6244262⨯+⨯+⨯+=+++121612242=（分米），答：一共用绳子42分米．28．将如图所示展开图形围成正方体后，哪两个面分别相对？对对对．【解答】解：如图，根据正方体展开图的特征，围成正方体后祖对旺国对达兴对发．故答案为：祖，旺，国，达，兴，发．。

六上《长方体和正方体》考点练习姓名成绩一、填空1.把一块棱长是0.6米的正方体钢坯锻造成横截面是0.09平方米的长方体钢坯，锻造成的钢坯长（）分米。

2.正方体的棱长扩大3倍，它的表面积扩大（）倍，体积扩大（）倍。

3.用3个棱长是2分米的正方体粘合成一个长方体，长方体比3个正方体少（）个面，表面积减少（）平方分米。

4、人民剧场大门前有10级台阶，每级台阶长5米，宽0.4米，高0.2米，这10级台阶一共占地( )平方米，如果用地砖铺这10级台阶，至少需要( )平方米的地砖。

5、一根长0.5米的长方体木料横截面是正方形，把它平均锯成两段，表面积比原来增加了30平方厘米。

原来这根长方体木料的体积是( )立方厘米。

6、右图是用棱长1厘米的小正方体拼成的，右图中物体表面积是( )平方厘米，体积是( )立方厘米。

7. 5平方米=（）平方分米 360立方厘米=（）立方分米=（）毫升2060立方分米=（）立方米 0.298平方分米＝（）平方厘米5升80毫升＝（）立方分米（）立方厘米＝（）立方分米8. 在下面的括号里填上适当的单位名称。

一本书的封面大小为2.8（），一瓶墨水的容积大约是60（）；一台电脑的体积是42（），一个冰箱的体积是0.3（）。

9.把一根长6分米的铁丝，做成一个长6厘米，宽5厘米，高2厘米的长方体后，还剩（）厘米。

10. 小明用一张长方形纸正好可以画上一个棱长为1（）平方厘米。

11.用6个棱长为2分米的正方体粘合成一个长方体，表面积最多减少（）平方分米。

12. 商店营业员用一根塑料带为顾客捆扎两个食品盒，每个食品盒的长、宽、高分别是17厘米、11厘米、4厘米，如右图那样捆扎一道并留下18厘米长为手提环，这样一共需要（）厘米长的塑料带。

13.用3个完全一样的小正方体拼成一个长方体，表面积减少36平方厘米，拼成的表面积是（）平方厘米。

14.将一个表面涂有红色的长方体分割成若干个体积为1立方厘米的小正方体，其中一点红色都没有的小正方体只有3块，原来长方体的体积是（）立方厘米。

苏教版数学六年级上册《长方体与正方体》）练习题（1）（长方体和正方体的认识）一、填空：1、长方体和正方体都有( ) 个面，( ) 条棱，( ) 个顶点。

2、长方体的每个面都是( )形或有一组对面是( )。

它有( )条棱，平行的( )条棱都相等。

3、相交于长方体一个顶点的三条棱的长度分别叫做它的（）、（）和（）。

4、长方体有（）个面，从不同的角度观察一个长方体，最多能看到（）个面。

5、一个长方体的长是5分米，宽是4分米，高是3分米，6个面中最小的一个面的面积是（），最大的一个面的面积是（）。

6、一个长方体，长4米，宽3米，高2米，它的占地面积最大是（）平方米。

7，长方体的右侧面面积是12平方厘米，前面面积是8平方厘米，上面面积是6平方厘米，这个长方体的长、宽、高分别是（）、（）、（）。

二、选择：1、一个长方体水池，长20米，宽10米，深2米，这个水池占地（）平方米。

A、200B、400C、5202、下面的图形中，能按虚线折成正方体的是（）。

3、从一个体积是30立方厘米的长方体木块中，挖掉一小块后(如下图) ，它的表面积( ) 。

A．和原来同样大 B．比原来小 C．比原来大 D．无法判断4、用一根52厘米长的铅丝，正好可以焊成长6厘米，宽4厘米，高（）厘米的长方体教具。

A、2B、3C、4D、5三、计算下面每个图形的棱长和。

1、一个长方体，长5分米，宽3分米，高4分米，求它的所有棱长的和。

2、用钢筋做一个长和宽都是3.5分米，高是10厘米的长方体，需多少分米的钢筋？3、棱长是4分米的正方体，棱长和是多少分米？4、一个长方体的棱长和是36厘米，从一个顶点出发的三条棱的和是多少厘米？5、同一根长96厘米的铁丝折成一个最大的正方体框架，求正方体框架的棱长。

6、一个长方体的长是15厘米，宽是12厘米，棱长总和是148厘米，求它的高。

7、两根同样长的铁丝焊一个长方体和正方体，长方体长7厘米，宽5厘米，高3厘米，求正方体的棱长。