当前位置：文档之家 › 第六章 结构振动特征值问题的矩阵摄动法

第六章 结构振动特征值问题的矩阵摄动法

  • 格式：doc
  • 大小：297.00 KB
  • 文档页数：8

下载文档原格式

  / 8

合集下载

结构动力学中的特征值反问题

结构动力学中的特征值反问题

南京航空航天大学博士学位论文结构动力学中的特征值反问题姓名：***申请学位级别：博士专业：一般力学与力学基础指导教师：***20060601南京航空航天大学博士学位论文摘要本文研究了结构动力学中的特征值反问题，包括弹簧-质点系统振动反问题、离散梁振动反问题、阻尼振动系统的振动反问题以及振动杆结构探伤问题。

全文主要包括以下内容：首先，研究了弹簧-质点系统的振动反问题。

对二自由度简单连接度弹簧-质点系统分别通过加刚性约束、弹性约束和质量摄动得到修改系统，研究了利用原系统和修改系统的两组特征值（频率）和修改量识别系统的物理参数问题，给出了解的表达式。

对于多自由度简单连接度弹簧-质点系统，研究了增容修改系统的频率反问题。

提出了由多自由度简单连接弹簧-质点系统的四个和五个特征对（频率和模态）识别系统物理参数的振动反问题，分别研究了解的存在性，给出了解的表达式、相应算法和算例。

提出并研究了一类混合连接弹簧-质点系统的振动反问题，提出了利用三个特征对（频率和模态）以及部分系统物理参数识别系统其它物理参数的振动反问题，研究了解的存在性，给出了解的表达式、相应算法和模型算例。

其次，研究了有限差分离散梁振动反问题，利用有限差分法得到振动梁的弹簧-质点-刚杆模型，质量矩阵为对角矩阵而刚度矩阵为对称五对角矩阵。

提出了基于三个特征对的频率模态反问题，研究了解的存在性，给出了解存在惟一的充要条件和解的表达式、数值算法和算例。

再次，研究了阻尼振动系统中的二次特征值反问题。

研究了阻尼弹簧-质点系统的物理参数识别，包括：由全部频率信息模态识别阻尼振动系统的结构物理参数；由部分频率模态信息识别比例阻尼振动系统的结构物理参数；由两对频率模态信息识别比例阻尼振动系统的结构物理参数；由频率模态信息识别非比例阻尼振动系统的结构物理参数。

对每种提法分别研究了问题解的存在性，给出了数值算法，并对每种问题给出了阻尼振动模型算例。

最后，研究了振动杆结构探伤的特征值反问题。

《结构力学课件》矩 阵 位 移 法

《结构力学课件》矩 阵 位 移 法

将（17—21）及（17—25） T F 式代入上式得： e
K
T
e
T e
e
F
T
K
T e
e 另 [T]T[ K ] [I]=[K]e 则 用结分点块式表示为：
{F}e=[K]e{}e
e Fi e F j e Kii e K ji e e Kij i e Ke jj j
• 注：1） F , 为结构坐标的杆端力和杆端位移。 • 2） Kij e 表示单元e 的j端三个位移分别产生单位位移时在i 端各力 • 分量分别产生的力。 • 3） Kii , Kij , K ji , K jj 分别为单元在结构整体坐标中刚度。
e e

返回 下一张 上一张 小结图17-4来自返回 下一张 上一张 小结
• 17.1.6 引入支承条件，求结点位移
• 已知上例支承条件 1 =0，连同已获得的[K]，以及各结点 荷载值（M1、M2、及M3=0）一起代入基本方程（7—6）式中，得：
4i1 2i 1 0 2i1 4i1 4i 2 2i 2 0 0 2i 2 2 4i 2 3 M1 M 2 0
｛
矩阵位移法是以位移法为力学原理，应用矩阵理论，以电子 计算机为工具的结构分析方法。 有限单元法包含两个基本环节：一是单元分析；一是整体分析。
在矩阵位移法中：单元分析的任务是建立单元刚度方程，形 成单元刚度矩阵——讨论任意坐标系中单元刚度方程的通用形式； 整体分析的任务是将单元及合成整体，由单元刚度矩阵按照 刚度集成规则形成整体刚度矩阵，建立整体结构的位移法基本方 程，从而求解。 直接由单元刚度矩阵导出整体刚度矩阵的集成规则，是矩阵 位移法的核心内容。

高等结构振动学-第6章-结构振动特征值问题的矩阵摄动法

高等结构振动学-第6章-结构振动特征值问题的矩阵摄动法

)
({u0(s)}T [K1]{u1(i)} (0i){u0(s)}T [M1]{u1(i)}
1(i){u0(s)}T [M 0 ]{u1(i)} 1(i){u0(s)}T [M1]{u0(i)})
（6－29）
当 i s 时， ci(2) 的确定如下：
n
以
{u
(i 0
)
}T
)}
所以，代入（6－8）式得：
{u1(i)}
n s 1
(i ) 0
1

( s ) 0
({u0(s)}T [K1]{u0(i)} (0i){u0(s)}T [M1]{u0(i)}){u0(s)}
si

1 2
({u0(i)}T
[M1]{u0(i)}){u0(i)}
故一阶摄动解为：
（6－22） （6－23）
)}

{u0(i
)
}T
[M1
]{u1(i)
}

{u1(i
)}T
[
M
1
]{u0(i
)})
（6－32）
故特征向量的二阶摄动解为：
{u2(i)}
n s 1
(i) 0
1

( s ) 0
({u0(s)}T [K1]{u1(i)}
si

(i 0
){u0( s
)}T
[
M
1]{u1(i
)}

{u (i) (s) 10
n

(i 0
)
[
M
0
]
c (1) s
{u 0( s
)
}

(i) 0

结构动态设计的矩阵摄动理论(陈塑寰著)PPT模板

结构动态设计的矩阵摄动理论(陈塑寰著)PPT模板

05 第3章 重频结构振动分析 的矩阵摄动理论
第3章 重频结构振动分析的矩阵摄动理论
3.1 引言
1
3.2 重频模态的摄动理
论
2
3.3 重频模态一阶摄动
3
的近似模态展开法
3.4 重频模态一阶摄动
计算的高精度模态展开法
4
3.5 利用重频模态计算
5
重频模态导数的精确方法
3.6 计算模态向量一阶
摄动的胡海昌方法
结构动态设计的矩阵摄动理论(陈 塑寰著)
演讲人
2 0 2 x - 11 - 11
01 序
序
02 前言
前言
03 第1章 结构振动分析的有 限元方法
第1章 结 构振动分析 的有限元方 法
01 1 .1 引言
02 1 .2 离 散 系 统 的
hamilton变分原理
03 1 .3 建 立 结 构 振动 04 1 .4 单 元 力 学 特性
法
2.3.2 和 rayleigh商相 结合的摄动法
2.3.3 数值 例子
第2章 孤立特征值的矩阵摄动理论
2.4 振型一阶导数的高精度截尾模态展开法
01
2.4.1 计算振 型一阶导数的 wangb.p.方法
02
03
2.4.2 计算振 型一阶导数的高 精度截尾模态展 开法
2.4.3 数值例 子
第2章 孤立特征 值的矩阵摄动理论
1.11.1 中心差分
法
1.11.2 wilson-
θ方法
1.11.3 newmar
k方法
04 第2章 孤立特征值的矩阵 摄动理论
第2章 孤立特征值的矩阵摄动理论
2.1 引言
2.3 摄动法的改进

结构力学(I)-结构静力分析篇6 矩阵位移法解析

结构力学(I)-结构静力分析篇6 矩阵位移法解析

FP 结点
1,2,3 ----结构结点编码（总码） (1,2,3) ----结点位移编码
1 2 ----杆端结点编码（局码）
1 2 ----单元编码
1
1
3(5,6)FP
2 2
2
1
1(1,2)
2(3,4)
单元方向 1 2
11 / 105
第六章 矩阵位移法 §6-2 单元刚度方程
建立单元的结点力和结点位移之间关系的过 程称单元分析，形成的方程称单元刚度方程。
6EI l2 2 EI l
12EI l3
6EI l2 12 EI l3
6EI l2
6 EI l2 2 EI l
6EI l2 4 EI l
1 2 3 4
e
刚度方程
18 / 105
第六章 矩阵位移法
12 EI
l3 6EI
k
e
l2
12EI l3
6 EI l2
位移法 是先求结点位移，再换算成力，该法的计 算自动化和通用性强，目前广为采用。
6 / 105
第六章 矩阵位移法
二、基本假设和基本原理
线弹性、小变形。满足叠加原理、功能原理
三、结构矩阵分析的基本思路
化整为零
（单元分析）
集零为整
（结点力平衡、位移协调）
7 / 105
第六章 矩阵位移法
四、拟解决的问题
6EI l2
1
4EI l
2
6EI l2
3
2EI l
4
F3e
12EI l3
1
6EI l2
2
12EI l3
3
6EI l2
4Hale Waihona Puke F4e6EI l2

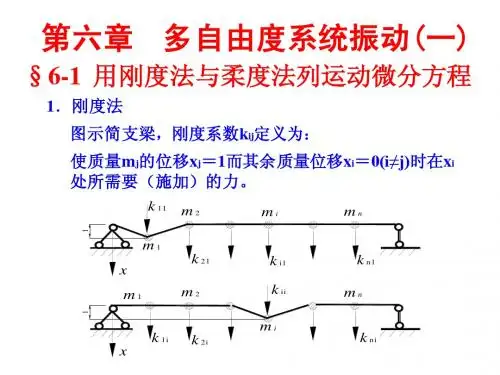
6《结构动力学》-第六章

6《结构动力学》-第六章

x2
x3
k4
x4
k5
x5
m2
k3
m3
m4
m5
解：首先用力使m1产生单位位移，并用力使其余质量不动， 首先用力使 产生单位位移，并用力使其余质量不动， 则需要给m 的力为k 的弹性力和， 则需要给 1的力为 1与k2的弹性力和，即k11＝k1+k2。此时 m2需加力为 2，沿x的负方向，即k21＝-k2，其余质量不必 需加力为k 的负方向， 的负方向 施加任何力， 施加任何力，即k31＝k41＝k51＝0。 。 用类似方法可得其余刚度系数，于是有： 用类似方法可得其余刚度系数，于是有：
m2上加单位力，各质量的位移分别为： 上加单位力，各质量的位移分别为：
a12 = 1 k1 a 22 = 1 1 + k1 k 2 a 32 = a 22 = 1 1 + k1 k 2
〈例〉求图示三自由度系统的刚度矩阵和柔度矩阵。 求图示三自由度系统的刚度矩阵和柔度矩阵。
k1
m1
x1 k2
x2
x3 m3
LL
用矩阵符号可写成： 用矩阵符号可写成：
LL
mn &&n = −k n1 x1 − k n 2 x2 − LL − k nn xn + Fn (t ) x
& [M ]{X& }+ [K ]{X } = {F (t )}
〈例〉求图示五自由度系统的刚度矩阵。 求图示五自由度系统的刚度矩阵。
k1
m1
x1 k2
或写成： 或写成：
& {X } + [A][M ]{X& } = {0}
在刚度矩阵[K]非奇异条件下，柔度矩阵 与刚度矩 在刚度矩阵 非奇异条件下，柔度矩阵[A]与刚度矩 非奇异条件下 存在如下的互逆关系： 阵[K]存在如下的互逆关系： 存在如下的互逆关系

振动分析矩阵迭代法

振动分析矩阵迭代法

1 2
2


333Y3(0)

1 3
2

...

这些惯性力产生的挠度是
v (1) 1

~ff
( I
0)

~f
*
m

112Y1(
0)


223Y2(
0)

1 2
2

2

333Y3(0)

1 3

...
(4) 1
1.000 17.121
0.320 5.287
v v (4)
(5)
1
1
1.000 17.082
0.653 11.121 0.650 11.082
0.306 5.182 0.303 5.159
12

max(v1(s1) )
(s)
max(v1 )

v(4) 11
v(5) 11
210.77
缺点：柔度矩阵是满阵，与窄带刚度矩阵相 比的运算相比会使计算效率降低。
补充：基于刚度矩阵的动力矩阵： E m1K 由于收敛于最高阶阵型，所以实际应用不大。
逆迭代法
基本思路:逆迭代法是利用是利用刚度矩阵窄 带性质的首选方法，因为其是使用刚度矩 阵的逆矩阵，所以此法向最低阵型收敛。 为保证刚度矩阵K的窄带性质，不形成动力 矩阵E，而是把假定的位移向量和质量举证 结合，然后求解基于刚度的平衡联立方程 组得到改进的位移向量，解方程组是常采 用LU分解法。
用迭代法反复进行迭代，就可以得到体系 的最低频率和相应的阵型。
迭代收敛性的证明：
Stodola法和Holzer法 Stodola法是先假定初始振型并不断迭代调整

第六章 摄动方法

第六章 摄动方法

t a, b 可以是无穷区间，或闭区间， 1 ，设 f t
为连续函数; F 对 t 连续，对其余变量在其变化范 围内解析，则该问题称为摄动问题 P ， 0 时对应的问题称为退化问题 P0 ，若 P 问题的解 u t, 当 0 时，对 t a, b 有一致渐近幂级数，即
" i i 1
(10)
第二步：将所有的项都按小参数(这里是 a )展开，使
每一项都可写成一个 a 的幂级数。利用 sin x 的展开
式，上式中的第二项为：
a sin ai ai i 0
1
a i i a a i a a a … i i 0 3! i 0
1 1 1 cos t cos3t t sin t 192 16 192
注意到，上面的求解都是形式上的。设
t , i t i
i 0
(12)
由此可得一阶近似：
t, 0 t 1 t
0
第六章 摄动方法
摄动方法是一种重要的应用数学方法，它在力学，物 理和众多的工程学科中有着广泛的应用。 工程技术中归纳出来的数学模型，其中不少是含有小 参数的，且方程的准确解难以获得。
利用计算机进行数值积分，虽然可以给
出定解问题的数值解，但很难给出物理现象的 全貌和一般规律，利用摄动法可以求得解析形 式的近似解，对物理系统进行相当精确的定量 和定性讨论。这里，主要讨论正则摄动方法 和奇异摄动方法。
§1 正则摄动方法
例1：已知初值问题
dy 2 1 y dx y 0 0
（1）
的解
yy
0

刚架结构振动特性分析的精细传递矩阵法

刚架结构振动特性分析的精细传递矩阵法
ｒ ，、
（） ８
（） ９
舞＝ 训
（） ３
如全 梁划分成 段 ， 则有 ：
Ｓ ＝ １ Ｔ Ｌ Ｓ ＝Ｔ ０ Ｌ Ｔ１ ｏ Ｓ
将式 （） ２ 写成 矩 阵 的 形 式 为 ：
：
其中， Ｔ为梁 的总体传递 矩阵。
将结 构 的 两 端 边 界 条 件 引入 式 （ ） 到 频 率 方 程 ： （ ） ， ９得 ｆ ＝０
３ 自振频 率 的求解
图 １ 直 梁 横 向 自 由振 动 图
各段梁的传 递矩 阵确定之后 ， 任一段 的状态 向量可 由式 （ ） ８ 求
得：
由 结 构 的 几 何 、 理条 件 ｌ 得 ： 物 ４ ｊ
ｄｕ ｄ ｘ ｄ Ｍ ｄ Ｅ１ ｘ
＝ Ｅ１
Ｓ ＝ ＴＴｉ１ ＴＬ Ｓ ｉ 一 Ｌ Ｔ１ ０
第 ３ ６卷 第 １ ２期 ２０ １ ０ 年 ４ 月
山 西 建 筑
Ｓ ＨＡＮＸＩ ＡＲＣＨＩ ＴＥＣＴＵＲＥ
Ｖ０ ３ Ｎｏ １ １ ６ ．２
Ａｐ． ２ １ ｒ ００
・６ ・ １
文 章 编 号 ：０ ９６ ２ （０ ０ １ —０ １０ １ ０ —８５ ２ １ ）２０ ６ —２
山 西 建 筑
Ｓ ＨＡＮＸＩ ＡＲＣＨＩ ＴＥＣｒＵＲＩ
Ｖｌ． ０ ３６Ｎｏ １ 】 ．２
Ａｐ ． ２ ０ ｒ ０１
Ａ Ｓ
运用 频率搜索法 即可求 出各 阶振 动频 率 ，Ｊ ： 。 （ ＝ｌ ｎ）
Ｆ＇ ， Ｅ， ， Ａ ，
ｌ ７ ｒ ０ １ ０ ｏ Ｊ
０ Ａ ０
ｒ ｌｕ
１ ０
０ 。 ０ １ｌ
ｌ ０ ２ ０
＿ Ｑ
（） ４

机械振动中的特征值问题

机械振动中的特征值问题

机械振动中的特征值问题机械振动是指系统在某一位置（通常是静平衡位置，简称平衡位置）附近所作的往复运动。

显然这是一种特殊形式的机械运动。

人类的大多数活动都包括这样或那样的机械振动。

例如，我们能听见周围的声音是由于鼓膜的振动；我们能看见周围的物体是由于光波振动的结果；人的呼吸与肺的振动紧密相关；行走时人的腿和手臂也都在作机械振动；我们能讲话正是喉咙（和舌头）作机械振动的结果。

早期机械振动研究起源于摆钟与音乐。

至20世纪上半叶，线性振动理论基本建立起来。

欧拉（Euler）于1728年建立并求解了单摆在阻尼介质中运动的微分方程。

1739年他研究了无阻尼简谐强迫振动，从理论上解释共振现象。

1747年他对n个等质量质点由等刚度弹簧连接的系统列出了微分方程组并求出精确解，从而发现系统的振动是各阶简谐振动的叠加。

1760年拉格朗日（Lagrange）建立了离散系统振动的一般理论。

最早研究的连续系统是弦线。

1746年达朗伯（d’Alembert）用片微分方程描述弦线振动而得到波动方程并求出行波解。

1753年伯努利（Bernoulli）用无穷多个模态叠加的方法得到弦线振动的驻波解。

1759年拉格朗日从驻波解推得性波解，但严格的数学证明直到1811年傅里叶（Fourier）提出函数的级数展开理论才完成。

一个振动系统本质上是一个动力系统，这是由于其变量如所受到的激励（输入）和相应（输出）都是随时间变化的。

一个振动系统的响应一般来说是依赖于初始条件和外部激励的。

大多数实际振动系统都十分复杂，因而在进行数学分析时把所有的细节都考虑进来是不可能的。

为了预测在指定输入下振动系统的行为，通常只是考虑那些最重要的特性。

也会经常遇到这样的情况，即对一个复杂的物理系统，即使采用一个比较简单的模型也能够大体了解其行为。

对一个振动系统进行分析通常包括以下步骤。

步骤1，建立数学模型。

建立数学模型的目的是揭示系统的全部重要特性，从而得到描述系统动力学行为的控制方程。

机械振动中的特征值问题

机械振动中的特征值问题

机械振动中的特征值问题机械振动是指系统在某一位置（通常是静平衡位置，简称平衡位置）附近所作的往复运动。

显然这是一种特殊形式的机械运动。

人类的大多数活动都包括这样或那样的机械振动。

例如，我们能听见周围的声音是由于鼓膜的振动；我们能看见周围的物体是由于光波振动的结果；人的呼吸与肺的振动紧密相关；行走时人的腿和手臂也都在作机械振动；我们能讲话正是喉咙（和舌头）作机械振动的结果。

早期机械振动研究起源于摆钟与音乐。

至20世纪上半叶，线性振动理论基本建立起来。

欧拉（Euler）于1728年建立并求解了单摆在阻尼介质中运动的微分方程。

1739年他研究了无阻尼简谐强迫振动，从理论上解释共振现象。

1747年他对n个等质量质点由等刚度弹簧连接的系统列出了微分方程组并求出精确解，从而发现系统的振动是各阶简谐振动的叠加。

1760年拉格朗日（Lagrange）建立了离散系统振动的一般理论。

最早研究的连续系统是弦线。

1746年达朗伯（d’Alembert）用片微分方程描述弦线振动而得到波动方程并求出行波解。

1753年伯努利（Bernoulli）用无穷多个模态叠加的方法得到弦线振动的驻波解。

1759年拉格朗日从驻波解推得性波解，但严格的数学证明直到1811年傅里叶（Fourier）提出函数的级数展开理论才完成。

一个振动系统本质上是一个动力系统，这是由于其变量如所受到的激励（输入）和相应（输出）都是随时间变化的。

一个振动系统的响应一般来说是依赖于初始条件和外部激励的。

大多数实际振动系统都十分复杂，因而在进行数学分析时把所有的细节都考虑进来是不可能的。

为了预测在指定输入下振动系统的行为，通常只是考虑那些最重要的特性。

也会经常遇到这样的情况，即对一个复杂的物理系统，即使采用一个比较简单的模型也能够大体了解其行为。

对一个振动系统进行分析通常包括以下步骤。

步骤1，建立数学模型。

建立数学模型的目的是揭示系统的全部重要特性，从而得到描述系统动力学行为的控制方程。

特征值组的摄动法

特征值组的摄动法

特征值组的摄动法摄动法是一种研究复杂系统时常用的数值积分方法。

它将一个复杂的时间曲线上的某种状态，划分为若干个离散时间步，每一步分别用固定的起始条件和特征值组的摄动法来计算时间步的终止条件，从而求得被研究的状态。

在本文中，我们将研究特征值组的摄动法，并详细分析其原理及特点。

特征值组的摄动法基于以下这一基本思想：在一个时间步中，具有相同特征值的系统只会有一个状态。

即，如果两个系统具有相同的特征值，那么它们在任何时刻上它们所处的状态也是一样的。

这里特征值指的是某个系统的某些性质，如物理量，动能，势能等等。

因此，一个系统的某种状态可以通过它的特征值来描述。

基于这一思想，我们可以定义一组特征值组，它们在同一个时间步中代表着某一个特定的状态。

在每一个时间步，系统的特征值会发生变化，但是一组特征值组始终保持不变，因此，它们可以用来描述系统在某一个特定时刻的状态。

摄动法就是根据这一思想，划分一个复杂时间曲线上的某种状态，并用下一个特征值组的摄动法，来求得它的未来状态。

具体来说，特征值组的摄动法可以描述为：在每个时间步，我们以一组初始特征值组S0作为输入，根据它们求得下一步的特征值组S1，然后以S1作为输入，求得更后一步的特征值组S2，以此类推，直至找到最终的特征值组Sf，它代表着某个特定时刻的系统状态。

一般而言，特征值组的摄动法比一般时间步积分方法更加精确和可靠，它有两个主要优点：首先，特征值组的摄动法可以在每个时间步较准确地把系统的状态描述出来，这使得它在研究超过一定复杂度的系统时可以比较精确地模拟出来。

其次，特征值组的摄动法可以有效地刻画出系统的变化特性，无论是系统是稳定还是混沌，它都能很好地描述出来。

因此，特征值组的摄动法是一种非常有用的积分方法，它可以有效地模拟复杂系统的状态，而且因为其精确性和可靠性，特征值组的摄动法已经被用于研究复杂系统中的各种相关问题。

本文介绍了特征值组的摄动法的原理及特点，它是一种有效的积分方法，可以非常准确和可靠地模拟出复杂系统的状态，在许多系统研究领域得到广泛应用。

第六章 结构振动特征值问题的矩阵摄动法

第六章 结构振动特征值问题的矩阵摄动法

第六章 结构振动特征值问题的矩阵摄动法§6.1 概述工程振动问题中经常遇到结构有小改动的情形，例如结构的制造误差、结构的小修改设计、对结构参数改变进行灵敏度分析等。

这些情况都有一个共同的特点，就是结构的参数仅发生很小的变化。

结构参数的小变化所引起的结构振动特性变化问题，对工程结构优化设计有重要意义。

经典的方法是每修改一次方案就需要求解一次结构的固有特性，即求解广义特征值问题。

这对于大型结构的振动分析，是非常麻烦的。

我们希望能找到一种能够利用修改前结构的固有特性信息，且计算量小的方法，来解决上述问题。

矩阵摄动法就是这种结构特征值重分析和灵敏度快速分析的计算方法。

§6.2 孤立特征值的摄动法对离散系统特征值问题，假定已经得到了其特征对的解：（6－1）分别为参数未变化的原结构刚度矩阵和质量矩阵，第个特征值，为第阶固有频率，为第阶特征向量（固有模态）。

结构参数的变化或修改设计一般通过刚度矩阵和质量矩阵的改变反映出来。

即（6－2）（6－3）称为小参数。

先看是单根的情形。

上标代表第个根，下标代表参数未变化的原结构。

从物理意义上知道，绝大多数情况下，质量阵和刚度阵只有小变化时，特征值和特征向量也只有小量变化，根据摄动理论，特征值和特征向量按小参数展开为：（6－4）代入方程（6－1），略去以上的项，比较同次幂的系数，得到： }]{[}]{[)(00)(0)(00i i i u M u K λ=][],[00M K i 2)(0)(0)(i i ωλ=)(0i ωi }{)(0i u i ][][][10M M M ε+=][][][10K K K ε+=ε）（i 0λ)(i i 0)(ε+++=+++=)(22)(1)(0)()(22)(1)(0)(}{}{}{}{i i i i i i i i u u u u λεελλλεε)(2εO ε（6－5）（6－6）（6－7）、、、分别是特征值与特征向量的第一阶摄动和第二阶摄动。

结构动力学振动分析的矩阵迭代法

结构动力学振动分析的矩阵迭代法

（13-28）
在试探向量中消除第一振型分量的方便方法是应用滤型 矩阵 S1
~
其中
（0） 2

（0） 2
1 T (0 ) (0 ) - φ1 φ 1 m 2 S1 2 M1
（13-29）
1 T S1 Ι - φ 1φ 1 m M1
（13-30）
在这种情况下，式（13-5）可以写成
1 （1） （0） D ~ ~2 2 2 2
克拉夫书P205 例题E13-1 通过计算图E11-1的三层建筑框架的第一振型和频率来说 明矩阵迭代法。虽然用例题E11-1中导得的刚度矩阵求逆可以很容易 求得该结构的柔度矩阵，但是为了说明柔度矩阵的求法，这里对每 一个自由度相继施加单位荷载进行推导。根据定义，由这些单位荷 载所产生的位移表示柔度影响系数。

（0） 1

(0 )
φY
（0） 1 1
φ Y
（0） 2 2
φ Y
（0） 3 3
（13-14）
第一振动频率的振动形状所对应的惯性力为
(0 ) 2 f(0) 12m1 1 m(0)
2 2 2 ( / ) 记 1 ，展开得 n 1 n
（13-15）

（ 1） 1
D
（0） 1
（13-7）
（ 1） 来进行规格 1
该向量除以向量中最大的元素max（ 化，得到改进的迭代向量：
）

（1） 1


max （ ）ຫໍສະໝຸດ （1） 1 （1） 1（13-8）
设 k 为向量中任一自由度，频率近似值为：

2 1
(1)
(0 ) k1 (1) k1

(同济大学)结构动力学教程 第六章 结构动力学中常用的数值方法

(同济大学)结构动力学教程 第六章 结构动力学中常用的数值方法

（2） 求解位移向量： [K ]{x}t+θ∆t = {R}t+∆t
{x}t+∆t = a4 ({x}t+θ∆t − {x}t ) + a5{x}t + a6{
（3） 求解加速度、速度、位移向量：{x}t+∆t = {x}t + a7 ({x}t+∆t + {x}t ) {x}t+∆t = {x}t + ∆t{x}t + a8 ({x}t+∆t + 2{x}
（{Q}t+θ∆t = {Q}t +θ ({Q}t+∆t −{Q}t )） 以位移 {x}t+θ∆t 为未知量建立求解方程，即：
[K ]{x}t+θ∆t = {R}t+θ∆t
式中，
[K ] = [K ] + 1 [M ] + 3 [C]
(θ∆t ) 2
θ∆t
{R }t +θ∆t
= {Q}t
+ θ ({Q}t+∆t
x
xt+∆
t + ∆t
用同样方法处理位移
泰勒展开：{x}t+∆t
= {x}t
+ {x}t ∆t +
1 {~x}∆t 2 2
类似地设 t → t + ∆t 时间间隔内：{x} = {x}t + 2δ ({x}t+∆t − {x}t )
(0 ≤ δ ≤ 0.5)
{x}t+∆t = {x}t + {x}t ∆t + (0.5 − δ ){x}t ∆t 2 + δ {x}t+∆t ∆t 2
与原矩阵a相关联的矩阵设矩阵a的特征值为对应的特征向量为的特征值为对应的特征向量为的特征值为对应的特征向量为的特征值为对应的特征向量仍为非奇异则的逆矩阵存在为其特征值相似即有可逆矩阵存在使的特征值也为特征向量为特征值的和与积设矩阵的特征值为则有供校核用特征向量规范化设矩阵的特征向量为的特征向量

矩阵摄动法

矩阵摄动法

孤立特征值情况的矩阵摄动法
一、基本公式：
一阶摄动公式
二阶摄动公式
二、数值例子
图1
图1表示一个质量弹簧系统，设此系统的质量阵和刚度阵为错误！未找到引用源。

错误！未找到引用源。

取错误！未找到引用源。

分别为：
错误！未找到引用源。

错误！未找到引用源。

固有频率误差计算公式为：
振型向量误差计算公式为：
三、计算结果分析
1.各频率误差对比
结构参数改变
误差
图2 第一频率
结构参数改变
误差
图3 第二频率
结构参数改变
误差
图4 第三频率
2.各振型向量误差对比
结构参数改变
误差
图5 第一振型
结构参数改变
误差
图6 第二振型
结构参数改变
误差
图7 第三振型
可以看出在结构参数改变量在15%以下时，用一阶摄动法是可行的，当然使用二阶摄动法更精确。

当结构参数改变30%时，用二阶摄动法是可行的，使用一阶摄动法误差较大，不宜采用。

当结构参数改变40%时，即使用二阶摄动法，固有频率的平均误差仍有8.7%，振型向量平均误差仍有2.8%，这个误差是比较大的。

说明这时二阶摄动法也得不到足够的精度，需要用更高阶摄动法。

四、小结
通过本例，我们得到一些结论。

无论结构参数如何改变，本例的二阶
摄动法总是比一阶摄动法有更高的计算精度。

当结构参数改变小于15%时，用一阶摄动法已足够，可以不用二阶摄动法。

但当结构参数变化为15% ~ 30%时，就必须用二阶摄动法才能得到足够的计算精度。

特征值解法——精选推荐

特征值解法——精选推荐

特征值解法《结构动⼒学》⼤作业结构⼤型特征值问题的求解0810020035 吴亮秦1振动系统的特征值问题1.1实特征值问题n ⾃由度⽆阻尼线性振动系统的运动微分⽅程可表⽰为：[]{}[]{}()M u K u F t += （1.1）其中，{}u 是位移向量，[]M 和[]K 分别是系统的质量矩阵和刚度矩阵，都是n 阶正定矩阵，()F t 是激励向量。

此系统的⾃由振动微分⽅程为[]{}[]{}0M u K u += （1.2）设其主振型为： {}{}sin()u v t ω?=+ （1.3）其中，{}v 为振幅向量，ω为圆频率，?为初相位。

将(1.3)代⼊⾃由振动微分⽅程(1.2)，得：[]{}[]{}K v M v λ= （1.4）其中2λω=，(1.4)具有⾮零解的条件是()[][]det 0M K λ-= (1.5)式(1.4)称为系统的特征⽅程，由此可以确定⽅程的n 个正实根1{}n i i λ=，称为系统的特征值，1{}n i i ω=称为系统的固有频率，{}i v （i=1,2,…..n ）为对应于特征值的特征向量或称为系统的振型或模态。

因为[]M 矩阵正定，则[]M 有Cholesky 分解：[][][]TM L L = (1.6)其中，[]L 是下三⾓矩阵。

引⼊向量{}x 满⾜：{}[]{}Tx L v =，则：1{}([]){}T v L x -= (1.7) 代⼊(1.4)，得：([][]){}0I P x λ-= (1.8)其中，()11[][][][]TP L K L --=，式(1.8)称为标准实特征值问题。

1.2复特征值问题多⾃由度阻尼⾃由振动系统的运动⽅程为如下⼆阶常系数微分⽅程组：[]{()}[]{()}[]{()}0 M x t C x t K x t ++= (1.9) 其中 []M ，[]C ，[]K 分别是n 阶的质量、阻尼和刚度矩阵，{()}q t 是n 维可微向量函数。

大型结构振动分析方法

大型结构振动分析方法

对于等截面杆均匀杆，其单元质量矩阵为：
6.1.3 坐标转换
140 0 0 70 0 0
0
156
22l
0
54
13l
Μe
ml 420
0 70
22l 0
4l 2 0 13l 0 140 0
3l 2
0
0 54 13l 0 156 22l
0
13l 3l 2
0
22l
4l 2
单元特性矩阵是在局部坐标系下建立的，但是在考虑节点力的平衡和位移连续
在动力问题中，位移是空间坐标和时间坐标的函数。一般采用在空间中 离散结构的方法。
单元与结点划分： 单元：均质等截面直杆。 结点：杆件两端、断面突变位置、集中质量位置。
基本未知量：结点的位移和转角。 由变形协调条件可知，某结点的位移也就是汇交于此结点处的各
杆的杆端位移。确定了以结点位移为参数来表达杆内任一点位移函数 后，不难进一步写出惯性力、阻尼力、弹性内力等各种量的表达式。 这样通过限单元法便将一个原无限自由度体系动力问题转变成一个以 有限个结点位移为广义坐标的多自由度体系的动力问题。
(1)外荷载作用下的杆端力列阵 FGe
单元两端位移和转角为零。单元 上作用任意分布的外载荷，计算 该外载荷引起的杆端的弯矩。
杆元作用任意载荷，图（a）给出 了杆端力的正向。 另假设一个杆元，没有外载荷作
用，仅在i端发生单位角位移。
功的互等定理：图(a)杆元载荷在图(b)杆元变形上做的功等于图(b)
x l u (l,t) u j (t)
可解出
a0 (t) ui (t)
1 a1(t) l [u j (t) ui (t)]
u
(
x,

孤立特征值情况的矩阵摄动法

孤立特征值情况的矩阵摄动法

(17)
三、二阶摄动公式
为了得到更精确的摄动解，需要用到二阶摄动。根据展开定理，将 xi 2 按 x10 , x20 ,, xn0 展开
xi 2 k 2 xk 0
k 1
n
(18)
3
将（18）式代入(8-3)，并左乘 x k 0 ，得
T T xk 0 K 0 k 2 xk 0 xk 0 K1 xi1 k 1 T T T i 0 xk 0 M 0 k 2 xk 0 xk 0 (i 0 M 1 xi1 i1 M 0 xi1 i1 M 1 xi 0 ) i 2 xk 0 M 0 xi 0 k 1 n n
后的系统或称摄动系统）的特征值问题及相应的正交规范条件是 (4) (5)
其中， i 为新系统的特征值， xi 是相应的特征向量。 如果原系统的 i 0 各不相同，且相互间距不小，此时就称 i 0 为系统（1）的孤立特征值。 在这种情况下，当 M1 、 K1 很小时，新系统的特征值 i 及相应的 xi 均只有小变化。根据 摄动理论，可将 i 、 xi 按小参数 展开成幂级数（因此，胡海昌院士称其为小参数法） ，即
i i 0 i1 2 i 2 ( 3 )
xi xi 0 xi1 2 xi 2 ( 3 )
1
(6) (7)
现在来确定 i1 ， i 2 ， xi1 ， xi 2 ，为此，将（6） 、 （7）式代入（4）式得
(K0 K1 )(xi 0 xi1 2 xi 2 ) (i 0 i1 2 i 2 )(M 0 M1 )(xi 0 xi1 2 xi 2 )
(19)
i 2 xiT0 (K1 xi1 i 0 M1 xi1 i1M 0 xi1 i1M1 xi 0 )

第6章 结构振动分析的近似方法(中英文)

第6章 结构振动分析的近似方法(中英文)
x1 , x 2 , , x j 处有集中质量
M 1 , M 2 , , M j
，即横隔梁的简化
集中质量。 如图：
Page 14
6.1 瑞利法(Rayleigh method)：——连续体系
对于无阻尼固有振动，梁的位移可表示为
y ( x, t ) ( x) sin(t )
2 n max R X
2 n R X k min max L1 0 L 0 2 Lk 1 0
(6.9)
k 2,3,, n
(6.10)
式中， ( x)为满足梁的位移边界条件的近似振型函数。
梁的动能(kinetic energy)
1 T 2

1 2 dx m( x) y 0 2
l
j
M
i 1
( x i , t )] i[y
2
1 cos 2 (t )[ 2
1 V 2
l

l 0
j
m( x) 2 ( x)dx
l 0

m 2 ( x)dx 2 mA 2 2
l 0
l 630
V max
1 2

EI [ ( x)] 2 dx EIA 2
4 5l 3
由式（6-11）可得 222.5 EI
l m
与精确解结果一致。
Page 18
6.1 瑞利法(Rayleigh method)：——连续体系
1 1 1 -1 1 [R][K] = 1 2 2 k 1 2 3
为求出系统的静位移，可以采用柔度矩阵：
Page 12
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第六章 结构振动特征值问题的矩阵摄动法§6.1 概述工程振动问题中经常遇到结构有小改动的情形，例如结构的制造误差、结构的小修改设计、对结构参数改变进行灵敏度分析等。

这些情况都有一个共同的特点，就是结构的参数仅发生很小的变化。

结构参数的小变化所引起的结构振动特性变化问题，对工程结构优化设计有重要意义。

经典的方法是每修改一次方案就需要求解一次结构的固有特性，即求解广义特征值问题。

这对于大型结构的振动分析，是非常麻烦的。

我们希望能找到一种能够利用修改前结构的固有特性信息，且计算量小的方法，来解决上述问题。

矩阵摄动法就是这种结构特征值重分析和灵敏度快速分析的计算方法。

§6.2 孤立特征值的摄动法对离散系统特征值问题，假定已经得到了其特征对的解：}]{[}]{[)(00)(0)(00i i i u M u K λ=（6－1）][],[00M K 分别为参数未变化的原结构刚度矩阵和质量矩阵，第i 个特征值2)(0)(0)(i i ωλ=，)(0i ω为第i 阶固有频率，}{)(0i u 为第i 阶特征向量（固有模态）。

结构参数的变化或修改设计一般通过刚度矩阵和质量矩阵的改变反映出来。

即][][][10M M M ε+= （6－2） ][][][10K K K ε+= （6－3）ε称为小参数。

先看）（i 0λ是单根的情形。

上标)(i 代表第i 个根，下标0)(代表参数未变化的原结构。

从物理意义上知道，绝大多数情况下，质量阵和刚度阵只有小变化时，特征值和特征向量也只有小量变化，根据摄动理论，特征值和特征向量按小参数ε展开为：+++=+++=)(22)(1)(0)()(22)(1)(0)(}{}{}{}{i i i i i i i i u u u u λεελλλεε （6－4）代入方程（6－1），略去)(2εO 以上的项，比较ε同次幂的系数，得到：}]{[}]{[)(00)(0)(00i i i u M u K λ= （6－5）}]{[}]{[}]{[}]{[}]{[)(00)(1)(01)(0)(10)(0)(01)(10i i i i i i i i u M u M u M u K u K λλλ++=+（6－6） }]{[}]{[}]{[}]{[}]{[}]{[}]{[)(00)(2)(01)(1)(10)(1)(11)(0)(20)(0)(11)(20i i i i i i i i i i i i u M u M u M u M u M u K u K λλλλλ++++=+（6－7））（i 1λ、）（i 2λ、}{)(1i u 、}{)(2i u 分别是特征值与特征向量的第一阶摄动和第二阶摄动。

因此，只要解出了原系统的特征值和特征向量，并知道了质量阵和刚度阵的改变量][1M 、][1K ，就可以求出特征值的摄动解。

【一阶摄动】由展开定理，∑==+++=ns s s i u c u c u c u c u 1)(0)1()3(0)1(3)2(0)1(2)1(0)1(1)(1}{}{}{}{}{ （6－8）代入(6－6)式}]{[}]{[}{][}]{[}{][)(00)(1)(01)(01)(0)1(0)(0011)(0)1(0i i i i ns s s i ins s s u M u M u c M u K u c K λλλ++=+⋅∑∑== （6－9）方程两边乘以Ts u }{)(0并利用正交性公式： isi Ts s is i T s u M u u K u δλδ==}]{[}{}]{[}{)(00)(0)(0)(00)(0 （6－10）得到：is i i T s i i s i T s s s u M u c u K u c δλλλλ)(1)(01)(0)(0)(0)1(01)(0)(0)1(}]{[}{}]{[}{++=+ （6－11）即：}]{[}{}]{[}{)()(01)(0)(001)(0)(1)(0)(0)1(i T s i i T s is i s i s u M u u K u c λδλλλ-=+- （6－12）当i s =时，)(0)(0s i λλ=，1=is δ}]{[}{}]{[}{)(01)(0)(0)(01)(0)(1i T i i i T i i u M u u K u λλ-= （6－13）当i s ≠时，0=is δ})]{[}{}]{[}({1)(01)(0)(0)(01)(0)(0)(0)1(i T s i i T s s i s u M u u K u c λλλ--=（6－14） 根据振型的正交性：1}]{[}{)()(=i T i u M u （6－15）将（6－4）式代入1}){}{}({])[]([}){}{}({)(22)(1)(010)(22)(1)(0=++⋅+++i i i T i i i u u u M M u u u εεεεε （6－16）展开并比较ε的同次幂项，有：1}]{[}{)(00)(0=i T i u M u（6－17）0}]{[}{}]{[}{}]{[}{)(01)(0)(00)(1)(10)(0=++i T i i T i i T i u M u u M u u M u （6－18） 0}]{[}{}]{[}{}]{[}{}]{[}{}]{[}{)(01)(1)(11)(0)(00)(2)(10)(1)(20)(0=++++i T i i Ti i T i i T i i T i u M u u M u u M u u M u u M u （6－19）用][}{0)(0M u Ti 前乘（6－8）式，根据正交性，有：}]{[}{)(10)(0)1(i T i i u M u c = （6－20）转置得到：}]{[}{)(00)(1)1(i T i i u M u c = （6－21）代入（6－18）式，得到：}]{[}{21)(01)(0)1(i T i i u M u c -= （6－22）所以，代入（6－8）式得：}}){]{[}({21}}){]{[}{}]{[}({1}{)(0)(01)(0)(0)(01)(0)(0)(01)(01)(0)(0)(1i i T i s i T s i i T s nis s s i i u u M u u u M u u K u u ---=∑≠=λλλ （6－23）故一阶摄动解为：}}){]{[}({21}}){]{[}{}]{[}({1}{}]{[}{}]{[}{)(0)(01)(0)(0)(01)(0)(0)(01)(01)(0)(0)(1)(01)(0)(0)(01)(0)(1i i T i s i T s i i T s nis s s i i i T i i i T i i u u M u u u M u u K u u u M u u K u ---=-=∑≠=λλλλλ（6－24） 【二阶摄动】同样根据展开定理：∑==ns s s i u c u 1)(0)2()(2}{}{ （6－25） 代入（6－7）式，得：}]{[}]{[}]{[}]{[}{][}]{[}{][)(00)(2)(01)(1)(10)(1)(11)(0)(01)2(0)(0)(11)(01)2(0i i i i i i i i s ns s i i s ns su M u M u M u M u c M u K u c K λλλλλ++++=+∑∑==（6－26）上式两端左乘T s u }{)(0，并利用正交性，得到：}]{[}{}]{[}{}]{[}{}]{[}{)()(01)(0)(1)(10)(0)(1)(11)(0)(0)(11)(0)(2)(0)(0)2(i T s i i T s i i T s i i T s is i s i s u M u u M u u M u u K u c λλλδλλλ---=+- （6－27）当i s =时，)(0)(0s i λλ=，1=is δ，特征值的二阶摄动解为：}]{[}{}]{[}{}]{[}{}]{[}{)(01)(0)(1)(10)(0)(1)(11)(0)(0)(11)(0)(2i T i i i T i i i T i i i T i i u M u u M u u M u u K u λλλλ---= （6－28）当i s ≠时，0=is δ})]{[}{}]{[}{}]{[}{}]{[}({1)(01)(0)(1)(10)(0)(1)(11)(0)(0)(11)(0)(0)(0)2(i T s i i T s i i Ts i i T s s i s u M u u M u u M u u K u c λλλλλ----=（6－29）当s i =时，)2(i c 的确定如下：以][}{0)(0M u Ti 乘∑==ns s s i u c u 1)(0)2()(2}{}{，根据正交性得到：}]{[}{)(20)(0)2(i T i i u M u c = （6－30）转置得：}]{[}{)(00)(2)2(i T i i u M u c = （6－31）代入到（6－18）式，得到：})]{[}{}]{[}{}]{[}({21)(01)(1)(11)(0)(10)(1)(i T i i T i i T i s i u M u u M u u M u c ++-=（6－32）故特征向量的二阶摄动解为：}}){]{[}{}]{[}{}]{[}({21}{})]{[}{}]{[}{}]{[}{}]{[}({1}{)(0)(01)(1)(11)(0)(10)(1)(0)(01)(0)(1)(10)(0)(1)(11)(0)(0)(11)(01)(0)(0)(2i i T i i T i i T i s i T s i i Ts i i T s i i T s nis s s i i u u M u u M u u M u u u M u u M u u M u u K u u ++-⋅----=∑≠=λλλλλ （6－33）§6.3 退化系统特征值的摄动当系统有重频时，称为退化系统。

退化系统特征值的摄动有两个特点。

即：参数变化后，原来的一组特征值由重特征值变为非重特征值；参数变化后，特征向量可能产生跳跃。

即)1,,1,(}{}{}{)(0)()(-++=-=m i i i j u u u j j j ∆（m 为重频数） （6－34）不再是一个小量。

下面以一个简单的例子来说明。

图示的两自由度系统，其运动方程为：()⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+----+++⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡0043)(43)(434002132323232121x x k k k k k k k k k x x m m （6－35）记：2ωλ=，则（i ） 当k k k k ===321m k2321==λλ ⎥⎦⎤⎢⎣⎡=1001][φ （6－36）（ii ） 当k k k k k k ==+=3211,δ⎥⎦⎤⎢⎣⎡==+=1001][23223211φλδλm kmk k （6－37） （iii ） 当k k k k k k ==+=2133,δ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-==+=21232321][23223231φλδλm kmk k （6－38） 由此看到，对退化系统，当参数有小的变化时，有时特征向量会发生突变的跳跃现象。