第22讲唯一性定理第4章介质中的电动力学2§2唯一性定理
- 格式:doc
- 大小:877.00 KB
- 文档页数:12


唯一性定理唯一性定理是数学中的重要定理之一,它指出了在某些条件下,特定类型的方程或问题只有唯一解。
唯一性定理最经典的形式是微分方程的唯一性定理,它在微积分和微分方程的研究中占据重要的地位。
微分方程是描述自然现象和物理规律的重要工具,通过对微分方程的求解,可以得到问题的解析解,从而更好地理解和预测现象。
然而,并不是所有的微分方程都能够得到解析解,有些方程可能只能通过数值方法进行求解。
因此,唯一性定理提供了一种重要的判据,用于确定方程是否有唯一解。
在微分方程的唯一性定理中,通常需要满足连续性和局部利普希茨条件。
连续性要求方程中的函数在某个区域内是连续的,这是非常基本的要求,因为连续性是数学分析中的重要概念。
局部利普希茨条件则要求方程中的函数在一定范围内具有有界的导数,这个条件保证了方程的解在某个区间内是唯一的。
微分方程的唯一性定理可以通过三个步骤来证明。
首先,需要利用泰勒级数展开将微分方程转化为一个无穷级数。
其次,需要证明无穷级数的解存在且唯一。
最后,通过局部利普希茨条件和连续性条件,得到解的存在范围。
除了微分方程的唯一性定理,数学中还有一些其他类型问题的唯一性定理。
例如,线性代数中的矩阵方程的唯一性定理,数论中的素因数分解的唯一性定理等等。
这些定理都有一个共同点,即在满足一定条件下,问题的解是唯一的。
唯一性定理在数学研究和应用中有着广泛的应用。
通过这些定理,我们可以确定问题是否存在唯一解,从而帮助我们深入研究和理解问题。
唯一性定理也经常被用于证明其他定理,深化了我们对数学的认识和理解。
总之,唯一性定理是数学中的一类重要定理,它指出了在满足特定条件下,方程或问题具有唯一解的情况。
微分方程的唯一性定理是其中最经典和重要的定理之一,它在微积分和微分方程的研究中扮演着重要的角色。
唯一性定理的应用广泛,帮助我们理解和解决各种数学问题,并进一步推动数学的发展。
唯一性定理除了在微分方程中应用广泛,还在其他数学领域中有重要的应用。



第22讲唯一性定理第4章介质中的电动力学2§2唯一性定理第22讲唯一性定理第4章介质中的电动力学(2)§4.2 唯一性定理在上节中我们说明静电学的基本问题是求出所有边界上满足边值关系或给定边界条件的泊松方程的解。
本节我们把这问题确切地表述出来,即需要给出哪一些条件,静电场的解才能唯一地被确定。
静电场的唯一性定理对于解决实际问题有着重要的意义。
因为它首先告诉我们,哪些因素可以完全确定静电场,这样在解决实际问题时就有所依据。
其次,对于许多实际问题,往往需要根据给定的条件作一定的分析,提出尝试解。
如果所提出的尝试解满足唯一性定理所要求的条件,它就是该问题的唯一正确的解。
下面我们先提出并证明一般形式的唯一定理,然后再证明有导体存在时的唯一性定理。
1. 静电问题的唯一性定理下面我们研究可以均匀分区的区域V ,即V 可以分为若干个均匀区域 V i ,每一个区域的电容率为ε i 。
设V 内有给定的电荷分布ρ(x )。
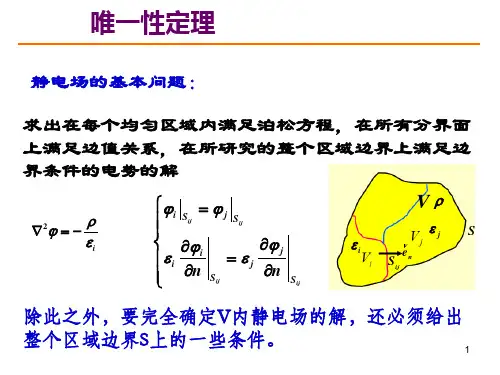
电势φ 在均匀区域 V i 内满足泊松方程2i ρε?=- (4.2---1)在两区域 V i 和 V j 的分界上满足边值关系()()i j i i j j nn εε=??= (4.2---2)泊松方程(4.2---1)式和边值关系(4.2---2)式是电势所必须满足的方程,它们属于电场的基本规律。
除此之外,要完全确定V 内的电场,还必须给出V 的边界S 上的一些条件。
下面提出的唯一性定理具体指出所需给定的边界条件。
唯一性定理:设区域V 内给定自由电荷分布,在V 的边界上S 上给定(1)电势φ| s 或(2)电势的法向导数?φ/?n | s ,则V 内的电场唯一确定。
也就是说,在V 内存在唯一的解,它在每个均匀区域内满足泊松方程(4.2---1),在两均匀区域分界面上满足边值关系,并在V 的边界S 上满足该给定的φ或?φ/?n 值。
证明设有两组不同的解φ' 和φ'' 满足唯一性条件定理的条件。





唯一性定理的内容及其意义唯一性定理是一个重要的数学定理,它的内容和意义一直都受到人们的认可与推崇。
它的内容可以简单地总结如下:如果一个非空集合中的任意一组子集的联合也是一个非空的集合,那么这个非空集合的最小元素就是该集合中的唯一性最小元素。
首先,为了更加清楚地理解唯一性定理,我们需要搞清楚一些基本概念。
首先,什么是非空集合?简单来说,一个非空集合就是一组非空的元素,这些元素可以是数字、汉字、日期等等,存在于一起,有一定的逻辑关系。
其次,什么是子集?子集是指一个集合中的子集,子集中包含的元素不一定都在原始集合中。
最后,什么是联合?联合就是把多个集合的元素合并起来的一个新的集合。
接下来,让我们继续讨论唯一性定理的内容及其意义。
首先,唯一性定理满足一定的条件,即一个非空集合中的任意一组子集的联合也是一个非空的集合。
然后,唯一性定理指出,在这种情况下,该集合中的唯一性最小元素就是该集合中的最小元素。
有了这个定理,我们可以用它来推断一些实际的问题,比如,在一组数据中,如果想知道某一类数据的最小值,可以使用这个定理来推断出这一类的最小值。
总结起来,唯一性定理乃至数学定理的内容,就是只要满足一定的条件,就可以推断出一组数据中某一类数据的最小值。
唯一性定理的意义也是重要的,它可以帮助我们更好地理解一组数据,从而有效地管理和使用这些数据,这对于现代社会来说都是非常有用的。
此外,唯一性定理在某种程度上也引导了现代数学的发展,比如,如果没有唯一性定理,可能就没有拉格朗日提出的方程组的概念,更不用说今天的方程组研究了。
以上就是唯一性定理的内容及其意义。
总结起来,唯一性定理是一个重要的数学定理,它满足一定条件时,可以推断出一组数据中某一类数据的最小值。
它的意义在于有助于我们更好地理解一组数据,从而更有效地管理和使用这些数据,以及引导了现代数学的发展。
唯一性定理蒋文佼(080320124)宋宝璋(080320125)夏世宇 (080320126) 李宝平 (080320127) 章文显 (080320129) 常 悦 (080320130) 1、试用唯一性定理证明:封闭导体壳内部的电场不受壳外电荷(包括壳外表面)的影响。
证:导体壳无论是用电势还是用总电量给定,壳的内外一般存在着四部分电荷。
如图所示,壳内外的电荷分布分别为 ρ 和 ρe ,壳内、外表面1S 、2S 上各自的面电荷分布为σ 和 σe 。
壳内外的场是这四部分电荷共同激发的。
根据定理,首先写出壳内空间电势应满足的条件:(一) 2ρϕε∇=- ,ρ 为壳内电荷分布。
(二)壳内表面1S 上的边界条件是:2S 上的总电量 1s dS q σ=-⎰ (1)其中 Vq dV ρ=⎰ 是壳内的总电量,V 是壳内区域的体积。
在壳层内作一高斯面 0S 后(如图中虚线所示),用高斯定理很容易证明(1)成立。
因此在给定 ρ 布后, 1S 上边界条件也已经给定为 q - ,和导体壳本身是有电势还是用总电量给定无关。
根据唯一性定理,满足(一)、(二)的ϕ 就是解。
由于(一)e和(二)与壳外的ρe 和 σρ 的电势并不唯一,可以差一个常数。
当然当壳用电势 0φ 给定时,1S 上的边界条件就是10|S ϕφ= 。
所以壳内不但电场唯一,而且电势也是唯一。
2.如图,有一电势为0φ的导体球壳,球心有一点电荷q ,球壳内外半径分别为2R 和1R 。
试用唯一性定理: (一)判断0R φ是否球壳外空间的电势分布。
(二)求球壳内空间的电势分布解:(一)首先必须找出球内外电势应满足的条件,他们是:(a )20∇ϕ=(b )球壳外表面1S 上的边界条件,10s ϕ=φ (c )无穷远边界条件,0R →∞ϕ→若R φ是解,根据唯一性定理,它必须满足以上三个条件。
下面来检验:220010R Rφ∇=φ∇= (0),R ≠ 方程已满足。
第22讲 唯一性定理 第4章 介质中的电动力学(2)§4.2 唯一性定理在上节中我们说明静电学的基本问题是求出所有边界上满足边值关系或给定边界条件的泊松方程的解。
本节我们把这问题确切地表述出来,即需要给出哪一些条件,静电场的解才能唯一地被确定。
静电场的唯一性定理对于解决实际问题有着重要的意义。
因为它首先告诉我们,哪些因素可以完全确定静电场,这样在解决实际问题时就有所依据。
其次,对于许多实际问题,往往需要根据给定的条件作一定的分析,提出尝试解。
如果所提出的尝试解满足唯一性定理所要求的条件,它就是该问题的唯一正确的解。
下面我们先提出并证明一般形式的唯一定理,然后再证明有导体存在时的唯一性定理。
1. 静电问题的唯一性定理 下面我们研究可以均匀分区的区域V ,即V 可以分为若干个均匀区域 V i ,每一个区域的电容率为 ε i 。
设V 内有给定的电荷分布 ρ(x )。
电势 φ 在均匀区域 V i 内满足泊松方程 2i ρϕε∇=- (4.2---1)在两区域 V i 和 V j 的分界上满足边值关系()()i j i i j j nn ϕϕϕϕεε=⎧⎪∂∂⎨=⎪∂∂⎩ (4.2---2)泊松方程(4.2---1)式和边值关系(4.2---2)式是电势所必须满足的方程,它们属于电场的基本规律。
除此之外,要完全确定V 内的电场,还必须给出V 的边界S 上的一些条件。
下面提出的唯一性定理具体指出所需给定的边界条件。
唯一性定理: 设区域V 内给定自由电荷分布,在V 的边界上S 上给定 (1)电势φ| s 或(2)电势的法向导数 ∂φ/∂n | s ,则V 内的电场唯一确定。
也就是说,在V 内存在唯一的解,它在每个均匀区域内满足泊松方程(4.2---1),在两均匀区域分界面上满足边值关系,并在V 的边界S 上满足该给定的φ或∂φ/∂n 值。
证明 设有两组不同的解 φ' 和 φ'' 满足唯一性条件定理的条件。
令,ϕϕϕ'''=- (4.2---3) 则由 ▽2φ' = −ρ/εi ,▽2φ'' = −ρ/εi ,得20ϕ∇= (在每个均匀区V i 内) (4.2---4) 在两均匀区界面上有i j ϕϕ= ()()i i j j n nϕϕεε∂∂=∂∂ (4.2---5)在整个区域V 的边界S 上有 0SS S ϕϕϕ'''=-= (4.2---6a )或SSSnnnϕϕϕ'''∂∂∂=-∂∂∂=0 (4.2---6b )考虑第i 个均匀区 V i 的界面 S i 上的积分iiS d εϕϕ∇⋅⎰ÑS由附录(Ⅰ.7)式,这积分可以变换为体积分()iiii S V d dV εϕϕεϕϕ∇⋅=∇⋅∇⎰⎰ÑS22()iii i V V dV dV εϕϕεϕ=∇+∇⎰⎰由(4.2---4)式,右边最后一项为零,因此2()iii i S V d dV Ñεϕϕεϕ∇⋅=∇⎰⎰S 对所有分区 V i 求和得2()iiii S V iid dV εϕϕεϕ∇⋅=∇∑∑⎰⎰ÑS (4.2---7)在两均匀区 V i 和 V j 的界面上,由(4.2---5)式,φ 和ε▽φ的法向分量分别相等,但 d S i = −d S j 。
因此,在(4.2---7)式左边的和式中,内部分界面的积分互相抵消,因而只剩下整个V 的边界S 上的积分。
但在S 上,由(4.2---6)式,或者 φ| s ,或者 ∂φ/∂n | s ,两情形下面积分都等于零。
因此由(4.2---7)式有2()0ii V idV εϕ∇=∑⎰由于被积分函数 ε(▽φ)2 ≥0,上式成立的条件是在V 内各点上都有 0ϕ∇= 即在V 内ϕ=常量由(4.2---3)式, φ' 和 φ'' 至多只能相差一个常量。
但电势的附加常量对电场没有影响,这就证明了唯一性定理。
2. 有导体存在时的唯一性定理 当有导体存在时,由实践经验我们知道,为了确定电场,所需条件有两种类型:一类是给定每个导体上的电势 φi ,另一个是给定每个导体上的总电荷 Q i 。
为简单起见,我们只讨论区域内含一种均匀介质的情形。
如图2-3,设在某区域V 内有一些导体,我们把除去导体内部以后的区域称为V ' ,因而V ' 的边界包括界面S 以及每个导体的表面 S i 。
设V ' 内有给定电荷分布 ρ ,S 上给定 φ| s 或 ∂φ/∂n | s 值。
对上述第一种类型的问题,每个导体上的电势 φi 亦给定,即给出了V ' 所有边界上的φ或 ∂φ/∂n 值,因而由上一小节证明了的唯一性定理可知,V ' 内的电场唯一地被确定。
对于第二种类型的问题,唯一性定理表述如下:设区域V 内由一些导体,给定导体之外的电荷分布ρ,给定各导体上的总电荷 Q i 以及V 的边界S 上的φ或 ∂φ/∂n 值,则V 内的电场唯一确定。
也就是说,存在唯一的解,它在导体以外满足泊松方程2/ϕρε∇=- (4.2---8) 在第i 个导体上满足总电荷条件(4.2---9) i i S Q dS n ϕε∂-=∂⎰Ñ (4.2---9)(n 为导体面的外法线)和等势面条件 iS i ϕϕ==常量, (4.2---10)以及在V 的边界 S 上具有给定的 φ| s 或 ∂φ/∂n | s 值。
证明 设有两个解φ'和φ" 满足上述条件,令 ,ϕϕϕ'''=- 则φ满足20,ϕ∇=(V '体内) (4.2---11) 0,i S dS nϕ∂-=∂⎰Ñ iS ϕ=常量 (4.2---12)S ϕ=0或Snϕ∂∂=0 (4.2---13)对区域 V ' 用公式()V d dV ϕϕϕϕ'∇⋅=∇⋅∇⎰⎰ÑS22''()V V dV dV ϕϕϕ=∇+∇⎰⎰ (4.2---14)上式左边的面积分包括V 的边界S 以及每个导体的表面 S i 上的积分。
作为 V ' 的边界, S i 的法线指向导体内部。
若我们用n 表示导体向外的法线分量,由(4.2---12)式,在 S i 上的积分为0ii i S S d dS nϕϕϕϕ∂∇⋅=-=∂⎰⎰蜒S 由(4.2---13)式,在S 上的面积分亦为零。
因而(4.2---14)式左边等于零。
该式右边最后一项由(4.2---11)式得零,因此, 2()0dV ϕ∇=⎰ 由此得0ϕ∇=即φ'和φ" 至多只能相差一个常量,因而电场唯一确定。
当导体外的电势确定后,由边值关系 iS nϕεσ∂-=∂ (4.2---15)因而导体上的电荷面密度亦同时确定。
由本定理的证明可以看出电场与电荷的相互制约关系。
若空间内有一些导体,给定各导体上的总电荷后,在空间中就激发了电场。
同时导体上的电荷受到电场作用。
在静止情况,导体上的电荷分布使得导体表面为一个等势面。
因此,由导体上的总电荷和导体面为等势面的条件同时确定空间中的电场以及导体上的电荷面密度。
例 如图2-4,两同心导体球壳之间充以两种介质,左半部电容率为 ε1,右半部电容率为 ε2。
设内球壳带总电荷Q ,外球壳接地,求电场和球壳上的电荷分布。
解 设两介质内的电势、电场强度和电位移分别为 φ1, E 1,D 1 和 φ2 ,E 2,D 2。
由于左右两半是不同介质,因此电场一般不同于只有一种均匀介质时的球对称解。
在找尝试解时,我们先考虑两介质分界面上的边值关系21,t t E E = (4.2---16) 21,n n D D = (4.2---17) 如果我们假设E 仍保持球对称性,即 13Ar =r E ,(左半部) 23Ar=r E ,(右半部) (4.2---18) (A 为待定常数),则在分界面两侧电场与界面相切,并有相同数值。
因而边值关系(4.2---16)得到满足。
而且由于 D 2n = D 1n = 0 ,因而(4.2---17)式亦被满足。
球对称的E 再到体面上处处与球面垂直,因而保证导体球面为等势面。
为了满足内导体总电荷等于Q 的条件,我们计算内导体球面上的积分121122,S S d d d εε⋅=⋅+⋅=⎰⎰⎰ÑD S E S E S Q (4.2---19)其中 S 1和 S 2 分别为左右半球面。
把(4.2---18)式代入得 122().A Q πεε+= 解得122()A πεε=+Q代入(4.2---18)式得 1312,2()rπεε=+QrE (左半部) 2312.2()r πεε=+QrE (右半部) (4.2---20)此解满足唯一性定理的所有条件,因此是唯一正确的解。
虽然 E 仍保持球对称性,但是D 和导体上的电荷面密度σ不具有球对称性。
设内导体球半径为a ,则球面上的电荷面密度为 11111212,2()r r D E a εσεπεε===+Q(左半部)22222212.2()r r r D E aεσεπεε===+Q(右半部) 注意导体两半球上的面电荷密度是不同的,但E 却保持球对称性。
读者试解释这一点。
第21讲 习题解答:第35-36页,第7,8,9,11,12,13题。
7.有一内外半径分别为1r 和2r 的空心介质球,介质的介电常数为ε使介质内均匀带静止自由点荷f ρ求:(1) 空间各点的电场(2) 极化体电荷和极化面电荷分布解:(1)在1r 内取同心球面,以r (1r r <)为半径 ∵D ρ∇⋅=u u v∴0SD d σ⋅=⎰⎰u u vu u vÒ ∴0D E ==u v u u v在12r r r <<内取同心球面r ,233144()3f D d E r r r σεππρ⋅=⋅=-⎰⎰u u vu u v Ò ∴3313()3f r r E r r ρε-=u u vuv 在2r r >取同心球:23302144()3f D d S E r r r εππρ⋅=⋅=-⎰⎰u u v u vÒ∴333210()/3f E r r r r ρε=-u u v u v方向:f ρ为正,均为圆心射线方向,f ρ为负,均为汇聚圆心方向(2)∴0000()(1)p f f p E D χεχεερχερρεεε=-∇⋅=-∇⋅=-∇⋅=-=-u vu u vu u v ∴1r r <或2r r >处是真空 ∴0p ρ= 在12r r r << 0(1)p f ερρε=- ∴1100p r r Eσε=== (1r r =)2332122200))()3((f r r p r r rEσρεεεεε==-=--3302122(1)3f r r r ερε-=- 2122211223333002121444440()(1)()(1)033r p p P r f f r r r drr r r r πσπσρπεεπρπρεε++=+--+--=⎰即,介质的总极化电荷为零。