静磁场唯一性定理的证明

静磁场中的唯一性定理作者：戴振翔郑赣鸿张青等来源：《赤峰学院学报·自然科学版》 2014年第14期戴振翔，郑赣鸿，张青，马永青（安徽大学物理与材料科学学院，安徽合肥 230039）摘要：唯一性定理是解决静电磁场问题的重要理论依据，应用构造恰当函数的技巧和一些数学运算，从给定的边界条件出发，本文给出了静磁场唯一性定理的证明，最后给出了唯一性定理关于静磁场实际问题的应用举例.关键词：电动力学；唯一性定定理；边界条件中图分类号：O442 文献标识码：A 文章编号：1673-260X（2014）07-0022-02静电场和静磁场中的唯一性定理是电动力学中的重要定理.静电场的唯一性定理在郭硕鸿的《电动力学》已经给出非常清晰的证明.然而，关于静磁场中的唯一性定理，却没有给出.因此，有必要对静电场和静磁场的唯一性定理给出一个统一的系统证明，为解决静场问题提供理论依据.1 静磁场边界条件对于存在有限边界的静磁场问题，边界条件一般只有一种选择，那就是给定边界上的磁感应强度的法向分量：即通过边界的净磁通为零.2 静磁场唯一性定理的证明任意两个相邻的介质分界面上满足边值关系：即A1和A2相差一个常数，两者所确定的磁感应强度矢量相同，即磁场唯一确定.由以上的论证，可以得到不随时间变化的矢量场，在给定的边界条件和其满足的可以完备描述其不含时的矢量场下，是唯一确定的.3 结论从静场的角度论证电动力学中的唯一性定理业已完成.在时变电磁场中论证唯一性定理和在运动的参考系下即相对论情形下论证电磁张量的特定给定的边界条件下的唯一性定理是今后进一步的研究工作.参考文献：〔1〕蔡圣善，朱耘.经典电动力学[M].上海：复旦大学出版社，1985.120-210.〔2〕赵凯华，陈熙谋.电磁学上册[M].北京：高等教育出版社，1985.213-219.〔3〕胡友秋，程福臻.电磁学与电动力学上册[M].北京：科学出版社，2008.30-85.〔4〕张玉民，戚伯云.电磁学[M].北京：科学出版社2007.213-241.〔5〕郭硕鸿，电动力学[M].北京：高等教育出版社，2008.37-90.〔6〕林璇英，张之翔.电动力学题解[M].北京：科学出版社，2007.99-263.〔7〕梁昌洪，褚庆昕.运动边界的电磁场边界条件[J].物理学报，2002,51(10)：2201-2204(10).〔8〕雷银照，徐纪安.时变电磁场唯一性定理的完整表述[J].电工技术报，2000,15(1)：16-20.〔9〕胡森.静磁场矢势A的唯一性定理及其证明[J].湖北第二师范学院学报，2008,25(2)：31-32.〔10〕张福恒.静电唯一性定理的意义与应用[J].海南师范大学学报，2008,21(2)：161-166.〔11〕张国文，王福谦.在电磁学中讲授静电场的唯一性定理[J].长治学院学报，2005,22(2)：45-47.〔12〕邵建军.论电磁势的唯一性（非动力物理效应）与相对论[J].湖北教育学院学报，2002,19(2)：22-26.。

静磁场矢势→A的唯一性定理及证明
胡森
【期刊名称】《湖北第二师范学院学报》
【年(卷),期】2008(25)2
【摘要】唯一性定理是解决静电磁场问题的理论依据.课本中给出了静电场唯一性定理的表述形式及其严格证明,对于磁场部分则是点到即止.本文首先给出静磁场唯一性定理的表述形式,对一般情况下和库仑规范条件▽·→A=0下的情况均作了证明,得出后者只是一般情况下的一个特例.
【总页数】2页(P31-32)
【作者】胡森
【作者单位】湖北第二师范学院,物理与电子工程系,武汉,430205
【正文语种】中文
【中图分类】O44
【相关文献】
1.静磁场唯一性定理 [J], 宋福;罗世彬
2.再论静磁场唯一性定理 [J], 董钫
3.静磁场中的唯一性定理 [J], 戴振翔;郑赣鸿;张青;马永青
4.几个最优映射存在唯一性定理的统一证明 [J], 陈平
5.静电场电位边值问题唯一性定理的补充与完整证明 [J], 陈文卿;闫述
因版权原因，仅展示原文概要，查看原文内容请购买。

静电场唯一性定理
静电场唯一性定理是一种重要的物理定理，它有助于我们理解电场，研究电磁场，有助于研究一般相对论、量子力学和统计物理等科学理论的发展。

它指出，当电场的空间和时间的变化都可以完全确定时，其静态状态就是唯一的。

在实际应用中，它为解决复杂的电力电子、光电子和微电子学问题提供了有力的理论支持。

静电场唯一性定理是由19世纪90年代著名物理学家雷诺兹等提出的。

他们提出，电场的动量和能量有相应的定律，可以用来描述其变化，不论是在空间上还是时间上都是这样。

根据它们提出的新定律，假设电场的状态完全确定，不论是在空间上还是时间上，其静态状态都是唯一的。

结合泰勒到的变分原理，可以证明静电场唯一性定理的有效性。

当电场的状态完全确定时，可以用变分原理来证明它的静态态一定是唯一的，这就是静电场唯一性定理的关键性证明过程。

除了可以用于研究电场外，静电场唯一性定理也可以用于研究重力场。

由于重力场是空间和时间变量关系的最简单形式，可以用静电场唯一性定理来分析它，并且可以证明重力场也是唯一的。

总之，静电场唯一性定理是一种重要的物理定理，它对研究电场、重力场以及一般相对论、量子力学和统计物理等科学理论都有着重要的意义。

通过它，我们可以更加有效率地研究和分析物理现象，从而不断地拓展物理知识面，并进一步深入地研究物理本质。

- 1 -。

关于静电场中唯一性定理的证明
静电场中唯一性定理：满足静电场的**Maxwell方程组的唯一解，取决于指定的边界条件而不受初始条件的约束。

为了证明该定理，我们首先考虑Maxwell方程组：
$\nabla\cdot\vec{E} = \frac{\rho}{\varepsilon_0}$
可以看出，这套方程是由边界条件决定的，其解也是由边界条件决定的。

为证明唯一性定理，我们使用变分法从而得出以下**Euler-Lagrange方程组：
$\frac{\partial L}{\partial \vec{E}}-\frac{\partial}{\partial
\vec{x}}\frac{\partial L}{\partial(\frac{\partial\vec{E}}{\partial
x})}+\frac{\partial}{\partial t}\frac{\partial L}{\partial\frac{\partial
\vec{E}}{\partial t}}=0$
其中，$L$表示Lagrange函数，它是由Maxwell方程组构成的。

由此，我们可以得出雅可比方程：
这组方程有两个基本性质，一是称为“唯一性原理”，一是称为“不变性定理”。

不变性定理：对于给定的满足Maxwell方程组的特定边界条件，解不会随着时间变化而变化。

这两个定理说明，解是唯一的，而且不受初始条件的限制，而只受边界条件的约束。

因此，以上证明了静电场中唯一性定理。

静磁场唯一性定理的证明标量场的问题，情况与静电场完全相同。

讨论用磁矢量位描述的磁场问题。

设场域内有电流密度J ，讨论在什么边界条件下，旋度旋度方程J A μ=⨯∇⨯∇的解是唯一的。

证明：反证法。

假定在相同边界条件下有两个磁矢量位1A 和2A ，它们确定了1B 和2B11A B ⨯∇=、 22A B ⨯∇=它们的差值 21A A F -= 应满足V F ∈=⨯∇⨯∇0对于恒等式 ()()()()Q P P Q Q P ⨯∇⨯∇⋅-⨯∇⋅⨯∇=⨯∇⨯⋅∇ 运用高斯散度定理有dS n Q P dV Q P P Q SV ⋅⨯∇⨯=⨯∇⨯∇⋅-⨯∇⋅⨯∇⎰⎰)()( 令 F Q P ==，代入上式应有dS F F n dS F F n dS n F F dV F SS S V ⋅⨯∇⨯-=⨯∇⋅⨯=⋅⨯∇⨯=⨯∇⎰⎰⎰⎰)()()()(2 上式若要使体积分为零，必须是0=⨯∇F这可能是0=F ，即21A A =，或者是o A A ϕ∇±=21可以采取措施来进行必要处理，以使磁矢量位的解答唯一。

可分三种情况讨论(1) 边界面上给定第一类边界条件o A A =，则边界上有0=F ，面积分必为零，则21A A =，解答唯一；(2) 边界面上给定A n ⨯∇⨯，应有0=⨯∇⨯F n ，所以21A n A n ⨯∇⨯=⨯∇⨯这也能使积分方程的面积分项为零，进而使21A A =解唯一。

而条件A n ⨯∇⨯，其大小等于tB ，方向由B n ⨯确定。

可见在S 面上给定了t B ，即n A ∂∂ ——第二类边界条件，或给定了t H ，即nA ∂∂ μ1——仍是第二类边界条件，场域中的A的解唯一。

(3) 在边界上给定A n ⨯，有21A n A n⨯=⨯也可以使面积分项为零。

而A n ⨯的大小即为t A ，方向由A n ⨯确定。

即正确给定边界上A n ⨯，则V 域中A 有唯一解。

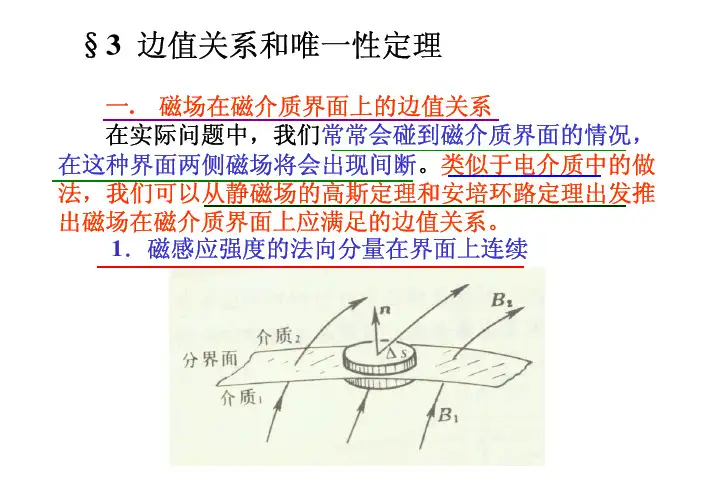
5ξ电磁场的边值关系一．引言当介质分布均匀时，出现了界面，→D ,→B 有跃变，界面两侧场值的关系 1.边值关系：描述介质界面两侧的场矢量与界面上电荷，电流的关系 2.麦氏方程组的微分形式要求→E ,→D ,→B ,→H 在介质中连续麦氏方程组的积分形式在场量不连续时不成立。

故不能用微分形式导出边值关系，而用积分形式讨论边值关系。

⎪⎪⎪⎭⎪⎪⎪⎬⎫=∙=∙⎰⎰⎰→→→→s s v S d B dv S d D 0ρ⇒导出法向关系⎪⎪⎪⎭⎪⎪⎪⎬⎫∙∂∂+∙=∙∙∂∂-=∙⎰⎰⎰⎰⎰→→→→→→→→→→s s l l S d t DS d j l d H S d tB l d E ⇒导出切向关系二．边值关系（法向关系证明从略,切向关系讲一例后推论） 1.→D 的法向有跃变⎰⎰=∙→→vsdv S d D ρ⇒σfD D n =-∙→→→)(12 （1）推论：εσσρρε0120)()(1pf v pf sE E n dv S d E +=-∙⇒+=∙→→→→→⎰⎰ （2）dv S d P ps⎰⎰-=∙→→ρ→⇒n )(12→→-∙P P =-σP（3）2．→B 的法向连续0)(0)(0112212=-∙−−−−→−=-∙⇒=∙→→→→→→→→⎰H u H u B B n n S d B s线性各向同性(4) 3.的→E 切向连续→→→→∙-=∙⎰⎰S d B dt d l d E s l 0)(12=-⨯⇒→→→E E n E Et t12= (5)4.的切向跃变→H→→→→→→→→→→=-⨯⇒∙∂∂+∙=∙⎰⎰⎰αf sflH H jn s d t DS d l d H )(12 （6）0)(012=-⨯=→→→→H H n f时，αH Ht t12= (7)线性各向同性：uB uBtt 1122=（8）推论：→→→→→→→→=-⨯⇒∙=∙⎰⎰αm s Ml M M jn S d l d M )(12 (9)5.→jf的法向跃变⎰⎰-=∙→→dv dt dS d sfjρtn f f f jj ∂∂-=-∙⇒→→→σ)(12 （10）0=∂∂t时，0)(12=-∙→→→jj f f n （11）三．说明1.上述关系在介质界面静止时导出，运动时，D ,B 法向关系仍成立，但E ,H 切向改变2.规定：界面法向n 从介质1指向介质2，否则差一负号3.具普遍意义：对任意矢量场，只要场方程与麦式方程组形式相同，其边值关系亦相同。