投影法及三视图
- 格式:ppt
- 大小:2.52 MB
- 文档页数:57



2投影法和三视图2.1体的三视图及其投影规律2.1.1常用的投影方法在工程上常用各种投影方法绘制工程图,常用投影方法有中心投影法、平行投影法。
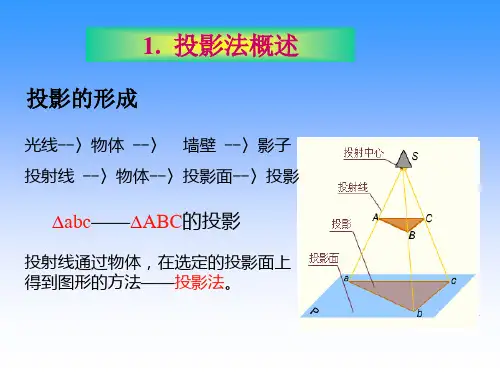
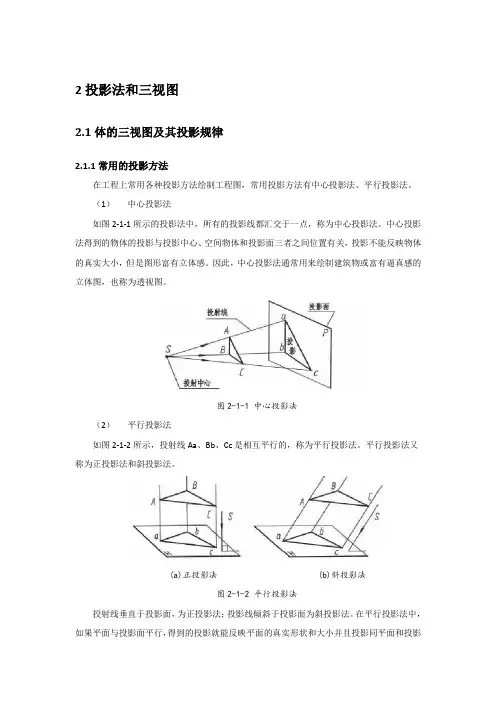
(1)中心投影法如图2-1-1所示的投影法中,所有的投影线都汇交于一点,称为中心投影法。
中心投影法得到的物体的投影与投影中心、空间物体和投影面三者之间位置有关,投影不能反映物体的真实大小,但是图形富有立体感。
因此,中心投影法通常用来绘制建筑物或富有逼真感的立体图,也称为透视图。
图2-1-1 中心投影法(2)平行投影法如图2-1-2所示,投射线Aa、Bb、Cc是相互平行的,称为平行投影法。
平行投影法又称为正投影法和斜投影法。
(a)正投影法 (b)斜投影法图2-1-2 平行投影法投射线垂直于投影面,为正投影法;投影线倾斜于投影面为斜投影法。
在平行投影法中,如果平面与投影面平行,得到的投影就能反映平面的真实形状和大小并且投影同平面和投影面的距离无关。
2.1.2投影规律在机械图中常用正投影法,它具有以下规律:1.真实性:当空间物体平行于投影面时,投影反映空间物体的实形。
2.积聚性:当空间物体垂直于投影面时,投影积聚为直线和点。
3.类似性:当空间物体倾斜于投影面时,投影与原图形类似。
2.2点的投影特性点是组成形体的最基本的几何要素。
2.2.1点的单面投影(如图2-2-1所示)设定投影面P,由一个空间点A做垂直于P面的投影线,相交于P面上一点a,点a就是空间点A在P面上的投影。
由此可见:一个空间点在一个投影面上有唯一确定的投影。
反之,如果已知点A在投影面P上的投影a,不能唯一地确定该点的空间位置,这是由于在从点A所做的P面的垂直线上所有各点的投影都位于a处。
图2-2-1 点的单面投影由于单面投影不能够确定点的唯一位置,所以在工程上常把几何体想象成放在相互垂直的两个或两个以上投影面间,在投影面上形成的投影就是多面正投影。
2.2.2点的两面投影(1)两投影面体系的建立相互垂直的正投影面V和水平投影面H它们相交投影轴OX,便组成了V、H投影面体系。
2-1 投影法与三视图物体在光线照射下,在地面或墙壁上产生影子。
人们对这种自然现象加以抽象研究,总结其中规律,创造了投影法。
所谓投影法,就是投射线通过物体,向选定的平面(投影面)投影,并在该平面上得到图形(投影图)的方法。
投影法分为两大类:中心投影法和平行投影法。
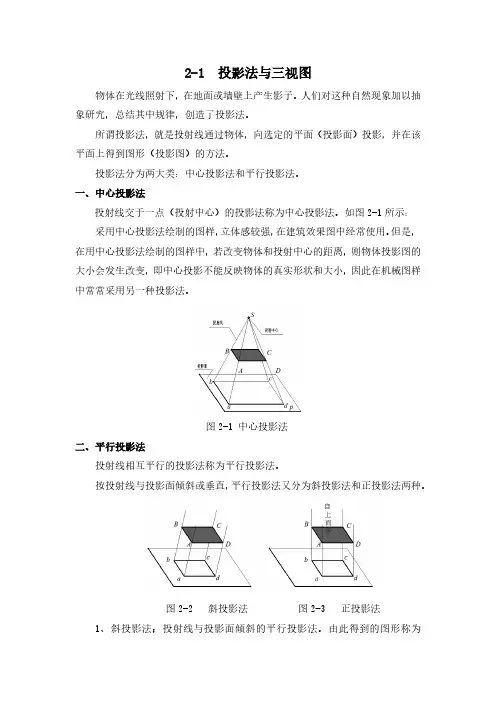
一、中心投影法投射线交于一点(投射中心)的投影法称为中心投影法。
如图2-1所示:采用中心投影法绘制的图样,立体感较强,在建筑效果图中经常使用。
但是,在用中心投影法绘制的图样中,若改变物体和投射中心的距离,则物体投影图的大小会发生改变,即中心投影不能反映物体的真实形状和大小,因此在机械图样中常常采用另一种投影法。
图2-1 中心投影法二、平行投影法投射线相互平行的投影法称为平行投影法。
按投射线与投影面倾斜或垂直,平行投影法又分为斜投影法和正投影法两种。
图2-2 斜投影法图2-3 正投影法1、斜投影法:投射线与投影面倾斜的平行投影法。
由此得到的图形称为斜投影图(简称斜投影)。
如图2-2所示。
2、正投影法:投射线与投影面垂直的平行投影法。
由此得到的图形称为正投影图(简称正投影)。
如图2-3所示。
正投影图度量性好,作图简单,机械图样常常采用正投影法绘制。
三、正投影的基本特性(单投影面)1、真实性:当物体上的平面(或直线)与投影面平行时,其投影反映实形(或实长)。
如图2-4(a)。
2、积聚性:当物体上的平面(或直线)与投影面垂直时,其投影积聚成直线(或点)。
如图2-4(b)。
3、类似性(亦称收缩性):当物体上的平面(或直线)与投影面倾斜时,其投影收缩成原来形状的类似形。
如图2-4(c)。
图2-4 正投影的特性四、三视图的形成及投影规律1、三投影面体系一般情况下,物体的一个投影图(二维)不能准确地反映物体(三维)的完整形状,如图2-5所示。
要想准确表达物体的结构形状,就必须增加投影图。
工程上常采用在三投影面体系中得到的三面投影图来表达物体的形状,如图2-6所示。