当前位置：文档之家 › 广技师材料力学-压杆稳定

广技师材料力学-压杆稳定

  • 格式：doc
  • 大小：262.50 KB
  • 文档页数：5

下载文档原格式

  / 5

合集下载

材料力学-09压杆稳定

材料力学-09压杆稳定
其它支承情况下，压杆临界力的欧拉公式
EI Fcr 2 ( L)
2
压杆临界力欧拉公式的一般形式
—长度系数（或约束系数）。
表10–1 各种支承约束条件下等截面细长压杆临界力的欧拉公 式 两端固定但可沿 支承情况 两端铰支 一端固定 两端固定 一端固定 横向相对移动 另端铰支 另端自由
Fcr
Fcr A cr 2 8.367 10 4 181 .7 10 6 304 kN
安全因数
Fcr 304 n 2.02 P 150
§9–5
压杆的稳定条件:
压杆的稳定校核
Fcr n nst F
n
--压杆工作安全因数
nst --稳定安全因数
例1
空气压缩机的活塞杆由45钢制成，s 350MPa, p 280MPa,
例1 柴油机的挺杆是钢制空心圆管，外径和内径分别为12mm 和10mm，杆长383mm，钢材的E=210MPa.已知挺杆工作时的最 大压力为F=2290N，规定的稳定安全因数为nst=3-5。试校核 挺杆的稳定性 解：挺杆横截面的惯性矩是
I

64
(D d )
4 4

64
(0.012 4 0.014 ) 5.26 10 10 m 4
M P
yccoskxd sinkx
边界条件为:
M0
P P
M0
x0, y y0;xL, y y0
M c ,d 0,k L2n 并 k Ln P
kL2n
为求最小临界力，“k”应取除零以外的最小值，即取：
kL2
所以，临界力为：
4 2 EI 2 EI Pcr 2 L ( L / 2) 2

材料力学第9章 压杆稳定

材料力学第9章 压杆稳定

第9章 压杆稳定 图9－6
第9章 压杆稳定
9.2.3 两端非铰支细长压杆的临界载荷 1.一端固定一端自由的细长压杆的临界载荷 图9－7所示为一端固定、一端自由的长为l的细长压杆。
当轴向压力F=Fcr时，该杆的挠曲轴与长为2l的两端铰支细 长压杆的挠曲轴的一半完全相同。因此，如果二杆各截面的 弯曲刚度相同，则临界载荷也相同。所以，一端固定一端自 由、长为l的细长压杆的临界载荷为
第9章 压杆稳定
9.2.2 大挠度理论与实际压杆 式（9－1）与式（9－2）是对于理想压杆根据小挠度挠
曲轴近似微分方程得到的。如果采用大挠度挠曲轴的微分方
程 ddx1xM ExI进行理论分析，则轴向压力F与压杆最
大挠度wmax之间存在着如图9－6中的曲线AB所示的确定关 系，其中A点为曲线的极值点，相应之载荷Fcr即为上述欧拉 临界载荷。
Fcr
2 EI
2l 2
（9－3）
第9章 压杆稳定
图9－7
第9章 压杆稳定
2.两端固定的细长压杆的临界载荷 图9－8所示为两端固定的长为l的细长压杆，当轴向压 力F=Fcr时，该杆的挠曲轴如图9－8(a)所示，在离两固定端 各l/4处的截面A、B存在拐点，A、B截面的弯矩均为零。因 此，长为l/2的AB段的两端仅承受轴向压力Fcr（见图9－8 (b)），受力情况与长为l/2的两端铰支压杆相同。所以，两 端固定的压杆的临界载荷为
Fcr
2EI
0.5l 2
（9－4）
第9章 压杆稳定
图9－8
第9章 压杆稳定
3.一端固定一端铰支的细长压杆的临界载荷 图9－9所示为一端固定一端铰支的长为l的细长压杆， 在微弯临界状态，其拐点与铰支端之间的正弦半波曲线长为

材料力学-第9章压杆的稳定问题

材料力学-第9章压杆的稳定问题

0 1 0 sinkl coskl
sinkl 0
第9章 压杆的稳定问题
两端铰支压杆的临界载荷欧拉公式
sinkl 0
FP k EI 由此得到临界载荷
2
kl nπ, n 1, 2 ,,
FPcr
π 2 n 2 EI l2
最小临界载荷
FPcr π 2 EI 2 l
第9章 压杆的稳定问题
FPcr
π 2 EI
l
2
这一表达式称为欧拉公式。其中l为不同压杆屈曲后挠曲线上 正弦半波的长度，称为有效长度(effective length)； 为反映不同 支承影响的系数，称为长度系数（coefficient of 1ength），可由屈 曲后的正弦半波长度与两端铰支压杆初始屈曲时的正弦半波长度 的比值确定。
d2w M ( x) - EI 2 dx
d2w 2 k w0 2 dx
k2 FP EI
第9章 压杆的稳定问题
两端铰支压杆的临界载荷欧拉公式
d2w 2 k w0 2 dx
k2
FP EI
微分方程的解
w =Asinkx + Bcoskx
边界条件
w ( 0 ) = 0 , w( l ) = 0
第9章 压杆的稳定问题
临界应力与临界应力总图
对于某一压杆，当分叉载荷 FP 尚未算出时，不 能判断压杆横截面上的应力是否处于弹性范围；当 分叉载荷算出后，如果压杆横截面上的应力超过弹 性范围，则还需采用超过比例极限的分叉载荷计算 公式。这些都会给计算带来不便。 能否在计算分叉载荷之前，预先判断哪一类压 杆将发生弹性屈曲？哪一类压杆将发生超过比例极 限的非弹性屈曲？哪一类不发生屈曲而只有强度问 题？回答当然是肯定的。为了说明这一问题，需要 引进长细比（slenderness）的概念。

材料力学之压杆稳定

材料力学之压杆稳定

材料力学之压杆稳定引言材料力学是研究物体内部受力和变形的学科，压杆稳定是其中的一个重要内容。

压杆稳定是指在受到压力作用时，压杆能够保持稳定，不发生失稳或破坏的现象。

本文将介绍压杆稳定的基本原理、稳定条件以及一些常见的失稳形式。

压杆的受力分析在进行压杆稳定分析前，我们首先需要对压杆受力进行分析。

压杆通常是一根长条形材料，两端固定或铰接。

在受到外部压力作用时，压杆会受到内部的压力，这些压力会导致杆件产生变形和应力。

在分析压杆稳定性时，我们主要关注压杆的弯曲和侧向稳定性。

压杆的基本原理压杆的稳定性是由杆件的弯曲和侧向刚度共同决定的。

当压杆弯曲和侧向刚度足够大时，压杆能够保持稳定。

所以，为了提高压杆的稳定性，我们可以采取以下几种措施：1.增加杆件的截面面积，增加抗弯能力；2.增加杆件的高度或长度，增加抗弯刚度；3.增加杆件的横向剛性，增加抗侧向位移能力；4.添加支撑或加固结构，增加整体稳定性。

压杆的稳定条件压杆稳定的基本条件是在承受外部压力时，内部应力不超过材料的极限强度。

当内部应力超过材料的极限强度时，压杆将会发生失稳或破坏。

在实际工程中，我们一般采用压杆的临界压力比来判断压杆的稳定性。

临界压力比是指杆件在失稳前的临界弯曲载荷与临界弯曲载荷之比。

当临界压力比大于1时，压杆是稳定的；当临界压力比小于1时，压杆是不稳定的。

临界压力比的计算可以采用欧拉公式或者Vlasov公式等方法。

这些方法能够给出压杆在不同边界条件下的临界压力比。

在工程实践中，我们可以根据具体问题选择合适的方法来计算临界压力比。

压杆的失稳形式压杆失稳通常有两种形式：弯曲失稳和侧向失稳。

弯曲失稳压杆的弯曲失稳是指杆件在受到外部压力作用时，发生弯曲变形并导致失稳。

在弯曲失稳中，压杆的弯曲形态可以分为四种：1.局部弯曲失稳：杆件出现弯曲局部失稳，形成凸起或凹陷；2.局部弯扭失稳：杆件出现弯曲和扭曲共同失稳；3.全截面失稳：整个杆件截面均发生失稳；4.全体失稳：整个杆件完全失稳并失去稳定性。

材料力学_压杆稳定

材料力学_压杆稳定

π 2E λp = σp
欧拉公式仅适用于细长压杆的稳定计算
对Q235 钢,E=200GPa,σp=200MPa,则 , ,
200 × 109 λp = π ≈ 100 6 200 × 10
9.2 压杆的临界应力
二,临界应力总图 大柔度压杆(细长压杆 : 大柔度压杆 细长压杆): 细长压杆
σ cr σs
π 2 EI π 2E Fcr σ cr = = = 2 A (l / i )2 A(l )
其中
记
λ=
l
i
压杆的柔度或 压杆的柔度或长细比 欧拉临界应力
i=
I A
π 2E σ cr = 2 λ
(λ = λmax )
π 2E π 2E σ cr = 2 ≤ σ p λ ≥ λ σp
大柔度压杆(细长压杆 : 大柔度压杆 细长压杆): λ ≥ λ p 细长压杆
σp
σ cr = σ s
σcr = a1 b1λ
2
π 2E σ cr = 2 λ
直线经验公式: 直线经验公式:
(λ ≥ λ p )
σ cr = a bλ
σ cr = π E λ2
2
中柔度压杆(中长压杆 中柔度压杆 中长压杆) 中长压杆
σ cr = a bλ (λs ≤ λ ≤ λ p )
σ cr ≤ σ s (σ b ) λs =
2
d y = M ( x) = M B + FBy (l x) Fy 2 dx
2
k2 =
F EI ~ M M= B F
y
A
y (0) = 0 y′(0) = 0 y (l ) = 0 y′(l ) = 0 ~ ~ B + M + F l = 0 0 1 1 l ~ k 0 0 1 A k F = 0 =0 ~ sin kl cos kl 1 0 A sin kl + B cos kl + M = 0 ~ k cos kl k sin kl 0 1 kA cos kl kB sin kl F = 0 kl sin = 0 or Det = k[kl sin kl 2(1 cos kl )] 2 kl kl kl kl kl = 2k sin ( kl cos 2 sin ) = 0 (kl cos 2 sin ) = 0 2 2 2 2 2

材料力学答案- 压杆稳定

材料力学答案- 压杆稳定

15-1 两端为球铰的压杆，当它的横截面为图示各种不同形状时，试问杆件会在哪个平面内失去稳定（即在失稳时，杆的截面绕哪一根轴转动）？解：(a),(b),(e)任意方向转动，(c),(d),(f)绕图示Z 轴转动。

15-2 图示各圆截面压杆，横截面积及材料都相同，直径d ＝1.6cm ，杆材A 3钢的弹性模量E =200MPa ，各杆长度及支承形式如图示，试求其中最大的与最小的临界力之值。

解：(a) 柔度： 2301500.4λ⨯== 相当长度：20.30.6l m μ=⨯=(b) 柔度： 1501250.4λ⨯== 相当长度：10.50.5l m μ=⨯=(c) 柔度： 0.770122.50.4λ⨯== 相当长度：0.70.70.49l m μ=⨯=(d) 柔度： 0.590112.50.4λ⨯== 相当长度：0.50.90.45l m μ=⨯=(e) 柔度： 145112.50.4λ⨯== 相当长度：10.450.45l m μ=⨯=由E=200Gpa 及各柔度值看出：各压杆的临界力可用欧拉公式计算。

即：()22cr EIF l πμ=各压杆的EJ 均相同，故相当长度最大的压杆(a)临界力最小，压杆(d)与(e)的临界力最大，分别为：()2948222320010 1.610640.617.6410cr EFF l N πππμ-⨯⨯⨯⨯⨯===⨯()2948222320010 1.610640.4531.3010cr EIF l Nπππμ-⨯⨯⨯⨯⨯===⨯15-3 某种钢材P σ=230MPa ，s σ=274MPa ，E =200GPa ，直线公式λσ22.1338-=cr ，试计算该材料压杆的P λ及S λ值，并绘制1500≤≤λ范围内的临界应力总图。

解：92.633827452.5p s s a λπσλ===--===15-4 6120型柴油机挺杆为45钢制成的空心圆截面杆，其外径和内径分别为，12mm 和10mm ，杆长为383mm ，两端为铰支座，材料的E ＝210GPa ，P σ=288MPa ，试求此挺杆的临界力cr F 。

材料力学第九章 压杆稳定


02
创新研究方法与手段
积极探索新的实验技术和数值模拟方法，提高压杆稳定研究的精度和可
靠性。
03
拓展应用领域
将压杆稳定研究成果应用于更多领域，解决实际工程问题，推动科学技
术进步。
THANKS
感谢观看
稳定性取决于压杆的初始弯曲程度、压力的大小 和杆件的材料特性。
当压杆受到微小扰动时，如果能够恢复到原来的 平衡状态，则称其为稳定；反之，则为不稳定。
压杆的临界载荷
临界载荷是指使压杆由稳定平衡 状态转变为不稳定平衡状态的载
荷。
当压杆所受压力小于临界载荷时， 压杆保持稳定平衡状态；当压力 大于临界载荷时，压杆将失去稳
相应措施进行解决。
建筑结构中的压杆问题
02
高层建筑、大跨度结构等建筑中的梁、柱等部件可能发生失稳，
需要加强设计和施工控制。
压力容器中的压杆问题
03
压力容器中的管道、支撑部件等可能发生失稳，需要采取相应
的预防和应对措施。
05
压杆稳定的未来发展与展望
压杆稳定研究的新趋势
跨学科交叉研究
压杆稳定与材料科学、计算科学、工程结构等领域相互渗透，形 成多学科交叉的研究趋势。
工程中常见的压杆问题
1 2
细长杆失稳
细长杆在压力作用下容易发生弯曲，导致失稳。
短粗杆失稳
短粗杆在压力作用下可能发生局部屈曲，导致失 稳。
3
弹性失稳
材料在压力作用下发生弹性变形，当压力超过某 一临界值时，杆件发生失稳。
解决压杆失稳的方法与措施
加强材料质量
选择优质材料，提高材料的弹 性模量和抗拉强度，以增强压
材料力学第九章 压杆稳 定
• 引言 • 压杆稳定的基本理论 • 压杆稳定的实验研究 • 压杆稳定的工程应用 • 压杆稳定的未来发展与展望

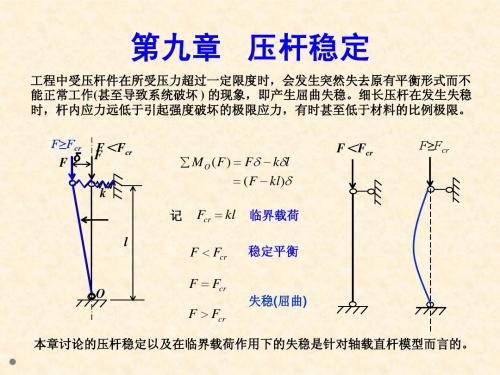
材料力学-压杆稳定


1．直线型经验公式
对于柔度(λs≤λ<λp)的中柔 度杆（中长压杆），临界应力 与λ的关系采用直线公式：
cr a b 13 8
式(13-8)中的系数a,b可查书中表 13-1。 λ的最低界限：
s
a
s
b
(塑性材料)
b
a
b
b
(脆性材料)
---------(13-9)
图13-3
2．抛物线型经验公式
式中有c1,c2,k三个未知量。根据边界条件：当x=0时， yA=0；代入式(c)得c2=0。式(c)成为
y c1 sinkx (d )
当x=l时，yB=0；代入式(d)后可得 c1 sinkl 0 (e)
要满足式(e)，必然是c1或sinkl等于零，若c1=0，则压杆 上各点的位移都为零，这显然与压杆在微弯状态下保持平衡 的前提不符，故必须是sinkl=0。要满足这一条件的kl值为：
kl 0, ,2 ,L ,n （n为正整数）
由k P n 可得：
EI l
P
n2 2 EI
l2
(
f
)
使压杆可能在微弯状态下保持平衡的最大轴向压力，应
该是式(f) 中n=1时的P值，这就是所求的两端铰支压杆的临
界力Pcr，即
Pcr
2 EI
l2
(13 1)
式(13-1)习惯上称为两端铰支压杆的欧拉公式。当各个 方向的支承情况相同时（如两端为球铰），压杆总是在它的 抗弯能力最小的纵向平面内失稳，所以式(13-1)中的EI是压 杆的最小抗弯刚度，即I应取截面的最小形心主惯性矩Imin。
2
图13-4 对于柔度(λ<λc)的杆件，临界应力与λ的关系采用抛物线公式：

材料力学-压杆的稳定性

例题：两端铰支压杆的长度 l = 1.2m，材料为 Q235 钢，其弹性摸 量 E=200GPa，1=200MPa，2=235MPa。已知截面的面积 A=900mm2，若截面的形状分别为正方形和 d/D = 0.7的空心圆管， 试计算各杆的临界力。
11.5 压杆的稳定计算
一、安全系数法
Fcr F [F ] nst
I A
•临界柔度
s — 屈服极限
2E 1 欧拉公式 (大柔度杆) cr 2 1 2 (中柔度杆) cr a b 直线公式
•临界应力
2
(小柔度杆)
cr s
强度问题
临界应力总图：临界应力与柔度之间的变化关系图。
cr
S P
许可外力 [ P ] 。
a
A
30
0
b
P B
C
D
例题：
11.6 提高压杆稳定性的措施
FPcr
2 EI ( l )2
欧拉公式
FPcr 越大越稳定
1) 减小压杆长度 l 2) 减小长度系数μ（增强约束）
3) 增大截面惯性矩 I（合理选择截面形状）
4) 增大弹性模量 E（合理选择材料）
1) 减小压杆长度 l
（绕哪个轴转动）
对于矩形截面：
y
压杆的稳定性
y
h b z
x h z b
1 3 I z bh , 12
1 3 I y hb 12
hb
Iz Iy
所以该矩形截面压杆应在xz平面内 失稳弯曲；即，绕 y 轴转动。
11.3 其他支座条件下细长压杆的临界压力
对于其他支座条件下细长压杆，求临界压力有两种方法：

材料力学-压杆稳定


P
P
P
a 1.3 a
1.6a
(1)
(2)
(3)
相当长度 (l)1 2a (l)2 1.3a
(l)3 0.7 1.6a 1.12a
l1 l2 l3
Fcr

2EI
l 2
a 1.3 a
1.6a
F
F
F
(1)
(2)
(3)
Fcr1 Fcr2 Fcr3
L
C
Fcr

2 EI
(0.5l )2
长度系数
一端固定、一端自由 两端铰支
一端固定、一端铰支
Fcr

(
2 EI
2.0 l )2
2 EI
Fcr ( 1.0 l )2
Fcr

(
2 EI
0.7 l )2
两端固定
Fcr

2 EI ( l )2
Fcr

2 EI
( 0.5 l )2
欧拉公式普遍形式
长度系数
l 相当长度
2
1
0.7
0.5
杆端的约束愈强，则µ值愈小，压杆的临界力愈高； 杆端的约束愈弱，则值µ愈大，压杆的临界力愈低。
l
l i
Fcr cr A
例1 ： 图示各杆材料和截面均相同，试问哪一 根杆能承受的压力最大， 哪一根的最小？
118 26.6 4.42 nst 3
5、结论
AB杆满足稳定性要求
1、圆截面杆BD的直径为ｄ＝35毫米，采用普通碳 钢，弹性模量 Ｅ＝200GPａ，比例极限为σP＝ 200MPａ，屈服极限为σS＝235MPａ，ａ＝304 MPａ，ｂ＝1.12 MPａ，稳定安全系数取ｎw＝3， 载荷G＝30K N，校核BD杆的稳定性。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

压杆稳定
22-1如图所示三根杆，EI 相同，若杆2为细长杆，其临界载荷为cr F ，则杆1的临界载荷（ a ）4
cr
F ，杆3的临界载荷（ c ）4cr F 。

（a ）一定等于； （b ）一定不等于； （c ）不一定等于。

22-2若两端约束条件相同的压杆，其截面如图所示。

试问当压杆失稳时，它的横截面绕哪一根轴转动(y ,z 轴为形心轴)？
(a) (b) (c)
(d) (e) (f)
解：(a)、(b)、(d)可绕通过形心的任意轴转动，(c)、(e)、(f)绕y 轴转动。

22-3矩形截面压杆，边长分别为12b mm =，20h mm =，杆长300l mm =，材料为Q235钢，206E GPa =，试计算下列三种情况下的临界载荷（若为中长压杆，选用直线公式）。

（1）一端固定，一端自由；
（2）两端铰支； （3）两端固定。

解：min
i ==
（1）一端固定，一端自由： 2μ=
min
173.2100p l
l
i b
μλλ=
=
=>≈，此杆为细长杆，算用欧拉公式 22
16.3cr cr Ebh
F A kN πσλ=== （2）两端铰支：1μ=
min
86.6100p l
l
i b
μλλ=
=
=<≈ 060λλ>≈，此杆为中长压杆，采用直线公式，
()49.7cr cr F A bh a b kN σλ==-= （3）两端固定：0.5μ=
min
43.3s l
l
i b
μλλ=
=
=<，此杆为短粗杆，56.4cr s F bh kN σ== 22-4如图所示的细长压杆均为圆杆，其直径d 均相同．材料是Q235钢，210E GPa =。

其中：图（a ）为两端铰；（b ）为一端固定，一端铰支；图(c)为两端固定。

试判别哪一种情形的临界力最大，哪种其次，哪种最小?若圆杆直径
160d mm =，试求最大的临界力cr F 。

解：压杆横截面的惯性矩 4
4
540.16 3.2171064
64
d I m ππ-⨯=
=
=⨯
100
p
λπ
===
压杆横截面的惯性半径
0.04
4
d
i m
===
图（a）1
μ=5
l m
=
15
125
0.04p
l
i
μ
λλ
⨯
===>，所以杆件是细长杆。

2297
22
21010 3.21710
2667
()(15)
cr
EI
F kN
l
ππ
μ
-
⨯⨯⨯⨯
===
⨯
图（b）0.7
μ=7
l m
=
0.77
122.5
0.04p
l
i
μ
λλ
⨯
===>，所以杆件是细长杆。

2297
22
21010 3.21710
2777
()(0.77)
cr
EI
F kN
l
ππ
μ
-
⨯⨯⨯⨯
===
⨯
图（c）0.5
μ=9
l m
=
0.59
112.5
0.04p
l
i
μ
λλ
⨯
===>，所以杆件是细长杆。

2297
22
21010 3.21710
3293
()(0.59)
cr
EI
F kN
l
ππ
μ
-
⨯⨯⨯⨯
===
⨯
22-5如图所示托架中杆AB的直径40
d mm
=，80
l mm
=，两端可视为铰支，材料是Q235钢。

（1）试按杆AB的稳定条件求托架的临界力。

（2）若已知实际载荷70
F kN
=,稳定安全系数[]2
st
n=，问此托架是否安全？
解：（1）托架的临界力
0.63
cos
0.84
α==
取横杆CD为研究对象，作受力图，由平衡条件
C
M=
∑0.9s i n0.6
B
F Fα
-⨯=
可得杆AB 的轴力 0.9 2.2680.6sin B F
F F a
=
=
杆AB 两端铰支，1μ=。

材料Q235钢，100p λ=，060λ=，
0.014
d
i m =
== 10.8800.01l i μλ⨯=== 0p λλλ>>，不能用欧拉公式计算临界力，应用经验公式计算临界力。

查表310a MPa =， 1.14b MPa =，杆AB 的临界力，
2
26
0.04(310 1.1480)10()2754
4
Bcr cr d F A a b kN ππσλ⨯-⨯⨯==
-=
=
托架的临界力， 2.268Bcr F F =，所以275
121.32.268 2.268
B F F kN === （2）校核托架的稳定安全性
2.268B F F =
Bcr st B
F
n F = []275 1.7322.26870
cr st st B F n n F =
==<⨯ ，所以不安全。

22-6图示结构中，梁AB 采用No.14工字钢，柱CD 为圆截面直杆，其直径20d mm =，二者材料均为Q235钢。

结构受力如图所示，若已知25F kN =，
1 1.25l m =，20.55l m =，强度安全因数 1.45n =，稳定安全因数[] 1.8st n =，试校核此结构是否安全。

（3310210z W mm =⨯，2221.510A mm =⨯）
解：梁AB 处于拉弯组合变形状态，需进行强度校核，柱CD 受压，需进行稳定校核。

1.梁AB 的强度校核。

梁AB 的中点C 为危险截面，此处弯矩和轴力分别为,
1sin3015.63M F l kN m =⨯= cos3021.65N F F kN ==
max 163.2N
z F M MPa W A
σ=
+= []2351621.45s MPa n σσ==
=
163.2162
100%0.7%5%162
-⨯=< 所以工程上认为梁AB 是安全。

2.压杆CD 的稳定性校核
工作压力 2sin3025CD F F kN ==
54d i mm == 310.55101101005
p l i μλλ⨯⨯===>≈ 22
52.8()
cr EI
F kN l πμ== []2.1cr st st CD F n n F ==> 所以杆CD 稳定。