电路定理的相量形式1
- 格式:ppt
- 大小:897.00 KB
- 文档页数:18









课程编码:07153102
电路原理课程教案2007 ~2008 学年第一学期
任课教师:申铉京
吉林大学计算机科学与技术学院
课程名称:电路
课程英文名称: Electric Circuit Theory
学时: 48
学分: 3
授课对象:计算机科学与技术专业 07 级1--12班
教学目的:
电路原理课程(Electric Circuit Theory), 适应于计算机科学技术专业本科生的学科基础必修课。
电路课程是电气类专业的一门重要技术基础课, 通过本课程的学习, 使学生掌握电路的基本理论、电路的分析计算方法和进行实验的初步能力, 并为后续课程的学习准备必要的基本知识。
电路课程理论严密, 实践性强, 对于训练学生的辩证思维能方式和树立理论联系实际的观点与提高分析问题与解决问题的能力, 都具有重要作用。
教学方式:理论授课,多媒体,板书
教材:《电路》,邱关源编,高等教育出版社出版(第四版)
教学参考书:
1>电路分析简明教程,付恩锡主编,高等教育出版社,2004年1
月出版;
2>电路原理,周守昌主编,高等教育出版社,2004年8月(第二
版)。
第8章相量法8.1 复习笔记一、复数相关知识点1.复数的表示形式如图8-1-1所示,在复平面内有一个向量F,可以用以下几种方式表示:(1)代数形式(2)三角函数形式F=|F|(cosθ+jsinθ)(3)指数形式F=|F|e jθe jθ=cosθ+jsinθ(欧拉公式)(4)极坐标形式F=|F|∠θ图8-1-12.复数运算设有两个复数分别为F1=a1+jb1,F2=a2+jb2。
(1)加减运算F1±F2=(a1+jb1)±(a2+jb2)=(a1±a2)+j(b1±b2)复数的加减运算在复平面上符合平行四边形求和法则,如图8-1-2所示。
图8-1-2 复数的加减运算(2)乘法运算所以|F1F2|=|F1||F2|arg(F1F2)=arg(F1)+arg(F2)(3)除法运算所以(4)旋转因子①e jθ=1∠θ,若则②e jπ/2=j,e-jπ/2=-j,e jπ=-1,e j2π=1。
二、相量法基础(1)正弦量的表达式:u(t)=U m cos(ωt+φ)。
式中,U m为振幅,ω为角频率,φ为初相,三者称为正弦量的三要素。
有效值即其均方根值相量:表征正弦时间函数的复值常数。
(2)有效值相量:U▪=U∠φu,复值常数的模表示有效值,由此可知(3)正弦量的相量表示法:分为有效值相量和最大值相量。
例如,正弦量其有效值相量I▪=10∠50°A。
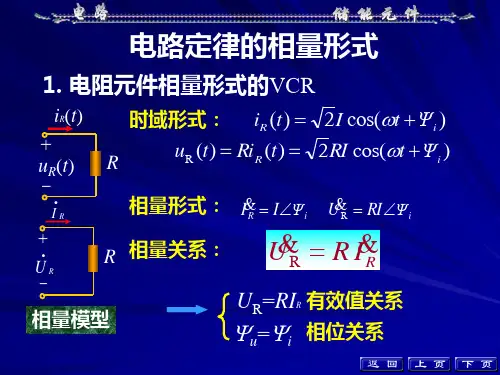
其对应的最大值相量三、电路定律的相量形式(1)KCL、KVL定律的相量形式∑I▪=0∑U▪=0(2)电路元件VCR的相量形式①电阻元件:U▪=R I▪。
即电阻上的电压和电流同相位,相量图如图8-1-3所示。
图8-1-3②电感元件:U▪=jωL I▪。
即电感上的电压超前电流90°,相量图如图8-1-4所示。
图8-1-4③电容元件:U▪=I▪/(jωC)即电容上的电压滞后电流90°,相量图如图8-1-5所示。
第二章正弦交流电路2.1.1 正弦量的三要素及表示方法(1)正弦交流电路:如果在线性电路中施加正弦激励(正弦交流电压源或正弦交流电流源),则电路中的所有响应在电路达到稳态时,也都是与激励同频率的正弦量,这样的电路称为正弦交流电路。
(2)正弦交流电压或正弦交流电流等物理量统称为正弦量,它们的特征表现在变化的快慢、大小及初值3个方面,分别由频率(或周期)、幅值(或有效值)和初相位来确定。
所以称频率、幅值(或有效值)和初相位为正弦量的三要素。
(3)因为正弦量具有3个要素,它们完全可以表达对应的正弦量的特点和共性。
所以,只要能够反映出正弦的三要素,就可以找到多种表示正弦量的方法,其常见的表示方法如下。
①三角函数表示法和正弦波形图示法,比如正弦电压u=U m sin(ωt+φ),其正弦波形如图2.1所示,但是正弦量的这两种表示方法都不利于计算。
②旋转矢量表示法,由于复平面上一个逆时针方向旋转的复数能够反映出正弦量的3个要素,因此可用来表示正弦量。
③相量及相量图表示法,由于正弦交流电路中的激励和响应均为同频率的正弦量,故可在已知频率的情况下,只研究幅值和初相位的问题。
这样,不仅可以用旋转矢量表示正弦量,而且也能把正弦量表示成复数(该复数与一个正弦量对应,称为相量)。
图2.1所示正弦电压的幅值相量和有效值相量分别为2.1.2 电路基本定律的相量形式将正弦量用相量表示有利于简化电路的分析和计算,其中电路分析的基本定律在频域中也是成立的,即为表2.1的电路基本定律的相量形式。
当用相量来表示正弦电压与电流,用复阻抗来表示电阻、电感和电容时,正弦交流电路的分析与计算也就类似于直流电路,复阻抗的串并联等效、支路电流法、叠加定理和戴维宁定理等分析方法均可应用。
为了研究复杂正弦交流电路中激励与响应之间的关系,以及研究电路中能量的转换与功率问题,就必须首先掌握单一参数(电阻、电感、电容)元件在正弦交流电路中的特性(见表2.2),以作为分析复杂正弦交流电路的基础。
第一章:电路模型和电路定理 一.电流、电压、功率概念1.电流的参考方向可以任意指定,分析时:假设参考方向与实际方向一致,则i>0,反之i<0。
电压的参考方向也可以任意指定,分析时:假设参考方向与实际方向一致,则u>0反之u<0。
2. 功率平衡一个实际的电路中,电源发出的功率总是等于负载消耗的功率。
3.欧姆定律:,,运用欧姆定理的时候要先判断电压与电流方向是否关联,如果不关联需要加负号 4. 电路的断路与短路电路的断路处:I =0,U≠0 电路的短路处:U =0,I≠0 三. 基尔霍夫定律 1. 几个概念:支路:是电路的一个分支。
结点:三条〔或三条以上〕支路的联接点称为结点。
回路:由支路构成的闭合路径称为回路。
网孔:电路中无其他支路穿过的回路称为网孔。
2. 基尔霍夫电流定律:〔1〕 定义:任一时刻,流入一个结点的电流的代数和为零。
或者说:流入的电流等于流出的电流。
〔2〕 表达式:i 进总和=0 或: i 进=i 出 〔3〕 可以推广到一个闭合面。
3. 基尔霍夫电压定律〔1〕 定义:经过任何一个闭合的路径,电压的升等于电压的降。
或者说:在一个闭合的回路中,电压的代数和为零。
或者说:在一个闭合的回路中,电阻上的电压降之和等于电源的电动势之和。
〔2〕基尔霍夫电压定律可以推广到一个非闭合回路 第二章电阻电路的等效变换概念:两个两端电路,端口具有相同的电压、电流关系,则称它们是等效的电路。
对外等效,对内不等效2. 串联电路的总电阻等于各分电阻之和,各电阻顺序连接,流过同一电流,串联电阻具有分压作用,Ri u =i u R =Gu R u i ==u R R R u 2111+=u R R R u 2122+=3.电阻并联等效电导等于并联的各电导之和,并联电阻具有分流作用4. 电阻的Y 形连接和形连接的等效变换,。
假设三个电阻相等(对称),则有5. 理想电压源〔1〕 不管负载电阻的大小,不管输出电流的大小,理想电压源的输出电压不变。
rlc串联电路相量表达式
RLC串联电路是由电阻(R)、电感(L)和电容(C)依次串联而成的电路,其相量表达式可以通过计算电压和电流的相位差来得到。
设电压的相量表示为V,电流的相量表示为I,频率为ω,电阻值为R,电感值为L,电容值为C。
电压和电流之间的相位差可以通过以下方式计算:
1.首先,计算电阻R对电压和电流的相位角影响,这两者之
间的相位差为0。
2.计算电感L对电压和电流的相位角影响。
电感引起的相位
差为θL = arctan(ωL)。
3.计算电容C对电压和电流的相位角影响。
电容引起的相位
差为θC = -arctan(1/(ωC))。
综上所述,RLC串联电路的相量表达式为:
V = I * (R + jωL - 1/(jωC))
其中,j是虚数单位。
该表达式可以用于计算电压和电流之间的相量关系,在研究和分析RLC串联电路的特性和行为时很有用。