大学物理下综合练习题

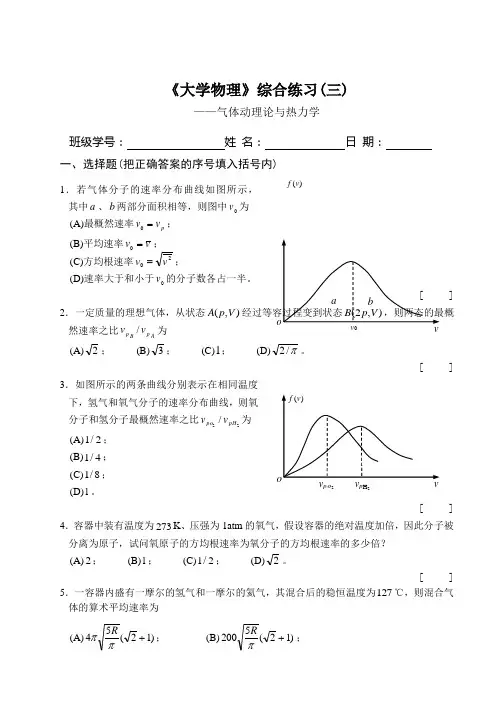
《大学物理》综合练习(三)——气体动理论与热力学班级学号： 姓 名： 日 期： 一、选择题(把正确答案的序号填入括号内)1．若气体分子的速率分布曲线如图所示， 其中a 、b 两部分面积相等，则图中0v 为 (A)最概然速率p v v =0； (B)平均速率v v =0； (C)方均根速率20v v =；(D)速率大于和小于0v 的分子数各占一半。

2．一定质量的理想气体，从状态),(V p A 然速率之比Ap Bp v v /为(A)2； (B)3； (C)1； (D)π/2。

[ ]3．如图所示的两条曲线分别表示在相同温度下，氢气和氧气分子的速率分布曲线，则氧分子和氢分子最概然速率之比22/pH po v v 为 (A)2/1； (B)4/1； (C)8/1； (D)1。

[ ]4．容器中装有温度为273K 、压强为1atm 的氧气，假设容器的绝对温度加倍，因此分子被分离为原子，试问氧原子的方均根速率为氧分子的方均根速率的多少倍？ (A)2； (B)1； (C)2/1； (D)2。

[ ]5．一容器内盛有一摩尔的氢气和一摩尔的氦气，其混合后的稳恒温度为127℃，则混合气体的算术平均速率为 (A))12(54+ππR； (B))12(5200+πR；f (v )p o 2 p H 22(C)πR15200； (D) π310400R。

[ ]6．气体的温度升高时，麦克斯韦速率分布函数曲线的变化是 (A)曲线下的面积增大，最概然速率增大； (B)曲线下的面积不变，最概然速率增大； (C)曲线下的面积减小，最概然速率增大； (D)曲线下的面积不变，最概然速率减小。

[ ]7．一容器装着一定量的某种气体，下述几种说法哪一种对? (A) 容器内各部分压强相等，这状态一定是平衡态； (B) 容器内各部分温度相等，这状态一定是平衡态；(C) 容器内各部分压强相等，且各部分密度也相同，这状态一定是平衡态。

[ ]8．图中表示在不同条件下理想气体的体积密度ρ随压强变化的五种曲线，试问哪个图准确地描述了等温条件下一定质量的气体的密度随压强的变化?[ ]9．理想气体作一循环过程acba ，其中ba 为等压过程，acb 为半圆弧， a c p p 2=。

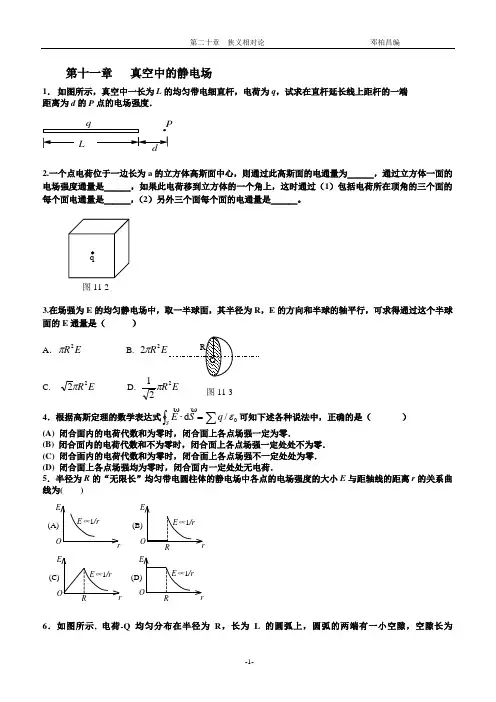
第十一章真空中的静电场1．如图所示，真空中一长为L的均匀带电细直杆，电荷为q，试求在直杆延长线上距杆的一端距离为d的P点的电场强度．LP2.一个点电荷位于一边长为a的立方体高斯面中心，则通过此高斯面的电通量为ˍˍˍ，通过立方体一面的电场强度通量是ˍˍˍ，如果此电荷移到立方体的一个角上，这时通过（1）包括电荷所在顶角的三个面的每个面电通量是ˍˍˍ，（2）另外三个面每个面的电通量是ˍˍˍ。

3.在场强为E的均匀静电场中，取一半球面，其半径为R，E的方向和半球的轴平行，可求得通过这个半球面的E通量是（）A．ER2π B.R22πC. ER22π D. ER221π4．根据高斯定理的数学表达式⎰∑⋅=SqSE/dεϖϖ可知下述各种说法中，正确的是（）(A) 闭合面内的电荷代数和为零时，闭合面上各点场强一定为零．(B) 闭合面内的电荷代数和不为零时，闭合面上各点场强一定处处不为零．(C) 闭合面内的电荷代数和为零时，闭合面上各点场强不一定处处为零．(D) 闭合面上各点场强均为零时，闭合面内一定处处无电荷．5．半径为R的“无限长”均匀带电圆柱体的静电场中各点的电场强度的大小E与距轴线的距离r的关系曲线为( )EOr(A)E∝1/r6．如图所示, 电荷-Q均匀分布在半径为R，长为L的圆弧上，圆弧的两端有一小空隙，空隙长为图11-2图11-3)(R L L <<∆∆，则圆弧中心O 点的电场强度和电势分别为( ) Ａ．R Q i L R L Q 0204,4πεπε-∆-ρ Ｂ．RQ i L R L Q 02024,8πεεπ-∆-ρ Ｃ．RQ i L R L Q 0204,4πεπερ∆ Ｄ．RL L Q i L R L Q 0204,4πεπε∆-∆-ρ7.如图所示,两同心带电球面，内球面半径为r 1＝5 cm ，带电荷q 1＝3×10-8 C ；外球面半径为r 2＝20 cm ， 带电荷q 2＝－6×10­8C ，设无穷远处电势为零，则空间另一电势为零的球面半径r ＝ __________________a 的“无限长”圆柱面上均匀带电，其电荷线密度为λ．在它外面同轴地套一半径为b 的薄金属圆筒，圆筒原先不带电，但与地连接．设地的电势为零，则在内圆柱面里面、距离轴线为r 的P点的场强大小和电势分别为（ ） (A) E ＝0，U ＝r a ln 20ελπ． (C) E ＝r 02ελπ，U ＝rb ln 20ελπ (B) E ＝0，U ＝a b ln 20ελπ (D) E ＝r 02ελπ，U ＝a b ln 20ελπ．9．如图，在点电荷+Q ，-Q 产生的电场中，abcd 为同一直线上等间距的四个点，若将一点电荷+q 0由b 点移到d 点，则电场力（ ）A. 作正功；B. 作负功；C.不作功;D.不能确定图11-6 a b c d +Q-Q 图11-910．说明下列各式的物理意义（1）l d E ρρ⋅（2）l d E b a ρρ⋅⎰（3）l d E L ρρ⋅⎰（4）S d E ρρ⋅11．已知某静电场的电势函数)(14121222SI y y x x U --=，由场强和电势梯度的关系式可得点（2，3，0）处的场强E ρ=ˍˍˍi ρ+ˍˍˍj ρ+ˍˍˍk ρ(SI)答案:1.()d L d q +π04ε 2. 00024,0,6,εεεq q q 3.A4.C5.C6. A7. 10cm8.B9.A10. （1）l d E ρρ⋅表示电场力对单位正电荷所做的元功。

大学物理（下）练习题第十章10－8一均匀带电的半圆形弧线，半径为R ，所带电量为Q ，以匀角速度ω绕轴OO /转动，如图所示，求O 点处的磁感应强度。

解：此题可利用运动电荷产生的磁场计算，也可利用圆电流产生的磁场计算。

以下根据圆电流在轴线产生的磁感应强度来计算的。

如图电荷dq 旋转在O 处产生的磁感应强度为3202R dIr dB μ=3202)sin (2RR Rd θπωθλμ= ⎰πθθπλωμ=020sin 4d B 240ππλωμ=80λωμ= RQπωμ=80 方向沿轴线向上。

10－15一半径为R 的无限长半圆柱面形导体，与轴线上的长直导线载有等值反向的电流I ，如图所示。

试求轴线上长直导线单位长度所受的磁力。

解：此电流结构俯视如图，圆柱面上的电流 与轴线电流反向，反向电流电流相斥，如图，对 称分析可知，合力沿x 轴正向，有θππμ==Rd R IR I BldI dF 20θπμ=d RI 2202=θ=⎰sin dF F θθπμ⎰πd RI 0220sin 2 RI 220πμ=习题 10－8图习题 10－15图x10－16半径为R 的圆形线圈载有电流I 2，无限长载有电流I 1的直导线沿线圈直径方向放置，求圆形线圈所受到的磁力。

解：此电流结构如图，对称分析可知，合力沿x 轴负向，有r I dl I dF πμ=2102θθπμ=Rd R I I cos 2210θθπμ=d II cos 2210=θ=⎰cos dF F θθθπμ=⎰πd I I cos cos 220210⎰πθπμ=202102d II 210I μ=10－19一半径为R 的薄圆盘，放在磁感应强度为B的均匀磁场中，B 的方向与盘面平行，如图所示，圆盘表面的电荷面密度为σ，若圆盘以角速度ω绕其轴线转动，试求作用在圆盘上的磁力矩。

解：圆盘上任一薄层电荷运转时产生的电流为dI ，其对应的磁矩为rdr r rdrr dI dm σω=ππωπσ=π=2222 整个圆盘的磁矩为44R rdr dm m Rσωπ=σω==⎰⎰作用在圆盘上的磁力矩为B m M ⨯====mB mB M 090sin B R 44σωπ,方向垂直纸面向里。

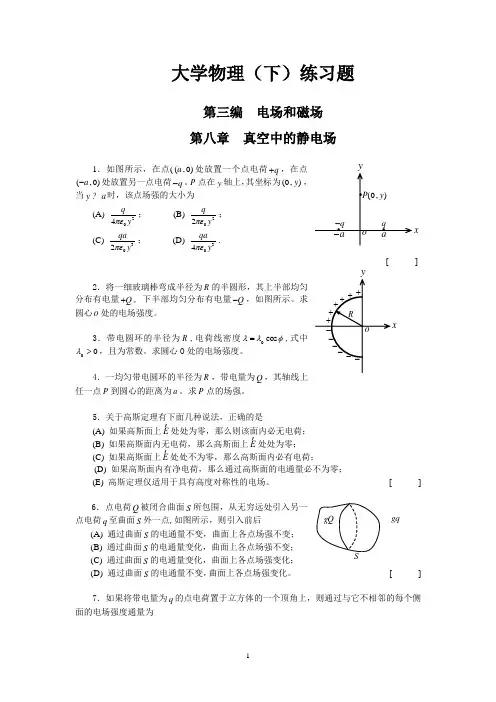
xyoa•••a-(0,)P y qq-大学物理（下）练习题第三编 电场和磁场 第八章 真空中的静电场1．如图所示，在点((,0)a 处放置一个点电荷q +，在点(,0)a -处放置另一点电荷q -。

P 点在y 轴上，其坐标为(0,)y ，当y a ?时，该点场强的大小为(A) 204q y πε； (B) 202q y πε；(C)302qa y πε； (D)304qa y πε.[ ]2．将一细玻璃棒弯成半径为R 的半圆形，其上半部均匀分布有电量Q +, 下半部均匀分布有电量Q -，如图所示。

求圆心o 处的电场强度。

3．带电圆环的半径为R ,电荷线密度0cos λλφ=,式中00λ>，且为常数。

求圆心O 处的电场强度。

4．一均匀带电圆环的半径为R ，带电量为Q ，其轴线上任一点P 到圆心的距离为a 。

求P 点的场强。

5．关于高斯定理有下面几种说法，正确的是(A) 如果高斯面上E r处处为零，那么则该面内必无电荷；(B) 如果高斯面内无电荷，那么高斯面上E r处处为零；(C) 如果高斯面上E r处处不为零，那么高斯面内必有电荷；(D) 如果高斯面内有净电荷，那么通过高斯面的电通量必不为零； (E) 高斯定理仅适用于具有高度对称性的电场。

[ ]6．点电荷Q 被闭合曲面S 所包围，从无穷远处引入另一点电荷q 至曲面S 外一点,如图所示，则引入前后(A) 通过曲面S 的电通量不变，曲面上各点场强不变；(B) 通过曲面S 的电通量变化，曲面上各点场强不变；(C) 通过曲面S 的电通量变化，曲面上各点场强变化；(D) 通过曲面S 的电通量不变，曲面上各点场强变化。

[ ]7．如果将带电量为q 的点电荷置于立方体的一个顶角上，则通过与它不相邻的每个侧面的电场强度通量为xq g S Q g(A)06q ε； (B) 012q ε； (C) 024q ε； (D) 048q ε. [ ]8．如图所示，A 、B 为真空中两个平行的“无限大”均匀带电平面，A 面上的电荷面密度721.7718A C m σ--=-⨯⋅，B 面上的电荷面密度723.5418B C m σ--=⨯⋅。

物理（下）作业专业班级：姓名：学号：第十章真空中的静电场(1)一、选择题1、根据电场强度定义式0/q F E（0q 为正的实验点电荷），下列说法中哪个是正确的？(A)、若场中某点不放实验电荷0q ，则F =0，从而E=0；(B)、电场中某点场强的大小与实验点电荷q 0的大小成反比；(C)、电场中某点场强的方向，就是正电荷在该点所受电场力的方向；(D)、以上说法都不正确。

[]2、如图所示，在坐标(a ，0)处放置一点电荷+q ，在坐标(-a ，0)处放置另一点电荷－q ．P点是x 轴上的一点，坐标为(x ，0)．当x >>a 时，该点场强的大小为：(A)xq04 ；(B)30xqa；(C)302xqa；(D)204xq 。

[]3、（2010年北京科技大学）两个带有等量同号电荷，形状相同的金属小球１和２，相互作用力为F ，它们之间的距离远大于小球本身直径．现在用一个带有绝缘柄的原来不带电的相同金属小球３去和小球１接触，再和小球２接触，然后移去．这样小球１和２之间的作用力变为：(A)F/2；(B)F/4；(C)3F/8；(D)F/10．[]二、填空题1、一电量为–5×10―9C 的试验电荷放在电场中某点时，受到20×10―9N 向下的力，则该点的电场强度大小为___________________，方向__________________。

2、（2011年电子科技大学）由一根绝缘细线围成的边长为l 的正方形线框，今使它均匀带电，其电荷线密度为λ，则在正方形中心处的电场强度大小Ｅ＝__________________。

3、铁原子核里两质子间相距4.0×10－15米，每个质子的电荷都是1.6×10－19库仑，则它们之间的库仑力应为______________牛顿。

三、计算题1、（2012年深圳大学）如图，在O x 轴上有长为a 的细杆OM ，其电荷线密度为Cx ，其中Ｃ为大于零的常量，求：(1)在OM 延长线上距Ｍ点为ｂ的Ｐ点的电场强度的大小；(2)如果在Ｐ点放置一个带电量为+q 的点电荷，该点电荷所受库仑力大小为多少？2、有一半径为R的半圆细环上均匀地分布电荷Q，若在其环心处放置一电荷量为q的点电荷，求该点电荷q所受到的电场力的大小及方向。