第六章李亚普诺夫稳定性分析
- 格式:ppt
- 大小:10.40 MB
- 文档页数:56

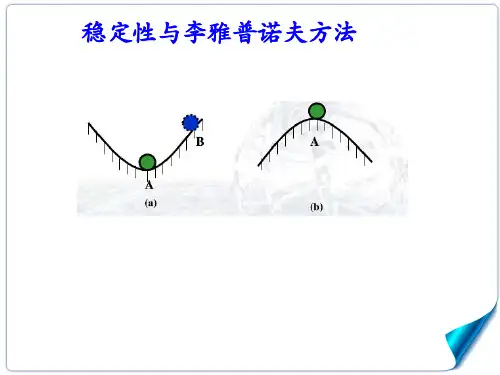
第六章稳定性与李雅普诺夫(Lyapunov)方法6.1 概述研究平衡状态及其稳定性介绍两类解决稳定性问题的方法,即Lyapunov 第一法和Lyapunov第二法。
第一法通过求解微分方程的解来分析运动稳定性,即通过分析非线性系统线性化方程特征值分布来判别原非线性系统的稳定性;第二法则是一种定性方法,它无需求解的非线性微分方程,通过构造一个Lyapunov函数,研究它的正定性及其对时间的沿系统方程解的全导数的负定或半负定,来得到稳定性的结论。
一般我们所说的Lyapunov方法就是指Lyapunov第二法。
虽然在非线性系统的稳定性分析中,Lyapunov 稳定性理论具有基础性的地位,但在具体确定许多非线性系统的稳定性时,需要技巧和经验。
6.2 Lyapunov 意义下的稳定性问题一、 平衡状态、给定运动与扰动方程之原点考虑如下非线性系统),(t x f x = (6.1)式中x 为n 维状态向量,),(t x f 是变量1x ,2x ,…,n x 和t 的n 维向量函数。
假设在给定初始条件下,式(6.1)有唯一解),;(00t x t Φ,且当0t t =时,0x x =。
于是0000),;(x t x t =Φ在式(6.1)的系统中,总存在0),(≡t x f e , 对所有t (6.2)则称e x 为系统的平衡状态或平衡点。
如果系统是线性定常的即 Ax t x f =),(当A 为非奇异矩阵时,系统存在一个唯一的平衡状态0=e x ;当A 为奇异矩阵时,系统将存在无穷多个平衡状态。
对于非线性系统,则有一个或多个平衡状态,这些状态对应于系统的常值解(对所有t ,总存在e x x =)。
任意一个孤立的平衡状态(即彼此孤立的平衡状态)或给定运动)(t x φ=都可通过坐标变换,统一化为扰动方程),~(~~t x f x = 之坐标原点,即0),0(~=t f 或0~=e x 。
在本章中,除非特别申明,我们将仅讨论扰动方程关于原点处之平衡状态的稳定性问题。








李雅普诺夫稳定性分析常微分⼤作业--李雅普诺夫稳定性11091059洪⼀洲从19世纪末以来,李雅普诺夫稳定性理论⼀直指导着关于稳定性的研究和应⽤。
不少学者遵循李雅普诺夫所开辟的研究路线对第⼆⽅法作了⼀些新的发展。
⼀⽅⾯,李雅普诺夫第⼆⽅法被推⼴到研究⼀般系统的稳定性。
例如,1957年,В.И.祖博夫将李雅普诺夫⽅法⽤于研究度量空间中不变集合的稳定性。
随后,J.P.拉萨尔等⼜对各种形式抽象系统的李雅普诺夫稳定性进⾏了研究。
在这些研究中,系统的描述不限于微分⽅程或差分⽅程,运动平衡状态已采⽤不变集合表⽰,李雅普诺夫函数是在更⼀般意义下定义的。
1967年,D.布肖对表征在集合与映射⽔平上的系统建⽴了李雅普诺夫第⼆⽅法。
这时,李雅普诺夫函数已不在实数域上取值,⽽是在有序定义的半格上取值。
另⼀⽅⾯,李雅普诺夫第⼆⽅法被⽤于研究⼤系统或多级系统的稳定性。
此时,李雅普诺夫函数被推⼴为向量形式,称为向量李雅普诺夫函数。
⽤这种⽅法可建⽴⼤系统稳定性的充分条件。
1.李雅普诺夫稳定性概念忽略输⼊后,⾮线性时变系统的状态⽅程如下),(t x f x= (1)式中,x 为n 维状态向量;t 为时间变量;),(t x f 为n 维函数,其展开式为 12(,,,,)i i n x f x x x t = n i ,,1 =假定⽅程的解为 ),;(00t x t x ,x 0和t 0 分别为初始状态向量和初始时刻,0000),;(x t x t x =。
平衡状态如果对于所有t ,满⾜0),(==t x f xe e (2)的状态x e 称为平衡状态(⼜称为平衡点)。
平衡状态的各分量不再随时间变化。
若已知状态⽅程,令0=x所求得的解x ,便是平衡状态。
对于线性定常系统Ax x= ,其平衡状态满⾜0=e Ax ,如果A ⾮奇异,系统只有惟⼀的零解,即存在⼀个位于状态空间原点的平衡状态。
⾄于⾮线性系统,0),(=t x f e 的解可能有多个,由系统状态⽅程决定。

§6.2李雅普诺夫稳定性1、稳定性定义李雅普诺夫稳定性概念如果对于任意给定的0>ε和0t ≥0都存在0),(0>=t εδδ,使得只要0x 满足δ<-10x x就有εϕ<-),,(),,(1000x x x t t t t对一切0t t ≥成立,则称微分方程),(d d x x t f t= (6.6)的解),,(10x x t t ϕ=是稳定的.否则是不稳定的.假设),,(10x x t t ϕ=是稳定的,而且存在)0(11δδδ≤<,使得只要0x 满足1δ<-10x x就有0)),,(),,((lim 1000=-∞→x x x t t t t t ϕ则称(6.6)的解),,(10x x t t ϕ=是渐近稳定的.注意:微分方程(6.6)式中的函数),(x t f 对nR D ⊆∈x 和(,)t ∈-∞+∞连续,对x 满足局部李普希兹条件.一般情况下,我们把解),,(10x x t t ϕ=的稳定性化成零解的稳定性问题进行讨论. 这样就有下面的关于零解0=x 稳定性的定义:定义1 若对任意0ε>和00t ≥,存在0),(0>=t εδδ,使当δ<0x 时有ε<),,(00x x t t对所有的0t t ≥成立,则称(6.6)的零解是稳定的.反之是不稳定的.定义2 若(6.6)的零解是稳定的,且存在10δ>, 使当1δ<0x 时有0),,(lim 00=∞→x x t t t则称(5.1)的零解是渐近稳定的. 2、李雅普诺夫第二方法定义3(李雅普诺夫函数) 若函数R G →:)(x V满足V (0)=0, )(x V 和),,2,1(n i x i=∂∂V 都连续,且若存在0<H ≤K ,使在{}H x x ≤=|D 上)0(0)(≤≥x V ,则称)(x V 是常正(负)的;若在D 上除0x =外总有)0(0)(<>x V ,则称)(x V 是正(负)定的;既不是常正又不是常负的函数称为变号的.定理1(零解稳定判别定理) 对系统nR x x F tx ∈=),(d d (6.7)若在区域D 上存在李雅普诺夫函数V (x )满足(1) 正定; (2)∑=∂∂=ni i iF xVt1)2.5()(d d x V 常负.则(6.7)的零解是稳定的.注意:(6.7)式中Tn x F x F x F ))(,),(()(1 =在{}K G ≤∈=x R x n|上连续,满足局部李普希兹条件,且(0)0F =.引理 若V (x )是正定(或负定)的李雅诺夫函数,且对连续有界函数()x t 有0))((lim =∞→t t x V则.0)(lim =∞→t x t定理2(零解渐近稳定判别定理) 对系统(5.2),若在区域D 上存在李雅普诺夫函数V (x )满足(1) 正定, (2)(6.7)1d ()d ni i iV tx =∂=∂∑V F x 负定,则(6.7)的零解渐近稳定.定理3(零解不稳定判别定理) 对系统(5.11)若存在李雅普诺夫函数V (x )满足(1)∑=∂∂=ni i ix F xVdtd 1)2.5()(V 正定,(2)V (x )不是常负函数, 则系统(6.7)的零解是不稳定的.。