压力容器应力分析_典型圆平板分析
- 格式:pdf
- 大小:412.66 KB
- 文档页数:31



《过程设备设计基础》教案2—压力容器应力分析课程名称:过程设备设计基础专业:过程装备与控制工程任课教师:第2章 压力容器应力分析§2-1 回转薄壳应力分析一、回转薄壳的概念薄壳:(t/R )≤0.1 R----中间面曲率半径 薄壁圆筒:(D 0/D i )max ≤1.1~1.2 二、薄壁圆筒的应力图2-1、图2-2 材料力学的“截面法”三、回转薄壳的无力矩理论1、回转薄壳的几何要素(1)回转曲面、回转壳体、中间面、壳体厚度 * 对于薄壳,可用中间面表示壳体的几何特性。
tpD td pR tpD Dt D p i 22sin 24422====⨯⎰θπθϕϕσσαασπσπ(2)母线、经线、法线、纬线、平行圆(3)第一曲率半径R1、第二曲率半径R2、平行圆半径r(4)周向坐标和经向坐标2、无力矩理论和有力矩理论(1)轴对称问题轴对称几何形状----回转壳体载荷----气压或液压应力和变形----对称于回转轴(2)无力矩理论和有力矩理论a、外力(载荷)----主要指沿壳体表面连续分布的、垂直于壳体表面的压力,如气压、液压等。
P Z= P Z(φ)b、内力薄膜内力----Nφ、Nθ(沿壳体厚度均匀分布)弯曲内力---- Qφ、Mφ、Mθ(沿壳体厚度非均匀分布)c、无力矩理论和有力矩理论有力矩理论(弯曲理论)----考虑上述全部内力无力矩理论(薄膜理论)----略去弯曲内力,只考虑薄膜内力●在壳体很薄,形状和载荷连续的情况下,弯曲应力和薄膜应力相比很小,可以忽略,即可采用无力矩理论。
●无力矩理论是一种近似理论,采用无力矩理论可是壳地应力分析大为简化,薄壁容器的应力分析和计算均以无力矩理论为基础。
在无力矩状态下,应力沿厚度均匀分布,壳体材料强度可以得到合理的利用,是最理想的应力状态。
(3)无力矩理论的基本方程a、无力矩理论的基本假设小位移假设----壳体受载后,壳体中各点的位移远小于壁厚。
考虑变形后的平衡状态时壳用变形前的尺寸代替变形后的尺寸直法线假设----变形前垂直于中面的直线变形后仍为直线,且垂直于变形后的中面。



(1)承受均布载荷时圆平板中的应力板内剪力求解:如图,选取任意位置r 处的圆平板进行受力分析,建立轴向平衡式,可求得Q r22()2r r r r Q p rpr Q Q r ππ⋅=⋅==()r r Q Q r =注意:根据图2-29(c)来确定右图中剪力的符号。
将上述边界条件代入(2-63)式中,求得)µ+最大周向弯矩出现在板的中央处,而最大径向弯矩出现在板的边缘处。
此外,弯矩为负的含义表明其方向与当初规定的方向相反(见图2-29)。
类似于上述方法,可得到挠度方程板的上(负号)、下(正号)表面的应力分布如下()()()222222338(269)33(13)8r p R r t p R r t θσµσµµ⎧=+−⎪⎪−⎨⎪⎡⎤=+−+⎣⎦⎪⎩∓∓可见,板内最大拉应力在板的下表面中央部位处。
薄圆平板应力特点①板内为两向纯弯曲应力,忽略z 方向的应力σz 和剪力Q r 引起的剪应力τ。
②板内的弯曲应力沿径向的分布形式与周边支承形式有关,工程实际中的支承形式介于固支和简支之间。
③在同等条件下,板内的最大应力要远大于薄壳内的应力,故板的厚度要比薄壳厚度大。
(2)承受集中载荷时圆平板中的应力板内剪力求解:如图,选取任意位置r 处的圆平板进行受力分析,建立轴向平衡式,可求得Q r2()2r r r r Q PP Q Q r rππ⋅===()r r Q Q r =中心开有圆形孔的圆平板称为“环板”。
以周边简支,内周边承受均布力矩的环板分析为例。
122123()0102ln 4r r Q Q r d d dw r dr r dr dr C C dw r dr r C r w r C C R ϕ==⎡⎤⎛⎞=⎜⎟⎢⎥⎝⎠⎣⎦⎧=−=+⎪⎪⎨⎪=−−+⎪⎩2.3.4 承受轴对称载荷时环板中的应力如图所示环板,须注意与上述例子的不同在于,只是边界条件有所不同。
11,,00r r r R M M r R M and w ==−===Boundary Conditions:这样,我们就可以对许多类似的问题进行求解。


第10章压力容器的弯曲应力和二次应力本章重点内容及对学生的要求:(1)掌握圆平板受均布载荷时的弯曲应力的分布规律以及对弯曲应力的限制;(2)了解边界应力的产生原因和性质以及对二次应力的限制。
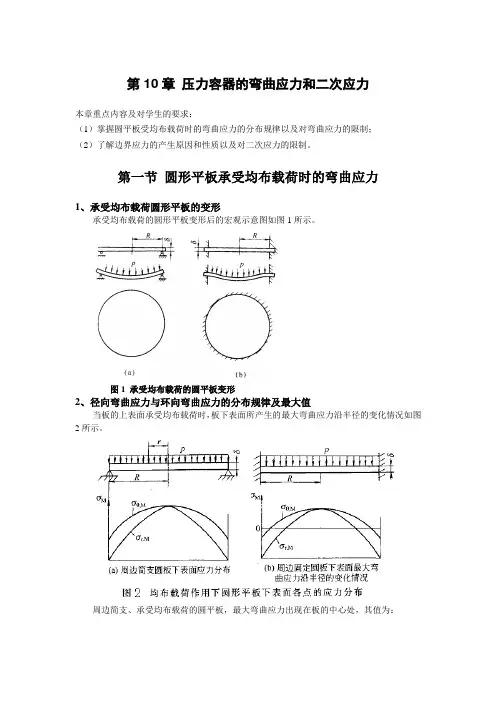
第一节圆形平板承受均布载荷时的弯曲应力1、承受均布载荷圆形平板的变形承受均布载荷的圆形平板变形后的宏观示意图如图1所示。
图1 承受均布载荷的圆平板变形2、径向弯曲应力与环向弯曲应力的分布规律及最大值当板的上表面承受均布载荷时,板下表面所产生的最大弯曲应力沿半径的变化情况如图2所示。
周边简支、承受均布载荷的圆平板,最大弯曲应力出现在板的中心处,其值为:2max ,0,023(3)()()8M r r M r pR θμσσσδ==+=== (1) 对于化工用钢,0.3μ=,则:2max 21.24pR σδ= (2)对于周边固支、承受均布载荷的圆平板,最大弯曲应力出现在板的四周,其值为: 2max 20.75pR σδ=± (3)上述公式中的“—”代表圆板上表面的应力,带“+”表示的是下表面的应力。
3、弯曲应力与薄膜应力的比较与结论上面两个式(1)与(3)可以统一为:2max 2pD K σδ= (4)其中K 为系数,对于周边简支圆平板:0.31K =;对于周边固支圆平板:0.188K =。
为了与同直径,同厚度的圆柱形壳体所产生的薄膜应力进行比较,将(4)写成:max 222D pD D K K θσσδδδ== (5) 可见圆平板的应力是圆柱体的2D K δ倍,此值非常大。
第二节圆形平板承受均布载荷时的弯曲应力1、边界应力产生的原因当设备相邻两段性能不同,或所受温度或压力不同,导致两部分变形量不同,但又相互约束,从而产生较大的剪力与弯矩。
以筒体与封头联接为例(图3),圆柱筒身与较厚的平板封头相连接在一起,承受内压时筒身要向外胀大,而平板型封头对其有一个约束作用,平板在内压下发生的是弯曲变形,直径不会增大,所以筒体与封头在连接处所出现的这种自由变形的不一致,必然导致在这个局部的边界地区产生相互约束的附加内力,即边界应力。
![圆板受力分析[策划]](https://uimg.taocdn.com/7e38f483dc88d0d233d4b14e852458fb770b38ba.webp)
第10章压力容器的弯曲应力和二次应力本章重点内容及对学生的要求:(1)掌握圆平板受均布载荷时的弯曲应力的分布规律以及对弯曲应力的限制;(2)了解边界应力的产生原因和性质以及对二次应力的限制。
第一节圆形平板承受均布载荷时的弯曲应力1、承受均布载荷圆形平板的变形承受均布载荷的圆形平板变形后的宏观示意图如图1所示。
图1 承受均布载荷的圆平板变形2、径向弯曲应力与环向弯曲应力的分布规律及最大值当板的上表面承受均布载荷时,板下表面所产生的最大弯曲应力沿半径的变化情况如图2所示。
周边简支、承受均布载荷的圆平板,最大弯曲应力出现在板的中心处,其值为:2max ,0,023(3)()()8M r r M r pR θμσσσδ==+===(1)对于化工用钢,0.3μ=,则:2max 21.24pR σδ= (2)对于周边固支、承受均布载荷的圆平板,最大弯曲应力出现在板的四周,其值为:2max 20.75pR σδ=± (3)上述公式中的“—”代表圆板上表面的应力,带“+”表示的是下表面的应力。
3、弯曲应力与薄膜应力的比较与结论上面两个式(1)与(3)可以统一为:2max 2pD Kσδ= (4)其中K 为系数,对于周边简支圆平板:0.31K =;对于周边固支圆平板:0.188K =。
为了与同直径,同厚度的圆柱形壳体所产生的薄膜应力进行比较,将(4)写成:max 222D pD DK Kθσσδδδ==(5)可见圆平板的应力是圆柱体的2DKδ倍,此值非常大。
第二节圆形平板承受均布载荷时的弯曲应力1、边界应力产生的原因当设备相邻两段性能不同,或所受温度或压力不同,导致两部分变形量不同,但又相互约束,从而产生较大的剪力与弯矩。
以筒体与封头联接为例(图3),圆柱筒身与较厚的平板封头相连接在一起,承受内压时筒身要向外胀大,而平板型封头对其有一个约束作用,平板在内压下发生的是弯曲变形,直径不会增大,所以筒体与封头在连接处所出现的这种自由变形的不一致,必然导致在这个局部的边界地区产生相互约束的附加内力,即边界应力。
(1)承受均布载荷时圆平板中的应力
板内剪力求解:
如图,选取任意位置r 处的圆平板进行受力分析,建立轴向平衡式,可求得Q r
2
2()2r r r r Q p r
pr Q Q r ππ⋅=⋅==()r r Q Q r =注意:
根据图2-29(c)来确定
右图中剪力的符号。
将上述边界条件代入(2-63)式中,求得
)µ+
最大周向弯矩出现在板的中央处,而最大径向弯矩出现在板的边缘处。
此外,弯矩为负的含义表明其方向与当初规定的方向相反(见图2-29)。
类似于上述方法,可得到挠度方程
板的上(负号)、下(正号)表面的应力分布如下
()()()222222338(269)
33(13)8r p R r t p R r t θσµσµµ⎧=+−⎪⎪−⎨⎪⎡⎤=+−+⎣⎦⎪⎩∓∓可见,板内
最大拉应力在板
的下表面中央部
位处。
薄圆平板应力特点
①
板内为两向纯弯曲应力,忽略z 方向的应力σz 和剪力Q r 引起的剪应力τ。
②板内的弯曲应力沿径向的分布形式与周边支承形式有关,工程实际中的支承形式介于固支和简支之间。
③在同等条件下,板内的最大应力要远大于薄壳内
的应力,故板的厚度要比薄壳厚度大。
(2)承受集中载荷时圆平板中的应力板内剪力求解:
如图,选取任意位置r 处的圆平板进行受力分析,建立轴向平衡式,可求得Q r
2()2r r r r Q P
P Q Q r r
ππ⋅===()r r Q Q r =
中心开有圆形孔的圆平板称为“环板”。
以周边简支,内周边承受均布力矩的环板分析为例。
122123()0
102ln 4r r Q Q r d d dw r dr r dr dr C C dw r dr r C r w r C C R ϕ==⎡⎤⎛⎞=⎜⎟⎢⎥⎝⎠⎣⎦
⎧=−=+⎪⎪⎨⎪=−−+⎪⎩
2.3.4 承受轴对称载荷时环板中的应力
如图所示环板,须注意与上述例子的不同在于,只是边界条件有所不同。
11
,,00
r r r R M M r R M and w ==−===Boundary Conditions:
这样,我们就可以对许多类似的问题进行求解。
下面举二例,并给出答案,由同学课下去做。
工程应用中的圆板受力要复杂的多,我们在解决这类实际问题时往往采用线性叠加的方法。
当然,这种线性叠加的前提是圆板受力在线弹性范围内。
2.3.5 圆板承受复杂受力求解思路
例1 周边简支内周边固支
且承受集中力P
()11
01
1220r R r R P Q R πϕϕϕ====+=
由(b)、(c)两种情形分别求出,根据其和为零,得到弯矩。
这样由
(b)、
(c)两种典型解的线性叠加,得到(a)的复杂解。
12,ϕϕ1M 例2 周边简支并承受均布载荷的环板(a)看做由(b)和(c)叠加而成,下面求M r 和Q r 。
这样,叠加图中的弯矩和剪力方向与此正好相反。
2
11
1
122122
By Eq.(2-68), when ,we find
(3)()16r r r R Q p R pR Q r R p
M R R ππµ====+−
最终的叠加方案如下图所示。
2.3 平板应力分析 2.
3.5 圆板承受复杂受力求解思路例3 法兰盘开孔接管结构。