第二章 压力容器应力分析2.4讲解

第二章压力容器应力分析Str ess Analy si s o f Pr essur e V essel s容器设计的核心问题是研究容器在各种机械载荷与热载荷作用下，有效地限制变形和抵抗破坏的能力。

因此，容器设计的理论基础就是对容器进行充分的应力和变形分析。

2．1载荷分析L oadin g An aly si s2.1.1 载荷 L oadin g（１）压力是压力容器承受的基本载荷（２）非压力载荷分整体载荷与局部载荷：整体载荷是作用于整台容器上的载荷，重力，风，地震，局部载荷是作用与容器局部区域上的载荷，管系载荷，支座反力，吊装力等．［１］重力载荷 Gravi ty［２］风载荷 Wi ndi ng［３］地震载荷 Earth qu ake［４］运输载荷 Tran sport［５］波动载荷 Un dul ate［６］管系载荷 pi pi ng（３）交变载荷2.1.2载荷工况 L oa d State(1) 正常操作工况(2) 特殊载荷工况压力试验 ,开停车及检修(3) 意外载荷工况突然停车,化学爆炸,2.2回转薄壳应力分析 Stress Analysis of Revolution Shells壳体：一种以两个曲面为界，且曲面之间距离远比其它方向尺寸小得多的构件。

壳体的中面：与壳体两曲面等距离的点所组成的曲面。

回转壳：其中面由一条平面曲线或直线绕同平面内的轴线回转而成的壳体。

壳体的厚度：二曲面之间的距离。

薄壳：厚度t/中面曲半径R 的比值101≤为薄壳，反之为厚壳。

在薄壳应力分析中，采用弹性力学薄壳理论。

几个假设：材料连续、均匀、各向同性，小变形，各层间不挤压。

受载后的变形是小变形： 壳壁各层纤维在变形后互不挤压：2.2.1薄壁圆筒的应力 Stress in Thin －ｗalled Cylinders薄壁圆筒在内压P 作用下，产生三个方向的应力 轴向应力Φσ, 周向应力θσ, 径向应力r σ 故任一点的应力状态为二向的..求解θσσ,Φ: 采用材料力学中，“截面法”保留右边，如下图（a ）根据力的平衡：内P 作用在封头上产生向右的轴向外力 24DiP π⋅在筒壁上向左的轴向内力为 Φ⋅⋅σπDt 对薄壳：D Di ≈ 故Φ=⋅σππDt DP 24得：tPD 4=Φσ取1单位长圆环，过y 轴，作上χ轴的平面，将圆环截成两半，取右半如上图（b ）。

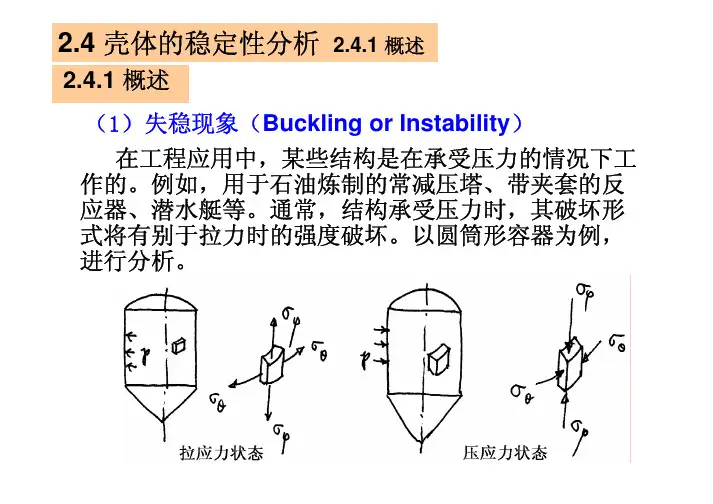
2.4 壳体的稳定性分析2.4.1 概述2.4.1 概述（1）失稳现象（Buckling or Instability） 在工程应用中，某些结构是在承受压力的情况下工 作的。

例如，用于石油炼制的常减压塔、带夹套的反 应器、潜水艇等。

通常，结构承受压力时，其破坏形 式将有别于拉力时的强度破坏。

以圆筒形容器为例， 进行分析。

2.4 壳体的稳定性分析2.4.1 概述圆筒在外压作用下，可能会有二种可能的失效形式： ① 因强度不足，导致压缩屈服失效；② 因刚度不 足，导致失稳破坏。

圆筒失稳破坏：承受外压的圆筒，当外压载荷增大到 某一值时，圆筒会突然失去原有的形状，被压瘪或出 现波纹，圆筒失去承载能力。

这种现象成为外压圆筒 的屈曲（Buckling）或失稳（Instability）。

实际上，当结构出现失稳后，最终导致结构破坏 的原因，是由于结构失稳变形后产生的附加弯矩。

下 面以杆件的失稳破坏过程进行说明。

2.4 壳体的稳定性分析2.4.1 概述2.4 壳体的稳定性分析（2）外压圆筒受载形式2.4.1 概述圆筒承受外载的形式，有以下三种：理论分析表明，在相同外载时，轴向外压对圆筒 壳体失稳的影响，要小于横向外压的影响。

本节主要 讨论横向受载失稳。

2.4 壳体的稳定性分析（3）外压圆筒失稳类型2.4.1 概述外压圆筒失稳类型有以下二种 ① 弹性失稳：圆筒为薄壁时，发生失稳时筒壁中的压 应力小于材料的屈服极限，即此时筒体的受力变形为 弹性阶段。

② 非弹性失稳：对于壁较厚的筒体，有可能在筒壁中 的应力应变进入塑性阶段后出现失稳，即此时筒体中 的压应力超过了材料的屈服点。

在本节的分析中，主要讨论弹性失稳计算。

而对 于非弹性失稳，则借助弹性失稳的结果，采用简化计 算方法。

2.4 壳体的稳定性分析（4）外压圆筒失稳形貌2.4.1 概述圆筒承受横向外载后的失稳形貌2.4 壳体的稳定性分析2.4.1 概述水下圆筒管节承受横向外载后的失稳形状2.4 壳体的稳定性分析2.4.1 概述水下圆锥形过渡管节承受横向外载后的失稳形状2.4 壳体的稳定性分析2.4.1 概述2.4 壳体的稳定性分析2.4.1 概述轴向外压圆筒的失稳形状（试验照片和计算结果）周向外压圆筒失稳后，其横截面形状如下表所示。

压力容器应力分析及其设计引言压力容器是一种用于储存或运输压力流体或气体的设备，广泛应用于化工、石油、制药等领域。

由于其工作环境的特殊性，压力容器的设计和应力分析至关重要，直接关系到设备的安全性和稳定性。

本文将介绍压力容器应力分析的基本概念和方法，并探讨压力容器设计的一些考虑因素。

压力容器应力分析在压力容器的设计和使用过程中，应力分析是非常重要的一步。

应力分析的目的是确定容器的强度和稳定性，以确保其在工作压力范围内能够安全可靠地运行。

1. 基本概念在压力容器中，由于内、外侧的压力差异，容器壁面会受到应力的作用。

应力是物体内部原子或分子间相互作用的结果，它可以表现为拉伸、压缩、剪切等形式。

常见的应力包括轴向应力、周向应力和切向应力。

轴向应力是指沿着容器轴线方向的应力，周向应力是指沿着容器周向的应力，切向应力是指垂直于容器壁面的应力。

2. 应力分析方法压力容器的应力分析可以采用数值模拟方法或者经验公式计算。

数值模拟方法通常基于有限元分析（Finite Element Analysis，简称FEA），通过划分网格、建立数学模型并求解，得到各个位置的应力值。

经验公式计算相对简便，适用于一些简单几何形状的压力容器。

常用的经验公式有ASME VIII-1标准中的公式和欧洲标准EN 13445中的公式等。

无论采用数值模拟方法还是经验公式计算，都需要考虑容器的材料特性、内外压力、温度、容器几何形状等因素。

3. 应力分析结果的评估进行应力分析后，需要对分析结果进行评估。

常见的评估指标有应力强度安全系数、应力集中系数、损伤累积等。

应力强度安全系数是指容器的实际应力值与允许应力值之间的比值。

一般要求安全系数大于1，以确保容器在额定工作条件下不会发生破坏。

应力集中系数用于评估容器上的应力集中程度。

过高的应力集中系数可能导致局部破坏和疲劳寿命的降低。

损伤累积是指容器在循环荷载作用下承受的损伤累计量。

如果损伤累积超过一定限制，容器可能发生疲劳破坏。

压力容器的应力分析摘要：压力容器是指盛装气体或者液体并承载一定压力的密闭设备，广泛应用于石油化工、能源工业、军工以及科研等各个领域。

压力容器一般由筒体、封头、法兰、密封元件、开孔和接管、支座等六大部分构成容器本体。

此外，还配有安全装置、表计及完全不同生产工艺作用的内件。

高压容器筒体与封头连接区是高压容器的高应力区之一，本文主要讨论封头和筒体之间的连接区域的应力应变情况。

一．工程背景及意义核能作为一种安全、清洁、高效以及可持续发展的能源已经为各国和各个地区广泛接受,核电是我国能源战略的重要组成组成部分之一，根据《核电中长期发展规划（2005-2020年）》，我国到2020年将实现核电装机容量4000万KW，核电占比从现在的不到2%提高到4%。

积极推进核电建设对于满足经济和社会发展不断增长的能源需求,实现能源、经济和生态环境协调发展以及提升我国综合经济实力和工业技术水平具有重要意义。

反应堆压力容器是核电厂反应堆冷却剂压力边界屏障中的一个重要设备。

它主要用来装载反应堆堆芯,密封高温、高压的冷却剂,为反应堆安全运行提供所必需的堆芯控制和堆内测量的导向和定位。

反应堆压力容器属安全一级设备,因此,要求其在各种工况下均能保持可靠的结构完整性,不会发生容器的破坏和放射性的泄漏。

筒体是压力容器的主要部件,与封头或管板共同构成承压壳体,为物料的储存,完成介质的物理、化学反应及其他工艺用途提供所必需的承压空间。

封头是保证压力容器密封的重要部件。

因此,筒体和封头的连接安全性是设计和使用中至关重要的问题,对它们进行应力评定是十分必要的。

论文以大型先进压水堆核电厂压力容器筒体及封头为研究对象，基于有限元方法,完成了反应堆压力容器筒体及封头在各种工况各种载荷组合作用下的一次应力强度的计算、分析与评定,并分析各个载荷对应力分布的影响,最终得出了结构强度符合规范要求的结论。

在此基础上,本文通过简化整体模型,创建局部模型,对筒体和封头作进一步应力评定,并将计算结果与整体模型的结果进行对比分析。

《过程设备设计基础》教案2—压力容器应力分析课程名称：过程设备设计基础专业：过程装备与控制工程任课教师：第2章 压力容器应力分析§2-1 回转薄壳应力分析一、回转薄壳的概念薄壳：（t/R ）≤0.1 R----中间面曲率半径 薄壁圆筒：（D 0/D i ）max ≤1.1~1.2 二、薄壁圆筒的应力图2-1、图2-2 材料力学的“截面法”三、回转薄壳的无力矩理论 1、回转薄壳的几何要素（1）回转曲面、回转壳体、中间面、壳体厚度tpD td pR tpD Dt D p i 22sin 24422====⨯⎰θπθϕϕσσαασπσπ* 对于薄壳，可用中间面表示壳体的几何特性。

（2）母线、经线、法线、纬线、平行圆（3）第一曲率半径R1、第二曲率半径R2、平行圆半径r（4）周向坐标和经向坐标2、无力矩理论和有力矩理论（1）轴对称问题轴对称几何形状----回转壳体载荷----气压或液压应力和变形----对称于回转轴（2）无力矩理论和有力矩理论a、外力（载荷）----主要指沿壳体表面连续分布的、垂直于壳体表面的压力，如气压、液压等。

P Z= P Z（φ）b、内力薄膜内力----Nφ、Nθ（沿壳体厚度均匀分布）弯曲内力---- Qφ、Mφ、Mθ（沿壳体厚度非均匀分布）c、无力矩理论和有力矩理论有力矩理论（弯曲理论）----考虑上述全部内力无力矩理论（薄膜理论）----略去弯曲内力，只考虑薄膜内力●在壳体很薄，形状和载荷连续的情况下，弯曲应力和薄膜应力相比很小，可以忽略，即可采用无力矩理论。

●无力矩理论是一种近似理论，采用无力矩理论可是壳地应力分析大为简化，薄壁容器的应力分析和计算均以无力矩理论为基础。

在无力矩状态下，应力沿厚度均匀分布，壳体材料强度可以得到合理的利用，是最理想的应力状态。

（3）无力矩理论的基本方程a、无力矩理论的基本假设小位移假设----壳体受载后，壳体中各点的位移远小于壁厚。

考虑变形后的平衡状态时壳用变形前的尺寸代替变形后的尺寸直法线假设----变形前垂直于中面的直线变形后仍为直线，且垂直于变形后的中面。