2014年秋季新版新人教版八年级数学上学期11.1与三角形有关的线段同步练习2

新人教版八年级数学上册《11．1 与三角形相关的线段》同步习题一、选择题1.以下表达中正确的选项是（）（A）三角形一个角的均分线与这个角的对边订交，这个角的极点与交点之间的射线，叫做三角形的角均分线。

（B）连接三角形一个极点和它对边中点的直线，叫做三角形的中线。

（C）从三角形一个极点向它的对边画垂线叫做三角形的高。

（D）三角形的三条中线总在三角形的内部。

2.三角形一边上的高（）（A）必在三角形内部（C）必在三角形的边上3.如图，AC BC 于C， CD （B）必在三角形外面（D）以上三种状况都有可能AB 于D， DE BC 于E，则以下说法中错误的是（）（A）ABC 中，AC是BC边上的高（B）BCD 中，DE是BC边上的高（C）ABE 中，DE是BE边上的高（D）ACD 中，AD是CD边上的高4.依据定义，三角形的角均分线，中线和高线都是（（A）直线（B）线段（C）射线（D）以上都对）5.假如一个三角形的三条高的交点正是三角形的一个极点，那么这个三角形是（）（A）锐角三角形（B）钝角三角形（C）直角三角形（D）不可以确立6.以下画出ABC 的高正确的选项是（）二、填空题1.如图，则图中共有 ______个三角形，它们分别是 ______；在ABD 中 B 所对的边是 ______；若BC CD DE ，则AC和AD分别是______、______的中线。

2.假如一个三角形两边上的高的交点在三角形的外面，那么这个三角形是_____三角形。

3.已知：如图， AC 为ABD 的角均分线，AE为ADF 的角均分线，则有，BAC________；DAE 1_______。

24 已.知：如图， H 是ABC 三条高AD、BE、CF的交点，则ABC 中BC边上的高是 ______，AHB 中AB边上的高是_______，HFB 中BF边上的高是________。

5.如图，AD是ABC的中线，AE是ADC的中线，则有CE______CD_____ BC。

11.1 与三角形有关的线段一、选择题（共10小题；共50分）1. 三角形按边可分为( )A. 等腰三角形、直角三角形、锐角三角形B. 直角三角形、不等边三角形C. 等腰三角形、不等边三角形D. 等腰三角形、等边三角形2. 已知a，b，c是△ABC的三边长，且(a+b+c)(a−b)=0，则△ABC一定是( )A. 等腰三角形B. 直角三角形C. 等边三角形D. 以上答案都不对3. 若钝角三角形ABC中，∠A=27∘，则下列哪个选项不可能是∠B的度数( )A. 37∘B. 57∘C. 77∘D. 97∘4. 根据定义，三角形的角平分线，中线和高线都是( )A. 直线B. 线段C. 射线D. 以上都对5. 在△ABC中，如果∠B−∠A=90∘，那么△ABC是( )A. 直角三角形B. 锐角三角形C. 钝角三角形D. 无法确定6. 已知某三角形第一条边长为(2a−b)cm，第二条边比第一条边长(a+b)cm，第三条边比第一条边的2倍少(a−b)cm，则这个三角形的周长为( )A. 3a cmB. (3a−b)cmC. (5a−b)cmD. (8a−2b)cm7. 如图，工人师傅做了一个长方形窗框ABCD，E，F，G，H分别是四条边上的中点，为了使它稳固，需要在窗框上钉一根木条，这根木条不应钉在( )A. A，C两点之问B. E，G两点之间C. B，F两点之间D. G，H两点之间8. 人字梯中间一般会设计一“拉杆”，这样做的道理是( )A. 两点之间，线段最短B. 垂线段最短C. 两直线平行，内错角相等D. 三角形具有稳定性9. 如图，在Rt△ABC中，∠C=90∘，以△ABC的一边为边画等腰三角形，使得它的第三个顶点在△ABC的其他边上，则可以画出的不同的等腰三角形的个数最多为( )A. 4B. 5C. 6D. 710. 已知三角形的两边长分别为4cm和9cm，则下列长度的四条线段中能作为第三边的是( )A. 13cmB. 6cmC. 5cmD. 4cm二、填空题（共6小题；共48分）11. 如果知道三角形的一边之长和这边上的高，三角形确定．（填“能”或“不能”）12. 三角形按边分类：三角形{三边都不等的三角形等腰三角形{ 的等腰三角形 的三角形13. 如图，在锐角三角形ABC中，AD⊥BC于点D，E是BC上一点，连接AE．图中：（1）锐角三角形有个；（2）直角三角形有个；（3）钝角三角形有个．14. 等腰三角形的、、三线合一．15. 如果等腰三角形的底边和一腰长分别为12cm，15cm．那么这个三角形的周长为cm．16. 如图，用六根木条钉成一个六边形框架ABCDEF，要使框架稳固且不活动，则至少还需要添加根木条．三、解答题（共4小题；共52分）17. 图中有几个不同的三角形?用符号表示这些三角形．18. 用9根同样的火柴棒在桌面上摆一个三角形（应首尾相接，不允许火柴棒折断，但允许将几根火柴棒连成一根作为一条线段，火柴要全部用完），你能摆出哪几种不同形状的三角形?19. 已知△ABC中两个内角的度数，判断△ABC的类型：（1）∠A=30∘，∠B=40∘．（2）∠B=32∘，∠C=58∘．（3）∠A=60∘，∠C=50∘．20. 为使五边形木架（用5根木条钉成）不变形，哥哥准备如图①那样再钉上两根木条，弟弟准备如图②那样再钉上两根木条，哪种方法能使木架不变形?为什么?答案第一部分1. C2. A3. C 【解析】∵钝角三角形△ABC中，∠A=27∘，∴∠B+∠C=180∘−27∘=153∘，又∵△ABC为钝角三角形，有两种可能情形如下：① ∠C>90∘，∴∠B<153∘−90∘=63∘，∴选项A，B合理；② ∠B>90∘，∴选项D合理，∴∠B不可能为77∘．4. B 【解析】三角形的角平分线，中线和高线都是线段．5. C6. D7. B8. D 【解析】人字梯中间一般会设计一“拉杆”，是为了形成三角形，利用三角形具有稳定性来增加其稳定性．故选：D．9. D10. B第二部分11. 不能【解析】画出简图比较容易判定．如图，知道三角形的一边之长和这边上的高，三角形不能确定．12. 底边和腰不相等，等边13. 2，3，114. 顶角平分线，底边上的中线，底边上的高15. 4216. 3第三部分17. △ABE，△BCE，△CDE，△ABC，△BCD．18. 三种（3，3，3；3，4，2；1，4，4）．19. （1）钝角三角形．（2）直角三角形．（3）锐角三角形．20. 两种方法都能使木架不变形．在图①中，△ABE，△BDE，△BCD的形状和大小不变．在图②中，△ABE，△ABC的形状和大小不变，故点D相对△ABE，△ABC的位置也不变．。

新人教版八年级数学上册《11.1 与三角形相关的线段》同步练习
三角形两边的和，三角形两边的差。

三角形的高、中线与角均分线都是，能够胸怀它们的大小。

拥有稳固性，而四边形不具有。

练习：
1、三角形的三边长分别是4、 7、 x，则 x 的取值范围是它的周长的取值范围是
2、已知等腰三角形的两边长分别是4cm 和 5cm，则它的周长是，若它的两边长分别是4cm和 9cm，则它的周长是。

3、有 5 条线段分别长为1cm、 2cm、 3cm、 4cm、 5cm，则以此中 3 条线段为边能够组成个三角形。

4、在下边三个三角形中分别画出它的三条高、三条中线、三条角均分线，并写出图中相等
的线段或角。

A
A
A
C
C
C
B
B B
5、要使一个五边形拥有稳固性，则需起码增添条对角线。

6、已知直角三角形的三边长为 3 cm、 4cm、 5cm，那么它的斜边上的高为cm。

11.2 与三角形相关的角
三角形内角和定理：
推论： 1、直角三角形的；
2、有三角形是直角三角形；
3、三角形的外角等于。

5、如图，∠B=42°，∠ A+10° =∠ 1,∠ ACD=64°证明：AB∥ CD
C
D
1
A B
6、如图， AB∥CD，∠ B = 72 °，∠ D = 32 °，求∠ F 的度数。

第11章 第11.1节 与三角形有关的线段 同步练习一一．填空题 1．如图所示（1）图中共有 个三角形， 分别是 ；（2）△ABC 的三个顶点是 ； 三个内角是 ；（3）∠B 是哪些三角形的内角 ；（4）AC 是哪些三角形的边 ；（5）∠B 是 △ABC ，△ABE ，△DBC 中 、 、 边的对角；（6）AC 分别是△AOC ，△ADC ，△AEC ，△ABC 中 ∠ 、∠ 、∠ 、 ∠ 的对边.2．若三角形的两边长分别是4cm 和5cm ，第三边的长为xcm ，则x 的取值范围是 .二．选择题1．以下列各组线段为边，能组成三角形的是（ ）A.1cm, 2cm, 4cmB.8cm, 6cm, 4cmC.12cm, 5cm, 6cmD.2cm, 3cm, 6cm2．现有两根木棒，它们的长度分别是20cm 和30cm ，若不改变木棒的长度，要钉成一个三角形，则应在下列四根木棒中选取( )A.10cm 的木棒B.20cm 的木棒C.50cm 的木棒D.60cm 的木棒3. 一个三角形的两边长分别是3和6，第三边的长为奇数，那么第三边的长是（ ）A.5或7B.7或9C.3或5D.9三．解答题1. 小明制作一个三角形铁丝架，现在有两根铁丝，长度分别是3cm 和5cm ，（1）小明如何选用第三根铁丝，能确定它的长度吗？能确定它的长度范围吗？（2）如果第三根铁丝的长度要求是整数，小明有几种选择？2. 五条线段长分别是1cm 、2cm 、3cm 、4cm 、5cm 以其中三条线段为边长组成1题图C三角形，有几种选法？为什么？3. 一个三角形有两条边相等，周长为16cm，三角形的一边长4cm，求其它两边长.答案一、填空题1、（1）8, △ABC, △ABE, △ADO, △ADC, △BDC, △AOC, △△BEA, △EOC(2)点A,点B,点C, ∠B, ∠BAC, ∠ACB （3）△ABE，△BDC，△ABC（4）△AEC，△ADC，△ABC，△AOC （5）AC，AE，DC（6）∠AOC，∠ADC，∠AEC，∠ABC2、1＜x＜9二．选择题1、B2、B3、A三．解答题1、（1）不能确定它的长度，可以确定它的长度范围为：2cm＜x＜8cm(2)小明可以有五种选择，选择长度分别为3cm,4cm,5cm,6cm,7cm2、有3中选法可以组成三角形，分别为:①2cm,3cm,4cm②3cm,4cm,5cm③2cm,4cm,5cm3、6cm和4cm良好的学习态度能够更好的提高学习能力。

第11章《三角形》同步练习（§11.1 与三角形有关的线段A）班级学号姓名得分1、填空题：(1)由____________三条线段______所组成的图形叫做三角形．组成三角形的线段叫做______；相邻两边的公共端点叫做______，相邻两边所组成的角叫做______，简称______．(2)如图所示，顶点是A、B、C的三角形，记作______，读作______．其中，顶点A所对的边______还可用______表示；顶点B所对的边______还可用______表示；顶点C 所对的边______还可用______表示．(3)由“连接两点的线中，线段最短”这一性质可以得到三角形的三边有这样的性质______________________________．由它还可推出：三角形两边的差____________．(4)对于△ABC，若a≥b，则a＋b______c同时a－b______c；又可写成______＜c＜______．(5)若一个三角形的两边长分别为4cm和5cm，则第三边x的长度的取值范围是____________，其中x可以取的整数值为____________．2．已知：如图，试回答下列问题：(1)图中有______个三角形，它们分别是______________________________________.(2)以线段AD为公共边的三角形是_________________________________________.(3)线段CE所在的三角形是______，CE边所对的角是________________________．(4)△ABC、△ACD、△ADE这三个三角形的面积之比等于______∶______∶______．3．选择题：(1)下列各组线段能组成一个三角形的是( )．(A)3cm，3cm，6cm (B)2cm，3cm，6cm(C)5cm，8cm，12cm (D)4cm，7cm，11cm(2)现有两根木条，它们的长分别为50cm，35cm，如果要钉一个三角形木架，那么下列四根木条中应选取( )．(A)0.85m长的木条(B)0.15m长的木条(C)1m长的木条(D)0.5m长的木条(3)从长度分别为10cm、20cm、30cm、40cm的四根木条中，任取三根可组成三角形的个数是( )．(A)1个(B)2个(C)3个(D)4个(4)若三角形的两边长分别为3和5，则其周长l的取值范围是( )．(A)6＜l＜15 (B)6＜l＜16(C)11＜l＜13 (D)10＜l＜164.(1)一个等腰三角形的周长为18，若腰长的3倍比底边的2倍多6，求各边长．(2)已知等腰三角形的一边等于8cm，一边等于6cm，求它的周长．(3)一个等腰三角形的周长为30cm，一边长为6cm，求其它两边的长．(4)有两边相等的三角形的周长为12cm，一边与另一边的差是3cm，求三边的长．5．(1)若三角形三条边的长分别是7，10，x，求x的范围．(2)若三边分别为2，x－1，3，求x的范围．(3)若三角形两边长为7和10，求最长边x的范围．(4)等腰三角形腰长为2，求周长l的范围．(5)等腰三角形的腰长是整数，周长是10，求它的各边长．6．已知：如图，△ABC中，AB＝AC，D是AB边上一点．(1)通过度量AB 、CD 、DB 的长度，确定AB 与)(21DB CD 的大小关系.(2)试用你所学的知识来说明这个不等关系是成立的．7．已知：如图，P 是△ABC 内一点．请想一个办法说明AB ＋AC ＞PB ＋PC ．8．如图，D 、E 是△ABC 内的两点，求证：AB ＋AC ＞BD ＋DE ＋EC ．第11章《三角形》同步练习（§11.1 与三角形有关的线段B ）班级 学号 姓名 得分1．填空题：(1)从三角形一个顶点向它的对边画______，以______和______为端点的线段叫做三角形这边上的高．如图，若CD 是△ABC 中AB 边上的高，则∠ADC ______∠BDC ＝______，C 点到对边AB 的距离是______的长．(2)连结三角形的一个顶点和它______的______叫做三角形这边上的中线． 如右图，若BE 是△ABC 中AC 边上的中线，则AE ______.______21EC(3)三角形一个角的______与这个角的对边相交，以这个角的______和______为端点的线段叫做三角形的角平分线．一个角的平分线与三角形的角平分线的区别是________________________________ ______________________________________． 如图，若AD 是△ABC 的角平分线，则∠BAD ______∠CAD ＝21______或∠BAC ＝2______＝2______．2．已知：△GEF ，分别画出此三角形的高GH ，中线EM ，角平分线FN ．3．(1)分别画出△ABC 的三条高AD 、BE 、CF ．(∠A为锐角) (∠A为直角) (∠A为钝角)(2)这三条高AD、BE、CF所在的直线有怎样的位置关系?4．(1)分别画出△ABC的三条中线AD、BE、CF．(2)这三条中线AD、BE、CF有怎样的位置关系?(3)设中线AD与BE相交于M点，分别量一量线段BM和ME、线段AM和MD的长，从中你能发现什么结论?5．(1)分别画出△ABC的三条角平分线AD、BE、CF.(2)这三条角平分线AD、BE、CF有怎样的位置关系?(3)设△ABC的角平分线BE、CF交于N点，请量一量点N到△ABC三边的距离，从中你能发现什么结论?6．已知：△ABC中，AB＝AC，BD是AC边上的中线，如果D点把三角形ABC的周长分为12cm和15cm两部分，求此三角形各边的长．7．(1)如果将一个三角形的三边的长确定，那么这个三角形的形状和大小就不会改变了，三角形的这个性质叫做________________________. (2)四边形是否具有这种性质? 8．将一个三角形剖分成若干个面积相等的小三角形，称为该三角形的等积三角形的剖分(以下两问要求各画三个示意图)(1)已知一个任意三角形，并其剖分成3个等积的三角形． (2)已知一个任意三角形，将其剖分成4个等积的三角形．9．不等边△ABC 的两条高长度分别为4和12，若第三条高的长也是整数，试求它的长．参考答案（§11.1 与三角形有关的线段A ）1．(1)不在同一直线上的，首尾顺次相接，三角形的边，三角形的顶点，三角形的内角，三角形的角．(2)△ABC ，三角形ABC ，BC ，a ；AC ，b ；AB ，c (3)三角形两边之和大于第三边，小于第三边． (4)＞，＜，a －b ，a ＋b(5)1cm ＜x ＜9cm ，2cm 、3cm 、4cm 、5cm 、6cm 、7cm 、8cm ． 2．(1)六，△ABC 、△ABD 、△ABE 、△ACD 、△ACE 、△ADE ． (2)△ABD 、△ACD 、△ADE ． (3)△ACE ，∠CAE ． (4)BC ：CD ：DE ．3．(1)C ，(2)D ，(3)A ，(4)D4．(1)6，6，6；(2)20cm ，22cm ；(3)12cm ，12cm ；(4)5cm ，5cm ，2cm ． 5．(1)3＜x ＜17；(2)2＜x ＜6；(3)10≤x ＜17；(4)4＜e ＜8； (5)3，3，4或4，4，2 6．(1))(21DB CD AB +>． (2)提示：对于△ADC ，∵AD ＋AC ＞DC ， ∴(AD ＋DB )＋AC ＞CD ＋DB ， 即AB ＋AC ＞CD ＋DB ．又∵AB ＝AC ，∴2AB ＞CD ＋DB ． 从而AB ＞21(CD ＋DB )． 7．提示：延长BP 交AC 于D ．∵在△ABD 中，AB ＋AD ＞BD ＝BP ＋PD ，① 在△DPC 中，DP ＋DC ＞PC ，② 由①、②，∴AB ＋(AD ＋DC )＋DP ＞BP ＋PC ＋DP ． 即AB ＋AC ＞PB ＋PC ．8．证明：延长BP 交AC 于D ，延长CE 交BD 于F ． 在△ABD 中，AB ＋AD ＞BD ． ① 在△FDC 中，FD ＋DC ＞FC ． ② 在△PEF 中，PF ＋FE ＞PE ． ③①＋②＋③得AB ＋AD ＋FD ＋DC ＋PF ＋FE ＞BD ＋FC ＋PE ， 即：AB ＋AC ＋PF ＋FD ＋FE ＞BP ＋PF ＋FD ＋FE ＋EC ＋PE ， 所以AB ＋AC ＞BP ＋PE ＋EC ．（§11.1 与三角形有关的线段B ）1．(1)垂线，顶点、垂足，＝，90°，高CD 的长． (2)所对的边的中点、线段，＝，AC(3)平分线，顶点、交点，一个角的平分线是射线，而三角形的角平分线是线段． ＝，∠BAC ，∠BAD ，∠DAC 2．略．3．(1)略，(2)三条高所在直线交于一点．4．(1)略，(2)三条中线交于一点，(3)BM ＝2ME ．5．(1)略，(2)三条角平分线交于一点，(3)点N 到△ABC 三边的距离相等． 6．提示：有两种情况，分别运用方程思想，设未知数求解．⎩⎨⎧===,11,8BC AC AB 或⎩⎨⎧===.7,10BC AC AB 7．(1)三角形的稳定性，(2)不具有稳定性．8．(1)(2)下列各图是答案的一部分：9．它的长为5，或4．提示：设S △ABC ＝S ，第三条高为h ，则△ABC 的三边长可表示为：hSS S 212242、、，列不等式得：12242212242SS h S S S +<<- ∴3＜h ＜6．。

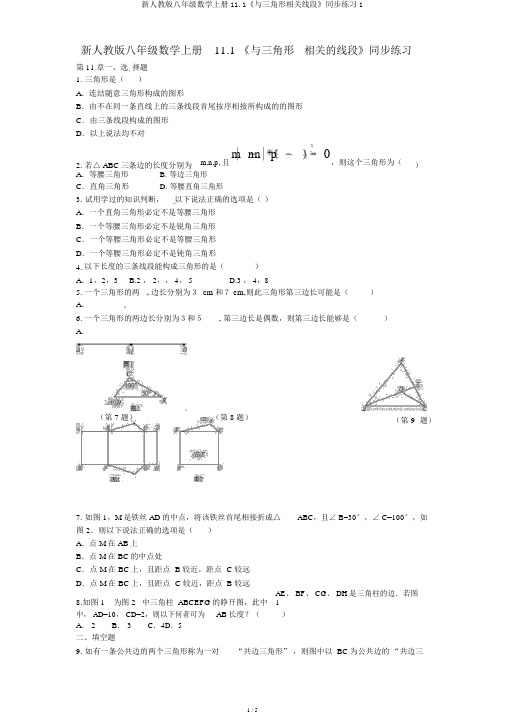
新人教版八年级数学上册11.1 《与三角形相关的线段》同步练习第11章一、选择题1. 三角形是（）A．连结随意三角形构成的图形B．由不在同一条直线上的三条线段首尾按序相接所构成的的图形C．由三条线段构成的图形D．以上说法均不对m,n,p, 且m nn p22. 若△ ABC三条边的长度分别为0，则这个三角形为（）A．等腰三角形 B. 等边三角形C．直角三角形 D. 等腰直角三角形3. 试用学过的知识判断，以下说法正确的选项是（）A．一个直角三角形必定不是等腰三角形B．一个等腰三角形必定不是锐角三角形C．一个等腰三角形必定不是等腰三角形D．一个等腰三角形必定不是钝角三角形4.以下长度的三条线段能构成三角形的是（）A．1，2，3 B.2 ， 2，， 4， 5 D.3 ， 4，85.一个三角形的两边长分别为３ cm和７ cm,则此三角形第三边长可能是（）A．6.一个三角形的两边长分别为３和５, 第三边长是偶数，则第三边长能够是（）A．（第 7题）（第 8题）（第 9题）7. 如图 1，M是铁丝 AD的中点，将该铁丝首尾相接折成△ABC，且∠ B=30°，∠ C=100°，如图 2．则以下说法正确的选项是（）A．点 M在 AB上B．点 M在 BC的中点处C．点 M在 BC上，且距点 B 较近，距点 C 较远D．点 M在 BC上，且距点 C 较近，距点 B 较远8.如图 1为图 2中三角柱 ABCEFG的睁开图，此中AE、 BF、 CG、 DH是三角柱的边．若图1中， AD=10， CD=2，则以下何者可为AB长度？（）A． 2B． 3C．4D．5二、填空题9. 如有一条公共边的两个三角形称为一对“共边三角形”，则图中以 BC为公共边的“共边三角形”有 ________对10.已知△ ABC的一个外角为 50°，则△ ABC必定是 ________ 三角形 .11.若等腰三角形两边长分别为３和５，则它的周长是_______________.12.如图，Ｃ在三角形中所对的边是________________.13.用７根火柴首尾按序相接摆成一个三角形，能摆成_______个不一样的三角形 .14.如图，在图１中互不重叠的三角形共有４个，在图２中，互不重叠的三角形共有７个，在图３中，互不重叠的三角形共有１０个,, 则在第n 个图形中，互不重叠的三角形共有__________个（用含n 的代数式表示）.15. 用 12 根火柴棒（等长）拼成一个三角形，火柴棒不一样意节余，重不一样的三角形的个数有_ _________ ．16. 如图，图 1 中共有 3 个三角形，图 2 中共有 6 个三角形，图以此类推，则图 6 中共有 __________个三角形．叠和折断，则能摆出3 中共有 10 个三角形， , ，17. 如图，直角 ABC的周长为的周长为__________ ．2008，在其内部有五个小直角三角形，则这五个小直角三角形18. 平面上有 5 个点，此中随意三点都不在同一条直线上，则这些点共可构成__________ 个不一样的三角形．三、解答题19.两条平行直线上各有 n 个点，用这 n 对点按以下的规则连结线段；①平行线之间的点在连线段时，能够有共同的端点，但不可以有其余交点；②切合①要求的线段一定所有画出；图 1 展现了当n=1 时的状况，此时图中三角形的个数为0；图 2 展现了当 n=2 时的一种状况，此时图中三角形的个数为2；（ 1）当n=3 时，请在图 3 中画出使三角形个数最少的图形，此时图中三角形的个数为__________个；（2）试猜想当 n 对点时，按上述规则画出的图形中，最罕有多少个三角形？（3）当 n=2006 时，按上述规则画出的图形中，最罕有多少个三角形？20.过 A、 B、 C、 D、E 五个点中随意三点画三角形；（1）此中以 AB为一边能够画出 __________ 个三角形；（2）此中以 C 为极点能够画出 __________ 个三角形．21.如图，△ ABC是某村一遍若干亩土地的表示图，在党的“十六大”精神的指导下，为进一步加大乡村经济构造调整的力度，某村决定把这块土地均匀分给四位“花农”栽种，请你帮他们分一分，供给两种分法．要求：画出图形，并简要说明分法．22. 如图，△ ABC中， A1， A2， A3，, ， An 为 AC边上不一样的n 个点，第一连结BA1，图中出现了 3 个不一样的三角形，再连结BA2，图中便有 6 个不一样的三角形,（1）达成下表：连结个数出现三角形个数若出现了45 个三角形，则共连结了多少个点？若向来连结到An，则图中共有 __________ 个三角形．23.一个三角形三边长之比为 2： 3： 4，周长为 36cm，求此三角形的三边长．第 11 章—— 11.1 《与三角形相关的线段》同步练习二、填空题9.3 10.钝角11.1 1 或 13 12.ＡＥ,ＢＤ,ＡＢ三、解答题19.解：（ 1）4个；（2）当有 n 对点时，最少能够画2（ n-1 ）个三角形；（3） 2×（ 2006-1 ） =4010 个．答：当 n=2006 时，最少能够画4010 个三角形．20.解：（ 1）如图，以 AB为一边的三角形有△ ABC、△ ABD、△ ABE共 3 个；（2）如图，以点 C 为极点的三角形有△ABC、△ BEC、△ BCD、△ ACE、△ ACD、△ CDE共 6个．故答案为：（ 1）3，（ 2） 6．21.解：第一种是取各边的中点，分别取， AB．BC，AC的中点 D，E， Y，连结 DE，EY和 AE，所形成的四个三角形面积相等（以以下图）．第二种，在 BC边上取四平分点 D，E， F，分别连结 AD， AE，AF，所形成的四个三角形面积相等（以以下图）．22.解：（ 1）连结个数123456出现三角形个数3610152128（2） 8 个点；1 ( n 1)(n 2)（3） 1+2+3+, +（ n+1)=223.解：设三边长分别为 2x，3x， 4x，由题意得， 2x+3x+4x=36 ，解得： x=4．故三边长为： 8cm， 12cm， 16cm．。

11.1 与三角形有关的线段知识要点：1.三角形概念：由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形．2.定理：三角形任意两边之和大于第三边，三角形任意两边之差小于第三边.3.三角形的高：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段叫做三角形的高线，简称三角形的高．4.三角形的中线：三角形的一个顶点与它的对边中点的连线叫三角形的中线．5.三角形的角平分线：三角形的一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线．6. 如果三角形的三边固定，那么三角形的形状大小就完全固定了，这个性质叫做三角形的稳定性.一、单选题1．下列每组数分别表示三根木棒的长，将它们首尾连接后，能摆成三角形的一组是（）A．2，2，4 B．3，2，6 C．1，2，2 D．1，2，32．下列四个图形中，线段是的高的是（）A. B.C. D.3．下列各组数中，不可能成为一个三角形三边长的是（ ）A.5，6，12B.2，3，4C.5，7，7D.6，8，10 4．周长为 20，边长为整数的三角形有（ ）个A ．6B ．7C ．8D ．95．已知等腰三角形的两边长分别为6cm ，3cm ，则该等腰三角形的周长是( ) A ．9cm B ．12cm C ．12cm 或者15cm D ．15cm6．如图，在△ABC 中，AD 和BE 是角平分线，其交点为O ，若∠BOD =66°， 则∠ACB 的度数（ ）A ．33°B ．28°C ．52°D ．48°7．如图，在ABC ∆中，E 是边BC 上点，2EC BE =，点D 是AC 的中点。

连接AE ，BD 交于F ，已知6ABC S ∆=，则ADF BEF S S ∆∆-=（ ）A ．1B ．2C ．3D ．48．下列说法中错误的是（）A．三角形三条角平分线都在三角形的内部B．三角形三条中线都在三角形的内部C．三角形三条高至少有一条在三角形的内部D．三角形三条高都在三角形的内部9．如图，在长方形网格中，每个小长方形的长为2，宽为1，A、B两点在网格格点上，若点C也在网格格点上，以A、B、C为顶点的三角形面积为2，则满足条件的点C个数是（）A．2 B．3C．4 D．510．一个三角形的两边分别是3和8，而第三边的长为奇数，则第三边的长是（）A．3或5 ；B．5或7；C．7或9；D．9或11二、填空题11．若一个三角形的两边长为3和5，且周长为偶数，则这个三角形的第三边长为_____．12．若从长度分别为3cm、4cm、7cm和9cm的小木棒中任选取3根搭成了一个三角形，则这个三角形的周长为__________．a ，4，则a的取值范围为________________；13．若三角形的三边长分别为2，114．如图，直线AB ，CD 相交于点O ，若∠EOC ：∠EOD=4 ：5 ，OA平分∠EOC ，则∠BOE=___________．15．如图，在△ABC 中，已知点D 、E 、F 分别为BC 、AD 、CE 的中点，且S △ABC ＝4cm 2，则S △BEF =_________三、解答题16．如图，AD ，CE 是△ABC 的两条高；已知AD ＝10，CE ＝9，AB ＝12.(1)求△ABC 的面积；(2)求BC 的长.17．已知：如图，点C 在AOB ∠的一边OA 上，过点C 的直线//DE OB ，CF 平分ACD ∠，CG CF ⊥于C .()1若40O ∠=，求ECF ∠的度数；()2求证:CG 平分OCD ∠；18．已知三角形三边长为a 、b 、c ，且-+--a b c a b c += 10，求b 的值 答案一、单选题1．C2．D3．A4．C5．D6．D7．A8．D9．C10．C二、填空题11．4或612．19cm或20cm13．3＜a＜714．140°15．1三、解答题16．(1)S△ABC＝AB·CE＝×12×9＝54.(2)因为S△ABC＝BC·AD，所以×10×BC＝54.所以BC＝.点睛：三角形的面积等于它的底和底上的高和积的一半，设a，b，c边上的高分别为h a，h b，h c，则有ah a＝bh b＝ch c.17．解：（1）∵DE∥OB，∴∠O=∠ACE，（两直线平行，同位角相等）∵∠O=40°，∴∠ACE=40°，∵∠ACD+∠ACE=180°，（平角定义）∴∠ACD=140°，又∵CF平分∠ACD，∴∠ACF=70°，（角平分线定义）∴∠ECF=70°+40°=110°；（2）证明：∵CG⊥CF，∴∠FCG=90°，∴∠DCG+∠DCF=90°，又∵∠AOC=180°，（平角定义）∴∠GCO+∠FCA=90°，∵∠ACF=∠DCF ，∴∠GCO=∠GCD ，（等角的余角相等）即CG 平分∠OCD ．18．b=5解：∵a 、b 、c 是三角形的三边长，∴a+b ＞c ，a−b ＜c ， ∴-+--()210a b c a b c a b c a b c a b c a b c b +=+----=+--++==， ∴b=5.。

11.1与三角形有关的线段同步基础训练二一、填空题1、(1)从三角形一个顶点向它的对边画__________ ，以______ 和______ 为端点的线段叫做三角形这边上的高.如图，若CD是厶ABC中AB边上的高，则/ ADC ________ /BDC = _________ , C点到对边AB的距离是 ______ 的长.(2)______________________________ 连结三角形的一个顶点和它的叫做三角形这边上的中线.1如右图，若BE是厶ABC中AC边上的中线，则AE _________ E C二________2(3)____________________ 三角形一个角的 __________________________ 与这个角的对边相交，以这个角的和为端点的线段叫做三角形的角平分线.一个角的平分线与三角形的角平分线的区别是_____________________________________________ .1如图，若AD是厶ABC的角平分线，则/ BAD ________ /CAD = 或/ BAC = 2 = 2 .22、已知：△ GEF，分别画出此三角形的高GH，中线EM，角平分线FN .3、任意一个三角形都有一条角平分线，条中线，条咼线.4、△ ABC的高BD垂至于边 _______ ，角平分线AE平分__________ ，中线CF平分边___________ .5、如图：(1) AD丄BC,垂足为D，贝U AD是_____ 边上的高，/ __________ =Z ________ =90 °1 /(2)AE 平分/ BAC,交BC 于 E 点，贝U AE 叫________ ，/ ______ =Z _______ = - / _________(3)___________________________________ 若AF = FC,UA ABC 的中线是 , 0ABF= .(4)______________________________ 若BG = GH = HF，贝U AG是的中线，AH是的中线.6、如图：已知AB丄AC, AB是厶ABC的边_____ 上的高，也是△ BDC的边 ______ 上的高，也是△ ABD的边________ 上的高。

第11章——11.1《与三角形 有关的线段》同步练习及（含答案）一、选择题1.画△ABC 中AB 边上的高，下列画法中正确的是（ ）A．B． C． D．2．下列说法正确的是（ ）A ．三角形三条高都在三角形内B ．三角形三条中线相交于一点C ．三角形的三条角平分线可能在三角形内，也可能在三角形外D ．三角形的角平分线是射线3.如图，已知BD 是△ABC 的中线，AB=5，BC=3，△ABD 和△BCD 的周长的差是（ ）A ．2B ．3C ．6D ．不能确定4.如图，△ABC 中∠C=90°，CD ⊥AB ，图中线段中可以作为△ABC 的高的有（ ） A ．2条 B ．3条 C ．4条 D ．5条5．在△ABC 中，AD 为中线，BE 为角平分线，则在以下等式中：①∠BAD=∠CAD ；②∠ABE=∠CBE ；③BD=DC ；④AE=EC ．正确的是（ ）A ．①②B ．③④C ．①④D ．②③6.（2011•绵阳）王师傅用4根木条钉成一个四边形木架，如图．要使这个木架不变形，他至少还要再钉上几根木条？（ ）A ．0根B ．1根C ．2根D ．3根7.（2006•绵阳）如图，工人师傅砌门时，常用木条EF 固定矩形门框ABCD ，使其不变形，这种做法的根据是（ ）A ．两点之间线段最短B ．矩形的对称性C ．矩形的四个角都是直角D ．三角形的稳定性8.三角形的高线是（ ）A ．直线B ．线段C ．射线D ．三种情况都可能二、填空题9.如图，在△ABC 中，∠ACB=90°，CD ⊥AD ，垂足为点D ，有下列说法： ①点A 与点B 的距离是线段AB 的长；（第3题） （第4题） （第6题） （第7题）②点A 到直线CD 的距离是线段AD 的长；③线段CD 是△ABC 边AB 上的高；④线段CD 是△BCD 边BD 上的高．上述说法中，正确的个数为_________个10.如图，△ABC 的角平分线AD 、中线BE 相交于点O ，则①AO 是△ABE 的角平分线；②BO 是△ABD 的中线；③DE 是△ADC 的中线；④ED 是△EBC 的角平分线的结论中正确的有_________.11．（2004•新疆）如图，小明的父亲在院子的门板上钉了一个加固板，从数学角度看，这样做的原因是______________________．12.如图所示，CD 是△ABC 的中线，AC=9cm ，BC=3cm ，那么△ACD 和△BCD 的周长差是___________cm ．13.AD 是△ABC 的一条高，如果∠BAD=65°，∠CAD=30°，则∠BAC=______．14.如图，在△ABC 中，AC ⊥BC ，CD ⊥AB 于点D ．则图中共有_____个直角三角形．15.如图，在△ABC 中，BD 是角平分线，BE 是中线，若AC=24cm ，则AE=cm ，若∠ABC=72°，则∠ABD=_____度．16.如图所示：（1）在△ABC 中，BC 边上的高是_____；（2）在△AEC 中，AE 边上的高是_____．17.三角形一边上的中线把三角形分成的两个三角形的面积关系为_____.18.如图，在△ABC 中，CD 平分∠ACB ，DE ∥AC ，DC ∥EF ，则与∠ACD 相等角有_____个．三、解答题19．如图，AD 是△ABC 的角平分线，过点D 作直线DF ∥BA ，交△ABC 的外角平分线AF 于点F ，DF 与AC 交于点E ．求证：DE=EF ．（第18题）（第16题） （第9题）（第10题）（第19题） （第11题）（第12题）（第14题）（第15题）20.若等腰三角形一腰上的中线分周长为１２cm 和１５cm 两部分，求这个等腰三角形的底边和腰的长.21. 如图：（1）画出△ABC 的BC 边上的高线AD ； （2）画出△ABC 的角平分线CE ．22.△ABC 中，AD ⊥BC ，AE 平分∠BAC 交BC 于点E ．（1）∠B=30°，∠C=70°，求∠EAD 的大小．（2）若∠B ＜∠C ，则2∠EAD 与∠C-∠B 是否相等？若相等，请说明理由．23.已知△ABC 中，∠ACB=90°，CD 为AB 边上的高，BE 平分∠ABC ，分别交CD 、AC 于点F 、E ，求证：∠CFE=∠CEF ．第21题第22题 第23题第11章——11.1《与三角形 有关的线段》同步练习及（含答案）一、选择题1.C2.B3.A4.B5.D6.B7.D8.B二、填空题9.4 10.2 11.利用三角形的稳定性使门板不变形． 12..6 13.95°或35° 14.3 15.12,36 16.AB,CD 17.相等 18.4三、解答题19.证明：∵AD 是△ABC 的角平分线，AF 平分△ABC 的外角，∴∠1=∠2，∠3=∠4，∵DF ∥BA ，∴∠4=∠ADE ，∠1=∠F∴∠3=∠ADE ，∠2=∠F∴DE=EA EF=EA∴DE=EF20.在ＡＢＣ∆中，ＡＢ＝ＡＣ，ＢＤ是中线，设ＡＢ＝x,BC=y .(1)当AB+AD=12时，则⎪⎪⎩⎪⎪⎨⎧=+=+15211221x y x x ，解得,118⎩⎨⎧==y x ∴三角形三边的长为８，８，１１； （２）当AB+AD=1５时，则⎪⎪⎩⎪⎪⎨⎧=+=+12211521x y x x ，解得,y x ⎩⎨⎧==710∴三角形三边的长为１０，１０，７； 经检验，两种情况均符合三角形的三边关系.∴三角形三边的长分别为８，８，１１或１０，１０，７.21. 解：（1）如图所示：AD 即为所求；（2）如图所示：CE 即为所求．22.解：（1）∵∠B=30°，∠C=70°∴∠BAC=180°-∠B-∠C=80°∵AE 是角平分线， ∴∠EAC=21∠BAC=40° ∵AD 是高，∠C=70°∴∠DAC=90°-∠C=20°∴∠EAD=∠EAC-∠DAC=40°-20°=20°；（2）由（1）知，∠EAD=∠EAC-∠DAC=21∠BAC-（90°-∠C ）①把∠BAC=180°-∠B-∠C 代入①，整理得∠EAD=21∠C-21∠B ，∴2∠EAD=∠C-∠B ．23.证明： ∵∠ACB=90°， ∴∠1+∠3=90°，∵CD ⊥AB ，∴∠2+∠4=90°，又∵BE 平分∠ABC ，∴∠1=∠2，∴∠3=∠4，∵∠4=∠5，∴∠3=∠5，即∠CFE=∠CEF ．。

八年级数学上册11-1《与三角形有关的线段》基础同步练习题（含答案）1、如图所示，以BC为边的三角形共有（）．A. 1个B. 2个C. 3个D. 4个2、下列图形中，不是运用三角形的稳定性的是（）．A. 房屋顶支撑架B. 自行车三脚架C. 拉闸门D. 木门上钉一根木条3、以下是四位同学在钝角三角形ABC中画BC边上的高，其中画法正确的是()A. AB. BC. CD. D4、如图所示，已知BD是△ABC的中线，点E是BC的中点，则下列说法不正确的是（）．A. 点D是AC的中点B. AE是△ABC的中线C. AD=CD，BD=BCD. AD=CD，BE=EC5、下列各组数中，能作为一个三角形三边边长的是（）．A. 1，1，2B. 1，2，4C. 2，3，4D. 2，3，56、在△ABC中，AB=3，AC=5，第三边BC的取值范围是（）．A. 10<BC<13B. 4<BC<12C. 3<BC<8D. 2<BC<87、现有四根长度分别为2cm、4cm、6cm、8cm的木棒，从中任取三根，能组成三角形的个数为（）．A. 1B. 2C. 3D. 48、已知三角形的两边长分别为1和4，第三边长为整数，则该三角形的周长为（）．A. 7B. 8C. 9D. 109、已知△ABC的三边长分别为a，b，c，化简|a+b−c|−|b−a−c|的结果是．10、若等腰三角形的两边长分别为3和7，求该三角形的第三边长．11、等腰三角形的两边长分别为5cm和10cm，则此三角形的周长是（）．A. 15cmB. 20cmC. 25cmD. 20cm或25cm12、如图，在△ABC中，AB=8，AC=5，AD为中线，则△ABD与△ACD的周长之差为（）．A. 2B. 3C. 4D. 513、如图，在△ABC中，已知点D、E、F分别为BC、AD、CE的中点，且S△ABC=4cm2，则S△BEF=cm2．14、如图所示，顶点是A，B，C的三角形，记作，读作．其中，顶点A所对的边还可用表示；顶点B所对的边还可用表示；顶点C所对的边还可用表示．15、为了使一扇旧木门不变形，木工师傅在木门的背面加钉了一根木条，这样做的道理是．16、下列四个图形中，线段BE是△ABC的高的是（）．A.B.C.D.17、如图，在△ABC中，AD是高，AE是角平分线，AF是中线，则下列说法中错误的是（）．A. BF=CFB. ∠C+∠CAD=90°C. ∠BAF=∠CAFD. S△ABC=2S△ABF18、下列每组数分别是三根小木棒的长度，用它们能摆成三角形的是（）．A. 3cm，4cm，8cmB. 8cm，7cm，15cmC. 13cm，12cm，20cmD. 5cm，5cm，11cm19、已知一个三角形的两边长分别为8和2，则这个三角形的第三边长可能是（）．A. 4B. 6C. 8D. 1020、一个三角形的两边长分别为3和4，且第三边长为整数，这样的三角形的周长的最大值是（）．A. 11B. 12C. 13D. 1421、已知a、b、c是△ABC的三条边长，化简|a+b−c|+|b−a−c|的结果为（）．A. 2a+2bB. 2a+2b−2cC. 2b−2cD. 2a22、一个等腰三角形两边长分别为4cm和9cm，则它的周长为cm．23、一个等腰三角形的周长为30cm，一边长为6cm，求其他两边长．24、如图，AD是△ABC的中线，已知△ABD的周长为25cm，AB比AC长6cm，则△ACD的周长为（）．A. 19cmB. 22cmC. 25cmD. 31cm25、如图所示，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，且△ABC的面积是4cm2，则阴影部分面积等于（）．A. 2cm2B. 1cm2C. 0.25cm2D. 0.5cm226、如图，△ABC三边的中线AD、BE、CF的公共点为G，若S△ABC=12，则图中阴影部分的面积是．1 、【答案】 C;【解析】以BC为边的三角形有：△BCE、△BCA、△BCD．故选C．2 、【答案】 C;【解析】伸缩的的拉闸门是利用了四边形的不稳定性，A、B、D都是利用了三角形的稳定性，故选C．3 、【答案】 B;【解析】解：A、没有经过顶点A，不符合题意；B、高AD交BC的延长线于点D处，符合题意；C、垂足没有在BC上，不符合题意；D、AD不垂直于BC，不符合题意．故选B．4 、【答案】 C;【解析】5 、【答案】 C;【解析】 A选项 : 1+1=2，不满足三边关系，故错误．B选项 : 1+2<4，不满足三边关系，故错误．C选项 : 2+3>4，满足三边关系，故正确．D选项 : 2+3=5，不满足三边关系，故错误．6 、【答案】 D;【解析】根据三角形三边的不等关系可知，AC−AB<BC<AC+AB，即2<BC<8，故选D．7 、【答案】 A;【解析】能组成三角形的三根木棒的长度是4cm、6cm、8cm，只有一种结果．故选A．8 、【答案】 C;【解析】设第三边为x，根据三角形的三边关系，得：4−1<x<4+1，即3<x<5，∵x为整数，∴x的值为4，三角形的周长为1+4+4=9．故选C．9 、【答案】2b−2c;【解析】∵在△ABC根据两边之和大于第三边中，∴a+b>c，b<a+c，∵|b−a−c|=|b−(a+c)|，∴|a+b−c|−|b−a−c|=a+b−c−a−c+b=2b−2c．10 、【答案】7．;【解析】（1）若腰长为3，底边长为7，则三角形的三边长分别为3，3，7．∵3+3<7，∴此种情况不能围成三角形．（2）若腰长为7，底边长为3，则三角形的三边长分别为7，7，3．∵7+3>7，∴此种情况能围成三角形．综上知，该三角形的第三边长为7．11 、【答案】 C;【解析】5cm是腰长时，三角形的三边分别为5cm、5cm、10cm，∵5+5=10，∴不能组成三角形，10cm是腰长时，三角形的三边分别为5cm、10cm、10cm，能组成三角形，周长=5+10+10=25cm，综上所述，此三角形的周长是25cm．12 、【答案】 B;【解析】∵AD是△ABC的中线，∴BD=CD，∵△ABD周长=AB+AD+BD，△ACD周长=AC+CD+AD，∴△ABD周长−△ACD周长=(AB+BD+AD)−(AC+CD+AD)=AB−AC=8−5=3．故选B．13 、【答案】1;【解析】∵点E是AD的中点，∴S△BDE=12S△ABD，S△CDE=12S△ACD，∴S△BCE=12S△ABC=12×4=2cm2．∵点F是CE的中点，∴S阴影△BEF =12S△BCE=1cm2．14 、【答案】△ABC;三角形ABC;BC;a;AC;b;AB;c;【解析】15 、【答案】三角形具有稳定性;【解析】加上木条后，原来不稳定的四边形中具有了稳定的三角形，故这样做的数学道理是利用三角形的稳定性．16 、【答案】 D;【解析】A、B、C中线段BE不符合三角形高线的定义；D、线段BE是△ABC的高，即过点B作BE⊥AC，垂足在AC或其延长线上．故选D．17 、【答案】 C;【解析】∵AF是△ABC的中线，∴BF=CF，故A正确，∴S△ABF=S△ACF，∴S△ABC=2S△ABF，故D正确，∵AD是△ABC的高线，∴AD⊥BC，∴∠C+∠CAD=90°，故B正确，∵AE是△ABC的角平分线，∴∠BAE=∠CAE，故C错误，故选C．18 、【答案】 C;【解析】A选项，3+4<8，不能组成三角形，B选项，8+7=15，不能组成三角形，C选项，13+12>20，能够组成三角形，D选项，5+5<11，不能组成三角形．19 、【答案】 C;【解析】设第三边长为x，则8−2<x<2+8，6<x<10，故选：C．20 、【答案】 C;【解析】设第三边长为a，根据三角形的三边关系，得：4−3<a<3+4，即1<a<7，∵a为整数，∴a的最大整数值为6，则三角形的最大周长为3+4+6=13．故选：C．21 、【答案】 D;【解析】∵a、b、c为△ABC的三条边长，∴a+b−c>0，b−a−c<0，∴原式=a+b−c−(b−a−c)=a+b−c+c+a−b=2a．故选D．22 、【答案】22;【解析】当腰长是4cm，底边长是9cm时，不满足三角形的三边关系，因此舍去．当底边长是4cm，腰长是9cm时，能构成三角形，此时三角形的周长=4+9+9=22(cm)．故答案为22．23 、【答案】底边长是6cm的等腰三角形，其他两腰长为12cm．;【解析】因为长为6cm的边可能是腰，也可能是底边，所以需要分情况讨论．如果6cm长的边为底边，设腰长为xcm，则6+2x=30，解得x=12；如果6cm长的边为腰，设底边长为xcm，则2×6+x=30，解得x=18．因为6+6<18，不符合三角形两边之和大于第三边，所以不能围成腰长是6cm的等腰三角形．由以上讨论可知，可以围成底边长是6cm的等腰三角形，其他两腰长为12cm．24 、【答案】 A;【解析】∵AD是△ABC的中线，∴BD=CD，∵△ABD的周长为25cm，∴AB+BD+AD=25cm，∵AB比AC长6cm，∴AB=AC+6，∴AC+6+CD+AD=25cm，∴AC+CD+AD=19cm，即△ACD的周长为19cm．故选A．25 、【答案】 B;【解析】∵点F是CE的中点，∴△BEF的底是EF，△BEC的底是EC，EC，高相等；即EF=12S△BEC，∴S△BEF=12同理得，S△ABC，S△EBC=12S△ABC，且S△ABC=4cm2，∴S△BEF=14∴S△BEF=1cm2，即阴影部分的面积为1cm2．故选B．26 、【答案】4;【解析】设△AFG，△BFG，△BDG，△CDG，△CEG，△AEG的面积分别为S1，S2，S3，S4，S5，S6，根据中线平分三角形面积可得：S1=S2，S3=S4，S5=S6，S1+S2+S3=S4+S5+ S6①，S2+S3+S4=S1+S5+S6②由①−②可得S1=S4，同理可得S2=S5，所以S1=S2=S3=S4=S5=S6=2，故阴影部分的面积为4．。